AP Inter 1st Year Physics Important Questions Chapter 5 గమన నియమాలు

Students get through AP Inter 1st Year Physics Important Questions 5th Lesson గమన నియమాలు which are most likely to be asked in the exam.

AP Inter 1st Year Physics Important Questions 5th Lesson గమన నియమాలు

Very Short Answer Questions (అతిస్వల్ప సమాధాన ప్రశ్నలు)

ప్రశ్న 1.
జడత్వం అనగానేమి? జడత్వ కొలతను ఏది ఇస్తుంది?. [AP 19][IPE ’14][TS 17]
జవాబు:
జడత్వం :
ఒక వస్తువు దాని స్థితిలో మార్పును వ్యతిరేకించే ధర్మాన్ని జడత్వం అంటారు. వస్తువు యొక్క ద్రవ్యరాశి జడత్వానికి కొలమానంగా ఉంటుంది.

ప్రశ్న 2.
న్యూటన్ మూడవ గమన నియమము ప్రకారం, చర్యకు ప్రతిచర్య ఉంటే, గమనం అనేది ఏవిధంగా సాధ్యమవుతుంది?
జవాబు:
బలాల జంట ఒకే వస్తువుపై పనిచేయవు. అందువలన ఆ రెండు బలాలు రద్దుకావు. కావున గమనం సాధ్యమగును.

ప్రశ్న 3.
ఒక తుపాకీ నుంచి బుల్లెట్ను పేల్చినపుడు, తుపాకీని వెనకకు నెట్టివేసినట్లు అనిపిస్తుంది. వివరించండి. [AP 15]
జవాబు:
ద్రవ్యవేగ నిత్యత్వ నియమం ప్రకారం తుపాకీ నుంచి బుల్లెట్ను పేల్చినపుడు, తుపాకీ ద్రవ్యవేగం బుల్లెట్ ద్రవ్యవేగమునకు పరిమాణంలో సమానంగానూ దిశలో వ్యతిరేకంగా ఉంటుంది. బుల్లెట్ ముందుకు పోతుంటే తుపాకీ వెనుకకు వస్తుంది. ఈ చలనాన్ని తుపాకీ ప్రత్యావర్తకం అంటారు.

ప్రశ్న 4.
ఒకే గుళ్ళను ఉపయోగించినా బరువుగా ఉన్న రైఫిల్ తేలికైన రైఫిల్ కంటే తక్కువ వేగంతో వెనుకకు చలిస్తుంది. ఎందువల్ల? [TS 17] [Imp.Q]
జవాబు:
రైఫిల్ ప్రత్యావర్తనం V = \(\frac{mu}{M}\)
రైఫిల్ ద్రవ్యరాశి (M) అధికము. M విలువ హారములో ఉన్నది కావున రైఫిల్ ప్రత్యావర్తనం తక్కువ.

ప్రశ్న 5.
విరామస్థితిలో ఉన్న ఒక బాంబు రెండు ముక్కలుగా పేలితే దాని ముక్కలు వ్యతిరేకదిశలో చలిస్తాయి. వివరించండి. [TS 15, 22]
జవాబు:
బాంబు నిశ్చల స్థితిలో ఉన్నపుడు దాని రేఖీయ ద్రవ్యవేగం శూన్యం. అంతర్గత బలాల వలన బాంబు పేలి రెండు ముక్కలయినపుడు, రేఖీయ ద్రవ్యవేగ నిత్యత్వ నియమం ప్రకారం ఆ రెండు ముక్కల మొత్తము ద్రవ్యవేగము శూన్యమవ్వాలి. అందువలన ఆ రెండు ముక్కలకు సమానం మరియు వ్యతిరేకమయిన ద్రవ్యవేగాలు ఉంటాయి. కావున అవి ప్రయాణం చేసే దిశలు వ్యతిరేకంగా ఉంటాయి.

ప్రశ్న 6.
బలాన్ని నిర్వచించండి. ప్రకృతిలోని ప్రాథమిక బలాలను పేర్కొనండి. [Imp.Q]
జవాబు:
బలం :
ఒక వస్తువు స్థితిని మార్చేది లేదా మార్చడానికి ప్రయత్నించే భౌతికరాశిని బలం అంటారు.

ప్రకృతిలో ప్రాధమిక బలాలు :
గురుత్వబలం, విద్యుత్ అయస్కాంతబలం, కేంద్రక బలాలు. (ప్రబల కేంద్రక బలం మరియు దుర్బల కేంద్రక బలం)

ప్రశ్న 7.
ఘర్షణ గుణకం విలువ ఒకటికంటే ఎక్కువ ఉంటుందా? [TS 18]
జవాబు:
సాధారణంగా ఘర్షణ గుణకం 1 కన్నా తక్కువ ఉంటుంది. అయితే స్పృశించే రెండు తలాలను వాటి అణు దూరాల వరకు వేరుచేస్తే అణువుల మధ్య ఆకర్షణ బలాలు పెరిగి ఘర్షణ గుణకం విలువ ఒకటికంటే ఎక్కువ అయ్యే అవకాశం ఉంటుంది. కానీ సాధారణంగా ఇది సాధ్యం కాదు.

ప్రశ్న 8.
గాలి నిండిన టైర్లను కలిగి ఉన్న కారు కంటే గాలి లేని టైర్లు ఉన్న కారు తొందరగా ఆగుతుంది. ఎందుకు? [AP 20]
జవాబు:
స్పర్శలో ఉన్న తలాల రూపం మారితే దొర్లుడు ఘర్షణ పెరుగుతుంది. గాలి ఉన్న టైరు కన్నా గాలి లేని టైరుకు విరూపం ఎక్కువ. అందువల్ల ఘర్షణ పెరిగి గాలిలేని కారు టైరు త్వరగా ఆగిపోతుంది.

ప్రశ్న 9.
గుర్రం చలనంలో ఉన్నప్పటి కంటే, అది బయలుదేరుట ప్రారంభించే సమయంలో ఎక్కువ బలాన్ని ఎందుకు ఉపయోగిస్తుంది? [AP 22][AP, TS 16,18]
జవాబు:
గుర్రంబండి నిశ్చలస్థితిలో ఉన్నప్పుడు, గమనంలోకి తేవడానికి గరిష్ఠ స్థితిక ఘర్షణ బలాన్ని అధిగమించే ఘర్షణ బలం పని చేయాలి. బండి గమనంలోకి వచ్చిన తర్వాత ఘర్షణబలం తగ్గుతుంది. అందువలన గమనానికి ముందు గుర్రంబండిపై ఎక్కువ బలం ప్రయోగించాలి.

ప్రశ్న 10.
వస్తువు భారాన్ని రెట్టింపు చేస్తే ఘర్షణ గుణకం ఏమవుతుంది.? [TS 19, 22][AP 16, 19]
జవాబు:
ఘర్షణ గుణకం వస్తువు భారంపై ఆధారపడి ఉండదు. ఘర్షణ గుణకం విలువ ఎప్పుడూ మారదు.

Short Answer Questions (స్వల్ప సమాధాన ప్రశ్నలు)

ప్రశ్న 1.
0.1 కి.గ్రా ద్రవ్యరాశి గల రాయిని నిలువుగా పైకి విసిరారు. క్రింది సందర్భాలలో రాయిపై పనిచేసే నికర బలం పరిమాణం దిశను తెలపండి. (a) నిలువుగా పైకి ప్రయాణిస్తున్నప్పుడు (b) క్రిందికి ప్రయాణిస్తున్నప్పుడు (c) గరిష్ట ఎత్తు వద్ద (ఎక్కడైతే క్షణం పాటు రాయి విరామ స్థితికి వస్తుందో)
జవాబు:
పై మూడు సందర్భములలోనూ రాయిపై పనిచేయు ఏకైక బలము గురుత్వాకర్షణ బలం. రాయి భూమికి సమీప ఎత్తులో ఉన్నంత వరకు రాయిపై పనిచేయు గురుత్వాకర్షణ బలం పరిమాణంలోనూ, దిశలోను స్థిరముగా ఉండును. రాయి పై పని చేయు గురుత్వాకర్షణ బలం m = 0.1kg, g = 9.8 మీసె^-2.
∴ F = mg= 0.1 × 9.8 = 0.98 N ఈ బలం ఎల్లప్పుడు క్రింది దిశలో పని చేయును.

ప్రశ్న 2.
ద్రవ్యవేగం, ప్రచోదనాలను నిర్వచించండి? రేఖీయ ద్రవ్యవేగ నిత్యత్వ నియమాన్ని నిర్వచించి, వివరించండి. ఉదాహరణలు ఇవ్వండి. [Imp.Q][TS 15,18][AP 20]
జవాబు:
ద్రవ్యవేగము(p) :
ఒక వస్తువు యొక్క ద్రవ్యరాశి మరియు వేగముల లబ్దాన్ని ద్రవ్యవేగము అంటారు.

ప్రచోదనం(J) :
బలం మరియు కాలముల లబ్ధాన్ని ప్రచోదనంగా నిర్వచిస్తారు. లేదా ఒక వస్తువు మీద కొంత బలం ప్రయోగించినపుడు దాని రేఖీయ ద్రవ్యవేగంలో సంభవించే మార్పును ప్రచోదనం అంటారు.
ప్రచోదనం = బలం × కాలం

రేఖీయ ద్రవ్య వేగ నిత్యత్వ నిమయం :
అన్యోన్య చర్యగల కణాలు కలిగిఉన్న ఒక వియుక్త వ్యవస్థపై ‘ఫలిత బాహ్యబలం’ పనిచేయనపుడు, ఆ వ్యవస్థయొక్క మొత్తం ద్రవ్యవేగం స్థిరంగా ఉంటుంది.

అభిఘాతం ముందు మొత్తం ద్రవ్యవేగం = అభిఘాతం తరువాత మొత్తం ద్రవ్యవేగం.

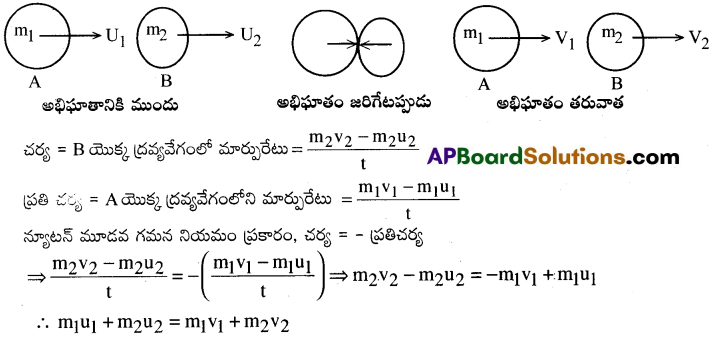
కావున, అభిఘాతం ముందు ద్రవ్యవేగం = అభిఘాతం తర్వాత మొత్తం ద్రవ్యవేగం

ఉదా -1 : విస్ఫోటనం చెందే బాంబు :
నిశ్చల స్థితిలో ఉన్న బాంబు విస్ఫోటనం చెంది రెండు ముక్కలుగా విడిపోతే ద్రవ్యవేగ నిత్యత్వ నియమం ప్రకారం,
విస్ఫోటనానికి ముందు మొత్తం ద్రవ్యవేగం = విస్ఫోటనం తర్వాత మొత్తం ద్రవ్యవేగం
⇒ 0= m₁v₁ + m₂v₂ → m₁v₁ = -m₂v₂
అనగా విస్ఫోటనం చెందిన రెండు ముక్కల యొక్క ద్రవ్యవేగం అభిఘాతానికి ముందు, తర్వాత సమానము మరియు వ్యతిరేకం
ఉదా -2 : రాకెట్ మరియు జెట్ విమానంల ‘చలనం’ ద్రవ్యవేగ నిత్యత్వ నియమాన్ని పాటించును.

ప్రశ్న 3.
మోటారు సైకిళ్లు, కార్లకు షాక్ అబ్జార్బర్లను ఎందుకు ఉపయోగిస్తారు? [AP 15]
జవాబు:
గతుకుల రోడ్లపై వాహనాలు ప్రయాణించేటపుడు షాక్ అబ్జార్బర్ల వలన ప్రచోదనకాలం పెరుగుతుంది. ఫలితంగా ప్రచోదన బలం తగ్గుతుంది. అందువల్ల ప్రయాణికుడు సౌకర్యమైన ప్రయాణాన్ని పొందుతాడు.

ప్రశ్న 4.
సీమాంత స్థితిక ఘర్షణ, గతిక ఘర్షణ మరియు దొర్లుడు ఘర్షణలను వివరించండి. [Imp.Q]
జవాబు:
1) సీమాంత స్థితిక ఘర్షణ (fms) :
నిశ్చల స్థితిలో ఉన్న వస్తువు కదలడానికి సిద్ధంగా ఉన్నప్పుడు వాటి తాకే తలాల మధ్య పని చేసే గరిష్ట స్థితిక ఘర్షణ బలాన్ని సీమాంత స్థితిక ఘర్షణ అంటారు.

2) గతిక (లేదా) జారుడు ఘర్షణ (f) :
తలంపై జారుతున్న వస్తు గమనాన్ని నిరోధించే బలాన్ని గతిక (లేదా) జారుడు ఘర్షణ అని అంటారు.

3) దొర్లుడు ఘర్షణ (fr) :
ఒక తలంపై దొర్లుతున్న వస్తువు గమనాన్ని నిరోధించే బలాన్ని దొర్లుడు ఘర్షణ అంటారు.

ప్రశ్న 5.
ఘర్షణ వలన కలిగే లాభాలు, నష్టాలను వివరించండి. [*Imp.Q][AP 15,19][TS 15,17,22]
జవాబు:
ఉపయోగాలు :

1. పాదాలకు, భూమికి మధ్య ఘర్షణ లేకపోతే మనం భూమిపై నడవలేం.
2. బ్రేకులు ఉపయోగించి వాహనాలను రోడ్లపై ఆపడానికి ఘర్షణ బలమే కారణం.
3. టేబుల్పై ఉన్న బుక్ను పట్టుకోగలగటానికి గల కారణం చేతికి, బుక్కి మధ్య గల ఘర్షణ బలం.
4. యంత్రానికి అమర్చిన బెల్టుద్వారా యాంత్రికశక్తి యొక్క ప్రసరణ ఘర్షణబలం వల్లే సాధ్యమవుతుంది.

నష్టాలు :

1. ఘర్షణ వల్ల యంత్రభాగాలలో శక్తి నష్టం జరుగుతుంది.
2. ఘర్షణ వల్ల యంత్రభాగాలలోని వివిధ భాగాలు అరిగిపోవడం, కోతకు గురికావడం జరుగుతుంది. దీనివల్ల
   జీవితకాలం తగ్గుతుంది.

ప్రశ్న 6.
ఘర్షణను తగ్గించే పద్ధతులను తెలపండి. [AP 18,22] [IPE ‘14,14][TS 16,17,19]
జవాబు:
1) పాలిష్ చేయడం :
తలాలను పాలిష్ చేయడం వల్ల ఆ తలాల మధ్య ఘర్షణను తగ్గించవచ్చు.

2) స్నేహకాలను వాడటం :
ఘర్షణను తగ్గించడానికి స్పర్శలో గల రెండు తలాల మధ్య స్నేహకాలను ఉపయోగిస్తారు.

3) బాల్ బేరింగులు ఉపయోగించడం :
సైకిళ్ళు, ద్విచక్ర వాహనాలు, మోటారు కార్లు, డైనమో లాంటి స్వేచ్ఛగా తిరిగే వాహన చక్రాల నడిమి భాగాలకు బాల్ బేరింగులను ఘర్షణ తగ్గించడానికి ఉపయోగిస్తారు.

4) ధారావాహికాకారం :
మోటారు వాహనాలు, విమానాలు మొదలైన వాటిని ఘర్షణను తగ్గించడానికి ప్రత్యేకమైన ఆకారంలో రూపొందిస్తారు. దీనినే ధారావాహికాకారం అంటారు.

ప్రశ్న 7.
దొర్లుడు ఘర్షణ నియమములను వ్రాయండి. [Imp.Q] [TS 20,22]
జవాబు:
దొర్లుడు ఘర్షణ (f_r) :
ఒక తలంపై దొర్లుతున్న వస్తువు గమనాన్ని నిరోధించే బలాన్ని దొర్లుడు ఘర్షణ అంటారు.

దొర్లుడు ఘర్షణ నియమాలు :

1. స్పర్శా వైశాల్యం తక్కువగా ఉంటే దొర్లుడు ఘర్షణ కూడా తక్కువగా ఉంటుంది.
2. దొర్లుతున్న వస్తువు వ్యాసార్థం ఎక్కువగా ఉంటే, దొర్లుడు ఘర్షణ తక్కువగా ఉంటుంది.
3. దొర్లుడు ఘర్షణ, అభిలంబ ప్రతిచర్యకు అనులోమానుపాతంలో ఉంటుంది. అనగా (f_r ∝ N)
   ⇒ f_r ∝ N ⇒ f_r = µ_rN. ఇక్కడ µ_r అనునది దొర్లుడు ఘర్షణ గుణకం.

ప్రశ్న 8.
లాన్ రోలర్ను నెట్టడం కంటే లాగడం తేలిక. ఎందుకు? [Imp.Q]
జవాబు:
క్షితిజ సమాంతరంతో ‘θ’ కోణం చేస్తూ ‘F’ బలం ఉపయోగించి లాన్ రోలర్ను లాగారనుకోండి. F ను పరస్పరం లంబాంశాలుగా విభజిస్తే అవి Fcosθ మరియు Fsinθ అగును.

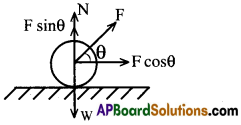
ఊర్థ్వదిశలో మొత్తం బలం = అధోదిశలో మొత్తం బలం
N + Fsinθ = W ⇒ N = W – Fsinθ
కాని ఘర్షణ బలం f = µN
⇒ f = μ(W – Fsinθ) ——–(1)
లాన్ రోలరు క్షితిజ సమాంతరంతో ‘θ’ కోణం చేస్తున్న ‘F’ బలం తో నెట్టినారనుకోండి.
ఇక్కడ బలం ‘F’ ను పరస్పరం లంబాంశాలుగా విభజిస్తే అవి Fcosθ మరియు Fsinθ.

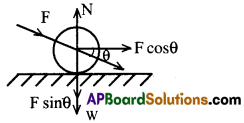
ఊర్ధ్వదిశలో మొత్తం బలం = అధోదిశలో మొత్తం బలం
N = W + Fsinθ
ఘర్షణ బలం f = µN
⇒ f = µ(W + Fsinθ) ——–(2)
(1), (2) సమీకరణాలను పోల్చగా లాన్ రోలర్ను నెట్టుట కంటే లాగడం సులభం అని తెలియుచున్నది.

Long Answer Questions (దీర్ఘ సమాధాన ప్రశ్నలు)

ప్రశ్న 1.
న్యూటన్ రెండవ గమన నియమాన్ని తెలపిండి. దాని నుంచి గమన సమీకరణం F = ma ను రాబట్టండి. ఒక వస్తువు వృత్తపథంలో ఎప్పుడూ సమవడితో చలిస్తూ ఉంటే దాని మీద బలం పనిచేస్తుందా? [TS 18][Mar 13, May 13][AP 16,17,19]
జవాబు:
న్యూటన్ రెండవ గమన నియమం : “ఒక వస్తువు యొక్క ద్రవ్యవేగంలోని మార్పు రేటు ఆ వస్తువుపై ప్రయోగించిన బాహ్యబలానికి అనులోమానుపాతంలో ఉండి, బాహ్యబలం పనిచేసే దిశలో ఉంటుంది”.
F = ma అని చూపుట:
m = వస్తువు యొక్క ద్రవ్యరాశి,
v = వస్తువు యొక్క వేగం
ఒక వస్తువు ద్రవ్యరాశి ‘m’ మరియు వేగం’v’ ల లబ్దమే ద్రవ్యవేగం ‘p’. ∴ p = mv
F = వస్తువుపై పనిచేసే బాహ్యబలం
dp అనునది dt కాలంలో వస్తువు యొక్క ద్రవ్యవేగంలోని మార్పు అయితే.

ఏకాంక బలం వద్ద m = 1, a = 1, f = 1 అయితే k = 1 అగును. అపుడు పై సమీకరణము F = ma అగును.

వృత్తాకార మార్గంలో స్థిర వడితో చలించే వస్తువుపై పనిచేసే బలం :
వృత్తాకార మార్గంలో స్థిర వడితో ప్రయాణించే వస్తువుకు వేగం ఉంటుంది. ఈ వేగం యొక్క దిశ ఆ బిందువు వద్ద గీసిన స్పర్శరేఖ వెంబడి పనిచేస్తుంది. అందువల్ల వేగ దిశ క్షణక్షణానికి మారుతుంది. కావున ఆ వస్తువుపై త్వరణము తద్వారా బలము పనిచేస్తున్నట్లే.

ప్రశ్న 2.
ఘర్షణ కోణం, విశ్రామ కోణాలను నిర్వచించండి. గరుకు వాలు తలం విషయంలో ఘర్షణ కోణం, విశ్రామ కోణానికి సమానమని చూపండి.
గరుకు క్షితిజ సమాంతర తలముపై 4 కి.గ్రా ద్రవ్యరాశి ఉన్న ఒక చెక్క దిమ్మె విరామస్థితిలో కలదు. దిమ్మెపై 30N క్షితిజ సమాంతర బలాన్ని ప్రయోగిస్తే అది కదలడానికి సిద్ధం అయ్యింది. g = 10 ms^-2 అయితే, దిమ్మెపై ఆ తలం ప్రయోగించే మొత్తం స్పర్శా బలాన్ని కనుక్కోండి.
జవాబు:
ఘర్షణ కోణం (θ):
అభిలంబ ప్రతిచర్య N మరియు సీమాంతర ఘర్షణల ఫలితబలం \(\overline{\mathrm{f_{ms}}}\)ms, అభిలంబ ప్రతిచర్యతో చేసే కోణాన్ని ఘర్షణ కోణం అంటారు.

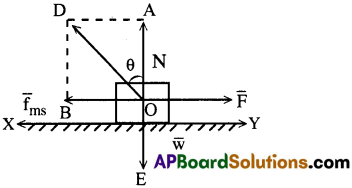
పటము నుండి tan θ = \(\frac{A D}{O A}=\frac{f_{m s}}{N}\) = µ_s ………. (1)

విశ్రామ కోణం(Φ) :
క్షితిజ సమాంతరంతో వాలుతలం చేస్తున్న కోణం యొక్క ఏ విలువకైతే వస్తువు జారడానికి సిద్ధంగా ఉంటుందో ఆ కోణాన్ని విశ్రామ కోణం (Φ) అంటారు.

గురుకు వాలు తలం విషయంలో ఘర్షణకొణం, విశ్రామ కోణము నకు సమానమని చూపుట.

1. క్షితిజ సమాంతరముతో Φ కోణం చేయుచున్న OA అను వాలు తలముపై w భారము గల వస్తువు ఉన్నదనుకొనుము. వస్తువు భారం దాని గరిమనాభి బిందువు వద్ద నుండి నిట్ట నిలువుగా క్రింది దిశలో పని చేయుచుండును.
2. వాలు తలము కోణమును క్రమ క్రమముగా పెంచుచున్నపుడు, ఒకానొక కోణం వద్ద వస్తువు జారుట ఆరంభించును. ఆ కోణమును విశ్రామ కోణం అని అంటారు. ఆ కోణం Φ అనుకొనుము. Φ విలువ స్పృశించుకొను రెండు తలముల స్వభావము పై ఆధారపడి ఉండును.
3. వస్తువు భారము W ను రెండు అంశలుగా విభజించినపుడు (a) వాలు తలమునకు లంబ దిశలో wcos Φ మరియు వాలు తలమునకు సమాంతరముగా wsinΦ అగును. wcosΦ విలువ లంబ ప్రతీకార చర్య N కు తుల్యమగును మరియు wsinΦ విలువ సీమాంతర స్థితిక ఘర్షణకు సమానమగును.

వస్తువు జారుటకు సిద్ధముగా ఉన్నది కనుక wsinΦ = f_ms మరియు wcosΦ = N

∴ tanθ = tanΦ ⇒ θ = Φ విశ్రామ కోణం = ఘర్షణ కోణం

లెక్క:
ఘర్షణ బలము, అభిలంబ చర్యలు స్పర్శ బలములు. అవి రెండు పరస్పరము లంబముగా ఉన్నవి. కావున వాని
ఫలిత బలమే మొత్తము స్పర్శ బలము అగును.
ఇచ్చినది m = 4kg and g = 10ms^-2.

Solved Problems (సాధించిన సమస్యలు)

ప్రశ్న 1.
అంతరాళములో నక్షత్రముల మద్య ఒక చిన్న విమాన నౌక 100 మీసె^-2. సమత్వరణంతో ప్రయాణించుచున్నది. అనుకోనట్టుగా దానిలోని ఒక వ్యోమగామి అంతరిక్ష నౌక నుండి బయటకు పడి పోయెను. బయట పడిన మరుక్షణం ఆ వ్యోమగామి త్వరణం ఎంత? అంతరిక్షనౌకకు సమీపములో నక్షత్రములు గాని మరి ఏ ఇతర గ్రహములు గాని అతనిపై గురుత్వాకర్షణ బలములను ప్రయోగించుట లేదు అని అనుకొనుము.
సాధన:
అతని పై గురుత్వాకర్షణ బలములు ఏవియు పని చేయుట లేదు. కనుక అంతరిక్ష నౌక నుండి బయటపడిన మరుక్షణం నుండి అతని పై పనిచేయు బలములు శూన్యము. అందువలన న్యూటన్ మొదటి గమన నియమం ప్రకారం అతని త్వరణం కూడ శూన్యము.

ప్రశ్న 2.
0.04 కి.గ్రా. ద్రవ్యరాశి గల బుల్లెట్ 90 మీ/సె. వేగంతో ఒక చెక్క దిమ్మెలోనికి ప్రవేశించి 60 సెం.మీ. దూరం ప్రయాణించిన తరువాత ఆగిపోయినది. అయిన చెక్క దిమ్మె బుల్లెట్ పై ప్రయోగించిన సగటు నిరోధ బలం ఎంత?
సాధన:
బుల్లెట్ ద్రవ్యరాశి (m) = 0.04 కి.గ్రా, బుల్లెట్ తొలివేగం (u) = 90 మీ/సె, బుల్లెట్ తుదివేగం (v) = 0 ప్రయాణించిన దూరం (s) = 60 సెం.మీ = 0.6 మీ, బుల్లెట్ ఋణత్వరణం =?

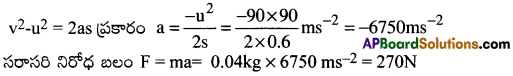
ప్రశ్న 3.
m ద్రవ్యరాశి గల ఒక కణము యొక్క చలన సమీకరణం y = ut + \(\frac{1}{2}\)gt² అయిన కణము పై పని చేయుచున్న బలం ఎంత?
సాధన:

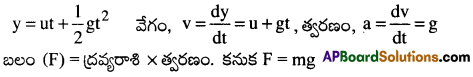
ప్రశ్న 4.
ఒక క్రికెట్ బంతి ద్రవ్యరాశి 0.15 కి.గ్రా. ఒక బౌలర్ ఆ బంతిని 12 మీ/సె. వేగంతో ఒక బ్యాట్స్మెన్ వైపు విసరగా అతడు బంతి వేగము మారకుండా దిశ మాత్రము వ్యతిరేకము అగునట్లు కొట్టెను. అయిన ఆ బంతి పై ప్రచోదనము ఎంత? [AP 17][TS 20]
సాధన:
ప్రచోదనము = ద్రవ్యవేగములోని మార్పు, బంతి ద్రవ్యరాశి m = 0.15 కి.గ్రా, బంతి తొలి వేగము u = 12 మీ/సె
బంతి తుది వేగము v = – 12 మీ/సె (దిశ వ్యతిరేకమయినది కనుక)

బంతి ద్రవ్యవేగములోని మార్పు = తుది ద్రవ్యవేగము – తొలి ద్రవ్యవేగము =(0.15 × 12) – (-0.15 × 12) = 3.6 Ns
ప్రచోదనము = ద్రవ్యవేగములోని మార్పు = 3.6 న్యూ. సె

ప్రశ్న 5.
ఒక రైలు పెట్టె లోపల నేలపై ఒక పెట్టె విరామస్థితిలో ఉన్నది. నేలకు, పెట్టెకు మధ్య ఘర్షణ గుణకం 0.15 అయిన రైలు గరిష్టముగా ఎంత త్వరణముతో వెళ్ళు వరకు పెట్టె విరామ స్థితిలో ఉండును.
సాధన:
రైలు పెట్టెతో పోల్చినపుడు పెట్టె విరామ స్థితిలో ఉన్నది. అనగా రైలు త్వరణమునకు సమానముగా పెట్టె త్వరణము ఉండవలయును. ఈ త్వరణమును పెట్టెకు, రైలు నేలకు మధ్యగల స్థితిక ఘర్షణ బలము సమకూర్చును. పెట్టె ద్రవ్యరాశి m, రైలు త్వరణము a అయితే
∴ a_max = µ_sg = 0.15 × 10 మీసె^-2 = 1.5 మీసె^-2

Exercise Problems

ప్రశ్న 1.
కాలము t తో ఒక కణము ద్రవ్యవేగము p మారు విధానము p = a + bt తో సూచించిన కణము పై పనిచేయు బలం ఎంత? a, b లు ధన స్థిరాంకములు.
సాధన:
ద్రవ్యవేగము p = a + bt, బలం, F = ?
బలం = ద్రవ్యవేగములోని మార్పు రేటు
F = \(\frac{dp}{dt}=\frac{d}{dt}\)(a + bt) = b
∴ కణము పై బలం = b

ప్రశ్న 2.
10 కి.గ్రా ద్రవ్యరాశి గల వస్తువు వేగము ఎంత కాలములో 2 మీ/సె. మారును? వస్తువు పై పని చేయుచున్న బలం 5 న్యూ. [TS 16]
సాధన:
వస్తువు పై బలం, F = 5 న్యూ
వస్తువు ద్రవ్యరాశి, m = 10 కి.గ్రా
వస్తువు వేగములోని మార్పు, v – u = 2 మీ సె^-1

ప్రశ్న 3.
m ద్రవ్యరాశి గల బంతి నిట్ట నిలువుగా పైకి విసిరినపుడు అది చేరిన గరిష్ట ఎత్తు h అయిన బంతి గమన సమయములో గురుత్వాకర్షణ బలము వలన పొందిన ప్రచోదనము ఎంత? గురుత్వత్వరణం g అనుకొనుము.
సాధన:

ప్రశ్న 4.
3కి.గ్రా. ద్రవ్యరాశి గల వస్తువు పై ఒక స్థిర బలము పని చేసి దాని వేగమును 25 సెకనులలో 2 మీ/సె. నుండి 3.5 మీ/సె. కు మార్చినది. వస్తువు చలన దిశలో మార్పులేదు. అయిన బలము పరిమాణము ఎంత మరియు దిశ ఏది?
సాధన:
వస్తువు ద్రవ్యరాశి, m = 3 కి.గ్రా
తొలి వేగం, u = 2 మీసె^-1
తుది వేగం, v = 3.5 మీసె^-1
కాలం t = 25 సె
బలం F = ?

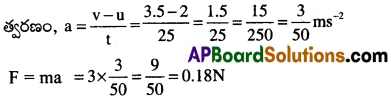
వస్తువు వేగము పెరిగినది కనుక వస్తువు చలన దిశలోనే బలము ప్రయోగించబడినది.

ప్రశ్న 5.
ఒక లిఫ్ట్ గురుత్వత్వరణంలో 1/3 వ వంతు ఏకరీతి త్వరణంతో పైకి చలిస్తున్నప్పుడు లిఫ్ట్ లో ఉన్న వ్యక్తి దృశ్యభారం W. అదే లిఫ్ట్ గురుత్వత్వరణములో 1/2 వ వంతు ఏకరీతి త్వరణంతో కిందికి చలిస్తున్నప్పుడు అతడి దృశ్యభారం ఎంత?
సాధన:
వ్యక్తి నిజ భారము mg అనుకొనుము. లిఫ్ట్ పై దిశలో ‘a’ త్వరణంతో వెళ్ళుచున్నపుడు వ్యక్తి దృశ్య భారము mg + ma అగును.

ప్రశ్న 6.
పై కప్పులేని ఒక ట్రక్ వెనుక భాగమున 200 కి.గ్రా. ద్రవ్యరాశి గల వస్తువు ఉన్నది. ట్రక్ 1.5 మీ/సె². త్వరణముతో ప్రయాణించుచున్నది. వస్తువు జారకుండ ఉండుటకు వస్తువునకు, ట్రక్ నేలకు మధ్య ఉండవలసిన కనిష్ట ఘర్షణ గుణకం ఎంత?
సాధన:
వస్తువునకు ట్రక్ నకు ఉన్న త్వరణము ఉన్నపుడు మాత్రమే వస్తువు జారకుండ ఉండును. ఈ త్వరణమునకు కావలసిన బలమును వస్తువునకు, ట్రక్ నేలకు మధ్యగల ఘర్షణ బలము సమకూర్చును.
కావున F = ma = 200 × 1.5 = 300 N
∴ ఘర్షణ గుణకం (f) = 300 = µN = 300 ⇒ µmg = 300

ప్రశ్న 7.
నేల నుండి 40 మీటర్ల ఎత్తులో విరామ స్థితిలో ఉన్న ఒక బాంబు అకస్మాత్తుగా రెండు సమానమైన ముక్కలుగా పేలి పోయినది. ఒక ముక్క నిట్టనిలువుగా క్రింది దిశలో 10 మీ/సె. వేగంతో పడిపోవుట ఆరంభించినది.
g = 10 మీ/సె² అయిన బాంబు ప్రేలిన 2 సెకనుల తరువాత రెండు ముక్కల మధ్య దూరం ఎంత?
సాధన:
విరామ స్థితిలో ఉన్న బాంబు రెండు సమానమైన ముక్కలుగా విడిపోయి, ఒక ముక్క 10 మీ/సె వేగంతో క్రింది దిశలో ప్రయాణించుట ఆరంభించినది. కావున ద్రవ్యవేగ నిత్యత్వ నియమం ప్రకారం రెండవ ముక్క నిట్టనిలువుగా పై దిశలో 10మీ/సె వేగంతో ప్రయాణించుట ఆరంభించును.
పై దిశలో ప్రయాణించు ముక్కకు, ఆరోహణకాలం (t_a) = \(\frac{u}{g}=\frac{10}{10}\) = 1 sec

అనగా 1 సెకనులో అది గరిష్ట ఎత్తును చేరి, ఇంకొక 1 సెకనులో అది మరల బాంబు పేలిన స్థానమునకు వచ్చును. క్రింది దిశలో ప్రయాణించు చున్న ముక్కకు తొలి వేగం (u) = 10 మీసె^-1
గురుత్వత్వరణం (a) = g = 10 మీసె^-2, కాలం (t) = 2 సె, ప్రయాణించు దూరం (s) = ?

s = ut + \(\frac{1}{2}\)at² ⇒ s =10 × 2 + \(\frac{1}{2}\) × 10 × 4 = 20 + 20 = 40m
అనగా రెండవ ముక్క నేలను తాకును. అందువలన 2 సెకనుల తరువాత రెండు ముక్కల మధ్య దూరం = మొదట్లో బాంబు నేల నుండి ఉన్న ఎత్తు = 40 మీ.

ప్రశ్న 8.
ఘర్షణ లేని ఒక స్థిర కప్పీ గాడి ద్వారా వెళ్ళుచున్న ఒక తేలికైన త్రాడు ఒక చివర 4 కి.గ్రా. ద్రవ్యరాశి గల వస్తువు, రెండవ చివర 3 కి.గ్రా. ద్రవ్యరాశి గల వస్తువు ఉన్నవి. ఇంకొక తేలికైన త్రాడు సహాయముతో 3కి.గ్రా. వస్తువునకు ఇంకొక 3 కి.గ్రా. వస్తువును పటములో చూపినట్లు కలిపారు. ఈ వ్యవస్థను విరామస్థితి నుండి వదిలిన ఉమ్మడి త్వరణమును కనుక్కోండి. (g = 10ms²)

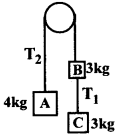
సాధన:
వ్యవస్థను విరామస్థితి నుండి వదిలినపుడు A పై దిశలో, B మరియు C క్రింది దిశలో ఒక ఉమ్మడి త్వరణంతో పయనించును. ఆ ఉమ్మడి త్వరణం ” అనుకొనుము. A,B లు ఒకే త్రాడు చివరల ఉన్నవి కనుక వానిపై దిశలో పనిచేయు తాడు తన్యత సమానముగా ఉండును. A యొక్క త్వరణం పై దిశలో a కనుక:

ప్రశ్న 9.
ఒక గరుకు వాలు తలము క్షితిజ సమాంతర దిశలో 30° కోణము చేయుచున్నది. ఆ వాలు తలము పై 2 కి.గ్రా. ద్రవ్యరాశి గల వస్తువు ఉన్నది. వస్తువు, వాలు తలముల మధ్య ఘర్షణ గుణకం √3/2.
(a) వస్తువు వాలు తలము పై క్రింది దిశలో స్థిర వేగముతో పయనించుటకు వసువు పై ప్రయోగించవలసిన బలం ఎంత?
(b) వస్తువు వాలు తలము పై దిశలో స్థిర వేగముతో పయనించుటకు వస్తువు పై ప్రయోగించవలసిన బలం ఎంత?
సాధన:

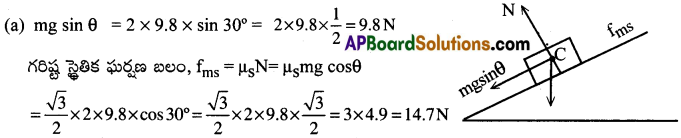
వస్తువు వాలు తలము పై క్రింది వైపునకు స్థిర వేగముతో ప్రయాణించుటకు ప్రయోగించ వలసిన బలం F₁ అయితే
F₁ + mg sin θ = f_ms
⇒ F₁ + 9.8 = 14.7
⇒ F₁ = 4.9 N

(b) వస్తువు వాలు తలము పై పైకి జరుగుచున్నపుడు mg sinθ ఘర్షణబలం క్రింది దిశలో ఉండును. కాబట్టి వస్తువును స్థిరవేగముతో పైకి జరుపుటకు ప్రయోగించవలసిన బలం f_ms అయితే
F = mg sinθ + f_ms = 9.8 + 14.7 = 24.5 N

ప్రశ్న 10.
y = x²/20 సమీకరణముతో సూచించబడు పరావలయ ఆకారములో ఒక చెక్క ఉన్నది. దానిపై ఒక చెక్క దిమ్మె ఉన్నది. ఆ రెండింటికి మధ్య ఘర్షణ గుణకం µ_s = 0.5, అయిన నేల నుండి ఎంత ఎత్తులో ఉంచినంత వరకు చెక్క దిమ్మె పరావలయ తలము పై జారకుండ ఉండును?
సాధన:
లెక్క ప్రకారం µ_s = 0.5

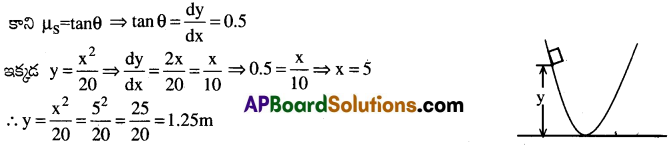
ప్రశ్న 11.
ఒక క్షితిజ సమాంతర బల్ల పై 2 కి.గ్రా. ద్రవ్యరాశి గల లోహపు దిమ్మె ఉన్నది. దానికి తేలికైన త్రాడు కట్టి బల్ల అంచున ఏర్పాటు చేసిన ఘర్షణ రహిత కప్పీ మీదుగా త్రాడును పంపి ఆ త్రాడు చివర 0.45 కి.గ్రా ద్రవ్యరాశి గల వస్తువును వ్రేలాడదీసినారు. 0.45 కి.గ్రా వస్తువు క్రిందికి జారునపుడు 2 కి.గ్రా. దిమ్మెపై ఒక క్షితిజ సమాంతర బలము పని చేయును. బల్లకు, దిమ్మెకు మధ్యగల ఘర్షణ గుణకం 0.2 అయిన

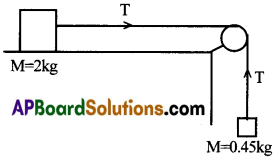
(a) దిమ్మె తొలి త్వరణమును (b) త్రాడులోని తన్యతను (c) దిమ్మె కదిలిన 2 సె. తరువాత త్రాడు తెగిపోయిన
లోహపు దిమ్మె ఎంత దూరం వచ్చి ఆగిపోవును?
సాధన:
లోహపు దిమ్మె ద్రవ్యరాశి M₁ = 2 కి.గ్రా, వ్రేలాడ దీసిన వస్తువు ద్రవ్యరాశి, M₁ = 0.45 కి.గ్రా
ఘర్షణ గుణకం µ = 0.2

(a) M₁ విషయంలో దిమ్మె a త్వరణంతో కుడి వైపునకు ప్రయాణించుచున్నది కనుక, T – µM₁g = M₁a. ….(1)
M₂ విషయంలో M₂ క్రిందికి త్వరణంతో ప్రయాణించును కనుక M₂, M₂g – T = M₂a……….(2)

(c) దిమ్మె విరామ స్థితినుండి బయలు దేరి 2 సెకనులు బల్ల పై పయనించిన తరువాత త్రాడు తెగినది. కనుక 2 సెకనుల తరువాత అనగా త్రాడు తెగు సమయములో లోహపు దిమ్మె వేగం v అయితే u = 0, a = 0.2 మీ/సె², t = 2s v = u + at ప్రకారం ⇒ v = 0 + 0.2 × 2 = 0.4 మీ/సె²

త్రాడు తెగిన తరువాత వస్తువు ఘర్షణకు వ్యతిరేకముగా పని చేయుచూ దూరం ప్రయాణం చేసి ఆగిపోయినది అని అనుకొనిన పనిశక్తి సిద్ధాంతం ప్రకారం చేసిన పని = గతి శక్తిలోని మార్పు

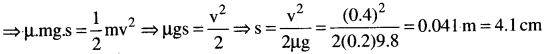
ప్రశ్న 12.
నునుపైన ఒక క్షితిజ సమాంతర తలము పై 10 కి.గ్రా. ద్రవ్యరాశి గల A అను దిమ్మె ఉన్నది. దాని పై 5 కి.గ్రా. ద్రవ్యరాశి గల B అను దిమ్మె ఉన్నది. A,B దిమ్మెల మధ్య ఘర్షణ గుణకం 0.4 పటములో చూపినట్లు దిమ్మె పై 30 న్యూ. బలం ప్రయోగించిరి. అయిన దిమ్మెల మధ్య ఘర్షణ బలం ఎంత?

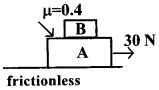
సాధన:
రెండు దిమ్మెలు కలిసి ప్రయాణించుటకు క్రింది దిమ్మె పై ప్రయోగించ గల గరిష్ట బలం
F_max = μ_sg(m_A + m_B) = 0.4 × 10 (10 + 5) = 4 × 15 = 60N
ప్రయోగించిన బలం, ఈ గరిష్ట బలము కన్నా తక్కువగా ఉన్నది. కనుక రెండు దిమ్మెలు కలసి ఒకే త్వరణముతో ప్రయాణించును. ఆ ఉమ్మడి త్వరణం ‘a’ అయితే

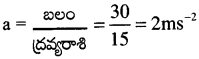
దిమ్మెల మధ్య ఘర్షణ బలం f = m_Ba = 5 × 2 = 10 న్యూ