AP Inter 1st Year Physics Important Questions Chapter 5 Laws of Motion

Students get through AP Inter 1st Year Physics Important Questions 5th Lesson Laws of Motion which are most likely to be asked in the exam.

AP Inter 1st Year Physics Important Questions 5th Lesson Laws of Motion

Very Short Answer Questions

Question 1.
What is inertia? What gives the measure of inertia? [AP 19][IPE’ 14][TS 17,19]
Answer:
Inertia :
Inertia is an inherent property of a body, by which it resists any change in its state. Mass is the measure of inertia.

Question 2.
According to Newton’s third law, every force is accompanied by an equal and opposite force. How can a movement ever take place? [TS 19][AP 15,18]
Answer:
Action and reaction always take place on two different bodies. Hence, they never cancel each other. So movement of bodies is possible.

Question 3.
When a Bullet is fired from a Gun, the Gun gives a kick in fhe backward direction. Explain. [Imp.Q][AP 15]
Answer:
This is due to the ‘law of conservation of momentum’. When a Bullet is fired from a gun, the momentum of the Gun becomes equal and opposite to that of Bullet. So, when the Bullet moves forward, the Gun kicks back. This motion of Gun is called Recoil of the Gun.

Question 4.
Why does a heavy rifle not recoil as strongly as a light rifle using the same cartridge? [Imp.Q]
Answer:
Recoil of the rifle V = \(\frac{mu}{M}\). Here, mass M of rifle
For a heavy rifle, mass M is more which is in the denominator. Hence, its recoil velocity V is less.

Question 5.
If a bomb at rest explodes into two pieces, the pieces must travel in opposite directions. Explain. [TS 15,16,18,22]
Answer:
This is due to the ‘law of conservation of momentum’. Bomb at rest has zero linear momentum. So, when the bomb explodes into two pieces, the sum of their momenta must be equal to zero. So, the two pieces must have equal and opposite momenta. Therefore the pieces must travel in opposite directions.

Question 6.
Define force. What are the basic forces in nature? [Imp.Q]
Answer:
Force is that physical quantity which changes or tries to change the state of a body.
The basic forces in nature are

1. Gravitational force
2. Electromagnetic force
3. Strong nuclear force
4. Weak nuclear force.

Question 7.
Can the coefficient of friction be greater than one? [TS 18]
Answer:
Yes. In general coefficient of friction is less than one. If the surfaces are polished heavily then adhesive forces between the molecules increase and then coefficient of friction will be greater than one.

Question 8.
Why does the car with a flattened tyre stop sooner than the one with inflated tyres? [AP 20][May 13]
Answer:
A flattened tyre gets more deformation. So rolling friction becomes more to that tyre. Hence a car with flattened tyre comes to rest sooner than; car with inflated tyres.

Question 9.
A horse has to exert a greater force during the start of the motion than later. Explain. [AP 16,18,22]
Answer:
Before starting the motior, Horse has static friction and later it will be converted into kinetic friction. Bui, Static friction is more than kinetic friction Hence, Horse has to exert a greater force during the start of the motion than later.

Question 10.
What happens to the coefficient of friction if weight of the body is doubled. [TS’ 19,22] [AP 16,19]
Answer:
Coefficient of friction is independent of weight of the body. So it remains constant.

Short Answer Questions

Question 1.
A stone of mass 0.1kg is thrown vertically upwards. Give the magnitude and direction of the net force on the stone (a) during its upward motion (b) during its downward motion (c) at the highest point, where it momentarily comes to rest.
Answer:
The acceleration due to gravity (g = 9.8ms^-2) is always downward whether the body is rising or falling or it is momentarily at rest at maximum height. Therefore, the net force on the stone in all the three cases is vertically downwards.
m = 0.1kg, g = 9.8 ms^-2.
∴ F = mg = 0.1 × 9.8 = 0.98 N vertically downward

Question 2.
Define the terms momentum and impulse. State and explain the law of conservation of momentum. Give example. [TS 15,18J[AP 20|
Answer:
Momentum :
The product of mass and velocity of a body is called its momentum.
If m is the mass of a body moving with a velocity v then its momentum, p = mv.

Impulse :
The product of the force and time of action of the force that produces a finite change in momentum of the body is called “Impulse”.
I = ∫ Fdt
i.e., Impulse = F_avg × ∆t

Law of conservation of Momentum :
When there is ‘no resultant external force’, the total momentum of all the interacting bodies in a system, remains constant.
In other words, Total momentum before collision = Total momentum after collision

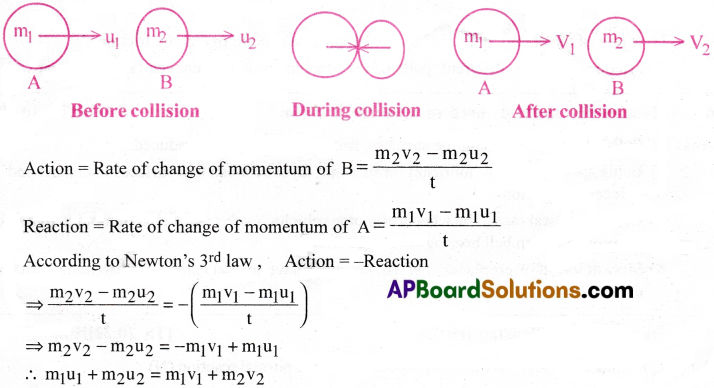
Thus, Total momentum before collision = Total momentum after collision

Ex 1. Explosion of bomb :
When a stationary bomb explodes into two pieces, then according to law of conservation of linear momentum,
Total momentum before explosion = Total momentum after explosion
⇒ 0 = m₁v₁ + m₂v₂ ⇒ m₁v₁ = – m₂v₂
Thus, the momenta of the two pieces after explosion are equal and opposite.

Ex 2. Motion of a Rocket and a Jet plane is according to the law of conservation of momentum.

Question 3.
Why are shock absorbers used in motorcycles and cars?
Answer:
When vehicles move on uneven roads, shock absorbers increase the time of impulse. As a result, impulsive force decreases. Hence, passengers get better comfort.

Question 4.
Explain the terms limiting friction, dynamic friction, and rolling friction. [Imp.Q]
Answer:
1) Limiting friction (f_L) :
It is the maximum value of static friction between the contact surfaces when the body is just ready to slide over a surface.

2) Kinetic/Sliding/dynamic friction (f_k) :
The resistive force encountered by a sliding body on the surface is known as kinetic friction (or) sliding friction.

3) Rolling friction (f_r) :
The resistive force encountered by a rolling body on the surface is known as rolling friction.

Question 5.
Explain the advantages and disadvantages of friction [AP 15,19][TS 15, 17,22]
Answer:
Advantages :

1. We cannot walk without friction between feet and ground.
2. ‘Brakes’ are able to stop the vehicles only due to friction between brake shoes and the inner surface of the brake drum.
3. We are able to pick up a Book only because of friction between Hand and the Book.
4. In a Machine, power is transmitted from the Motor to different parts of the Machine only by using friction between the Belt and the Wheels.

Disadvantages :

1. A part of the energy delivered by the Motor is wasted to overcome friction.
2. Friction between different parts of the Machine produces uneven wear and tear’.

Question 6.
Mention the methods used to decrease friction. [AP 18,22] [TS 16,19]
Answer:
1) Polishing :
By polishing the surfaces, frictional force can be reduced.

2) Using Lubricants :
A lubricant forms a thin layer between two surfaces in contact and it reduces the friction.

3) Using ball bearings :
The wheels of motor vehicles, cycles and shafts of motors, dynamos are provided with ball bearings to reduce friction.

4) Stream lining :
Aeroplanes and Auto mobiles have special construction to reduce friction due to air.

Question 7.
State the laws of rolling friction. [TS 20,22][Imp.Q]
Answer:
1) Rolling friction (fr) is directly proportional to the normal reaction (N)
i.e., f_r ∝ N

Rolling friction (fr is inversely proportional to the radius(r) of the rolling wheel.
i.e., f_r ∝ \(\frac{1}{r}\)
∴ Rolling friction, f_r = \(\frac{\mu_r N}{r}\)
where µ_R = coefficient of rolling friction.

Question 8.
Why is pulling the lawn roller preferred to pushing it? [lmp,Q]
Answer:
Suppose a lawn roller is pulled by a force F making an angle ‘θ’ with the horizontal.

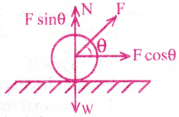
This force can be resolved into two components Fcosθ and Fsinθ.
Total upward force = Total downward force
N + Fsinθ = W ⇒ N = W – Fsinθ
∴ Frictional force f₁ = µN = µi(W-Fsinθ) ………. (1)

Suppose the roller is pushed by the same force F, making angle θ with the horizontal.

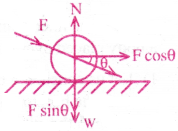
Here, Force can be resolved into two components Fcosθ and Fsinθ.
Total upward force = Total downward force
N = W + Fsinθ
∴ Frictional force f₂ = µN = µ(W + Fsinθ) ………. (2)
From (1) & (2), it is clear that f₁ < f₂.
Hence pulling is preferred than pushing.

Long Answer Questions

Question 1.
(a) State Newton’s Ilnd law of motion. Hence derive the equation of motion F = ma.
(b) A body is moving along a circular path such that its speed always remains constant. Should there be a force acting on the body? [TS 18][Mar 13, May 13][AP 16,17,19]
Answer:
(a) Newton’s Second Law :
“The ‘rate of change of momentum of a body is directly proportional to the external force acting on the body and it is in the direction, in which the force acts”.
Thus, \(\frac{dp}{dt}\) ∝ F

Derivation of F = ma
Let m = mass of the body, v = velocity of the body,
∴ Linear momentum, p = mv
Let F = external force applied on the body in the direction of motion of the body.

Here, k can be made equal to 1, by properly selecting the units of F, m, a.
Then, F = ma.

(b) Yes, there should be a force acting on it.
Reason :
When a body is moving along a circular path, the direction of velocity at a point is along the tangent at that point. So the direction of velocity continuously changes from point to point. So the body has acceleration which is directed towards the centre of the circle. This acceleration is called centripetal acceleration. As there is acceleration, there must be a force acting on the body towards the centre of the circle. This force is called centripetal force.

Question 2.
Define angle of friction and angle of repose. Show that angle of friction is equal to angle of repose for a rough inclined plane.
A block of mass 4kg is resting on a rough horizontal plane and is about to move when a horizontal force of 30N is applied on it. If g = 10ms^-2, find the total contact force exerted by the plane on the
Answer:

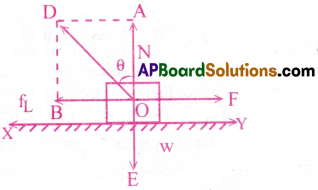
Angle of friction :
The angle which the resultant of force of limiting friction f_L and the normal reaction N makes with the normal reaction N, is called angle of friction.

From the figure, tan θ =\(\frac{AD}{OA}=\frac{f_L}{N}\) = µ_s …………. (1)

Angle of repose :
The angle of repose is the angle which an inclined plane makes with the horizontal when a body placed over it just starts sliding down.
1) Let us consider a body of weight w placed on an inclined plane OA, whose inclination Φ with the horizontal can be changed. The weight of the body w acts vertically downwards through the centre of gravity of the body.

2) Increase the angle of inclination very slowly till the body just begins to slide down the plane. This particular angle of inclination is called the” angle of sliding(or)angle of repose”, represented by Φ. The value of Φ depends upon the material and the nature of the two surfaces in contact.

3) The weight w of the body can be resolved into two components (a) wcosΦ acting perpendicular to the plane and (b) wsinΦ acting parallel to the plane. The component wcosΦ balances the normal reaction N, while the component wsinΦ is equal to the limiting friction f_L.

Hence the tangent of angle of repose is equal to coefficient of static friction.
But µ_s = tanθ, where θ is the angle of friction
∴ tanθ = tanΦ ⇒ θ = Φ
Thus angle of friction is equal to angle of repose.

Problem:

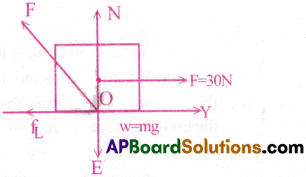
Given m = 4kg and g = 10ms^-2.
∴ weight of the body, w = mg = 4 × 10
= 40 N = normal reaction (N)

Maximum static frictional force, f_L = F = 3 ON
The total contact force (F) on the block by the plane is equal to resultant of N and f_L.

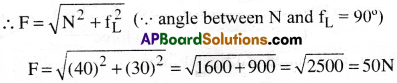
Solved Problems

Question 1.
An astronaut accidentally gets separated out of his small spaceship accelerating in inter stellar space at a constant rate of 100ms^-2. What is the acceleration of the astronaut at the instant after he is outside the spaceship? (Assume that there are no nearby stars to exert gravitational force on him).
Solution:
Since there are no nearby stars to exert gravitational force on him and the small spaceship exerts negligible gravitational attraction on him, the net force acting on the astronaut, once he is out of the spaceship, is zero. By the first law of motion the acceleration of the astronaut is zero.

Question 2.
A bullet of mass 0.04kg moving with a speed of 90 ms-1 enters a heavy wooden block and is stopped after a distance of 60cm. What is the average resistive force exerted by the block on the bullet?
Solution:
The retardation ‘a’ of the bullet (assumed constant) is given by

The retarding force, by the second law of motion, is 0.04kg × 6750 ms^-2 = 270N
The actual resistive force and therefore retardation of the bullet may not be uniform.
The answer, therefore, only indicates the average resistive force.

Question 3.
The motion of a particle of mass m is described by y = ut + \(\frac{1}{2}\)gt². Find the force acting on the particle.
Solution:
We know y = ut + \(\frac{1}{2}\)gt² Now, v = \(\frac{dy}{dt}\) = u + gt, acceleration, a = \(\frac{dv}{dt}\) = g
Then the force is given by F = ma = mg

Question 4.
A batsman hits back a ball straight in the direction of the bowler without changing its initial speed of 12 mr1. If the mass of the ball is 0.15kg, determine the impulse im¬parted to the ball. (Assume linear motion of the ball) [ AP 17][TS 19,20]
Solution:
Change in momentum = (0.15 × 12) – (-0.15 × 12) = 3.6 Ns
Impulse = 3.6 Ns in the direction from the batsman to the bowler.

Question 5.
Determine the maximum acceleration of the train in which a box lying on its floor will remain stationary, given that the coefficient of static friction between the box and the train’s floor is 0.15.
Solution:
The acceleration of the box is due to the static friction.
∴ a_max = µ_sg = 0.15 × 10ms^-2 = 1.5 ms^-2

Question 6.
A cyclist speeding at 18 km/h on a level road takes a sharp circular turn of radius 3 m without reducing the speed. The coefficient of static friction between the tyres and the road is 0.1. Will the cyclist slip while taking the turn?
Solution:
The condition for the cyclist not to slip is given by v² ≤ µ_sRg ………… (1)
Now, v = 18 km/h = 5 ms^-1 ⇒ v² = 25 m²s^-2.
Also, R = 3m, g = 9.8 ms^-2, µ_s = 0.1 ⇒ µ_sRg = 2.94 m²s^-2.
The condition (1) is not obeyed. The cyclist will slip while taking the circular turn.

Exercise Problems

Question 1.
The linear momentum of a particle as a function of time t is given by p = a + bt, where ‘a’ and ‘b’ are positive constants. What is the force acting on the particle?
Solution:
Given linear momentum, p = a + bt
Force, F = ?
Force = rate of change of momentum
F = \(\frac{dp}{dt}\) = \(\frac{d}{dt}\)(a + bt) = b
∴ Force on the body = b

Question 2.
Calculate the time needed for a net force of 5N to change the velocity of a 10kg mass by 2 m/s. [TS 16]
Solution:
Given net force on the body, F = 5N
mass of the body, m = 10kg
change in velocity, v – u = 2 ms^-1
time t = ?

Question 3.
A ball of mass m is thrown vertically upward from the ground and reaches a height h before momentarily coming to rest. If g is acceleration due to gravity, what is the impulse received by the ball due to gravity force during its flight? (neglect air resistance)
Solution:
Ball reaches the maximum height h. So its initial velocity of projection will be u = \(\sqrt{2gh}\)
Initial momentum, Pj = mu = m \(\sqrt{2gh}\) (in the upward direction)
When it reaches the ground, it will have the same velocity, u, but in opposite direction. Hence final momentum, P_f = – mu = – m\(\sqrt{2gh}\)
∴ Magnitude of change in momentum = P_i – P_f
= m\(\sqrt{2gh}\) – (-m\(\sqrt{2gh}\)) = 2m\(\sqrt{2gh}\) = \(\sqrt{8m^2gh}\)
∴ Impulse received by the ball due to gravity force
= change in momentum = \(\sqrt{8m^2gh}\)

Question 4.
A constant force acting on a body of mass 3.0 kg changes its speed from 2.0 ms^-1 to 3.5 ms^-1 in 25s. The direction of motion of the body remains unchanged. What is the magnitude and direction of the force?
Solution:
Given mass of the body, m = 3kg
Initial velocity, u = 2 ms^-1
Final velocity, v = 3.5 ms^-1
Time t = 25 sec
Force F = ?

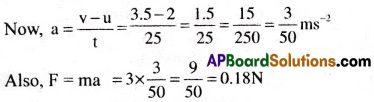
Since velocity of the body is increasing, the direction of force is in the direction of motion of the body.

Question 5.
A man in a lift feels an apparent weight VV when the lift is moving up with a uniform acceleration of 1/3_rd of the acceleration due to gravity. If the same man were in the same lift now moving down with a uniform acceleration that is 1/2 of the acceleration due to gravity, then what is his apparent weight?
Solution:
Let mg be the true weight of the man. When the lift is moving upwards with an acceleration ’a’ then the apparent weight will be mg+ma
In the first case, a = \(\frac{g}{3}\) and apparent weight is w ⇒ w = mg \(\frac{mg}{3}=\frac{4mg}{3}\) ……… (1)

When the lift is moving downwards with an acceleration a then the apparent weight is mg – ma
Given a = g/2.

Question 6.
A container of mass 200kg rests on the back of an open truck. If the truck accelerates at 1.5 m/s², what is the minimum coefficient of static friction between the container and the bed of the truck required to prevent the container from sliding off the back of the truck?
Solution:
The box is accelerating along with the truck.
Therefore, force on the box is F = ma = 200 × 1.5 = 300 N
Since the truck is accelerating in the forward direction the reaction of the container is equal to F = 300 N, but acts in the backward direction.
The backward motion of the container is opposed by the limiting friction between the container and the floor of the truck.

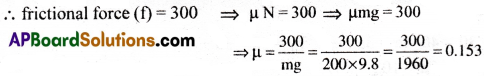
Question 7.
A bomb initially at rest at a height of 40m above the ground suddenly explodes in to two identical fragments. One of them starts moving vertically downwards with an initial speed of 10 m/s. If acceleration due to gravity is 10ms², what is the separation between the fragments 2s after the explosion?
Solution:
The bomb has exploded into two pieces and one piece is moving vertically downwards with a velocity of 10ms^-1. So, according to law of conservation of momentum, the other piece of same mass should travel in the upward direction with a velocity of 10ms^-1.
For that piece, time of ascent (ta) = \(\frac{u}{g}=\frac{10}{10}\) = 1 sec
So in 2sec, it will reach its original position, i.e., it will be at a height of 40m from the ground. The piece which is moving downwards has initial velocity (u) = 10ms^-1
acceleration (a) = g = 10ms^-2
time (t) = 2sec
distance travelled (s) = ?

Now, s = ut + \(\frac{1}{2}\)at² ⇒ s = 10 × 2 + \(\frac{1}{2}\) × 10 × 4 = 20 + 20 = 40m
∴ Distance of separation between the two pieces = 40m

Question 8.
A fixed pulley with a smooth grove has a light string passing over it with a 4 kg attached on one side and a 3kg on the other side. Another 3kg is hung from the other 3kg as shown with another light string. If the system is released from rest, find the common acceleration? (g = 10ms²)

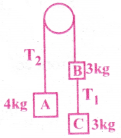
Solution:
When the system is released, A will move upwards and B and C move downwards with common acceleration. Let it be ‘a’.

From eq (2); T₁ + 30 – 40 – 4a = 3a ⇒ T₁ – 4a = 3a + 10
⇒ T₁ – 7a = 10 ……… (4)
From eq (3) T₁ = 30 – 3a
Substituting the value of T| in equaiton (4); T₁ – 7a = 10
⇒ 30 – 3a – 7a = 10
⇒ 30 – 10a = 10 ⇒ 10a = 20 ⇒ a = 2ms^-2.

Question 9.
A block of mass of 2kg slides on an inclined plane that makes an angle of 30° with the horizontal. The coefficient of friction between the block and the surface is √3/2.
(a) What force should be applied to the block so that it moves down without any acceleration?
(b) What force should be applied to the block so that it moves up without any acceleration?
Solution:

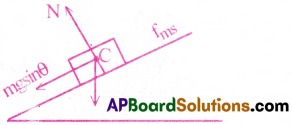
(a) mg sin θ = 2 × 9.8 × sin 30° = 2 × 9.8 × \(\frac{1}{2}\) = 9.8N
Maximum static friction, f_L = µ_sN = µ_smg cosθ
= \(\frac{\sqrt{3}}{2}\) × 2 × 9.8 × cos 30° = \(\frac{\sqrt{3}}{2}\) × 2 × 9.8 × \(\frac{\sqrt{3}}{2}\) = 3 × 4.9 = 14.7N

If F₁ is the force to be applied on the body so that it moves downwards without any acceleration, then
F₁ + mg sin θ = f_L
⇒ F₁ + 9.8 = 14.7
⇒ F₁ = 4.9 N

(b) In this case, the frictional force f_L and mg sinθ act downwards. So the minimum force F required to move the body upwards without acceleration is
F = mg sinθ + f_L = 9.8 + 14.7 = 24.5 N

Question 10.
A block is placed on a ramp of parabolic shape given by the equation y = x²/20. If µ_s = 0.5, what is the maximum height above the ground at which the block can be placed without slipping?
Solution:
Given that µ_s = 0.5

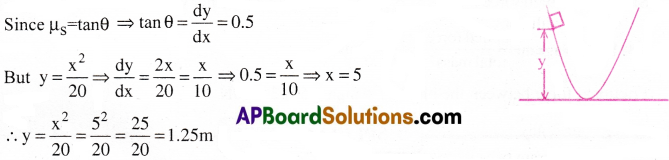
Question 11.
A block of metal of mass 2kg on a horizontal table is attached to a mass of 0.45 kg by a light string passing over a frictionless pulley at the edge of the table. The block is subjected to a horizontal force by allowing the 0.45 kg mass to fail. The coefficient of sliding friction between the block and table is 0.2.

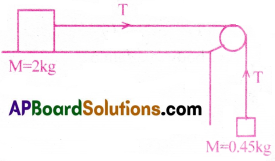
Calculate (a) the initial acceleration (b) the tension in the string (c) the distance the block would continue to move if, after 2s of motion, the string should break.
Solution:
Let M₁ = 2kg, M₂ = 0.5kg
Given that µ = 0.2
(a) For M₁, T – µM₁g = M₁a ……(1)
For M₂, M₂g – T = M₂a ……….. (2)

⇒ T = f + m₂a = |µmg + m₂a = 0.2 × 2 × 9.8 + 2(0.2) = 4.32N

(c) We have u=0, a = 0.2 m/s², t = 2s
The velocity of the block before the string breaks is given by v = u + at
⇒ v = 0 + 0.2 × 2 = 0.4 m/s²
After break if the block travels a distance s then workdone = change in K.E

Question 12.
One a smooth horizontal surface a block A of mass !0kg is kept. On this block a second block B of mass 5kg is kept. The coefficient of friction between the tw o blocks is 0.4. A horizontal force of 30N is applied on the lower block as shown. What is the force of friction between the blocks?

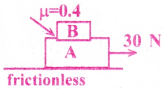
Solution:
The maximum force that can be applied on the lower block so that the two blocks move together is
F_max = µ_sg(m_A + m_B) = 0.4 × 10 (10 + 5) = 4 × 15 = 60N
Since the applied force F = 30N < F_max the blocks move together with a common acceleration ‘a’.

Frictional force between the blocks f = m_Ba = 5 × 2 = 10N

Multiple Choice Questions

1. Gravel is dropped into a conveyor belt at rate of 0.5 kg/sec. The extra force required in newtons, to keep the belt in moving at 2m/s is
1) 1
2) 2
3) 4
4) 5
Answer:
1) 1

2. A body of 50 kg in lift moving down with an acceleration of 9.8ms^-2. The apparent weight of the body is (g = 9.8ms^-2)
1) 509.8N
2) 0
3) 50 N
4) \(\frac{50}{9.8}\) N
Answer:
2) 0

3. A machine gun fires 20 bullets per second into a target. Each bullet weighs 150g and has a speed of 800 m/s. The force necessary to hold the gun is
1) 800 N
2) 1000 N
3) 1200 N
4) 2400N
Answer:
4) 2400N

4. A body of mass 2kg is acted upon by two forces each of magnitude 1 newton making an angle of 60″ with each other. The net acceleration of the body is
1) 0.5
2) 1.0
3) √3/2
4) √2/3
Answer:
3) √3/2

5. A man of mass 20kg standing in an elevator whose cable broke suddenly. If the elevator falls freely, the force exerted by the floor of the elevator on the man is
1) 20 N
2) 10 N
3) 0
4) 6 N
Answer:
3) 0

6. A gun fires a bullet of mass 50gm with a velocity of 30 m/s. This gun is pushed back with a velocity of Im/s, then mass of the gun is
1) 3.5 kg
2) 30 kg
3) 1.5 kg
4) 20 kg
Answer:
3) 1.5 kg

7. A man fires a bullet of mass 200 g at a speed of 5 m/s. The gun is of one kg mass. By what velocity the gun rebounds backward?
1) 1 m/s
2) 0.01 m/s
3) 0.1 m/s
4) 10 m/s
Answer:
1) 1 m/s

8. Physical independence of force is a consequence of
1) third law’ of motion
2) second law of motion
3) first law of motion
4) all of these laws
Answer:
3) first law of motion

9. A shell, in flight, explodes into four unequal parts. Which of the following is conserved?
1) Potential energy
2) Momentum
3) Kinetic energy
4) Both (1) and (3).
Answer:
2) Momentum

10. A 10 N force is applied on a body produce in it an acceleration of 1 m/s². The mass of the body is
1) 15 kg
2) 20 kg
3) 10 kg
4) 5 kg
Answer:
3) Kinetic energy

11. A body, under the action of a force F = \(6\hat{i}-8\hat{j}+10\hat{k}\) acquires an acceleration of 1 m/s². The mass of this body must be
1) 10 kg
2) 20 kg
3) 10√2 kg
4) 2√10 kg
Answer:
3) 10√2 kg

12. A force vector applied on a mass is represented as \(\overrightarrow{F}=6\hat{i}-8\hat{j}+10\hat{k}\) and accelerates with 1 m/s². What will be the mass of the body?
1) 10 kg
2) 20 kg
3) 10√2 kE
4) 2√10 kg
Answer:
3) 10√2 kE

13. A cricketer catches a ball of mass 150 gm in 0.1 sec moving with speed 20 m/s, then he experiences force of
1) 300 N
2) 30 N
3) 3 N
4) 0.3 N
Answer:
2) 30 N

14. A body of mass M hits normally a rigid wall with velocity V and bounces back with the same velocity. The impulse experienced by the body is
1) MV
2) 1.5MV
3) 2MV
4) zero
Answer:
3) 2MV

15. A rigid ball of mass m strikes a rigid wall at 60° and gets reflected without loss of speed as shown in the adjacent figure. The value of impulse imparted by the wall on the ball will be

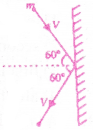
1) mV
2) 2 mV
3) mV/2
4) mV/3
Answer:
2) 2 mV

16. A ball of mass 0.15 kg is dropped from a height 10 m, strikes the ground and rebounds to the same height. The magnitude of impulse imparted to the ball is (g = 10 m/s²) nearly
1) 1.4 kg m/s
2) 0 kg m/s
3) 4.2 kg m/s
4) 2.1 kg m/s
Answer:
3) 4.2 kg m/s

17. The force F acting on a particle of mass m is indicated by the force-time graph as shown.

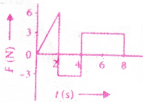
The change in momentum of the particle over the time interval from zero to 8 s is
1) 24 Ns
2) 20 Ns
3) 12 Ns
4) 6 N s
Answer:
3) 12 Ns

18. A stone is dropped from a height h. It hits the ground with a certain momentum P. If the same stone is dropped from a height 100% more than the previous height, the momentum when it hits the ground will change by
1) 68%
2) 41%
3) 200%
4) 100%
Answer:
2) 41%

19. A mass of 1 kg is thrown up with a velocity 100m/s. After 5 seconds, it explodes into two parts. One part of mass 400 g comes down with a velocity 25 m/s. The velocity of other part is (Take g = 10 ms^-2)
1) 40 m/s
2) 80 m/s
3) 100 m/s
4) 60 m/s
Answer:
3) 100 m/s

20. A 500 kg car takes a round turn of radius 50 m with a velocity of 36 km/hr. The centripetal force is
1) 1000 N
2) 750 N
3) 250 N
4) 1200N
Answer:
1) 1000 N

21. A block slides down a rough inclined plane of inclination 45″. If coefficient of kinetic friction is 0.5, then acceleration of the sliding block is

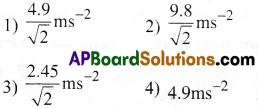
Answer:
1

22. A body of weight 50 N is placed on a surface. If the force required to move the body on the surface is 30N, the coefficient of friction is
1) 0.6
2) 1.2
3) 0.3
4) 1.67
Answer:
1) 0.6

23. A particle is projected up along a rough inclined plane of inclination 45° with the horizontal. If the coefficient of friction is 0.5, the retardation is

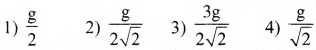
Answer:
3

24. A car of mass rn is moving on a level circular track of radius R. If u represents the static friction between the road and tyres of the car, the maximum speed of the car in circular motion is given by

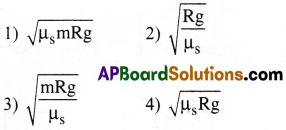
Answer:
4

25. A conveyor belt is moving at a constant speed of 2ms^-1. A box is gently dropped on it. The coefficient of friction between them is p = 0.5. The distance that the box will move relative to belt before coming to rest on it, taking g = 10 ms^-2, is
1) 0.4 m
2) 1.2 m
3) 0.6 m
4) zero
Answer:
1) 0.4 m

26. A car of mass 1000 kg negotiates a banked curve of radius 90 m on a friction less road. If the banking angle is 45°, the speed of the car is
1) 20ms^-1
2) 30 ms^-1
3) 5 ms^-1
4) 10 ms^-1
Answer:
2) 30 ms^-1

27. A car is moving in a circular horizontal track radius 10 m with a constant speed of 10 m/s. A bob is suspended from the roof of the car by a light wire of length 1,0 m. The angle made by the wire with the vertical is
1) π/3
2) π/6
3) π/4
4) 0°
Answer:
3) π/4

28. A roller coaster is designed such that riders experience “weightlessness” as they go round the top of a hill whose radius of curvature is 20 m. The speed of the car at the top of the hill is between
1) 16 m/s and 17 m/s
2) 13 m/s and 14 m/s
3) 14 m/s and 15 m/s
4) 15 m/s and 16 m/s
Answer:
3) 14 m/s and 15 m/s

29. When milk is churned, cream gets separated due to
1) centripetal force
2) centrifugal force
3) frictional force
4) gravitational force
Answer:
2) centrifugal force

30. A small block slides down on a smooth inclined plane, starting from rest at time t = 0. Let S_n be the distance travelled by the block in the interval t = n – 1 to t = n. Then, the ratio \(\frac{S_n}{S_{n+1}}\)

Answer:
3

31. A man weighs 80 kg. He stands on a weighing scale in a lift which is moving upwards with a uniform acceleration of 5 m/s². What would be the reading on the scale? (g = 10 m/s²)
1) zero
2) 400 N
3) 800 N
4) 1200 N
Answer:
4) 1200 N