AP Inter 1st Year Physics Important Questions Chapter 3 Motion in a Straight Line

Students get through AP Inter 1st Year Physics Important Questions 3rd Lesson Motion in a Straight Line which are most likely to be asked in the exam.

AP Inter 1st Year Physics Important Questions 3rd Lesson Motion in a Straight Line

Very Short Answer Questions

Question 1.
The states of rest and motion are relative. Explain. [Imp.Q]
Answer:
For a person travelling in a train, the co-passengers appear to be at rest, but objects outside the train like electric poles, trees etc, appear to be moving backwards. Where as, for a person on the platform the electric poles, trees etc. appear to be at rest but the train appears to be moving. So the states of rest and motion are relative.

Question 2.
How is average velocity different from instantaneous velocity? [Mar 13]
Answer:
The average velocity during a time interval does not tell us how fast or in what direction the body is moving at any given time during the time interval. Where as instantaneous velocity gives the idea of fastness and the direction of motion of the body. In uniform motion, both are equal.

Question 3.
Give an example of a case, where the velocity of an object is zero, but its acceleration is not zero. [|Imp.Q| Mar 13]
Answer:
In the case of a vertically projected body at the Maximum height, its velocity is zero but it has acceleration due to gravity in the downward direction.

Question 4.
A vehicle travels half the distance L with speed v₁ and the other half with speed v₂ What is the average speed?
Answer:

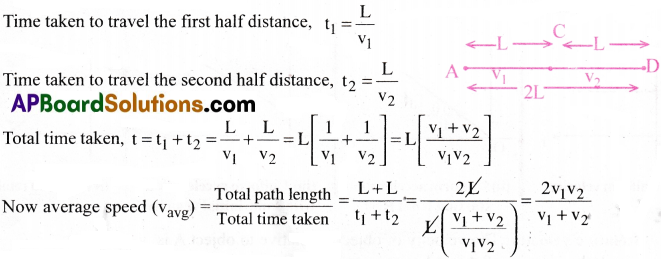
Question 5.
A lift coming down is just about to reach tjie ground floor. Taking the ground floor as origin and positive direction upwards for all quantities, which one of the following is correct?
(a) x < 0, v < 0, a > 0 (b) x > 0, v < 0, a < 0 (c) x > 0, v < 0, a > 0 (d) x > 0, v > 0, a > 0
Answer:

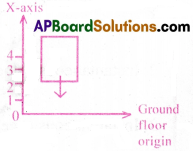
If x denotes the displacement of the lift, then it will be negative.
i.e, x < 0 (displacement = final reading – initial reading)
As the lift is moving downwards, its velocity is directed downwards.
So v < 0 When the lift is about to touch the ground floor, its velocity gets decreased. So its acceleration is in the upward direction, i.e., a > 0. (a) is correct

Question 6.
A uniformly moving cricket ball is hit with a bat for a very short time and is turned back. Show the variation of its acceleration with time, taking the acceleration in the backward direction as positive.
Answer:
The graph for the given motion is as shown in the tig.

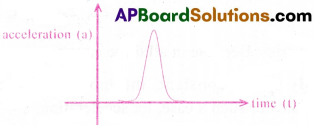
Question 7.
Give example of one-dimensional motion, where the particle moving along positive x-direction comes to rest periodically and moves forward.
Answer:
Consider the position of the particle at any time ‘t’ is given by x = t – sint
⇒ velocity (v) = \(\frac{dx}{dt}\) = 1 – cos t
Since cost< 1, v is positive i.e, the particle moves forward.
When t=0, v=0, i.e, the particle comes to rest

Question 8.
An object falling through a fluid is observed to have an acceleration given by a = g – bv where g is the gravitational acceleration and b is a constant. After a long time it is observed to fall with a constant velocity. What would be the value of this constant velocity?
Answer:
When velocity becomes constant, acceleration, a = 0 ⇒ 0 = g -bv ⇒ bv = g (or) v = g/b
∴ The constant velocity is v = \(\frac{g}{b}\)

9. If the trajectory of a body is parabolic in one frame, can it be parabolic in another frame that moves with a constant velocity with respect to the first frame? if not, what can it be?
Answer:
It will not be parabolic from the second reference frame. It appears to move in a straight line.

Reason:
The horizontal component of projectile and the velocity of second reference frame are constants. So the person in the second reference frame will observe only the vertical component of velocity of the projectile. As it decreases till the projectile reaches maximum height and then increases, the body will appear as though it is thrown vertically upwards with velocity usinθ where u is the velocity of projection and θ is the angle of projection.

Question 10.
A spring with one end attached to a mass and the other to a rigid support is stretched and released. When is the magnitude of acceleration a maximum?
Answer:
When the spring is stretched and released, the mass executes S.H.M. In S.H.M. Acceleration is directly proportional to displacement. Hence the mass will have maximum acceleration at extreme positions.

Short Answer Questions

Question 1.
Can the equations of kinematics he used when t lie acceleration varies with time? If not, what form would these equations take?
Answer:
No. The equations of kinematics [v = v₀ + at, s = v₀t + \(\frac{1}{2}\)at², v² -v₀² = 2as, s_n = v₀ + a(n – \(\frac{1}{2}\))]cannot be used when the acceleration varies. Because in all these equations, acceleration is constant.

If the acceleration of a body is not constant, the motion of such a body is called non-uniformly accelerated motion. For such a case, let acceleration, a ∝ = t_n
Thus a = kt_n or \(\frac{dv}{dt}\) = kt_n ⇒ dv = kt_ndt ………. (1)
When t = 0, u = v₀ (initial velocity) and where k is a constant, when t = t, v = v (final velocity)

Question 2.
Derive the equation S = ut + \(\frac{1}{2}\)at² from v – t graph.
Answer:

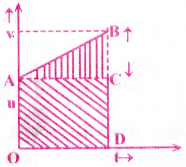
A graph is drawn between v & t for uniformly accelerated motion. The area under v-t curve gives the displacement.
So Area between the instants 0 to t = Area of triangle ABC + Area of rectangle OACD
S = ut + \(\frac{1}{2}\)(v -u)t
S = ut + \(\frac{1}{2}\)(at)t (∵ v – u = at)
∴ S = ut + \(\frac{1}{2}\)at²

Question 2.
A particle moves in a straight line with uniform acceleration. Its velocity at time t = 0 is v₁ and at time t = t is v₂. The average velocity of the particle in this time interval is \(\frac{v_1+v_2}{2}\). Is this correct? substantiate your answer.
Answer:

Question 3.
Can the velocity of an object be in a direction other than the direction of acceleration of the object? If so, give an example. [TS 22]
Answer:
Yes, the velocity of an object can be in a different direction other than that of acceleration.
Ex :
1) When a body is projected vertically upwards, the direction of velocity is upwards where as the direction of acceleration is downwards.
2) Incaseof oblique projectile motion, velocity is always tangential to the path followed by the projectile, whereas the gravitational acceleration is always downward.

Question 4.
A parachutist flying in an aeroplane jumps when it is at a height of 3 km above ground. He opens his parachute when he is about 1km above ground. Describe his motion. [TS 17]
Answer:

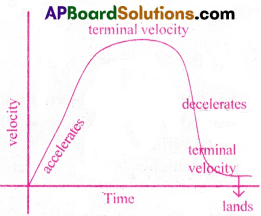
A parachutist flying in an aeroplane jumps when it is at a height ot 3km above the ground. Upto 2 km he travels under gravity. At a height lkm above the ground the parachute opens. Once the parachute ( pens air resistive force acts on parachutist in upward direction and grav itational force acts on him in downwards. After travelling certaind istance both forces are equal and net force on him is zero. So his acceleration is zero. At which he attains constant velocity called “Terminal Velocity”. Then the parachutist reaches the ground safely.

Question 5.
A bird holds a fruit in its beak and flies parallel to the ground. It lets go of the fruit at some height. Describe the trajectory of the fruit as it falls to the ground as seen by (a) the bird and (b) a person on the ground. [TS 22]
Answer:
(a) To the bird, the fruit appears to fall in a straight line path.
Reason :
In horizontal direction, the bird and the fruit will have same velocity. So they will travel equal distances in equal intervals of time. So the fruit always appears just below the bird.

(b) To a person on the ground, the fruit will appear to follow a parabolic path.
Reason:
When the bird, flying horizontally, leaves the fruit, the fruit will have a velocity in horizontal direction. This velocity remains constant because no forces are acting on it in horizontal direction. But in vertical direction it has acceleration due to gravity. So the fruit appears to follow a parabola path.

Question 6.
A man runs across the roof of a tali building and jumps horizontally on to the lower roof of an adjacent building. If his speed is 9ms^-1 and the horizontal distance between the buildings is 10m and the height difference between the roofs is 9m, will he be able to land on the nest building? (g = 10ms^-2) [TS 18]
Answer:

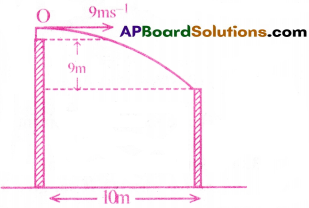
If his horizontal range is greater than 10m, then he can land safely on the other building.
In vertical direction,
initial velocity (u) = 0
uniform acceleration (a) = +g = + 10ms^-2
distance travelled (s) = height difference = 9m
time taken (t) = ?
From S = ut + \(\frac{1}{2}\)at²

Now horizontal range = horizontal velocity × time of fall = 9 × 1.34- 12.08m ≈ 12.1 m
Since he can jump upto nearly 12.1m, so he can safely land on the roof of adjacent building.

Question 7.
A ball is dropped from the roof of a tall building and simultaneously another ball is thrown horizontally with some velocity from the same roof. Which ball Sands first? Explain your answer. [TS 15]
Answer:
For a dropped body:

If a body is dropped from a tower of height ‘h’
Initial velocity u = 0, accelerations a = + g, displacement s = h
Let time of jouney be t₁ ; from s = ut + \(\frac{1}{2}\)at²h = 0 + \(\frac{1}{2}\)gt₁² t₁ = \(\sqrt{\frac{2 h}{g}}\)

For horizantally projected body:

If a body is projected horizontally from a tower of height ‘h’
Initial vertical velocity u_y = 0, Initial vertical displacement s = h
acceleration a_y = g, Let time of journey bt t₂
from s = ut + \(\frac{1}{2}\)at² ⇒ h = 0 + \(\frac{1}{2}\)gt₂² ⇒ t₂ = \(\sqrt{\frac{2 h}{g}}\)
As t₁ = t₂ both the bodies reach to the ground simultaneously

Question 8.
A ball is dropped from a building and simultaneously another ball is projected upward with some velocity. Describe the change in relative velocities of the balls as a function of time. [lmp.Q]
Answer:
Suppose the ball ‘A’ is falling freely. So its initial velocity, u_A = 0
Suppose the ball ‘B’ is projected upwards with a velocity ‘u’,

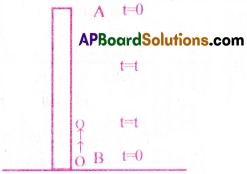
so its initial velocity, u_B = u
Relative velocity of A w.r.t. B is u_AB = u_A – u_B = 0 – u = -u
After some time t, the velocity of A will be v_A = u + at
v_A = 0 + gt
v_A = gt

the velocity of B will be v_B = u – gt
Now, Relative velocity of A w.r.t. B is v_AB = V_A – V_B
= gt- u + gt = 2gt – u

Change in relative velocity of A w.r.t. B in time t is given by
(2gt – u) – (-u) = 2gt – u + u = 2gt
∴ Their change in relative velocities will be 2gt

Question 9.
A typical raindrop is about 4mm in diameter. If a raindrop falls from a cloud which is at I km above the ground, estimate its momentum when it hits the ground.
Answer:
If the rain drop is supposed not attained terminal velocity, when it is falling from the cloud, then the velocity with which it hits the ground can be calculated as follow:
Initial velocity (u) = 0; acceleration (a) = g = 9.8ms^-2
distance travelled (s) = 1km = 1000m; Final velocity (v) = ?
v² – u² = 2as ⇒ v = \(\sqrt{2gh}\) = \(\sqrt{2\times9.8\times1000}\) = 140ms^-1
Now radius of rain drop, r = \(\frac{4mm}{2}\) = 2mm = 2 × 10^-3m
Volume of the rain drop (Spherical in shape), V = \(\frac{4}{3}\)πr³
V = \(\frac{4}{3}\times\frac{22}{7}\) × (2 × 10^-3)³ = 33.52 × 10^-9m³

Let us take, density of water (d) = 1000 kg /m³
∴ Mass of rain drop, m = volume of drop × density = 33.52 × 10^-9 × 1000 = 33.52 × 10^-6 kg
= 33.52 × 10^-6 × 140 = 4692 × 10^-6
= 0.00469 ku ms^-1

Question 10.
Show that the maximum height reached by a projectile launched at an angle 45° is one quarter of the range. [AP 16,19]
Answer:
The horizontal distance travelled by a projectile during its time of flight is called Range.

Thus , maximum Fleight is one quarter of the Range.
NOTE: Please note that, (10) problem is related to the next chapter (Motion in a Plane)

Exercise Problems

Question 1.
A man walks on a straight road from his home to a market 2.5 km away with a speed of 5 kmh^-1. Finding the market closed, he instantly turns and walks back home with a speed of 7.5 kmh^-1. What is the (a) magnitude of average velocity and (b) average speed of the man over the time interval 0 to 50 min. [AP 18,19][TS 20]
Solution:

Question 2.
A car travels the first third of a distance with a speed of lOkmph, the second third at 20kmph and the last third at 60kmph. What is its mean speed over the entire distance? [AP 18, 22][IPE’ 14][TS 16, 18]
Solution:
Let the total distance = 3S km

Question 3.
A bullet moving with a speed of 150 ms-1 strikes a tree and penetrates 3.5 cm before stopping. What is the magnitude of its retardation in the tree and the time taken for it to stop after striking the tree? |May 13]
Solution:
Initial speed of the bullet, (u) = 150 ms^-1.
Distance travelled in the tree before stopping (s) = 3.5 cm = 3.5 × 10^-2 m
Final velocity (v) =0; acceleration (a) =?; time taken to stop (t) = ?
Now, v² – u² = 2as ⇒ (0)² – (150)² = 2 × a × 3.5 × 10^-2.

Question 4.
A motorist drives north for 30 min at 85 km/h and then stops for 15min. He continues travelling north and covers 130 km in 2 hours. What is his total displacement and average velocity?
Solution:
Distance travelled during 30 minutes, S₁ = speed × time = \(\frac{85km}{hr}\) × 30min = \(\frac{85km}{hr}\) × \(\frac{1}{2}\)hr = 42.5km

Distance travelled during 2 hours, S₂ = 130 km
Since motorist travelled in the same direction i.e., north,
total displacement(s) = total distance travelled
⇒ s = 42.5 + 130 = 172.5 km

Question 5.
A ball A is dropped from the top of a building and at the same time an identical ball B is thrown vertically upward from the ground. When the balls collide the speed of A is twice that of B. At what fraction of the height of the building did the collision occur?
Solution:

Question 6.
Drops of wafer fall at regular intervals from the roof of a building of height 16m. The first drop strikes the ground at the same moment as the fifth drop leaves the roof. Find the distances between successive drops.
Solution:

Distance between 1^st and 2^nd drops = S₁ – S₂ = 16 – 9 = 7 m
Distance between 2^nd and 3^rd drops = S₂ – S₃ = 9 – 4 = 5 m
Distance between 3^rd and 4^th drops = S₃ – S₄ = 4 – 1 = 3 m
Distance between 4^th and 5^th drops = S₄ – 0 = 1 – 0 = lm

Question 7.
A hunter aims a gun at a monkey hanging from a tree some distance away. The monkey drops from the branch at the moment he fires the gun hoping to avoid the bullet. Explain why the monkey made a wrong move.
Solution:

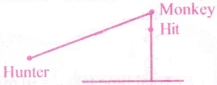
The bullet is like a horizontal projectile and its path traces the parabolic motion, instead of a straight line.
If the monkey jumps down from the branch then the bullet may hit the monkey at some instant as shown in the diagram.

Question 8.
A food packet is dropped from an aeroplane, moving with a speed of 360 kmph in a horizontal direction, from a height of 500m. Find (i) its time of descent (ii) the horizontal distance between the point at which the food packet reaches the ground and the point above which it was dropped.
Solution:
Let the origin of the co-ordinate system is on the ground, directly under the position of the plane when it drops the bomb.

(i) The time t taken by the food packet to reach the ground will be determined from the vertical motion of the bomb. In the vertical direction, initial velocity (u)=0,
distance travelled (s) = h = 500m acceleration (a) = g = 10ms^-2 time taken (t) = ?
Now, s = ut + \(\frac{1}{2}\)at² ⇒ 500 = 0 + \(\frac{1}{2}\) × 10 × t² ⇒ 500 = 5t² ⇒ t² = 100 ⇒ t = 10 s

(ii) The initial horizontal velocity of food packet remains constant.
Horizontal distance = Horizontal velocity × time of travel = 100 × 10 = 1000m

Question 9.
A ball is tossed from the window of a building with an initial velocity of 8 ms^-1 at an angle of 20″ below the horizontal. It strikes the ground 3s later. From what height was the ball thrown? flow far from the base of the building does the ball strike the ground?
Solution:
In the vertical direction, initial velocity (u) = 8 sin20° = 8 × 0.3420 = 2.736 ms^-1.
Time (t) = 3 s acceleration (a) = g = 9.8 ms^-2. Required height = distance s = ?
Now s = ut + \(\frac{1}{2}\)at² = 2.736 × 3 + \(\frac{1}{2}\) × 9.8 × 9 = 8.208 + 44.1 = 52.3m
∴ height of the window = 52. 3m

The distance of the point where the hall strikes on the ground, from the base of building
= 8cos20° × 3 = 8 × 0.9397 × 3 = 7.5176 × 3 = 22.6 m

Question 10.
Two balls are projected from the same point in directions 30° and 60″ with respect to the horizontal. What is the ratio of their initial velocities if they (a) attain the same height? (b) have the same range? [AP 17]
Solution:
(a) Let ut and u₂ be their initial velocities.
Given, maximum height of 1^st body = maximum height of 2^nd body

Question 11.
A ball is thrown vertically upwards with a velocity of 20 ms^-1 from the top of a multistorey building. The height of the point from where the ball is thrown in 25.0m from the ground.(a) How high will the ball rise? (b)How long will it be before the ball hits the ground. Take g = 10 ms^-2 [Actual value of ‘g’ is 9.8 ms^-2] [AP 15; TS 15, 19]
Solution:

Question 12.
A car moving along a straight high way with speed of I26km/h is brought to a stop within a distance of 200m. What is the retardation of the car (assumed uniform) and how long does it take for the car to stop? [AP 20]
Solution:

Multiple Choice Questions

1. A car covers the first half of the distance between two places at 40 km/h and another half at 60 km/h. The average speed of the car is
1)40 km/h
2) 48 km/h
3) 50 km/h
4) 60 km/h
Answer:
2) 48 km/h

2. A car moves a distance of 200 m. It covers the first half of the distance at speed 40 km/h and the second half of distance at speed v. The average speed is 48 km/h. The value of v is
1) 56 km/h
2) 60 km/h
3) 50 km/h
4) 48 km/h
Answer:
2) 60 km/h

3. A particle covers half of its total distance with speed v₁ and the next half distance with speed v₂. Its average speed during the complete journey is

Answer:
3

4. A bus travelling the first one-third distance at a speed of 10 km/h, the next one-third at 20 km/h and at last one-third at 60 km/h. The average speed of the bus is
1) 9 km/h
2) 16 km/h
3) 18 km/h
4) 48 km/h.
Answer:
3) 18 km/h

5. A car runs at a constant speed on a circular track of radius 100 m, taking 62.8 seconds for every circular lap. The average velocity and average speed for each circular lap respectively is
1) 10 m/s, 0
2) 0, 0
3) 0, 10 m/s
4) 10 m/s, 10 m/s
Answer:
3) 0, 10 m/s

6. The distance travelled by a freely falling body in first, second and third second of its fall are in the ratio
1) 1:2:3
2) 1:3:5
3) 1:4:9
4) 1:1:1
Answer:
2) 1:3:5

7. In the presence of considerable resistance of air, a stone is thrown up. If the time of ascent is t, and that of descent is t2, then
1) t₁ > t₂
2) t₁ = 2t₂
3) t₁ < t₂
4) t₁ = t₂
Answer:
1) t₁ > t₂

8. From a place where g = 9.8ms^-2, a stone is thrown up with a velocity of 4.9ms^-1. The time taken for the stone to return to the earth is
1) 1 s
2) 1.5 s
3) 3 s
4) 2.5s
Answer:
1) 1 s

9. A body falling for 2s covers a distance S equals to that covered in next second. If g = 10ms^-2, S =
1) 30m
2) 10 m
3) 60 m
4) 20 m
Answer:
1) 30m

10. If a body loses half of its velocity on penetrating 3 cm in a wooden block, then how much will it penetrate more before coming to rest?
1) 1 cm
2) 2 cm
3) 3 cm
4) 4 cm
Answer:
1) 1 cm

11. A car moves along a straight line whose motion is given by S = 12t + 3t² – 2t³ where S is in metres and’t’ is in seconds. The velocity of the car at the start will be
1) 7 m/s
2) 9 m/s
3) 12 m/s
4) 16 m/s
Answer:
3) 12 m/s

12. A particle moves along a straight line such that its displacement at any time t is given by s = (t³ – 6t² + 3t + 4) metres. The velocity when the acceleration is zero is
1) 3 m/s
2) 42 m/s
3) -9 m/s
4) -15 m/s
Answer:
3) -9 m/s

13. The position x of a particle varies with time, (t) as x = at² – bt³. The acceleration will be zero at time t is equal to
1) a/3b
2) zero
3) 2a/3b
4) a/b
Answer:
1) a/3b

14. If a car at rest accelerates uniformly to a speed of 144 km/h in 20 s, it covers a distance of
1) 1440 cm
2) 2980 cm
3) 20 m
4) 400 m
Answer:
4) 400 m

15. A particle is thrown vertically upward. Its velocity at half of the height is 10 m/s, then the maximum height attained by it (g = 10 m/s²)
1) 8m
2) 20 m
3) 10 m
4) 16 m
Answer:
3) 10 m

16. The velocity of train increases uniformly from 20 km/h to 60 km/ h in 4 hours. The distance travelled by the train during this period is [NEET Q]
1) 160 km
2) 180 km
3) 100 km
4) 120 km
Answer:
1) 160 km

17. The distance travelled by a particle starting from rest and moving with an acceleration 4/3 ms^-2, in the third second is f
1) 10/3m
2) 19/3 m
3) 6 m
4) 4 m
Answer:
1) 10/3m

18. A particle starts its motion from rest under the action of a constant force. If the distance covered in first 10 seconds is S₁ and that covered in the first 20 seconds is S₂, then
1) S₂ = 3S₁
2) S₂ = 4S₁
3) S₂ = S₁
4) S₂ = 2S₁
Answer:
2) S₂ = 4S₁

19. A particle moves in a straight line with a constant acceleration. It changes its velocity from 10 ms^-1 to 20 ms^-1 while passing through a distance 135 m in t second. The value of t is
1) 12
2) 9
3) 10
4) 1.8
Answer:
2) 9

20. A train of 150 metre length is going towards north direction at a speed of 10 m/s. A parrot flies at the speed of 5 m/s towards south direction parallel to the railways track. The time taken by the parrot to cross the train is
1) 12 s
2) 8 s
3) 15 s
4) 10 s
Answer:
4) 10 s

21. A body starts from rest, what is the ratio of the distance travelled by the body during the 4lh and 3rd second?
1) 7/5
2) 5/7
3) 7/3
4) 3/7
Answer:
1) 7/5

22. What will be the ratio of the distance moved by a freely falling body from rest in 4th and 5,h seconds of journey?
1) 4:5
2) 7:9
3) 16:25
4) 1:1.
Answer:
2) 7:9

23. A boy standing at the top of a tower of 20m height drops a stone. Assuming g = 10 m s^-2, the velocity wish which it hits the ground is
1) 10.0 m/s
2) 20.0 m/s
3) 40.0 m/s
4) 5.0 m/s
Answer:
2) 20.0 m/s

24. A ball is thrown vertically upward. It has a speed of 10 m/sec when it has reached one half of its maximum height. How high does the ball rise? (Take g = 10 m/s²)
1) 10 m
2) 5m
3) 15 m
4) 20 m
Answer:
1) 10 m

25. Two bodies A (of mass 1 kg) and B (of mass 3 kg) are dropped from heights of 16 m and 25 m, respectively. The ratio of the time taken by them to reach the ground is
1) 4/5
2) 5/4
3) 12/5
4) 5/12
Answer:
1) 4/5