AP Inter 1st Year Physics Important Questions Chapter 4 సమతలంలో చలనం

Students get through AP Inter 1st Year Physics Important Questions 4th Lesson సమతలంలో చలనం which are most likely to be asked in the exam.

AP Inter 1st Year Physics Important Questions 4th Lesson సమతలంలో చలనం

Very Short Answer Questions (అతిస్వల్ప సమాధాన ప్రశ్నలు)

ప్రశ్న 1.
ఒక సదిశ నిలువు అంశం దాని క్షితిజ సమాంతర అంశానికి సమానం. ఆ సదిశ X-అక్షంతో చేసే కోణం ఎంత? [AP 19][TS 18][Imp.Q]
జవాబు:
\(\overrightarrow{R}\) అనే సదిశ X-అక్షంతో ‘θ’ కోణం చేస్తుంటే
\(\overrightarrow{R}\) యొక్క లంబాంశం \(\overrightarrow{R}\) = R sinθ
\(\overrightarrow{R}\) యొక్క సమాంతర అంశం = R cosθ
∴ Rcosθ = Rsinθ ⇒ tane = 1 ⇒ θ = 45°

ప్రశ్న 2.
ఒక సదిశ \(\overrightarrow{v}\) క్షితిజ సమాంతరంతో θ కోణం చేస్తుంది. ఆ సదిశను θ కోణం భ్రమణం చెందించడమైనది. ఈ భ్రమణం సదిశ \(\overrightarrow{v}\) లో మార్పు తెస్తుందా?
జవాబు:
సదిశను ‘θ’ కోణంతో తిప్పినపుడు దాని పరిమాణం మారదు. కాని దిశ మారుతుంది. అనగా సదిశ \(\overrightarrow{v}\) మారినట్లు.

ప్రశ్న 3.
3 యూనిట్లు, 5 యూనిట్లు పరిమాణం గల రెండు బలాలు ఒకదానితో ఒకటి 60° కోణం చేస్తున్న వాటి ఫలిత పరిమాణం ఎంత? [TS 22][AP 15,16,17]
జవాబు:
P = 3 మరియు Q = 5 మరియు θ = 60° ⇒ cosθ = cos60° = 1/2

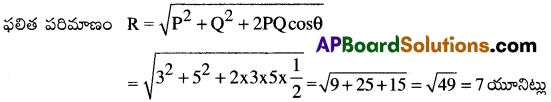
ప్రశ్న 4.
\(\overrightarrow{A}=\overrightarrow{i}+\overrightarrow{j}\) ఈ సదిశ x-అక్షంతో చేసే కోణం ఎంత? [Imp.Q][AP 20,22][TS 17,20]
జవాబు:

ప్రశ్న 5.
7 యూనిట్లు, 24 యూనిట్లు పరిమాణం గల రెండు సదిశలు ఒక దానితో ఒకటి లంబకోణం చేస్తున్న వాటి ఫలిత సదిశ పరిమాణం ఎంత? [IPE’14][Imp.Q][AP 16,18]
జవాబు:
P = 7 మరియు Q = 24; θ = 90° ⇒ cosθ = cos90° = 0

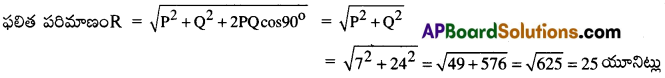
ప్రశ్న 6.
\(\overrightarrow{P}=2\overrightarrow{i}+4\overrightarrow{j}+14\overrightarrow{j}\) మరియు \(\overrightarrow{Q}=4\overrightarrow{i}+4\overrightarrow{j}+10\overrightarrow{j}\) అయిన P + Q పరిమాణం కనుక్కోండి. [Imp.Q]
జవాబు:

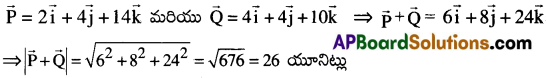
ప్రశ్న 7.
శూన్య పరిమాణం కలిగిన సదిశకు శూన్యం కాని అంశాలు ఉంటాయా?
జవాబు:
ఉండవు. శూన్య పరిమాణం గల ఒక సదిశ శూన్యేతర అంశాలు కలిగి ఉండదు.

ప్రశ్న 8.
ప్రక్షేపకం యొక్క ప్రక్షేప పథం అగ్రభాగంలో దాని త్వరణం ఎంత? [AP, TS 19]
జవాబు:
ప్రక్షేపకం యొక్క పధంలో శిఖరం వద్ద దాని త్వరణం గురుత్వ త్వరణం (g) 9.8ms^-2.

ప్రశ్న 9.
రెండు అసమ పరిమాణం ఉన్న సదిశల సంకలనం మొత్తం శూన్య సదిశను ఇవ్వగలదా? మూడు అసమాన సదిశలు కలిసి శూన్య సదిశను ఇవ్వగలవా?
జవాబు:
కాదు. రెండు అసమాన పరిమాణం గల సదిశలను సంకలనం చేసినపుడు అది శూన్యసదిశను ఇవ్వదు. కాని ఆ మూడు సదిశలు ఒకే తలంలో ఉండి, వానితో ఒక త్రిభుజము నిర్మించగల్గితే, ఆ అసమ సదిశల మొత్తం శూన్యమవుతుంది.

Short Answer Questions (స్వల్ప సమాధాన ప్రశ్నలు)

ప్రశ్న 1.
సదిశల సమాంతర చతుర్భుజ నియమాన్ని పేర్కొనండి. ఫలిత సదిశ పరిమాణం, దిశలకు సమీకరణం రాబట్టండి. [AP 20,22] [TS 16,17,20,22]
జవాబు:
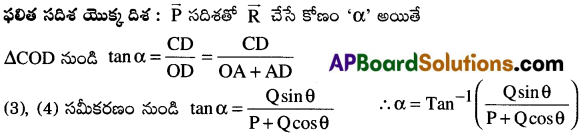
సమాంతర చతుర్భుజ నియమం: రెండు సదిశలను పరిమాణంలోను, దిశలోను ఒక బిందువు నుంచి గీసిన సమాంతర చతుర్భుజం యొక్క రెండు ఆసన్న భుజాలతో సూచిస్తే, ఆ బిందువు గుండా పోయే కర్ణం, పరిమాణంలోను, దిశలోను ఆ రెండు సదిశల ఫలిత సదిశను సూచిస్తుంది.

వివరణ :
పటములో సూచించిన విధముగా, ‘O’ అనే ఒక ఉమ్మడి

ఫలిత సదిశ \(\overrightarrow{R}\) యొక్క పరిమాణం :
లంబకోణ త్రిభుజం ∆COD, నుండి OC² = OD² + CD²
⇒ OC² = (OA + AD)² + CD² (Since, OD = OA + AD)
⇒ OC² = OA² + AD² + 20A. AD + CD² ⇒ OC² = OA² + (AD² + CD²) + 20A.AD ……(1)

ప్రశ్న 2.
సాపేక్ష చలనం అంటే ఏమిటి? వివరించండి.
జవాబు:
సాపేక్షవేగము :
ఒక వస్తువు వేగంతో పోల్చినపుడు మరొక వస్తువు వేగాన్ని ఆ రెండింటి మధ్యగల సాపేక్ష వేగం అంటారు.
A, B అనే రెండు వస్తువులు V_A మరియు V_B వేగాలు కలిగియున్నాయనుకొనుము.

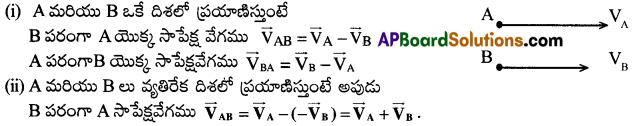
ప్రశ్న 3.
ఒక పడవ నదిని కనిష్ఠ కాలంలో దాటడానికి, ప్రవాహ దిశకు 90° ల కోణంలో ప్రయాణించాలని చూపండి.
జవాబు:
నది ఒక ఒడ్డున A అనే బిందువు వద్ద పడవ బయలుదేరి, పటంలో చూపిన విధంగా రెండో ఒడ్డుకు చేరుకోవాలి.

పై సమీకరణంలో హారం విలువ V_R స్థిరము, (V_b, V_w లు స్థిరము కావున) కావున ‘t’ కనిష్టమవుతున్నపుడు AC కూడా కనిష్టమవుతుంది. AC యొక్క కనిష్ట విలువ AB. ఇది నది వెడల్పు ‘d’కు సమానం. ఇక్కడ V_w కు AB లంబంగా ఉంది. కావున పడవ నదిప్రవాహానికి లంబంగా (90) ల కోణంతో ప్రయాణించవలెను.

ప్రశ్న 4.
శూన్య సదిశ,ఏకాంక సదిశ మరియు స్థాన సదిశలను వివరించండి. [AP 15]
జవాబు:
శూన్య సదిశ (నల్ సదిశ) :
పరిమాణం శూన్యముగా గల సదిశను శూన్య సదిశ అంటారు.
దీనిని \(\overline{\mathrm{0}}\) తో సూచిస్తారు. దాని దిశ అనిశ్చితం.

ఏకాంక సదిశ (లేదా) ప్రమాణ సదిశ :
పరిమాణం ఏకాంకముగా గల సదిశను ఏకాంక సదిశ అంటారు.
ā అనేది శూన్యేతర సదిశ అయితే ā సదిశ దిశలోని ప్రమాణ సదిశను â తో సూచిస్తాము.
ā అనేది శూన్యేతర సదిశ అయితే దాని ఏకాంక సదిశ â = \(\frac{\overline{\mathrm{a}}}{|\bar{a}|}\)

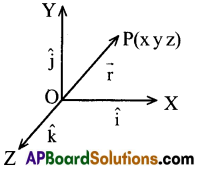
స్థాన సదిశ :
O ఒక నిర్ధేశిత బిందువు, P అంతరాళంలో ఒక బిందువైతే సదిశ \(\overline{\mathrm{OP}}\) ను O బిందువు పరంగా P యొక్క స్థానసదిశ అంటారు.

‘P’ అనే బిందువు యొక్క నిరూపకాలు (x,y,z) మరియు ‘O’ అనునది నిరూపక జ్యామితి యొక్క మూల బిందువు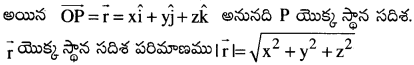

ప్రశ్న 5.
\(|\overrightarrow{\mathbf{a}}+\overrightarrow{\mathbf{b}}|=|\overrightarrow{\mathbf{a}}-\overrightarrow{\mathbf{b}}|\) అయితే \(\overrightarrow{a}\) మరియు \(\overrightarrow{b}\) ల మధ్య కోణం 90° అని నిరూపించండి ? [Imp.Q] [AP 19][TS 18,22]
జవాబు:

ప్రశ్న 6.
క్షితిజ సమాంతర దిశకు కొంత కోణం చేస్తూ విసిరిన వస్తువు (ప్రక్షిప్త) పథం పరావలయం అని చూపండి. [Imp.Q][IPE’ 13, 14][AP 15, 16, 17, 18][TS 15, 16, 18, 22]
జవాబు:
ప్రక్షేపకం :
ఏదైనా ఒక వస్తువును క్షితిజానికి కొంత కోణం θ తో (θ + 90°) విసిరితే దానిని ప్రక్షేపక వస్తువు అని, ఆ మార్గాన్ని ప్రక్షేపక మార్గం అని అంటారు.
ఉదా : క్రికెట్ ఆటలో బాట్స్మన్ కొట్టిన సిక్సర్.

ప్రక్షేపక వస్తువు పథం పరావలయం :
ఒక వస్తువును ‘u’ తొలివేగంతో బిందువునుండి క్షితిజానికి కొంతకోణంతో ప్రక్షిప్తం చేసారనుకొందాము. అప్రక్షేపక వస్తువు వేగం ‘u’ రెండు అంశాలుగా విభజింపబడును.

క్షితిజ సమాంతరాంశం u_x = ucosθ, క్షితిజ లంబాంశం u_y = usinθ

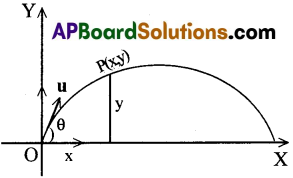
t కాలంలోప్రక్షేపక వస్తువు ప్రయాణించిన
క్షితిజ సమాంతర స్థాన భ్రంశం
x : క్షితిజ సమాంతర వేగం × కాలం = ucosθ x t

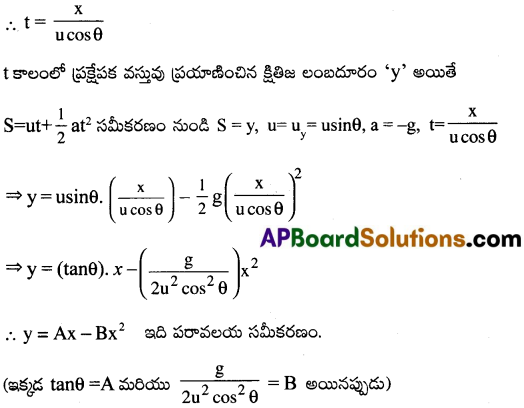
కావున ప్రక్షేపక వస్తుపథం పరావలయం అవుతుంది.

ప్రశ్న 7.
సగటు వేగము, తక్షణ వేగములను వివరించండి. అవి ఎప్పుడు సమానమగును? [AP 19]
జవాబు:
సగటు వేగము :
“మొత్తం స్థానభ్రంశం” మరియు “మొత్తం ప్రయాణించిన కాలము” ల నిష్పత్తిని సగటు వేగం అంటారు. ఒక వస్తువు ‘t’ కాలంలో పొందిన స్థానభ్రంశం ‘s’ అయితే దాని సగటు వేగం = \(\frac{s}{t}\) అవుతుంది.

తక్షణ వేగము :
వస్తువు ప్రయాణించుచున్నపుడు, ఏ క్షణంలోనైనా వస్తువుకు ఉండే వేగాన్ని తక్షణ వేగం అని అంటారు. ఉదా: మోటార్ సైకిల్ యొక్క స్పీడోమీటరు తక్షణ వేగం యొక్క పరిమాణమును సూచించును.
∆t కాల వ్యవధిలో వస్తువు స్థానభ్రంశం ∆s అయితే దాని తక్షణ వేగం

వస్తువు సమవేగంతో ప్రయాణించుచున్నపుడు సగటు వేగం, తక్షణ వేగం సమానమగును.

ప్రశ్న 8.
ప్రక్షిప్తం చేసిన వస్తువు యొక్క గరిష్టోన్నతి మరియు వ్యాప్తికి సమీకరణాలు \(\frac{\mathbf{u}^2 \sin ^2 \theta}{2 g}, \frac{u^2 \sin 2 \theta}{g}\) రాబట్టండి. [Imp.Q]
జవాబు:
గరిష్టోన్నతి :
ప్రక్షిప్త వస్తువు క్షితిజ లంబ వేగాంశం శూన్యం అయ్యేవరకు అది ఊర్ధ్వ దిశలో క్షితిజ లంబంగా చేరుకోగల ఎత్తును దాని గరిష్టోన్నతి అంటారు.
ఒక వస్తువును ‘u’ తొలివేగంతో క్షితిజ సమాంతరానికి ‘θ’ కోణంతో ప్రక్షిప్తం చేసినారు.
తొలివేగాంశం u = usinθ
గరిష్టోన్నతి వద్ద తుదివేగం v = 0
త్వరణం a = −g.
చలన సమీకరణం v² – u² = 2as నుండి 0 – (usinθ)² = -2gh_max

ప్రశ్న 9.
ఒక నిర్దేశ చట్రంలో వస్తువు ప్రక్షిప్త పథం పరావలయం అయితే, ఈ నిర్దేశ చట్రంతో సాపేక్షంగా స్థిరవేగంతో కదులుతున్న మరొక నిర్ధేశ చట్రంలో కూడా వస్తువు పథం పరావలయ ఆకృతిలో ఉంటుందా? ఒకవేళ ప్రక్షేపక పథం పరావలయం కాకపోతే అది ఏ ఆకృతిలో ఉంటుంది?
జవాబు:
మొదటి నిర్దేశ చట్రములో వస్తువు క్షితిజ సమాంతర వేగమునకు సమానమైన వేగముతో దానికి సమాంతరముగా రెండవ నిర్దేశ చట్రము ప్రయాణించుచున్నదనుకొనుము. అపుడు సమాన కాల వ్యవధులలో క్షితిజ సమాంతర దిశలో అవి ప్రయాణించిన దూరములు సమానముగా ఉండును. కనుక వస్తువు క్షితిజ సమాంతరముగా ప్రయాణించలేదు అన్న భావన రెండవ నిర్దేశ చట్రము లోని వ్యక్తికి కలుగును. కాని వస్తువు నిట్ట నిలువు తలములో పైకి పోయి క్రిందికి వచ్చినట్లుగా (అనగా నిట్టనిలువుగా పైకి విసిరిన వస్తువు వలె) అనిపించును.

ప్రశ్న 10.
విరామ స్థితిలో గల వస్తువు పై \(2\overrightarrow{i}+\overrightarrow{j}-\overrightarrow{j}\) న్యూటను బలము పని చేయుచున్నది. 20 సెకనుల తరువాత ఆ వస్తువు వేగం \(4\overrightarrow{i}+2\overrightarrow{j}-2\overrightarrow{j}\)ms^-1. అయిన ఆ వస్తువు ద్రవ్యరాశి ఎంత?
జవాబు:

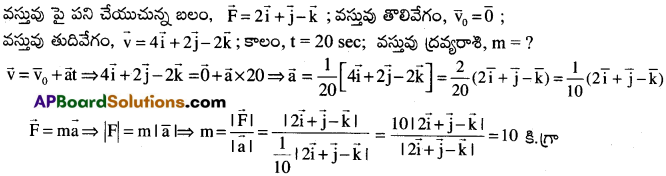
Solved Problems (సాధించిన సమస్యలు)

ప్రశ్న 1.
నిలువుగా క్రింది దిశలో వాన 35 మీ. సె^-1 వేగంతో కురియుచున్నది. కొంత సేపటికి గాలి 12 మీ. సె^-1 వేగంతో తూర్పు నుండి పడమర దిశలో వీచుట ఆరంభించినది. అయిన ఒక పిల్లవాడు వానలో తడవకుండ ఉండుటకు ఏ దిశలో గొడుగు పట్టుకొని ఉండవలయును. [TS 15]
సాధన:

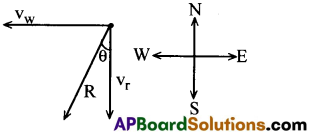
వాన వేగము v_r తోను, గాలి వేగమును v_w తో సూచించిన R
వాని ఫలిత దిశను సూచించును.

కనుక పిల్లవాడు నిలువు తలములో నిట్ట నిలువు క్రింది దిశకు 19° కోణముతో (తూర్పుదిశకు గొడుగు పట్టు కొనవలయును.

ప్రశ్న 2.
నిలువుగా క్రింది దిశలో 35ms వేగంతో వాన కురియుచున్నది. ఒక స్త్రీ తూర్పు నుండి పడమర దిశలో 12ms^-1 వేగంతో సైకిలు తొక్కుచున్నది. ఆమె తడవకుండ ఉండుటకు గొడుగును ఏ దిశలో పట్టుకొనవలయును. [Imp.Q]
సాధన:
వాన వేగం v_r, సైకిల్ వేగం v_b. నేలతో పోల్చినపుడు వాన వేగం, v_r = 35 మీ/సె. నేలతో పోల్చినపుడు సైకిల్ వేగం, v_b = 12 మీ/సె సైకిల్ (స్త్రీ) తో పోల్చినపుడు వాన వేగం v_rb = v_r – v_b.

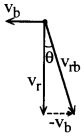
v_rb దిశలో వాన కురియుచున్నట్లుగా ఆమెకు అనిపించును. అందువలన ఆ దిశలో గొడుగు పట్టుకున్నచో ఆమె తడవదు. v_rb నిలువుగా క్రింది దిశకు θ కోణం చేయుచున్నది అని అనుకున్నచో
tan θ = \(\frac{v_b}{v_r}=\frac{12}{35}\) = 0.343 ⇒ θ = Tan^-1(0.343) = 19°
అనగా నిలువుగా క్రింది దిశకు పడమర వైపుగా 19° కోణంతో ఆమె గొడుగును పట్టుకొనవలయును.

ప్రశ్న 3.
ఒక కణము యొక్క స్థానమును సూచించు సమీకరణము r = \(3.0t\overline{\mathrm{i}}+2.0t^2\overline{\mathrm{j}}+5.0\overline{\mathrm{k}}\). ఇందులో t కాలమును సూచించును. t సెకనులలోను, మీటర్లలోను ఉన్నవి. (a) v(t) మరియు a(t) లను కనుగొనుము. (b) t = 1.0సె వద్ద కణము యొక్క వేగం v(t) పరిమాణము, దిశను కనుగొనుము.
సాధన:

ప్రశ్న 4.
45° కోణమునకు సమానముగా ఎక్కువ లేక తక్కువగా ఉన్న ప్రక్షిప్త కోణములకు వ్యాప్తులు సమానమని చూపుము.
సాధన:
ఒక ప్రక్షేపకుమును v₀ వేగముతో క్షితిజ సమాంతర దిశకు θ₀ కోణముతో ప్రక్షిప్తం చేసిన దాని వ్యాప్తి
అనగా R = \(\frac{v_0^2 \sin \left(2 \theta_0\right)}{\mathrm{g}}\)
θ₀ = (45° + α) లేక (45° – α) అయినపుడు 2θ₀ = (90° + 2α) లేక (90° – 2α) అగును.
sin(90° + 2α) = cos2α మరియు sin(90° – 2α) = cos2α
అనగా R విలువ (45° + α), (45° – α) ప్రక్షిప్త కోణములకు సమానం.
కావున 45° కి ఇరువైపులా సమాన స్థాయిలో ఎక్కువ లేదా తక్కువ ఉన్నతాంశాల వ్యాప్తి సమానం.

ప్రశ్న 5.
క్షితిజ సమాంతరమునకు 30° కోణముతో ఒక వస్తువును 28 మీ/సె. వేగంతో ప్రక్షిప్తము చేసిరి. (a) వస్తువు గరిష్టోన్నతిని (b) వస్తువు మరల క్షితిజ సమాంతర తలము వచ్చుటకు పట్టుకాలమును (c) విసిరిన బిందువు నుండి వస్తువు క్షితిజ సమాంతర తలమును తాకిన బిందువు వరకు గల దూరమును (వ్యాప్తి) కనుగొనుము.
సాధన:

Exercise Problems

ప్రశ్న 1.
ఓడ A, ఓడ B నకు పడమటి వైపున 10 కి.మీ దూరంలో ఉన్నది. ఓడ A ఉత్తర దిశలో 30 కి.మీ/గం. వేగంతో ప్రయాణించుచున్నది. ఓడ B ఉత్తరము నుండి పడమర వైపునకు 60° చేయు దిశలో 20 కి.మీ/గం. వేగంతో, ప్రయాణించుచున్నది.
(i) ఓడ Aతో పోల్చిన ఓడ B యొక్క వేగ పరిమాణమును, దిశను
(ii) ఒక దానినొకటి సమీపించు కనిష్ట దూరమును కనుక్కోండి.
సాధన:
A, B లు X- అక్షము పై పటములో చూపినట్లు 10 కి.మీ దూరములో ఉన్నవనుకొనుము.

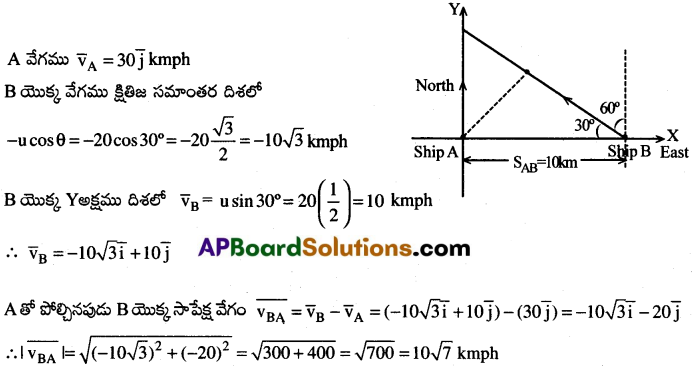
A తో పోల్చినపుడు B యొక్క సాపేక్ష వేగం అనగా A విరామ స్థితిలో ఉన్నదనుకుంటే B యొక్క వేగము.

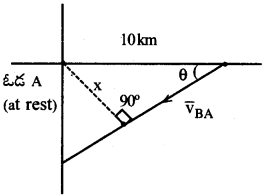
A నుండి సాపేక్ష వేగదిశకు గీచిన లంబము పొడవు అవి ఒకదానికొకటి సమీపించు కనిష్ట దూరమునకు సమానం. పటము నుండి, కనిష్ట దూరం,

ప్రశ్న 2.
ప్రక్షిప్త కోణం θ వ్యాప్తి R, గరిష్ట ఎత్తు h, గమన కాలం T అయితే (a) tanθ = \(\frac{4h}{R}\) (b) = \(\frac{gT^2}{8}\) అని చూపండి.
సాధన:

ప్రశ్న 3.
క్షితిజ సమాంతరంతో 60° కోణం చేస్తూ 800మీ/సె తొలి వేగంతో ఒక ప్రక్షేపకాన్ని పేల్చారు.
(i) భూమిని తాకే ముందు ప్రక్షేపకం ప్రయాణ కాలం కనుక్కోండి.
(ii) అది భూమిని తాకే ముందు ప్రయాణించిన దూరాన్ని (వ్యాప్తి)ని కనుక్కోండి. (iii) గరిష్ఠ ఎత్తుకు చేరుకోవడానికి పట్టే ప్రయాణ కాలాన్ని కనుక్కోండి.
సాధన:
ప్రక్షిప్త కోణం, θ = 60°
ప్రక్షిప్త వేగం, u 800 మీ^-1.

ప్రశ్న 4.
నేలపై ఒక బిందువు నుండి ఒక వస్తువును క్షితిజ సమాంతర దిశకు కొంత కోణముతో ప్రక్షిప్తము చేసిరి. వస్తువు గరిష్ట ఎత్తును చేరినపుడు దాని స్థాన సదిశ పరిమాణము (ప్రక్షిప్త బిందువు మూల బిందువుగా తీసుకున్నపుడు) గరిప్టోన్నతికి √2 రెట్లు ఉన్న ప్రక్షిప్త కోణం Tan^-1(2) అని చూపండి.
సాధన:
గరిష్ట ఎత్తు P వద్ద ఉన్నదనుకొనుము. P బిందువు నిరూపకములు (R/2, h) అవుతాయి.

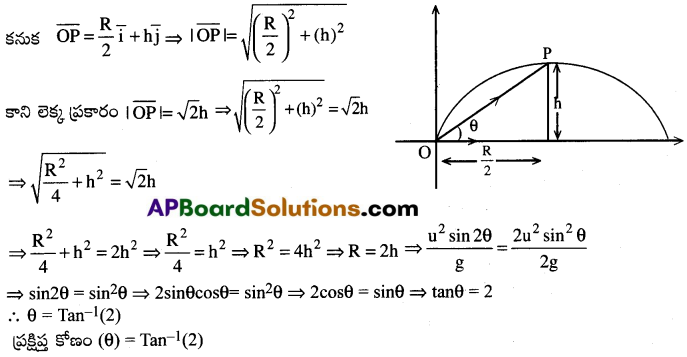
ప్రశ్న 5.
నేల పై నుండి 20 మీ. ఎత్తులో గల శిఖరం నుండి క్షితిజ సమాంతర దిశకు 30° కోణంతో ఒక వస్తువును 30 మీ/ సె. వేగంతో ప్రక్షిప్తం చేసిన నేలను తాకు లోపల అది క్షితిజ సమాంతరముగా ప్రయాణించు దూరం ఎంత? (g = 10 m/s²)
సాధన:
క్షితిజ సమాంతరముగా ప్రయాణించిన మొత్తం దూరం, R = R₁ + R₂.

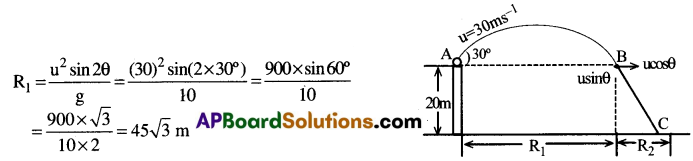
B బిందువు వద్ద క్షితిజ లంబ వేగము (u) = usinθ = 30 × sin30° = 30 × \(\frac{1}{2}\) = 15 ms^-1
త్వరణం (a) = g = 10 మీసె^-2; ప్రయాణించిన దూరం (s) = 20 మీ, కాలం (t) = ?
s = ut + \(\frac{1}{2}\)at² ⇒ 20 = 15 × t + \(\frac{1}{2}\) × 10 × t² ⇒ 20 = 15t + 5t² ⇒ 5t² + 15t – 20 = 0
⇒ t² + 3t-4 = 0 ⇒ t² + 4t – t – 4 = 0 ⇒ t(t+4)-1(t+4) = 0
⇒ (t + 4)(t – 1) = 0 = t = 1s (t = -4 కాలం ఋణాత్మకం కాదు కాబట్టి) t = 1s
1 సెకనులో క్షితిజ సమాంతర దిశలో ప్రయాణించిన దూరం,
R₂ = ucosθ × t = 30 cos30° × 1 = 30 × \(\frac{\sqrt3}{2}\) = 15√3m
∴ మొత్తం క్షితిజ సమాంతర దూరం R = R₁ + R₂ = 45√3 + 15√3 = 60√3 m

ప్రశ్న 6.
నేల పై O అను బిందువు మూల బిందువు ఒక వస్తువు 0 నుండి మొదటి ఈశాన్యదిశలో 10√2m స్థానభ్రంశమును, తరువాత ఉత్తర దిశలో 10 మీ, చివరకు వాయవ్య దిశలో 10√2m స్థానభ్రంశము పొందిన చిట్ట చివరకు వస్తువు మూల బిందువు నుండి ఏ దిశలో, ఎంత దూరములో ఉన్నది. [TS 19]
సాధన:

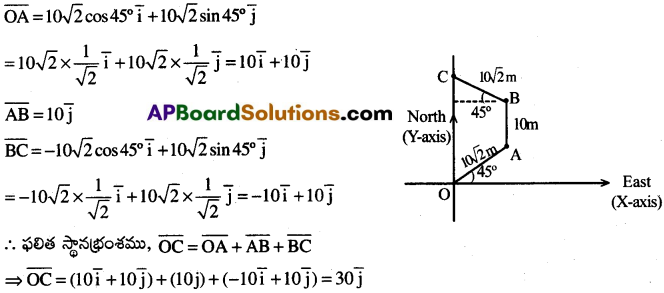
∴ కాబట్టి O నుండి ఉత్తర దిశలో 30మీ దూరములో వస్తువు ఉన్నది.

ప్రశ్న 7.
ఒక వస్తువును నేల పై నుండి వేగంతో వ్యాప్తి గరిష్టముగా ఉండు రీతిలో ప్రక్షిప్తం చేసిరి. గరిష్టాన్నతిని చేరు లోపల వస్తువు సగటు వేగం ఎంత? అనగా ఆరోహణ కాలంలో దాని సగటు వేగం ఎంత?
సాధన:
గరిష్ట వ్యాప్తికి, ప్రక్షిప్త కోణం= 45°.

ప్రశ్న 8.
క్షితిజ సమాంతర దిశకు 45° కోణంతో ఒక వస్తువును కొంత వేగంతో ప్రక్షిప్తం చేసిరి. ప్రక్షిప్త బిందువు నుండి క్షితిజ సమాంతర దిశలో 10 మీ. దూరం ప్రయాణించునప్పటికి, క్షితిజ లంబదిశలో అది 7.5 మీ ఎత్తులో ఉన్నది. దాని ప్రక్షిప్త వేగం ఎంత? (g=10m/s2).
సాధన:
ప్రక్షిప్త వేగము u అనుకొనుము
క్షితిజ సమాంతర దిశలో 10మీ. దూరము ప్రయాణించుటకు పట్టిన కాలం t అనుకొనుము.
కాని క్షితిజ సమాంతర దిశలో ప్రయాణించిన దూరం = క్షితిజ సమాంతర వేగాంశం × కాలం

ప్రశ్న 9.
గాలి దక్షిణం వైపు నుండి 5 మీ/సె. వేగంతో వీచుచున్నది. సైకిల్ పై వెళ్ళుచున్న వ్యక్తికి ఆ వాన తూర్పు నుండి 5 మీ/సె వేగంతో వీచుచున్నట్లు అనిపించిన ఆ వ్యక్తి సైకిల్ పై ఈశాన్యదిశలో 5/2 మీ/సె. వేగంతో వెళ్ళుచున్నాడని చూపండి.
సాధన:

ప్రశ్న 10.
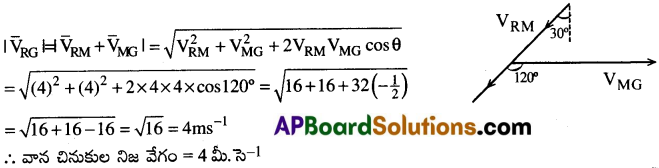
నేలపై 4 మీ/సె వేగంతో నడుచుచున్న వ్యక్తికి వర్షపు బిందువులు క్షితిజ లంబదిశకు 30° కోణంతో అతని ముఖం పై 4 మీ/సె. వేగంతో తాకుచున్నట్లు అనిపించిన వర్షపు బిందువుల నిజ వేగం 4 మీ/సె అని చూపండి.
సాధన:
వ్యక్తితో పోల్చిన వాన వేగం = V_RM = 4 మీసె^-1
నేలతో పోల్చిన వ్యక్తి వేగం = V_MG = 4 మీసె^-1
నేలతో పోల్చిన వాన వేగం = V_RG = ?
(వాన నిజ వేగం)