AP Inter 1st Year Physics Important Questions Chapter 2 Units and Measurements

Students get through AP Inter 1st Year Physics Important Questions 2nd Lesson Units and Measurements which are most likely to be asked in the exam.

AP Inter 1st Year Physics Important Questions 2nd Lesson Units and Measurements

Very Short Answer Questions

Question 1.
Distinguish between Accuracy and Precision. [Mar 13, May 13, 11; AP, TS 15, 16,18]
Answer:

Accuracy	Precision
1) Accuracy denotes how close by a quantity can be measured near to the True value.	1) Precision denotes how precisely (sharply) a quantity can be measured.
2) It varies with Errors in the measurements	2) It varies with least count of the measuring instruments

Question 2.
What are the different types of errors that can occur in a measurement?
Answer:
Types of Errors:

1. Systematic errors
2. Random errors

Systematic errors are further classified as:
(a) Instrumental errors
(b) Personal errors
(c) Imperfection in experimental technique.

Question 3.
How can systematic errors be minimised or eliminated? [IPE’ 14; AP,TS 17]
Answer:
The Systematic errors can be minimized by

1. selecting ‘better instruments’ with ‘higher resolution’
2. avoiding personal bias in taking reading.
3. improving the ’experimental techniques’.

Question 4.
Illustrate how the result of a measurement is to be reported indicating the error involved.
Answer:
1) Suppose the values obtained in several measurements of a quantity are a₁, a₂, a₃, …..a_n.
Calculate their arithmetic mean amean as follows:

2) Now Calculate absolute errors in the measurements as shown below|
|∆a₁| = |a_mean – a₁|, |∆a₂| = |a_mean – a₂|,……|∆a_n| = |a_mean – a_n|
3) Next find mean absolute error as follows:

The final result of measuring the physical quantity is given in the form ∆a_mean =(a_mean ± ∆a_mean)

Question 5.
What are significant figures and what do they represent when reporting the result of a measurement? [TS 18]
Answer:
Significant figures:
The digits of a number that are ‘known reliably’, plus ‘one uncertain digit’, are called “significant figures”.
The significant figures indicate the precision of measurement.

Question 6.
Distinguish between fundamental units and derived units. [IPE’ 14; TS 16,22]
Answer:

Fundamental Units	Derived Units
1) The units of the fundamental quantities are called fundamental units. Ex: metre, kilogram, second.	1) The units of the derived quantities are called derived units. Ex: ms-1, newton.
2) There are 7 fundamental quantities and hence 7 types of fundamental units exist.	2) There are several derived quantities and hence several derived units exist.

Question 7.
Why do we have different units for the same physical quantity? [TS 15, 16, 22]
Answer:
A physical quantity possesses a wide range of magnitudes.

For example, Mass ranges from 10^-30 kg (for an electron) to 10⁵³ kg (for the known universe). Hence, we need different units for different ranges of the same physical quantity.
Ex: mg, gm, kg etc., for mass ; mm, cm, m, km for length

Question 8.
What is dimensional analysis?
Answer:
Dimensional analysis is the process of analysing a physical problem with the help of dimensional equations.

Question 9.
How many orders of magnitude greater is the radius of the atom as compared to that of the nucleus?
Answer:
Radius of atom is of the order of 10^-10 m
Radius of nucleus is of the order of 10^-4 m
So radius of atom is 10⁴ times greater than that of nucleus.
Hence Radius of atom is 4 orders greater than that of nucleus.

Question 10.
Express unified atomic mass unit in Kg. [TS 19, 22]
Answer:
1 unified atomic unit (u) = 1.67 × 10^-27 kg

Short Answer Questions

Question 1.
The vernier scale of an instrument has 50 divisions which coincide with 49 main scale divisions. If each main scale division is 0.5mm, then using this instrument what would be the minimum inaccuracy in the measurement of distance?
Answer:
Minimum inaccuracy = least count of vernier callipers

Question 2.
In a system of units, the unit of force is 100N, unit of length is 10m and the unit of time is 100s. What is the unit of mass in this system?
Answer:

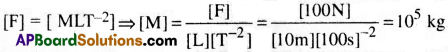
Question 3.
The distance of a galaxy from Earth is of the order of 10²⁵m. Calculate the order of magnitude of the time taken by light to reach us from the galaxy.
Answer:

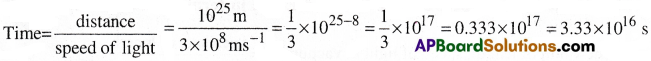
∴ The time taken by light to reach us from the galaxy is in the order of 1016 s with order of magnitude 16 (As 3.33 lies between 0 and 10)

Question 4.
The Earth-Moon distance is about 6(1 Earth radius. What will be the approximate diameter of the Earth as seen from the Moon?
Answer:
Imagine 2R_E as the arc of a circle of radius 60R_E.
Then length of arc = radius x angle subtended by the arc in radians.
⇒ 2R_E = 60 R_E × θ

Question 5.
Three measurements of the time for 20 oscillations of a pendulum give t₁ = 39.6s, t₂ = 39.9s and t₃ = 39.5s. What is the precision in the measurements? What is the accuracy of the measurements?
Answer:
The precision denotes upto what resolution (number of decimal places) the quantity can be measured using the given instrument.

From the given measurements , it is clear that the precision is the least count of watch i.e., 0.1 s
Average time for the 3 measurements = \(\frac{39.6+39.9+39.5}{3}\) = 39.66 s = 39.7 s
Accuracy is the closeness of measured value with true value.
Hence 39.6 s is the accurate of the given 3 measurements.

Question 6.
1 calorie = 4.2 J where 1J = 1 m²s^-2. Suppose we employ a system of units of mass is a kg, the unit of length is \(\hat{a}\) m and the unit of time is \(\hat{a}\) s. Show that a calorie has a magnitude 4.2 \(\dot{a}^{-1} \hat{\mathrm{a}}^{-2} \tilde{\mathrm{a}}^2\) in the new system.
Answer:
Calorie is unit of heat energy. The dimensional formula for energy is ML²T^-2

In S.I system:	New’ system:
Unit of mass, [M1] = 1kg	Unit of mass, [M2] = \(\dot{a}\) kg
Unit of length, [L1] = lm	Unit of length, [L2] = \(\hat{\mathrm{a}}\) m
Unit of time, [T1] = 1 s	Unit of time, [T2] = \(\tilde{\mathrm{a}}\)s
Numerical value, n1 = 4.2	Numerical value, n2 = ?

Question 7.
A new unit of length is chosen so that the speed of light in vacuum is 1 new unit of length /see. If light takes 8 min and 20 s to cover the distance between Sun and Earth, what is the distance between the Sun and Earth in terms of the new unit?
Answer:

Question 8.
A student measures the thickness of a human hair using a microscope of magnification 100. He makes 20 observations and finds that the average thickness (as viewed in the microscope) is 3.5mm. What is the estimate of the thickness of hair?
Answer:

Question 9.
A physical quantity X is related to four measurable quantities a,b,c and d as follows: x = a² b³c^5/2d^-2. The percentage error in the measurement of a, b, c and d are 1%, 2%, 3% and 4% respectively. What is the percentage error in X?
Answer:
Given x = a² b³c^5/2d^-2

Question 10.
The velocity of a body is given by v = At² + Bt + C. If v and t are expressed in Si what are the units of A, B and C?
Answer:
From the principle of homogeneity of dimensions, the units of V, At², Bt, C are equal.
∴ SI unit of At² = SI unit of V ⇒ A s² = m/s ⇒ unit of A = m/s³
SI unit of Bt = SI unit of V ⇒ Bs = m/s ⇒ unit of B = m/s²
SI unit of C = SI unit of V ⇒ unit of C = m/s

Solved Problems

Question 1.
The moon is observed from two diametrically opposite points A and B on Earth. The angle G subtended at the moon by the two directions of observation is 1°54′. Given, the diameter of the Earth to be about 1.276 × 10⁷ m. Compute the distance of the moon from the Earth.

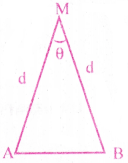
Solution:
We have θ = 1°54′ = 60′ + 54′ = 114′ [∵ 1° = 60′]
= (114 × 60)” × (4.85 × 10^-6) rad [∵ 1″ = 4.85 × 10^-6 rad]
Given that AB = 1.276 × 10⁷m
We have AB = (d)(θ) [∵ Arc length= Radius × Angle]

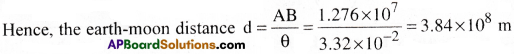
Question 2.
The Sun’s angular diameter is measured to be 1920″. The distance d of the Sun from the Earth is 1.496 × 10¹¹ m. What is the diameter of the Sun?

Solution:
Sun’s angular diameter α = 1920″
= 1920 × 4.85 × 10^-6 rad = 9.31 × 10^-3 rad
Sun’s diameter D = (d)(α) [∵ Arc length= Radius × Angle]
= (9.31 × 10^-3) × (1.496 × 10¹¹)m = 1.39 × 10⁹ m

Question 3.
If the size of a nucleus (in the range of 10^-15 to 10^-14 m) is scaled up to the tip of a sharp pin. What roughly is the size of an atom? Assume tip of the pin to be in the range 10^-5m to 10^-4 m.
Solution:
The size of a nucleus is in the range of 10^-15 m and 10^-14m. The tip of a sharp pin is taken to be in the range of 10^-5 m and 10^-4 m. Thus we are scaling up by a factor of 10¹⁰. Ar. atom roughly of size 10^-10 m will be scaled up to a size of lm. Thus a nucleus in an atom is as small in size, the tip of a sharp pin placed at the centre of a sphere of radius about a meter long.

Question 4.
The resistance R = V/I where V = (100 ± 5)V and I = (10 ± 0.2)A. Find the percentage error in R.
Solution:

Relative error in R = 0.07
Percentage error in R = 0.7 × 100 = 7%

Question 5.
The period of oscillation of a simple pendulum is T = 2π\(\sqrt{\frac{L}{g}}\). Measured value of L is 20.0cm known to 1 mm accuracy and time for 100 oscillations of the pendulum is found to be 90s using a wrist watch of Is resolution. What is the accuracy in the determination of g?
Solution:

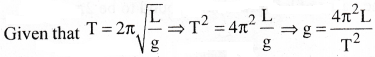
Question 6.
5.74 g of a substance occupies 1.2 cm³. Express its density by keeping the significant figures in view.
Solution:
There are 3 significant figures in the measured mass 5.74 g, whereas there are only 2 significant figures in the measured volume 1.2cm³. Hence the density should be expressed to only 2 significant figures.
Density = \(\frac{5.74}{1.2}\)gcm^-3 = 4.8 gem^-3

Question 7.
Let us consider an equation \(\frac{1}{2}\)mv² = nigh, where m is the mass of the body, v its velocity, g is the acceleration due to gravity and h is the height. Check whether this equation is dimensionally correct. .
Solution:
The dimensions of LHS are [M][LT^-1]² = [M][L²T^-2] = [ML²T^-2]
The dimensions of RHS are [M][LT^-2][L] = [M][L²T^-2] = [ML²T^-2]
The dimensions of LHS and RHS are the same and hence the equation is dimensionally correct.

Question 8.
Consider a simple pendulum, having a bob attached to a string, that oscillates under the action of the force of gravity. Suppose that the period of oscillation of the simple pendulum depends on its length (I), mass of the bob (m) acceleration due to gravity (g). Derive the expression for its time period using method of dimensions.
Solution:
We have T = kl^xg^ym^z. By considering dimensions on both sides, we have
[L°M°T¹] = [L¹]^x[L¹T^-2]^y[M¹]^z = L^x+yT^-2yM^z.
On equating the dimensions on both sides, we have x + y = 0; -2y = 1; z = 0
Hence, x = 1/2, y = -1/2, z = 0.
Then T = kl^1/2 g^-1/2 ⇒ T = k\(\sqrt{\frac{l}{g}}\). The value of k is practically found to be 2π.

Exercise Problems

Question 1.
In the expression P = El²m^-5G^-2 the quantities E, l, m and G denote energy, angular momentum, mass and gravitational constant respectively. Show that P is a dimensionless quantity.
Solution:
The D.F of energy, E is ML²T^-2.
The D.F of angular momentum, l is ML²T^-1.
The D.F of mass, m is M
The D.F of universal gravitational constant, G is M^-1L³T^-2.
ρ = El² m^-5G^-2
= [ML²T^-2] [ML²T^-1]² [M]^-5 [ M^-1L³T^-2 ]^-2
= ML²T^-2 × M²L⁴T^-2 × M^-5 × M²L^-6T⁴ = M^1+2-5+2L^2+4-6T^-2-2+4 = M°L°T°
Hence, P = El²m^-5G^-2 is a dimensionless quantity.

Question 2.
If the velocity of light c, Planck’s constant h and the gravitational constant G are taken as fundamental quantities; express mass, length and time in terms of dimensions of these quantities.
Solution:
Let mass [M] = c^xh^yG^z ⇒ M¹L°T° = [LT^-1]^x [ML²T^-1]^y[M^-1L³T^-2]^z
⇒ M¹L°T° = L^xT^-x × M^yL^2yT^-y × M^-zL^3zT^-2z
⇒ M¹L°T° = M^y-zL^x+2y+3zT^-x-y-2z
y – z = 1 ………. (1); x + 2y + 3z = 0 ……… (2); -x – y – 2z = 0 ………. (3)

Question 3.
An artificial satellite is revolving around a planet of mass M and radius R, in a circular orbit of radius r. Using dimensional analysis show that the period of the satellite T = \({\frac{k}{R}}\sqrt{\frac{r^3}{g}}\) where k is a dimensionless constant and g is acceleration due to gravity.
Solution:
The dependence of time period (T) of satellite on the quantities r, G, and M as a product mass be written as T = kr^aG^bM^c Where k is dimensionless constant By considering dimensions on both sides
[M°L°T¹] = [L]^a [M^-1L3T^-2]^b [M]^c ⇒ [M°L°T¹] = [L]^a [M^-bL^3bT^-2b] [M]^c
⇒ [M°L°T¹]= [M^-b+c L^a+3b T^-2b] on equating dimensions on both sides, we have -b + c = 0,

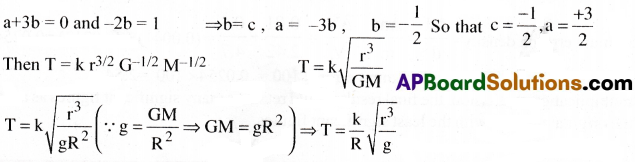
Question 4.
Stale the number of significant figures in the following:
(a) 6729 (b) 0.024 (c) 0.08240 (d) 6.032 (e) 4.57 × 10⁸.
Solution:
(a) 6729: The number of significant figures is 4
Reason: All the non-zero digits are significant

(b) 0.024: The number of significant figures is 2. They are 2 and 4
Reason: If the number is less than 1, the zero(s) on the right of decimal point but to the left of the first non-zero digit are not significant.

(c) 0.08240: The number of significant figures is 4. They are 8,2,4, and 0
Reason: The trailing zero(s) in a number with a decimal point are significant.

(d) 6.032: The number of significant figures is 4. They are 6,0,3 and 2.
Reason: All the zeroes between two non-zero digits are significant, no matter where the decimal point is, if at all.

(e) 4.57 × 10⁸: The number of significant figures is 3. They are 4,5 and 7.
Reason: The power of 10 (here it is 8) is irrelevant to the determination of significant figures.

Question 5.
A stick has a length of 12.132 cm and another has a length of 12.4 cm. If the two sticks are placed end to end what is the total length? If the two sticks are placed side by side, what is the difference in their length?
Solution:
Let l₁ = 12.132 cm and l₂ = 12.4 cm.
Total length when placed end to end = l₁ + l₂ = 12.132 + 12.4 = 24.532 cm = 24.5 cm
When placed side by side, difference in lengths = l₂ – l₁ = 12.4 – 12.132 = 0.268 = 0.3 cm

Reason :
In addition or subtraction, the final result should retain as many decimal places as are there in the number with the least decimal places.

Question 6.
Each side of a cube is measured to be 7.203m. What is (i) the total surface area and (ii) the volume of the cube, to appropriate significant figures?
Solution:
Side of a cube, s=7.203 m
Total surface area of cube, A = 6s² = 6(7.203)² = 6×51.883209 = 311.299254 m² = 311.3 m²
The answer should contain only 4 significant digits as side of the cube has 4 significant figures Volume of the cube, V = s³ = (7.203)3 = 373.7147544m³ = 373.7 m³.

Question 7.
The measured mass and volume of a body are 2.42 g and 4.7 cm³ respectively with possible errors 0.01g and 0.1cm³. Find the maximum error in density.
Solution:
Measured mass, m = 2.42 g
Measured volume, V = 4.7 cm³
Error in mass, ∆m = 0.01 g
Error in volume, ∆V = 0.1 cm³

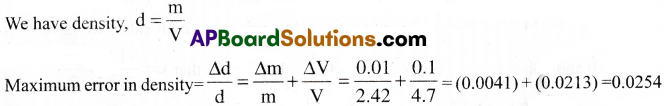
Percentage error in density = Maximum error × 100 = 0.0254 × 100 = 2.54
In multiplication or division, the final result should retain as many significant figures as are there in the original number with the least significant figures.

Question 8.
The error in measurement of radius of a .sphere is 1%. What is the error in the measurement of volume? [AP 19, 19]
Solution:

∴ Error in the measurement of volume is 3%.

Question 9.
The percentage error in the mass and speed are 2% and 3% respectively. What is the maximum error in kinetic energy calculated using these quantities? [TS 20] [AP 18,20]
Solution:

Question 10.
One mole of an ideal gas at standard temperature and pressure occupies 22.4 (molar volume). If the size of the hydrogen molecule is about 1A. What is the ratio of molar volume to the atomic volume of the mole of hydrogen?
Solution:
Diameter of hydrogen molecule = 1Å = 1 × 10^-10 m

Question 11.
Find the relative error in Z if Z = \(\frac{A^4 B^{1 / 3}}{C D^{3 / 2}}\) [TS May 19]
Solution:

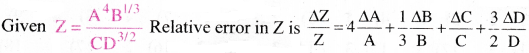
Multiple Choice Questions

1. The S.l unit of Moment of Inertia is
1 ) Kg/m²
2) Kgm²
3) N/m²
4) Nm²
Answer:
2) Kgm²

2. The unit of angular momentum in C.GS system
1) J-s
2) erg-s
3) ergs^-1
4) cals^-1
Answer:
2) erg-s

3. The unit of thermal conductivity is
1) W m^-1 K^-1
2) J m K^-1
3) J m^-1 K^-11
4) W m K^-1
Answer:
W m^-1 K^-1

4. The dimensional formula ML²T^-2 represents
1) Moment of a force
2) Force
3) Acceleration
4) Momentum
Answer:
1) Moment of a force

5. Which of the following has the dimensions of pressure?
1) [MLT^-2]
2) [ML^-1T^-2]
3) [ML^-2T^-1]
4) [M^-1L^-1]
Answer:
2) [ML^-1T^-2]

6. The dimensional formula of torque is
1) [ML²T^-2]
2) [MLT^-2]
3) [ML^-1T^-2]
4) [ML^-2T^-2]
Answer:
1) [ML²T^-2]

7. The dimensional formula for angular velocity is
1) [M^-1L¹T°]
2) [M°L^-1T^-1]
3) [M^-1L^-1T°]
4) [M°L°T^-1]
Answer:
4) [M°L°T^-1]

8. The dimensional formula of angular momentum is
1) [ML²T^-2]
2) [ML^-2T^-1]
3) [MLT^-1]
4) [ML²T^-1]
Answer:
4) [ML²T^-1]

9. Dimensions of stress are
1) [MLT^-2]
2) [ML²T^-2]
3) [ML°T^-2]
4) [ML^-1T^-2]
Answer:
4) [ML^-1T^-2]

10. The dimensions of universal gravitational constant are
1) [M^-1L³T^-2]
2) [ML²T^-1]
3) [M^-2L³T^-2]
4) [M^-2L²T^-1]
Answer:
1) [M^-1L³T^-2]

11. The dimensional formula for latent heat is
1) MLT^-2
2) ML²T²
3) M°L²T^-2
4) MLT^-1
Answer:
3) M°L²T^-2

12. Which one of the following represents the correct dimensions of the coefficient of viscosity?
1) ML^-1T^-2
2) MLT^-1
3) ML^-1T^-1
4) ML^-2T^-2
Answer:
3) ML^-1T^-1

13. The dimensions of (µ₀ε₀)^-1/2 are
1) [L^1/2T^-1/2]
2) [L^-1T]
3) [LT^-1]
4) [L^1/2T^1/2]
Answer:
3) [LT^-1]

14. The dimensions of Planck’s constant equals to that of
1) energy
2) momentum
3) angular momentum
4) power
Answer:
3) angular momentum

15. The ratio of the dimensions of Planck’s constant and that of moment of inertia is the dimensions of
1) time
2) frequency
3) angular momentum
4) velocity
Answer:
2) frequency

16. The dimensions of impulse are equal to that of
1) pressure
2) linear momentum
3) force
4) angular momentum
Answer:
2) linear momentum

17. The pair of quantities having same dimensions is
1) Impulse and Surface Tension
2) Angular momentum and Work
3) Work and Torque
4) Young’s modulus and Energy
Answer:
3) Work and Torque

18. Which pair do not have equal dimensions?
1) Energy and torque
2) Force and impulse
3) Angular momentum and Planck’s constant
4) Elastic modulus and pressure.
Answer:
2) Force and impulse

19. If pressure P, velocity V and time T are taken as fundamental physical quantities, the dimensional formula of the force is
1) PV²T²
2) P^-1V²W^-2
3) PVT^-2
4) P^-1VT^-2
Answer:
1) PV²T²

20. If force (F), velocity (V) and time (T) are taken as fundamental units, then the dimensions of mass are
1) [FVT^-1]
2) [FVT^-2]
3) [FV^-1T^-1]
4) [FV^-1T]
Answer:
4) [FV^-1T]

21. If force [F], acceleration [A] and time [T] are chosen as the fundamental physical quantities. Find the dimensions of energy.
1) [F][A^-1][T]
2) [F][A][T]
3) [F] [A] [T²]
4) [F] [A] [T^-1]
Answer:
3) [F] [A] [T²]

22. If E and G respectively denote energy and gravitational constant, then E/G has the dimensions of
1) [M²][L^-2][T^-1]
2) [M²][L^-1][T°]
3) [M][L^-1][T^-1]
4) [M][L°][T°]
Answer:
2) [M²][L^-1][T°]

23. If the error in the measurement of radius of is 2%, then the error in the determination of of the sphere will be
1) 8%
2) 2%
3) 4%
4) 6%
Answer:
3) 4%

24. Percentage errors in the measurement of mass and speed are 2% and 3% respectively. The error in the estimate of kinetic energy obtained by measuring ma. and speed will be
1) 8%
2) 2%
3) 12%
4) 10%.
Answer:
1) 8%

25. The density of a cube is measured by measuring its mass and length of its sides. If the maximum error in the measurement of mass and lengths are 3% and 2% respectively, the maximum error in the measurement of density would be
1) 12%
2) 14%
3) 7%
4) 9%.
Answer:
4) 9%.

26. In an experiment, the percentage of error occurred in the measurement of physical quantities A, B, C and D are 1%, %, 3% and 4% respectively. Then (lie maximum percentage of error in the measurement X, where X = \(\frac{\mathrm{A}^2 \mathrm{~B}^{1 / 2}}{\mathrm{C}^{1 / 3} \mathrm{D}^3}\), will be
1) 10%
2) (3/13)%
3) 16%
4) -10%
Answer:
3) 16%

27. If the dimensions of a physical quantity are given by M^aL^bT^c, then the physical quantity will be
1) velocity if a = 1, b = 0, c = -1
2) acceleration if a = 1, b = 1, c = -2
3) force if a = 0, b = -1, c = -2
4) pressure if a = 1, b = -1, c = -2
Answer:
4) pressure if a = 1, b = -1, c = -2

28. The damping force on an oscillator is directly proportional to the velocity. The units of the constant of proportionality are
1) kg m s^-1
2) kg m s^-2
3) kg s^-1
4) kg s
Answer:
3) kg s^-1

29. Taking into account of the significant figures, what is the value of 9.99 m – 0.0099 m?
1) 9.9801 in
2) 9.98 m
3) 9.980 m
4) 9.9 m
Answer:
2) 9.98 m

30. A screw gauge has least count of 0.01 mm and there are 50 divisions in its circular scale. The pitch of the screw gauge is
1) 0.01 mm
2) 0.25 mm
3) 0.5 mm
4) 1.0 mm
Answer:
3) 0.5 mm