AP Inter 1st Year Physics Important Questions Chapter 2 ప్రమాణాలు, కొలత

Students get through AP Inter 1st Year Physics Important Questions 2nd Lesson ప్రమాణాలు, కొలత which are most likely to be asked in the exam.

AP Inter 1st Year Physics Important Questions 2nd Lesson ప్రమాణాలు, కొలత

Very Short Answer Questions (అతిస్వల్ప సమాధాన ప్రశ్నలు)

ప్రశ్న 1.
యదార్థత, ఖచ్చితత్వం మధ్య తేడాలు వ్రాయండి. [Mar 13, May 13][AP, TS 15, 16, 17, 18]
జవాబు:

యదార్థత	ఖచ్చితత్వము
1) కొలిచిన విలువకు నిజవిలువ ఎంత దగ్గరగా ఉంటుందో తెలియచేసేదే యదార్థత.	1) వివిధ పరిశీలనలకు సంబంధించిన కొలతలు ఎంత దగ్గరగా ఉంటాయో తెలియచేసేదే ఖచ్చితత్వం.
2) యదార్ధత దోషాలపై ఆధారపడుతుంది.	2) ఖచ్చితత్వము దోషాలపై ఆధారపడదు.
3) యదార్థత అనేది కొలిచే పరికరం అవధి, పృధక్కరణం వంటి విషయాలపై ఆధారపడి ఉండును.	3) ఖచ్చితత్వం అనేది కొలిచే పరికరం పృధక్కరణం పై ఆధారపడి ఉండును.

ప్రశ్న 2.
కొలతలో వచ్చే వివిధ రకములయిన దోషములు ఏవి?
జవాబు:
దోషాల రకాలు (1) క్రమదోషాలు (2) యాదృచ్ఛిక దోషాలు
క్రమదోషాలను మరల ఈ క్రింది విధంగా వర్గీకరించవచ్చును. (a) పరికరం వలన కలిగే దోషాలు (b) వ్యక్తిగత దోషాలు (c) ప్రయోగ పద్ధతిలోని అసమగ్రత వలన కలిగే దోషాలు.

ప్రశ్న 3.
క్రమ దోషాలను ఏ విధంగా కనిష్టము చేయవచ్చును లేక తొలగించవచ్చును? [IPE ’14][AP, TS 17, 18] [AP 22]
జవాబు:
క్రమదోషాలను కనిష్టము చేయు లేదా తొలగించు పద్ధతులు:

1. ప్రయోగ పద్ధతులను అభివృద్ధి చెందించుట మరియు మంచి పరికరములను ఉపయోగించుట
2. వ్యక్తిగత దోషాలను సాధ్యమైనంత వరకు తగ్గించుట
3. ప్రయోగములో సంభవించగల దోషాలను ముందుగా ఊహించి దానికి అనుగుణంగా కొలతలకు తగిన సవరణలు చేయుట

ప్రశ్న 4.
కొలత ఫలితాన్ని అందులో ఉండే దోషాన్ని సూచిస్తూ ఏ విధంగా నివేదిస్తారో ఉదాహరణలతో వివరించండి.
జవాబు:
1) అనేక కొలతల్లో పొందిన విలువలు వరుసగా a₁, a₂, a₃, ….a_n. అనుకొనుము. వాని అంకమధ్యమము a_M ను ఈ క్రింది విధంగా కనుగొనవలయును.
a_mean = \(\frac{a_1+a_2+a_3+…….+a_n}{n}\)

2) కొలతలలోని పరమ దోషములను ఈ క్రింది విధంగా కనుగొనవలయును.
|∆a₁| = |a_mean = a₁|,|∆a₂| = |a_mean – a₂|, …….|∆a_n| = |a_mean – a_n|

3) అన్ని పరమ దోషాల అంకమధ్యమమును కనుగొనవలయును.

భౌతికరాశి యొక్క తుది ఫలితాన్ని ఈ క్రింది విధంగా నివేదించ వలయును ∆a_mean = (a_mean ± ∆a_mean)

ప్రశ్న 5.
సార్థక సంఖ్యలు అనగా ఏమి? ఒక కొలత ఫలితాన్ని నివేదించేటప్పుడు అవి ఏమి సూచిస్తాయి?
జవాబు:
ఒక కొలతను సూచించే సంఖ్యలో నిశ్చయంగా తెలిసిన అంకెలు. వీటికి తోడు అదనంగా, అంచనా ప్రకారం చేర్చిన అంకె, వీటన్నింటినీ కలిపి సార్థక సంఖ్యలు అని అంటారు.

సార్థక సంఖ్యల వలన కొలతలోని ఖచ్చితత్వం తెలియును మరియు కొలతలోని నమ్మదగిన భాగమును సూచించును.

ప్రశ్న 6.
ప్రాథమిక ప్రమాణాలు మరియు ఉత్పన్న ప్రమాణాల మధ్య తేడాలు వ్రాయండి. [IPE’14][TS 22]
జవాబు:

ప్రాథమిక ప్రమాణాలు	ఉత్పన్న ప్రమాణాలు
1. ప్రాథమిక భౌతిక రాశుల ప్రమాణాలను ప్రాథమిక ప్రమాణాలు అని అంటారు. ఉదా: మీటరు, కిలోగ్రాము మొదలైనవి.	1. ఉత్పన్న భౌతిక రాశుల ప్రమాణాలను ఉత్పన్న ప్రమాణాలు అని అంటారు. ఉదా: మీ/సె, న్యూటను
2. ప్రాథమిక భౌతిక రాశులు 7. కావున ప్రాథమిక ప్రమాణాలు పరిమిత సంఖ్యలో ఉండును.	2. ఉత్పన్న రాశులు చాలా సంఖ్యలో ఉండును. కనుక ఉత్పన్న ప్రమాణాలు కూడా చాలా ఉండును.

ప్రశ్న 7.
ఒకే భౌతిక రాశికి వేరువేరు ప్రమాణములు ఎందుకు ఉంటాయి? [Imp.Q][TS 15, 16, 22]
జవాబు:
ఏదైనా ఒక భౌతికరాశి, ఉదాహరణకు ద్రవ్యరాశిని గమనించిన, వస్తువుల ద్రవ్యరాశి చాలా విస్తృత అవధిలో మారుచుండును. ఉదాహరణకు ఎలక్ట్రాను ద్రవ్యరాశి 10^-30 kg క్రమములో ఉండును. విశ్వము ద్రవ్యరాశి 10⁵⁵ kgక్రమములో ఉండును. కనుక ఒక వస్తువు ద్రవ్యరాశిని తెలియజేయుటకు తగిన ప్రమాణమును తీసుకొనవలయును. అనగా వస్తువు ద్రవ్యరాశి చాలా తక్కువగా ఉన్నచో, మిల్లిగ్రాములు లేక గ్రాములలో తెలియజేయవచ్చును. ద్రవ్యరాశి ఎక్కువగా ఉన్నచో కి.గ్రా లేక క్వింటాలులలో తెలియజేయ వచ్చును.

ప్రశ్న 8.
మితీయ విశ్లేషణ అనగా ఏమి?
జవాబు:
మితి సమీకరణాల సహాయముతో భౌతిక శాస్త్రములోని సమస్యలను విశ్లేషించు పద్ధతిని మితీయ విశ్లేషణ అని అంటారు.

ప్రశ్న 9.
కేంద్రకం వ్యాసార్థముతో పోలిస్తే పరమాణు వ్యాసార్థం పరిమాణ క్రమాలలో ఎంత ఎక్కువగా ఉంటుంది?
జవాబు:
పరమాణు వ్యాసార్థం 10^-10 m క్రమములో ఉండును.
కేంద్రకం వ్యాసార్థం 10^-14 m క్రమములో ఉండును.

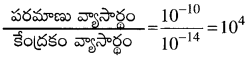
కనుక పరమాణు వ్యాసార్థం, కేంద్రక వ్యాసార్థమునకు 10⁴ రెట్లు ఉండును.
పరమాణు వ్యాసార్థం, పరిమాణ క్రమము, కేంద్రక వ్యాసార్థము పరిమాణ క్రమమునకు 4 రెట్లు ఉండును.

ప్రశ్న 10.
ఏకీకృత పరమాణు ద్రవ్యరాశి ప్రమాణమును కి.గ్రాలలో తెలియజేయుము. [TS 19, 22]
జవాబు:
ఏకీకృత పరమాణు ద్రవ్యరాశి ప్రమాణము (a.m.u) = 1.67 × 10^-27 kg

Short Answer Questions (స్వల్ప సమాధాన ప్రశ్నలు)

ప్రశ్న 1.
ఒక పరికరములోని వెర్నియర్ స్కేలులో 50 విభాగములు ఉన్నవి. అవి 49 ప్రధాన స్కేలు విభాగములకు సమానం. ఒక్కొక్క ప్రధాన స్కేలు విభాగం పొడవు 0.5 మి.మీ. అయిన ఆ పరికరమును ఉపయోగించి కొలచిన పొడవులో వచ్చు కనిష్ట యధార్థతారాహిత్యం ఎంత?
జవాబు:
పొడవులోని కనిష్ఠ యధార్థతారాహిత్యం = పరికరము యొక్క కనీసపు కొలత
వెర్నియర్ స్కేలులోని విభాగముల సంఖ్య = N = 50
ప్రధాన స్కేలు విభాగం పొడవు, S = 0.5 మి.మీ
వెర్నియర్ స్కేలు కనీసపు కొలత, L.C = \(\frac{S}{N}=\frac{0.5mm}{50}\) = 0.01mm

ప్రశ్న 2.
ప్రమాణాల ఒక వ్యవస్థలో బలానికి ప్రమాణం 100N, పొడవుకు ప్రమాణం 10m, కాలానికి ప్రమాణం 100s. ఈ వ్యవస్థలో ద్రవ్యరాశికి ఉండే ప్రమాణం ఏది?
జవాబు:
బలము ప్రమాణం = 100 N; పొడవు ప్రమాణం = 10 m; కాలం ప్రమాణం = 100S; ద్రవ్యరాశి ప్రమాణం =?

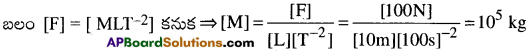
ప్రశ్న 3.
భూమి నుండి ఒక గెలాక్సీ దూరం 10²⁵m క్రమములో ఉన్నది. గెలాక్సీ నుండి కాంతి భూమిని చేరుటకు పట్టే కాలం పరిమాణం క్రమాన్ని గణించండి.
జవాబు:
కాంతి వేగం = 3 × 10⁸ మీ/సె, నక్షత్ర వీధికి, భూమికి మధ్యగల దూరం = 10²⁵ మీ, కాలం (t) = ?
దూరం = వేగం × కాలం కనుక

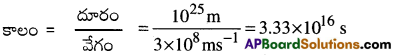
∴ కాల క్రమము = 10¹⁶ సె (3.33 < 5 కనుక కాలక్రమం 10¹⁶ అగును.)

ప్రశ్న 4.
భూమి-చంద్రుల మధ్యగల దూరం సుమారు భూ వ్యాసార్థంనకు 60 రెట్లు. అయిన చంద్రుని నుండి చూస్తే భూమి వ్యాసం సుమారుగా ఎంత ఉండును.
జవాబు:

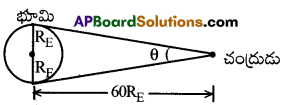
భూమికి, చంద్రునికి మధ్యగల దూరం 60R_E. వ్యాసార్థముగా ఒక వృత్తమును ఊహించుము. భూమి వ్యాసం 2R_E వృత్త చాపము అనుకొనుము. వృత్త చాపం, వృత్త కేంద్రం వద్ద (అనగా చంద్రుని) చేయు కోణం θ అయిన

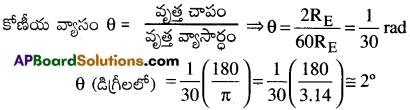
ప్రశ్న 5.
ఒక లోలకము 20 డోలనాలకు పట్టే కాలానికి వచ్చిన మూడు కొలతలు వరుసగా t₁ = 39.6 సెకనులు, t₂ = 39.9 సెకనులు, t₃ =39.5 సెకనులు అయిన ఆ కొలతలలోని (a) ఖచ్చితత్వము ఎంత? (b) యదార్థత ఎంత?
జవాబు:
వివిధ పరిశీలనలకు సంబంధించిన కొలతలు ఎంత దగ్గరగా (దశాంశ స్థానముల సంఖ్య) ఉంటాయో తెలియచేసేదే ఖచ్చితత్వం.
(a) ఇచ్చిన కొలతల నుండి ఖచ్చితత్వం = గడియారము కనీసపు కొలత = 0.1 సె.

(b) 3 కొలతలు పూర్తి చేయుటకు పట్టిన సగటు కాలం = \(\frac{39.6+39.9+39.5}{3}\) = 39.66s = 39.7s
∴ కొలిచిన విలువలకు బాగా దగ్గరగా ఉండునదే యదార్థత
కావున ఇచ్చిన మూడు విలువలలో యదార్థ విలువ 39.6 సె.

ప్రశ్న 6.

జవాబు:
కెలోరి శక్తికి (ఉష్ణశక్తికి) ప్రమాణము. దీని మితి ఫార్ములా ML²T^-2

ప్రశ్న 7.
శూన్యములో కాంతి వడి 1ms^-1 అగునట్లుగా పొడవుకు ఒక క్రొత్త ప్రమాణమును ఎంచుకున్నారు. సూర్యుని నుండి కాంతి భూమిని చేరుటకు పట్టు కాలం 8 నిమిషముల 20 సెకనులు అయిన క్రొత్త ప్రమాణాలలో సూర్యునికి, భూమికి మధ్యగల దూరం ఎంత?
జవాబు:

ప్రశ్న 8.
ఆవర్థనము 100 గల సూక్ష్మదర్శినిని ఉపయోగించి ఒక విద్యార్థి 20 పరిశీలనలు చేసి మానవుని వెంట్రుక సగటు మందము 3.5 మీ.మీ అని కొలిచెను. అయిన అంచనాకు వచ్చే ఆ వెంట్రుక మందము ఎంత ?
జవాబు:

ప్రశ్న 9.
ఒక భౌతిక రాశి X కొలవగల నాలుగు భౌతిక రాశులు a, b, c మరియు d లపై ఈ విధముగా ఆధార పడియున్నది. x = a²b³c^5/2d^-2. a, b, c మరియు d ల లోని దోష శాతములు వరుసగా 1%, 2%, 3% మరియు 4% అయిన X లోని దోష శాతం ఎంత?
జవాబు:
x లోని దోష శాతం = 2 × a లోని దోష శాతం + 3 × b లోని దోష శాతం + \(\frac{5}{2}\) × c లోని దోష శాతం +2 × dలోని దోష శాతం (దోషములన్ని కూడ వలయును)
= 2 × 1% + 3 × 2% + \(\frac{5}{2}\) × 4%
= 2% + 6% + \(\frac{15}{2}\)% + 8%
= 23.5%
= 24%

ప్రశ్న 10.
ఒక వస్తువు వేగము, కాలంతో పాటు V = At² + Bt + C సమీకరణ సూత్ర ప్రకారం మార్పు చెందుతుంది. V, tల ప్రమాణాలు S.I లో ఉంటే A, B,C స్థిరాంకాల ప్రమాణాలు కనుక్కోండి.
జవాబు:
మితుల సజాతీయత సూత్రం ప్రకారం V, At², Bt, C ల ప్రమాణాలు సమానం.
At² యొక్క SI ప్రమాణం = V యొక్క SI ప్రమాణం ⇒ A s² = m/s A యొక్క ప్రమాణం = m/s³
Bt యొక్క SI ప్రమాణం = V యొక్క SI ప్రమాణం ⇒ Bs = m/s ⇒ B యొక్క ప్రమాణం m/s²
C యొక్క SI ప్రమాణం = V యొక్క SI ప్రమాణం ⇒ C యొక్క ప్రమాణం = m/s

Solved Problems (సాధించిన సమస్యలు)

ప్రశ్న 1.
భూమి పై ఏదైన ఒక వ్యాసము యొక్క రెండు చివరి బిందువులు A, B. A, B ల వద్ద నుండి వరుసగా చంద్రుని చూచినపుడు చంద్రుని వద్ద ఆ రెండు పరిశీలన దిశల మధ్య కోణము 1°54′. భూమి వ్యాసము సుమారుగా 1.276 × 10⁷ మీ. అయిన భూమి నుండి చంద్రుని దూరము ఎంత?
సాధన:

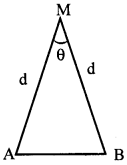
పటములో భూమి వ్యాసము AB = 1.276 × 10⁷మీ
A,B ల వద్ద నుండి చూచినపుడు రెండు పరిశీలన
దిశల మధ్య కోణము θ = 1°54′ = 60′ + 54′ = 114′ [∵ 1° = 60′]
= (114 × 60)” × (4.85 × 10^-6) rad [∵ 1″ = 4.85 × 10^-6 rad]
గణిత శాస్త్ర నియమముల ప్రకారం AB = dθ

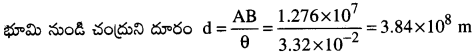
ప్రశ్న 2.
భూమి పై నుంచి చూచినపుడు సూర్యుని కోణీయ వ్యాసము 1920″. భూమి నుండి సూర్యుని దూరం D 1.496 × 10¹¹ m. అయిన సూర్యుని వ్యాసము ఎంత?
సాధన:

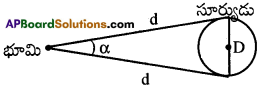
సూర్యుని కోణీయ వ్యాసము α = 1920″
= 1920 × 4.85 × 10^-6 రేడియన్ – 9.31 × 10^-3 రేడియన్
సూర్యుని వ్యాసము D = αd = (9.31 × 10^-3) × (1.496 × 10¹¹)m = 1.39 × 10⁹ మీ

ప్రశ్న 3.
10^-15 నుండి 10^-14 మీ సైజులో ఉండు కేంద్రకమును 10^-5 మీ నుండి 10^-4 మీ. సైజులో ఉండు సూది మొనకు పెంచినట్లు భావించిన సుమారుగా ఒక పరమాణువు సైజు ఎంత ఉన్నట్లు భావించవచ్చును.
సాధన:
10^-15 × 10¹⁰ = 10^-5 లేక 10^-14 × 10¹⁰ = 10^-4
అనగా కేంద్రకము యొక్క సైజును సుమారుగా 10¹⁰ రెట్లు పెంచిరి. అదే విధముగా 10-10 మీ సైజు ఉండు పరమాణువును 1010 రెట్లు పెంచిన 1 మీ అగును. అనగా 1 మీటరు వ్యాసార్థము గల గోళము కేంద్రము వద్ద ఒక గుండు సూది మొన ఎట్లు ఉండునో పరమాణువు కేంద్రము వద్ద కేంద్రకము కూడా అట్లే ఉండును.

ప్రశ్న 4.
నిరోధము R= VII పొటెన్షియల్ తేడా V = (100 ± 5)V మరియు కరెంట్ I = (10 ± 0.2)A. అయిన నిరోధములోని దోష శాతము ఎంత?
సాధన:

ప్రశ్న 5.
ఒక లఘులోలకం ఆవర్తనకాలం T = 2π\(\sqrt{\frac{L}{g}}\) లోలకము యొక్క కొలిచిన పొడవు L= 20.0 సెం.మీ దీనిలోని యదార్థత 1 మి.మీ లోలకము 100 కంపనములు పూర్తిచేయుటకు పట్టు కాలము 90 సెకన్లు అని ఒక గడియారము ద్వారా కొలిచిరి. గడియారము యొక్క పృథక్కరణ (resolution) 1 సెకను. అయిన g విలువను కనుగొన్నపుడు దానిలోని యదార్థత ఎంత?
సాధన:

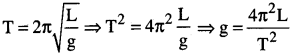
ప్రశ్న 6.
ఒక వస్తువు ద్రవ్యరాశి 5.74 గ్రా. దాని ఘనపరిమాణం 1.2 సెం.మీ³. అయిన సార్థక సంఖ్యలను (significant figures) దృష్టిలో ఉంచుకొని ఆ వస్తువు సాంద్రతను కనుగొనుము.
సాధన:
ద్రవ్యరాశి కొలతలో మూడు సార్థక సంఖ్యలు, ఘనపరిమాణ కొలతలో 2 సార్థక సంఖ్యలు ఉన్నవి. నియమము ప్రకారం సాంద్రత కొలతలో కూడ 2 సార్థక సంఖ్యలు మాత్రమే ఉండవలయును.

ప్రశ్న 7.
\(\frac{1}{2}\)mv² = mgh, అను సమీకరణములో m ద్రవ్యరాశిని, ” వేగమును, g గురుత్వ త్వరణమును, h ఎత్తును సూచించును. ఈ సమీకరణం మితుల ప్రకారం సరియైనదేనా?
సాధన:
\(\frac{1}{2}\)mv² యొక్క మితులు [M][LT-1]² = [M][L²T^-2] = [ML²T^-2]
mgh యొక్క మితులు [M][LT^-2][L] = [M][L²T^-2] = [ML²T^-2]
రెండు వైపుల ఒకే మితులు వచ్చినవి కనుక మితుల ప్రకారం ఇచ్చిన సమీకరణం సరియైనదే.

ప్రశ్న 8.
ఒక లఘులోలకం ఆవర్తన కాలం (T), దాని పొడవు (l) పై లోలకం గుండు ద్రవ్యరాశి (m) పై గురుత్వ త్వరణం (g) పై ఆధారపడి ఉండవచ్చునని భావించి Tకు సమీకరణం ఉత్పాదించండి.
సాధన:
T = kl_xg_ym_z. అని అనుకొనుము
ఇరువైపుల మితిఫార్ములాలు వ్రాయగా
[L₀M₀T¹] =[L¹]_x[L¹T_-2]_y[M1]_z = L_x+yT_-2yM_z.
ఘాతాంకములను పోల్చగా x + y = 0; -2y = 1; z = 0
వీని నుండి, x = 1/2, y = -1/2, z = 0. అని గమనించవచ్చు.
ప్రయోగాత్మకంగా k = 2 అని కనుగొన్నారు.
T = k l^1⁄2 g^-1⁄2 ⇒ T = k\(\sqrt{\frac{l}{g}}\) ⇒ T = 2π\(\sqrt{\frac{l}{g}}\)

Exercise Problems

ప్రశ్న 1.
P = El²m^-5G^-2 నందు E, శక్తిని, 1కోణీయ ద్రవ్యవేగమును, m ద్రవ్యరాశిని, ఆ విశ్వ గురుత్వ స్థిరాంకమును
సూచించిన P కు మితులు ఉండవని నిరూపింపుము.
సాధన:
E కి మితిఫార్ములా ML²T^-2.
l కి మితిఫార్ములా ML²T^-1.
m కి మితిఫార్ములా M
G కి మితిఫార్ములా M^-1L³T^-2.
ఇప్పుడు, El²m^-5G^-2
⇒ [ML²T^-2][ML²T^-1]²[M]^-5[M^-1L³T^-2]^-2
= ML³T^-2 × M²L⁴T^-2 × M^-5 × M²L^-6T⁴ = M^1+2-5+2L^2+4-6T^-2-2+4 = M⁰L⁰T⁰
కాబట్టి P=El²m^-5G^-2 కు మితులు లేవు.

ప్రశ్న 2.
కాంతి వేగము c, ప్లాంక్ స్థిరాంకము h మరియు విశ్వగురుత్వ స్థిరాంకము G లను ప్రాథమిక భౌతిక రాశులుగా తీసుకొని ద్రవ్యరాశి, పొడవు, కాలములకు మితిఫార్ములాలు వ్రాయండి.
సాధన:
కాంతి వేగము cకి మితి ఫార్ముల = LT^-1;
ప్లాంక్ స్థిరాంకం h కి మితిఫార్ముల= ML²T^-1
విశ్వ గురుస్థిరాంకం Gకి మితిఫార్ముల = M^-1L³T^-2
ద్రవ్యరాశి [M] = c^xh^yG^z ⇒ M¹L⁰T⁰ = [LT^-1]^x[ML²T^-1]^y[M^-1L³T^-2]^z
⇒ M¹L⁰T⁰ = L^xT^-x × M^yL^2yT^-y × M^-zL^3zT^-2z
⇒ M¹L⁰T⁰ = M^y-zL^x+2y+3zT^-x-y-2z
ఘాతాంకములను పోల్చగా y – z = 1 …..(1); x + 2y + 3z = 0 …..(2); -x – y – 2z = 0 ……(3)

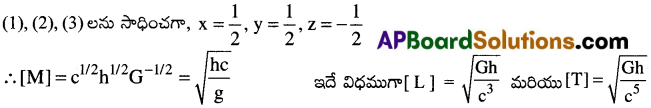
ప్రశ్న 3.
M ద్రవ్యరాశి, R వ్యాసార్థము గల ఒక గ్రహము చుట్టూ r వ్యాసార్థము గల కక్ష్యలో ఒక కృత్రిమ ఉపగ్రహము పరిభ్రమించుచున్నది. దాని పరిభ్రమణ కాలమునకు సమీకరణము T = \(\frac{k}{R}\sqrt{\frac{r^3}{g}}\) అని చూపుము. kఒక మితులు లేని స్థిరాంకము మరియు g గురుత్వ త్వరణం.
సాధన:
M ద్రవ్యరాశి, R వ్యాసార్ధము గల ఒక గ్రహము చుట్టూ r వ్యాసార్థము గల కక్ష్యపై ఆధారపడినట్లయితే ఆ కృత్రిమ ఉపగ్రహము యొక్క పరిభ్రమణ కాలము (T) T = kr^aG^bM^c
k అనునది మితిరహిత స్థిరాంకం. ఇరువైపులా మితి ఫార్ములాలను తీసుకున్నయిట్లతే
[M⁰L⁰T¹] = [L]^a [M^-1L³T^-2]^b [M]^c ⇒ [M⁰L⁰T¹] = [L]^a [M^-bL^3bT^-2b] [M]^c
⇒ [M⁰L⁰T¹] = [M^-b+cL^a+3bT^-2b] ఇరువైపులా M, L, T మితులను పోల్చగా,

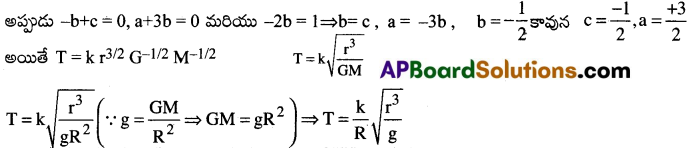
ప్రశ్న 4.
ఈ క్రింది వానిలో ఎన్ని సార్థక అంకెలు ఉన్నవి?
(a) 6729 (b) 0.024 (c) 0.08240 (d)6.032 (e) 4.57 × 10⁸.
సాధన:
(a) 6729 : దీనిలోని సార్థక అంకెల సంఖ్య 4
కారణం : సున్న కాని అంకెలు సార్థక అంకెలు.

(b) 0.024 : దీనిలోని సార్థక అంకెల సంఖ్య 2. అవి 2,4
కారణం: ఇచ్చిన సంఖ్య 1 కంటే తక్కువయినప్పుడు దశాంశ బిందువునకు కుడివైపున మొదటి సున్నకాని అంకెకు మధ్యలో ఉన్న సున్నాలు సార్థక అంకెలు కావు.

(c) 0.08240: దీనిలోని సార్థక అంకెలు 4 అవి 8,2,4,0
కారణం: దశాంశ స్థానము ఉన్నపుడు చివరలో ఉన్న సున్నాలు సార్థక అంకెలు అవుతాయి.

(d) 6.032: దీనిలోని సార్థక అంకెల సంఖ్య 4. అవి 6, 0, 3, 2
కారణం : దశాంశ బిందువు ఎక్కడ ఉన్న, రెండు సున్న కాని అంకెల మధ్య గల సున్నాలు సార్థక అంకెలు అవుతాయి

(e) 4.57 × 10⁸: ఇందులోని సార్థక అంకెల సంఖ్య 3. అవి 4,5,7
కారణం: సార్థక అంకెలను నిర్ణయించునపుడు 10 యొక్క ఘాతము (ఇక్కడ 8) లెక్కలోనికి రాదు.

ప్రశ్న 5.
ఒక కర్ర ముక్క పొడవు 12.132 సెం.మీ. ఇంకొక దాని పొడవు 12.4 సెం.మీ . ఒక కర్ర ముక్క చివర రెండవ దానిని ఉంచిన మొత్తము పొడవు ఎంత? ఆ రెండు కర్ర ముక్కలను ప్రక్క ప్రక్కన ఉంచిన, వాని పొడవుల లోని తేడా ఎంత?
సాధన:
l₁ = 12.132 సెం.మీ మరియు l₂ = 12.4 సెం.మీ
కర్ర ముక్కలను ఒక దాని చివర రెండవది ఉంచినపుడు మొత్తము పొడవు = l₁ + l₂ = 12.132 + 12.4 = 24.532 సెం.మీ = 24.5 సెం.మీ

కర్ర ముక్కలను ప్రక్క ప్రక్కన ఉంచినపుడు వాని పొడవులలోని తేడా l₂ – l₁ = 12.4 – 12.132 – 0.268 = 0.3 సెం.మీ

కారణం:
l₁, l₂ లలో l₂ లో దశాంశ బిందువు తరువాత ఒక స్థానము, l₁ లో మూడు స్థానములు ఉన్నవి.
జవాబులో, తీసుకున్న సంఖ్యలలో తక్కువ దశాంశ స్థానములు ఎన్ని ఉన్నవో, అన్ని ఉంచవలయును.

ప్రశ్న 6.
ఒక ఘనము యొక్క భుజము 7.203 మీ. అయిన (i) దాని మొత్తము ఉపరితలము వైశాల్యము (ii) ఘనపరిమాణంను కనుక్కోండి సార్థక అంకెల ప్రకారం జవాబు నివ్వండి.
సాధన:
ఘనము యొక్క భుజము, s = 7.203 మీ
ఘనము యొక్క మొత్తము ఉపరితల వైశాల్యం, A = 6s² = 6(7.203)² = 6 × 51.883209
= 311.299254 m² = 311.3 m²

ఘనము యొక్క ఘనపరిమాణం V = s³ = (7.203)³ = 373.7147544 మీ³ = 373.7 మీ³ = 373.7 మీ³.
కారణం:
ఘనము యొక్క భుజము కొలతలో నాలుగు సార్థక అంకెలు ఉన్నవి. కావున జవాబులో కూడ నాలుగు సార్థక అంకెలు మాత్రమే ఉండవలయును.

ప్రశ్న 7.
ఒక వస్తువునకు కొలిచిన ద్రవ్యరాశి, ఘనపరిమాణములు వరుసగా 2.42 గ్రా. మరియు 4.7 సెం.మీ³ ద్రవ్యరాశి, ఘనపరిమాణములలోని దోషములు 0.01గ్రా, 0.1 సెం.మీ³. అయిన సాంద్రత కొలతలోని గరిష్ట దోషము ఎంత?
సాధన:
కొలిచిన ద్రవ్యరాశి, m = 2.42 గ్రా.
కొలిచిన ఘనపరిమాణం, v = 4.7 సెం.మీ³
ద్రవ్యరాశిలోని దోషం, ∆m = 0.01 గ్రా.
ఘనపరిమాణం లోని దోషం, ∆V = 0.1 సెం.మీ³

కారణం:
భాగహారము, హెచ్చువేతలలో తీసుకున్న సంఖ్యలలో, ఏ సంఖ్యలో కనిష్ట సార్థక సంఖ్యలు ఉన్నవో, జవాబులో అన్ని సార్థక అంకెలు మాత్రమే ఉంచవలయును.
ద్రవ్యరాశిలో 3, ఘనపరిమాణంలో రెండు సార్థక అంకెలు ఉన్నవి. ఘనపరిమాణంలో తక్కువ సార్థక అంకెలు ఉన్నవి. అవి 2. అందువలన జవాబులో కూడ 2 సార్థక అంకెలు మాత్రమే ఉండవలయును.

ప్రశ్న 8.
ఒక గోళము వ్యాసార్థము కొలతలో వచ్చిన దోషం 1% అయిన దాని ఘనపరిమాణం కొలతలో వచ్చు దోష శాతం ఎంత?
సాధన:

∴ కావున గోళము ఘనపరిమాణం కొలతలోని దోష శాతం 3%

ప్రశ్న 9.
ద్రవ్యరాశి, వేగము కొలతలోని దోష శాతములు వరుసగా 2%, 3% అయిన గతిశక్తి కొలతలోని గరిష్ట దోష శాతం ఎంత? [AP 18, 20][TS 20]
సాధన:

∴ గతి శక్తిలోని దోషశాతం = 8%

ప్రశ్న 10.
సాధారణ పీడనము, ఉష్ణోగ్రత వద్ద ఒక మోల్ వాయువు ఆక్రమించు ఘనపరిమాణం 22.4 లీటర్లు (దీనిని మోలార్ ఘనపరిమాణం అని అంటారు). హైడ్రోజన్ అణువు సైజు సుమారుగా 1Å అయిన హైడ్రోజన్ మోలార్ ఘనపరిమాణంకు హైడ్రోజన్ అణువుల ఘనపరిమాణమునకు నిష్పత్తి ఎంత?
సాధన:
హైడ్రోజన్ అణువు వ్యాసము = 1Å = 1 × 10^-10 మీ

ప్రశ్న 11.
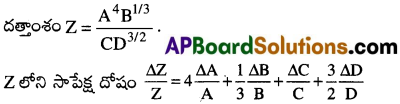
Z = \(\frac{A^4 B^{1 / 3}}{C D^{3 / 2}}\) అయిన Z లోని సాపేక్షదోషాన్ని కనుగొనుము. [TS MAY 19]
సాధన: