AP Inter 1st Year Physics Important Questions Chapter 11 ప్రవాహుల యాంత్రిక ధర్మాలు

Students get through AP Inter 1st Year Physics Important Questions 11th Lesson ప్రవాహుల యాంత్రిక ధర్మాలు which are most likely to be asked in the exam.

AP Inter 1st Year Physics Important Questions 11th Lesson ప్రవాహుల యాంత్రిక ధర్మాలు

Very Short Answer Questions (అతిస్వల్ప సమాధాన ప్రశ్నలు)

ప్రశ్న 1.
సగటు పీడనమును నిర్వచించి, దాని ప్రమాణములను, మితి ఫార్ములాను వ్రాయండి. అది అదిశరాశా లేక సదిశరాశా? [AP 17,20]
జవాబు:
ఏకాంక వైశాల్యము పై పని చేయు అభిలంబ బలమును సగటు పీడనము అని అంటారు.

వైశాల్యము పై పని చేయుచున్న అభిలంబ బలము F అయితే ఆ వైశాల్యము పై సగటు పీడనం P_ave = \(\frac{F}{A}\)
S.I ప్రమాణం నూ.మీ^-2 (లేక ) పాస్కల్
మితి ఫార్ములా: [ML^-1T^-2]
సగటు పీడనం అదిశరాశి

ప్రశ్న 2.
స్నిగ్ధతను నిర్వచించి, ప్రమాణములు మరియు మితి ఫార్ములా వ్రాయండి? [Imp.Q][May 13][TS 15, 18][AP 16]
జవాబు:
స్నిగ్ధత :
ఒక ప్రవాహిలోని విభిన్న పొరల మధ్య గల సాపేక్ష చలనము ను నిరోధించు ప్రవాహి ధర్మమును స్నిగ్ధతలని అంటారు.
S.I ప్రమాణము స్వాజూలీ (లేక) pa s
మితి ఫార్ములా: [ML^-1T^-1]

ప్రశ్న 3.
ఒక మోటారు వాహనములోని కార్బ్యురేటర్ పనిచేయు సూత్రము ఏమిటి? [TS 17,18][AP 15,19,19]
జవాబు:
మోటారు వాహనములోని కార్బురేటర్ బెర్నూలీ సిద్ధాంతము ఆధారముగా పనిచేయును.

పనిచేయు విధానము :
కార్బురేటర్ నందు సన్నని ముఖ ద్వారము గల ఒక వెంటూరి గొట్టము ఉండును. దీని ద్వారా గాలి చాలా ఎక్కువ వేగముతో ప్రవహించును. అపుడు సన్నని ద్వారము వద్ద పీడనము బాగుగా తగ్గును. దీని వలన దహనము చెందుటకు కావలసిన పాళ్ళలో గాలి, పెట్రోలు వచ్చునట్లుగా పెట్రోలు పైకి పీల్చబడును.

ప్రశ్న 4.
మాగ్నస్ ప్రభావం అనగా ఏమి? [Imp.Q][AP 15,17,18][TS 19,22]
జవాబు:
ఆత్మ భ్రమణం చేయుచూ (ముందుకు) ప్రయాణిస్తున్న బంతి పై భాగమున గాలి వేగము ఎక్కువ గాను, క్రింది భాగమున గాలి వేగము తక్కువగాను ఉండును. దీని వలన బంతి పై భాగమున తక్కువ పీడనం, క్రింది భాగమున ఎక్కువ పీడనం కలుగును.పీడనాల తేడా వలన భ్రమణంతో విసిరి వేయ బడ్డ బంతి పై నికరమైన ఊర్ధ్వాభి బలం పని చేస్తుంది. ఈ కారణం చేత బంతి పథం వక్రంగా ఉంటుంది. ఈ ప్రభావాన్ని మాగ్నస్ ఫలితం అని అంటారు.

ప్రశ్న 5.
ద్రవ బిందువులు మరియు బుడగలు గోళాకారంగా ఎందుకు ఉంటాయి? [AP 22][AP,TS 16,17,18]
జవాబు:
ద్రవం ఉపరితలము ఎల్లప్పుడు కనిష్ట వైశాల్యమును పొందుటకు ప్రయత్నించును. నియమిత ఘనపరిమాణంకు అన్ని ఆకారముల లోను గోళాకారమునకు కనిష్ట వైశాల్యము ఉండును. అందువలన ద్రవ బిందువులు మరియు బుడగలు గోళాకారంగా ఉండును.

ప్రశ్న 6.
ఒక ద్రవ బిందువులోని అధిక పీడనమునకు సమీకరణమును వ్రాయండి. [AP 19] [TS 17, 20]
జవాబు:
ద్రవ బిందువు లోపలి అధిక పీడనము = P_inside – P_outside ⇒ P_excess = \(\frac{2T}{r}\)
ఇక్కడ r = ద్రవ బిందువు వ్యాసార్థము, T = ద్రవము యొక్క తలతన్యత

ప్రశ్న 7.
ఒక ద్రవములోని గాలి బుడుగ లోపలి అధిక పీడనమునకు సమీకరణమును వ్రాయుము. [Imp.Q]
జవాబు:
ఒక ద్రవములోని గాలి బుడుగకు ఒక స్వేచ్ఛా ఉపరితలము మాత్రమే ఉండును. అందువలన గాలి బుడుగ
లోపలి అధిక పీడనం P = \(\frac{2T}{r}\)

ప్రశ్న 8.
గాలిలో ఉన్న సబ్బు బుడగ లోపలి అధిక పీడనమునకు సమీకరణమును వ్రాయండి. [AP 19][TS 22]
జవాబు:
గాలిలో ఉన్న సబ్బు బుడగకు రెండు స్వేచ్ఛా ఉపరితలములు ఉండును. అందువలన సబ్బు బుడగలో అధిక
పీడనం = P_inside – P_outside ⇒ P_excess = \(\frac{4T}{r}\)
ఇక్కడ r = సబ్బు బుడగ వ్యాసార్థము, T = సబ్బు నీటి తలతన్యత

ప్రశ్న 9.
జల సంసక్తకాలు మరియు జల అసక్తకాలు అనగా ఏమి? అవి ఏమి చేయును? [Imp.Q]
జవాబు:
నీరు చొచ్చుకొని పోవుటకు వీలు కాని పదార్థము లేక గుడ్డను జల అసక్తకాలు అని అంటారు. ఇవి నీటికి, పదార్థమునకు లేక గుడ్డకు మధ్య గల స్పర్శ కోణమును పెంచును.

సబ్బులు,డిటర్జెంట్లు మరియు వస్త్రములకు రంగు అద్దు పదార్థములు జల సంసక్తకాలకు ఉదాహరణ.

ఇవి స్పర్శకోణమును మరియు నీటి తలతన్యతను తగ్గించుట ద్వారా నీరు వస్తువులలోనికి చొచ్చుకొని పోవునట్లు చేయును.

ప్రశ్న 10.
గాజు ఉపరితలమును నీటి బిందువులు తడుపును కాని తామరాకుని నీటి బిందువులు తడపవు ఎందువలన? [AP 20][TS 15]
జవాబు:
గాజు ఉపరితలమునకు స్పర్శకోణం 90°ల కంటే తక్కువ. కావున నీటి బిందువులు గాజు ఉపరితలమును తడుపును. తామరాకు యొక్క స్పర్శకోణం 90°ల కంటే ఎక్కువ. కావున నీటి బిందువులు తామరాకును తడపవు.

ప్రశ్న 11.
స్పర్శ కోణము అనగా ఏమి? [Imp.Q][AP 16][TS 20]
జవాబు:
స్పర్శ కోణం :
ఘన తలానికి, ఘన తలం ద్రవం కలిసే బిందువు వద్ద ద్రవ అంతర్భాగంలో ద్రవతలాన్ని స్పృశిస్తూ గీసిన స్పర్శరేఖకు మధ్యగల కోణాన్ని ఆ ఘనద్రవాల జంటకు సంబంధించిన స్పర్శకోణం అని అంటారు.

ప్రశ్న 12.
బెర్నౌలీ సిద్ధాంతమునకు రెండు ఉదాహరణలిచ్చి, వివరించండి. [AP 18][Imp.Q][TS 15]
జవాబు:
i) గతిక ఉత్థాపన :
ఒక ప్రవాహిలో గమనంలో ఉన్న వస్తువుపై పనిచేసే ఊర్ధ్వ బలాన్నే గతిక ఉత్థాపన అంటారు.

ii) విమానం రెక్కలపై గతిక ఉత్థాపనం :
విమానం రెక్క మధ్యచ్ఛేద ఆకారంలో రెక్క క్రింది వైపు పుటాకార ఆకారాన్ని కలిగి ఉంటుంది.

బెర్నౌలీ సమీకరణం ప్రకారం పై తలం మీద తక్కువ పీడనం, దిగువ తలం మీద ఎక్కువ పీడనం ఉండడం వల్ల ఏర్పడిన పీడన వ్యత్యాసం విమానానికి కావలసిన ఉత్థాపనాన్ని కలిగిస్తుంది.

iii) భ్రమణంలో ఉన్న బంతిపై గతిక ఉత్థాపన :
ఒక బంతి గాలిలో కొంత వేగంతో (v) ప్రయాణిస్తుంటే, ఆత్మభ్రమణం వలన దాని చుట్టూ ధారారేఖలు ఏర్పడతాయి.

బెర్నౌలీ సిద్ధాంతం ప్రకారం, ప్రవాహి యొక్క వేగం పెరిగితే, అక్కడ పీడనం తగ్గుతుంది. వేగం తగ్గితే పీడనం పెరుగుతుంది. ఈ వేగాల తేడా వల్ల బంతిపై పనిచేసే ఫలిత ఊర్ధ్వబలాన్ని గతిక ఉత్థాపనం అంటారు.

ప్రశ్న 13.
ఒక గొట్టము గుండా నీరు ప్రవహిస్తున్నపుడు ఏ పొర వేగముగాను మరియు నిదానముగాను కదులును ?[Imp.Q] [TS 15]
జవాబు:
గొట్టము యొక్క గోడలను ఆనుకుని ఉండే పొరలు నిదానముగా కదులును. మరియు కేంద్రభాగములో ఉండే పొరలు వేగముగా కదులును.

ప్రశ్న 14.
ఒక వస్తువు ఉపరితల వైశాల్యం పెరిగితే దాని చరమవేగం పెరుగుతుంది. ఒప్పా లేక తప్పా? వివరించండి. [Imp.Q]
జవాబు:
సత్యము. చరమవేగం V_t α r² ⇒ V_t α 4πr² ⇒ V_t α A, [A = 4πr² = గోళం ఉపరితల వైశాల్యం]

Short Answer Questions (స్వల్ప సమాధాన ప్రశ్నలు)

ప్రశ్న 1.
వాతావరణ పీడనం అంటే ఏమిటి? భారమితి సహాయంతో దీన్ని ఎలా నిర్ధారిస్తారు? [Imp.Q]
జవాబు:
వాతావరణ పీడనం :
ఏదైనా ఒక బిందవు వద్ద వాతావరణ పీడనం, ఆ బిందువు నుంచి విస్తరిస్తూ వాతావరణపు పై అంచుదాకా కొనసాగే ఏకాంక మధ్యచ్ఛేద వైశాల్యం గల వాయుస్తంభం యొక్క బరువుకు సమానం.

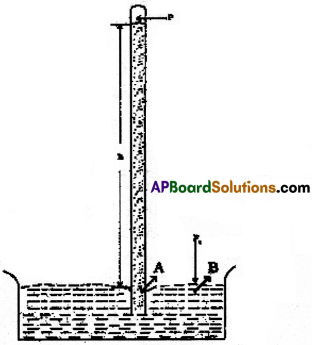
భారమితి :
ఒక కొనవైపు మూసి ఉన్నటువంటి ఒక గాజు గొట్టంలో పాదరసాన్ని నింపి, దానిని ఒక పాదరసం తొట్టెలో పటంలో చూపిన విధంగా బొర్లిస్తారు. ఈ పరికరాన్నే పాదరస భారమితి అని అంటారు. గొట్టంలో నిలిచిన పాదరస స్తంభం ఎగువన ఉన్న ప్రదేశంలో ఉండేదల్లా పాదరస భాష్పం మాత్రమే. దీని పీడనమును నిర్లక్ష్యము చేయవచ్చు. స్తంభం లోపల ఒక బిందువు A వద్ద ఉన్న పీడనం అదే మట్టం వద్ద ఉన్న బిందువు B వద్ద ఉండే పీడనంతో సమానం. B వద్ద పీడనం వాతావరణ పీడనము P_a కు
సమానం. P_a = hρg
ఇక్కడ ρ = పాదరసం సాంద్రత
h = గాజు గొట్టములో పాదరస స్తంభం ఎత్తు
p_a = వాతావరణ పీడనం
g = గురుత్వ త్వరణం

ప్రశ్న 2.
గేజ్ పీడనం అంటే ఏమిటి? మానోమీటర్ సహాయంతో పీడన వ్యత్యాసాన్ని ఎలా కనుక్కొంటారు? [Imp.Q]
జవాబు:
ఒక వ్యవస్థ పీడనము (P) నకు, వాతావరణ పీడనము (P_a) నకు మధ్యగల తేడా (P – P_a) ను గేజ్ పీడనం అని అంటారు.

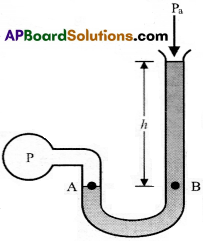
మానోమీటర్ :
పీడన వ్యత్యాసాలను కొలవడానికి ఉపయుక్తమైన ఒక పరికరం తెరచిన గొట్టం ఉన్న మానోమీటర్. ఇందులో ఒక అనువైన ద్రవంతో నింపిన U గొట్టం ఉంటుంది. ఈ U గొట్టంలో ఒక కొన వాతావరణంతో సంబంధం ఉండేటట్లుగా తెరచి ఉన్నది కాగా, మరో కొన, మనం ఏ వ్యవస్థ పీడనాన్నైతే కొలవదలుచుకొన్నామో, ఆ వ్యవస్థకు కలపబడి ఉంటుంది.
A వద్ద పీడనం = B వద్ద పీడనం
P = P_a + hρg ⇒ P – P_a = గేజ్ పీడనం P_g = hρg

మానోమీటర్ లోని రెండు పాదరస స్తంభముల ఎత్తులలోని తేడా (h) కు గేజ్ పీడనం అనులోమాను పాతంలో ఉంటుంది.

ప్రశ్న 3.
పాస్కల్ నియమాన్ని తెలిపి ఒక ప్రయోగం సహాయంతో దాన్ని నిరూపించండి. [Imp.Q]
జవాబు:
పాస్కల్ నియమం :
విరామ స్థితిలో ఉన్న ఒక ప్రవాహిలో ఒకే ఎత్తులో ఉన్న అన్ని బిందువుల వద్ద, పీడనం ఒకే విలువ కలిగి ఉంటుంది. దీనిని పాస్కల్ నియమం అని అంటారు.

ప్రయోగం :
విరామ స్థితిలో ఉన్న ఒక ప్రవాహి లోపల ABC – DEF అను ఒక స్వల్పాంశ లంబకోణ పట్టకాకృతిని ఊహించుము. దాని ప్రతిభాగం ద్రువ ఉపరితలం నుండి ఒకే లోతులో ఉండును. కావున అన్ని బిందువులపై గురుత్వ ప్రభావం సమానం. BEFC, ADFC మరియు ADEB ముఖాల వైశాల్యంశములు వరుసగా A_a, A_b మరియు A_c. వీని పై పని చేయుచున్న అభిలంబ బలాలు F_a, F_b మరియు F_c. వీని వల్ల ప్రవాహి కలుగ జేయుచున్న పీడనములు P_a, P_b మరియు P_c.
అపుడు F_bsinθ₂ = F_c, F_bcosθ₂ = F_a (సమతాస్థితి వల్ల)

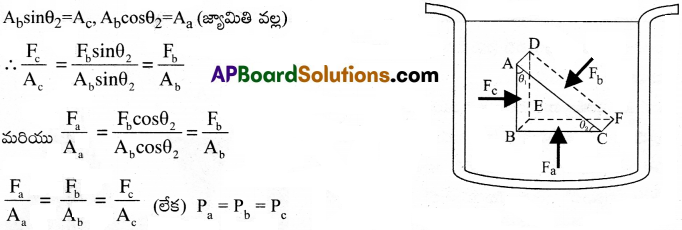
కనుక నిశ్చల స్థితిలో ఉన్న ద్రవములో సమాన లోతు వద్ద గల బిందువుల వద్ద సమానమైన పీడనములు ఉండును. (లేక) నిశ్చల స్థితిలో ఉన్న ద్రవములోని ఏదేని ఒక బిందువు వద్ద కలుగజేసిన పీడనము ద్రవములోని అన్ని బిందువుల వద్దకు అదే విధముగా వ్యాప్తి చెందును.

ప్రశ్న 4.
హైడ్రాలిక్ లిఫ్ట్ (ద్రవ ఆధారిత లిఫ్ట్) మరియు హైడ్రాలిక్ బ్రేక్ (ద్రవ ఆధారిత బ్రేకు) లను వివరించండి.
జవాబు:

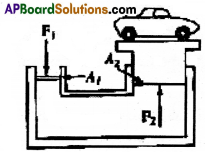
హైడ్రాలిక్ లిఫ్ట్ లోని రెండు ముషలకాలు వాటి మధ్య నింపిన ద్రవంతో వేరయి ఉంటాయి. అల్పమధ్యచ్ఛేద వైశాల్యం A₁ కలిగిన ముషలకాన్ని ద్రవం పై నేరుగా F₁ అనే బలాన్ని ప్రయోగించడానికి వాడతారు. పాస్కల్ నియమం ప్రకారం, దీని వలన కలిగిన పీడనం P₁ = \(\frac{F_1}{A_1}\) ఎక్కువ మధ్యచ్ఛేద వైశాల్యం A₂ గల మరొక ముషలకానికి అందుతుంది. ఇది PA₂ అనే ఉర్థ్వబలం ఉత్పన్నమగుటకు కారణమవుతుంది. అందువల్ల ఆ ముషలకం పెద్ద పెద్ద భారాలను మోయగలుగుతుంది.

కావున చిన్న ముషలకము పై ప్రయోగించిన F₁ అనే స్వల్ప బలం, పెద్ద ముషలకము పై F₂ అనే అధిక బలమును కలుగజేయును. ఇదే హైడ్రాలిక్ యంత్రం యొక్క సూత్రం.

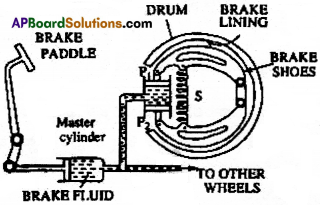
హైడ్రాలిక్ బ్రేకులు :
మన పాదంతో పెడల్ పైన మనం ఒక స్వల్ప బలాన్ని ప్రయోగిస్తే, మాస్టర్ స్థూపంలోని మాష్టర్ ముషలకం కదులుతుంది. ఇందువల్ల కలిగే పీడనం బ్రేక్ నూనె ద్వారా ప్రసరితమై దీని కంటే ఎక్కువ వైశాల్యం గల ముషలకం పైన చర్య జరుపుతుంది. ఇందువల్ల ఒక అత్యధిక బలం ఆ ముషలకంపై చర్య జరిపి, అది కిందకు నెట్టబడుతుంది. తద్వారా బ్రేక్ లైనింగ్కు వ్యతిరేకంగా బ్రేక్షూలు వ్యాకోచం చెంది, అంటే అవి ముందుకు జరిగి, బ్రేక్ లైనింగ్ను గట్టిగా ఒడిసిపట్టుకుంటాయి.

ప్రశ్న 5.
ద్రవ స్థితిక విరోధ భాసం అనగా ఏమి? [TS 19]
జవాబు:
హైడ్రాస్టిక్ పారడాక్స్ :
పాత్ర ఆకారము, ఆధార వైశాల్యము పై ఆధారపడకుండ, ఒకే క్షితిజ సమాంతర తలములో ఉండు అన్ని బిందువుల వద్ద ద్రవ పీడనము సమానముగా ఉండును.

ఉదాహరణ:
పటములో చూపినట్లు వేర్వేరు ఆకారము గల A, B, C అను మూడు పాత్రలను తీసుకొని వాని అడుగు భాగములను ఒక క్షితిజ సమాంతర గొట్టముతో కలపండి. ఇపుడు నీటితో నింపిన, వేర్వేరు పాత్రలలో వేర్వేరు మొత్తములలో నీరు ఉన్నప్పటికి, అన్నిటిలోను నీటిమట్టము ఒకే ఎత్తులో ఉండును. ప్రతి పాత్ర అడుగున క్షితిజ సమాంతర గొట్టములో ఒకే పీడనము ఉండుట దీనికి కారణము.

ప్రశ్న 6.
లోతుతో పీడనము ఎలా మారుతుందో వివరించండి.
జవాబు:
ఒక పాత్రలో నిశ్చల స్థితిలో ఉన్న ద్రవమును ఊహించుము. పటములో చూపినట్లు ఆధార వైశాల్యము A ఎత్తు h గల ఒక స్థూపాకార ద్రవ మూలకమును ఊహించుము. 1 మరియు 2 బిందువుల వద్ద పీడనములు వరుసగా p₁, p₂ అని అనుకొనుము. స్థూపాకార ద్రవ మూలకము యొక్క వక్రతా ఉపరితలము పై పనిచేయు క్షితిజ సమాంతర బలములు పరస్పరము సంతులనము చేసుకొనును. ద్రవ మూలకము పై పనిచేయుచున్న నిలువు తలములోని బలములు మూడు. అవి

i) ద్రవ మూలకము పై భాగమున నిట్టనిలువుగా క్రింది దిశలో పనిచేయు బలము P₁A
ii) ద్రవ మూలకము అడుగు భాగము పై నిట్టనిలువుగా పై దిశలో పనిచేయు బలము P₂A
iii) స్థూపాకార ద్రవమూలకము యొక్క భారము mg ఇది నిట్ట నిలువుగా క్రింది దిశలో ద్రవమూలకము యొక్క గరిమనాభి స్థానము నుండి పని చేయు చుండును. ద్రవమూలకము సమతా స్థితిలో ఉన్నది కనుక

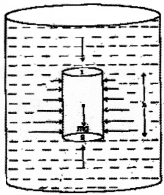
∴ ∑F_Y = 0
P₁A + mg – P₂A = 0 (or) (P₂ – P₁)A = mg
ద్రవము యొక్క సాంద్రత ρ అయితే ద్రవ మూలకము లోని ద్రవము ద్రవ్యరాశి m = hA ρ
∴ (P₂ – P₁)A = hA ρ g (లేక) P₂ – P₁ = hρ g. …….. (1)
బిందువు 1 ను ద్రవ ఉపరితలము వద్ద ఊహించిన P₁ = P_a, వాతావరణ పీడనమునకు సమానమగును. అదే విధముగా p₂ = p అనుకొనుము. ఇపుడు (1) వ సమీకరణమును ఈ క్రింది విధముగా వ్రాయవచ్చును.
P – P_a = hρg (లేక) P = P_a + hρg ………….. (2)

అనగా ద్రవ ఉపరితలము నుండి లోతుకు వెళ్ళుచున్న కొలది పీడనము పెరుగుచుండును.

ప్రశ్న 7.
టోరిచెల్లి సిద్ధాంతము ఏమిటి? ఒక ప్రయోగంతో బహిస్రావ వడిని ఎలా నిర్ధారిస్తారో వివరించండి.
జవాబు:
టోరిచెల్లి సిద్ధాంతం :
ఒక సన్న రంధ్రం ద్వారా బహిర్గతమయ్యే ద్రవపు బహిస్రావ వేగము, ఆ ద్రవపు ఉపరితలం నుండి రంధ్రము వరకు స్వేచ్ఛగా ద్రవం నిట్టనిలువుగా పడునపుడు ద్రవం (లేదా వస్తువు) పొందే తుది వేగానికి సమానం.

ద్రవం ఉపరితలం వద్ద పీడనం P₁,వేగం v₁, ద్రవం ఎత్తు h₁ అనుకొనుము. రంధ్రం వద్ద వీని అనురూప విలువలు P₂, v₂ మరియు h₂ అనుకొనుము. ద్రవసాంద్రత ‘ρ’ అనుకొనుము.

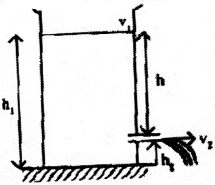
బెర్నౌలి సమీకరణం ప్రకారం

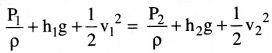
కాని P₁ = P₂ = వాతావరణ పీడనం ఎందువలన అనగా రంధ్రము, ద్రవ ఉపరితలము వాతావరణ పీడనమునకు తెరచి ఉన్నవి. రంధ్రం వైశాల్యం A₂ తో పోల్చిన ద్రవ ఉపరితల వైశాల్యం A₁ చాలా ఎక్కువ. కనుక v₁ << v₂, కనుక v₁² ను నిర్లక్ష్యం చేయవచ్చు.

ప్రశ్న 8.
వెంటూరి మీటర్ అనగా ఏమి? దీన్ని ఎలా ఉపయోగిస్తారో వివరించండి. [Imp.Q]
జవాబు:
ఇంజనీర్ G.B. వెంటూరీ ఈ సాధనాన్ని నిర్మించాడు. కావున దీనిని వెంటూరీ మీటర్ అని అంటారు. ద్రవ వేగంతో పీడనం మారే విధానం ఆధారంగా వెంటూరీ మీటర్ పని చేస్తుంది. ఈ సాధనాన్ని క్షితిజ సమాంతరంగా ఉన్న గొట్టంలోని ద్రవ ప్రవాహ వేగాన్ని (లేదా ప్రవాహపు రేటు కనుక్కోవడానికి ఉపయోగిస్తారు.

పటములో చూపిన విధంగా ఒక విశాలమైన వ్యాసంతో, మధ్యలో ఒక చిన్న నొక్కును కలిగి ఉన్న ఒక గొట్టం ఉంటుంది. U ఆకారంలో ఉన్న ఒక మానోమీటర్ దీనికి అనుసంధానించి ఉంటుంది. మానోమీటర్ లోని ద్రవసాంద్రత ρ_m అనుకొనుము. వెడల్పైన కుత్తుక వద్ద మధ్యచ్ఛేద వైశాల్యము A, ద్రవ పీడనం P₁ ద్రవ వేగము V₁ అనుకొనుము. సన్నని కుత్తుక వద్ద మధ్యచ్ఛేద వైశాల్యం a ద్రవ పీడనంP₂, ద్రవ వేగం V₂ అనుకొనుము. సాంతత్య సమీకరణం ప్రకారం

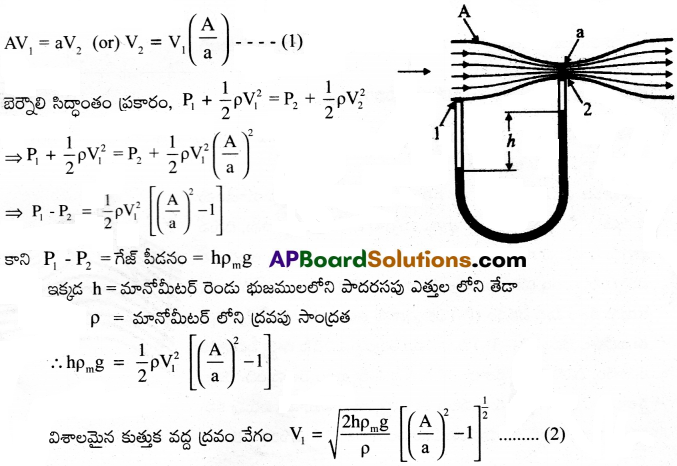
ప్రశ్న 9.
రేనాల్డ్స్ సంఖ్య అనగా ఏమి? దాని ప్రాముఖ్యత ఏమిటి? [Imp.Q]
జవాబు:
ఒక గొట్టములో ప్రవహించు ద్రవపు లక్షణము లేక రకమును నిర్ణయించు మితిరహిత సంఖ్యను రేనాల్డు సంఖ్య అని అంటారు.
R_C = \(\frac{\rho v d}{\eta}\)
ఇక్కడ ρ = ద్రవ సాంద్రత
v = ద్రవ వేగము
d = గొట్టము యొక్క వ్యాసము
η = ద్రవము యొక్క స్నిగ్ధతా గుణకం

ప్రాముఖ్యత:

1. జడత్వ బలమునకు, చలనములో ఉన్న ద్రవపు స్నిగ్ధతా బలమునకు మధ్య నిష్పత్తిని రేనాల్డు సంఖ్య సూచించును.
2. R_Cకు సమానమగు సందిగ్ధ వేగముల వద్ద జ్యామితీయంగా ఒకే పోలిక గల ప్రవాహములు సంక్షుబ్ద ప్రవాహములు అగునని నిరూపితమయినది. ఇందువలన పెద్ద పెద్ద ఓడలు, సబ్మెరైన్లు, విమానములు, పోటీలలో పాల్గొను కార్ల నిర్మాణము, మరియు ప్రయోగశాలలో ద్రవ ప్రవాహ లక్షణములను తెలుసుకొనుటకు చిన్న చిన్న నమూనాలు తయారుచేయుట సాధ్యమగును.
3. స్తరీయ గతికి రేనాల్డు సంఖ్య 1000 కంటే తక్కువగా ఉండును.
4. రేనాల్డు సంఖ్య 2000 దాటినచో అది సంక్షుబ్ద ప్రవాహనము.
5. రేనాల్డు సంఖ్య 1000కి 2000కి మధ్య ఉన్నచో ప్రవాహము స్తరీయగతి సంక్షుబ్ద ప్రవాహముల మధ్య మారుచుండును.అనగా అది నిలకడ రహిత ప్రవాహంగా మారుతుంది.

ప్రశ్న 10.
గతిక ఉత్థాపనాన్ని ఉదాహరణలతో సహా వివరించండి. [Imp.Q]
జవాబు:
గతిక ఉత్థాపన :
ఒక ప్రవాహిలో ఒక వస్తువు చలనంలో ఉన్నపుడు ఆ వస్తువు పై ఊర్ధ్వ బలము పనిచేయును. దీనినే గతిక ఉత్థాపన అని అంటారు.

ఉదాహరణ : విమానం రెక్కల పై గతిక ఉత్థాపన :
విమానం ప్రయాణించు చున్నపుడు, విమానపు రెక్కల పై భాగమున గాలి వేగము ఎక్కువగాను, దిగువ భాగమున తక్కువ గాను ఉండునట్లు రెక్కల నిర్మాణం ఉండును. అందుచేత బెర్నౌలి సిద్ధాంతం ప్రకారం రెక్కల పై భాగాన (P₁) పీడనం తక్కువ గాను, అడుగు తలం మీద పీడనం (P₂) ఎక్కువగాను ఉంటుంది. అంటే(P₂ > P₁). ఈ పీడనాల భేదం (P₂ – P₁) విమానము రెక్కలపై పనిచేసే ఊర్థ్వ పీడనానికి సమానం. దీనిని రెక్కల వైశాల్యంతో గుణిస్తే ఊర్థ్వ బలం తెలుస్తుంది. రెక్కల వైశాల్యం ఎక్కువగా ఉండుట వలన ఈ ఊర్థ్వ బలం విమానం బరువు కన్న ఎక్కువగా ఉంటుంది. అందువలన విమానం గాలిలో పైకి ఎగురగల్గుతుంది.

ప్రశ్న 11.
తలతన్యతను మరియు ఉపరితల శక్తిని వివరించండి. [Imp.Q][Mar 13]
జవాబు:
తలతన్యత :
సమతాస్థితిలో ఉన్న ఒక స్వేచ్ఛాతలంపై ఒక ఊహారేఖకు ఇరువైపులా రేఖకు లంబంగా ప్రమాణ పొడవు పై తలానికి స్పర్శియంగా పనిచేసే బలాన్ని తలతన్యత అంటారు.

ఉపరితల శక్తి :
అణు ఆకర్షణ బలాల వల్ల ప్రమాణ ఉపరితల వైశాల్యం పొందిన అధిక స్థితిజశక్తిని ఉపరితల శక్తి అంటారు.
తలతన్యతకు(T)ఉపరితల శక్తికి (W) మధ్య సంబంధం T = \(\frac{\mathrm{W}}{\Delta A}\)
∆A అనునది వైశాల్యంలోని పెరుగుదల.

ప్రశ్న 12.
ప్రయోగాత్మకంగా తలతన్యతను కనగొను విధానమును వివరించండి.
జవాబు:
ఒక ద్రవము యొక్క తలతన్యతను కనుగొను ప్రయోగము లోని పరికరముల అమరిక పటములో చూపినట్లు ఉండును. తలతన్యత కనుగొన వలసిన ద్రవమును ఒక పాత్రలో తీసుకుంటారు. ఒక త్రాసు యొక్క ఒక భుజము నుండి సమతల అంచు గల ఒక నిట్టనిలువు గాజు పలకను నిట్టనిలువుగా పాత్రలోని ద్రవమునకు కొంచెముపైన ఉండునట్లు అమరుస్తారు. దీని కోసం త్రాసు రెండవ భుజము నుండి వ్రేలాడదీసిన పళ్ళెములోని బరువులు ఉపయోగపడతాయి.

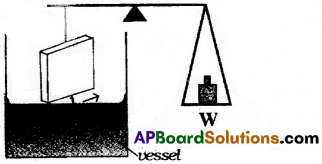
గాజు పలకను ద్రవ ఉపరితలము తాకునట్లుగా పాత్రను కొంచెం పైకి జరుపుతారు. తలతన్యత వలన గాజు పలక కొంచెం క్రిందికి లాగబడును. గాజుపలక ద్రవ ఉపరితలము నుండి కేవలము పైకి వచ్చుటకు కావలసిన బరువులను రెండవ వైపు పళ్ళెములో వేయవలయును. వేసిన భారము W అయిన ద్రవము తలతన్యతను ఈ క్రింది సూత్రము ద్వారా కనుగొనవచ్చును
తలతన్యత, S = \(\frac{W}{2l}=\frac{mg}{2l}\)

‘m’ అనునది పళ్ళెములో వేసిన అధిక ద్రవ్యరాశి మరియు ‘l’ అనునది గాజు పలక అంచు యొక్క పొడవు.

Long Answer Questions (దీర్ఘ సమాధాన ప్రశ్నలు)

ప్రశ్న 1.
బెర్నౌలీ సిద్ధాంతాన్ని నిర్వచించండి. గొట్టంలో ప్రవహిస్తున్న ద్రవానికి శక్తి నిత్యత్వ సూత్రం ద్వారా బెర్నౌలి సిద్ధాంతంను ఉత్పాదించండి. బెర్నౌలి సిద్ధాంతానికి ఒక అనువర్తనాన్ని వివరించండి.
జవాబు:
బెర్నౌలి సిద్ధాంతం :
ఒక గొట్టంలో, నిలకడరీతిలో ప్రవహిస్తున్న అసంపీడ్య, స్నిగ్ధతలేని ప్రవాహంలో, ఏకాంక ఘనపరిమాణం గల ప్రవాహి పీడనశక్తి, గతిజశక్తి, స్థితిశక్తి ఏ బిందువు వద్దనైనా స్థిరం.
బెర్నౌలి సమీకరణం P + ρgh + = \(\frac{1}{2}\)ρv² = స్థిరం

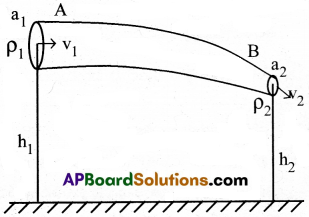
పటంలో చూపిన విధంగా స్నిగ్ధతలేని అసంపీడ్య ప్రవాహం నిలకడ రీతిలో ఒక గొట్టంలో ప్రవహిస్తుంది. ఈ గొట్టం A వైపు అడ్డుకోత వైశాల్యం, a₁ కలిగి, h₁ ఎత్తులో, v₁ వేగంతో ప్రవాహి ప్రవేశించి, గొట్టం చివర B వద్ద అడ్డుకోత వైశాల్యం a₂ కలిగి, h₂ ఎత్తులో v₂ వేగంతో ద్రవం బహిర్గతమవుతుంది.

గొట్టంలో ప్రవేశించే ప్రవాహి ద్రవ్యరాశి = గొట్టం నుండి బహిర్గతమయ్యే ప్రవాహి ద్రవ్యరాశి.
⇒ m = ρ₁a₁ v₁dt = ρ₂a₂v₂dt
ప్రవాహి అసంపీడ్యమైతే ⇒ ρ₁ = ρ₂ = ρ

i) గతిక ఉత్థాపన :
ఒక ప్రవాహిలో గమనంలో ఉన్న వస్తువుపై పనిచేసే ఊర్ధ్వ బలాన్నే గతిక ఉత్థాపన అంటారు.

ii) విమానం రెక్కలపై గతిక ఉత్థాపనం :
విమానం రెక్క మధ్యచ్ఛేద ఆకారంలో రెక్క క్రింది వైపు పుటాకార ఆకారాన్ని కలిగి ఉంటుంది.

బెర్నౌలీ సమీకరణం ప్రకారం పై తలం మీద తక్కువ పీడనం, దిగువ తలం మీద ఎక్కువ పీడనం ఉండడం వల్ల ఏర్పడిన పీడన వ్యత్యాసం విమానానికి కావలసిన ఉత్థాపనాన్ని కలిగిస్తుంది.

iii) భ్రమణంలో ఉన్న బంతిపై గతిక ఉత్థాపన :
ఒక బంతి గాలిలో కొంత వేగంతో (v) ప్రయాణిస్తుంటే, ఆత్మభ్రమణం వలన దాని చుట్టూ ధారారేఖలు ఏర్పడతాయి.

బెర్నౌలీ సిద్ధాంతం ప్రకారం, ప్రవాహి యొక్క వేగం పెరిగితే, అక్కడ పీడనం తగ్గుతుంది. వేగం తగ్గితే పీడనం పెరుగుతుంది. ఈ వేగాల తేడా వల్ల బంతిపై పనిచేసే ఫలిత ఊర్ధ్వబలాన్ని గతిక ఉత్థాపనం అంటారు.

ప్రశ్న 2.
స్నిగ్ధతా గుణకమును నిర్వచించండి. స్ట్రోక్ నియమమును వివరించి ఒక వాన బిందువు ఏ పరిస్థితులలో చరమ లేక అంత్య వేగమును పొందుతుందో వివరించండి. అంత్య వేగానికి సమీకరణమును వ్రాయండి.
జవాబు:
స్నిగ్ధతా :
ప్రవాహిలో ప్రవాహి పొరల మధ్య సాపేక్ష గమనాన్ని నిరోధించే ధర్మాన్నే స్నిగ్ధత అంటారు.

స్నిగ్ధతా గుణకం :
ప్రవాహి దిశకు లంబంగా పొరల మధ్య ఏకాంక వేగ ప్రవణత ఉన్నప్పుడు ఏకాంక వైశాల్యం గల పొరల మీద పనిచేసే స్నిగ్ధతా బలపరిమాణమే స్నిగ్ధతాగుణకం.

స్టోక్ నియమం :
ప్రవాహిలో క్రిందికి పడుతున్న నునుపైన గోళాకారపు వస్తువుపై పనిచేసే నిరోధక బలం క్రింది వాటిపై ఆధారపడుతుంది.
i) ప్రవాహి యొక్క స్నిగ్ధతా గుణకం (η)
ii) గోళాకారపు వస్తువు వ్యాసార్ధం (r)
iii) ప్రవాహిలో వస్తువు వేగం(v)
అనగా F_v ∝ ηrV ⇒ F_v = kηrv.
ప్రయోగ పూర్వకంగా ‘k’ విలువ 6π గా కనుగొనబడింది.
∴ F_v = 6π ηrv

చరమ వేగం (V_t):
ఏదైనా ప్రవాహిలో ఒక వస్తువును స్వేచ్ఛగా జారవిడిస్తే అది ఆ ద్రవంలో కొంతదూరం ప్రయాణించి ఆ తరువాత స్థిరవేగాన్ని పొందుతుంది. ఆ స్థిరవేగాన్ని అంత్యవేగం లేక చరమ వేగం అంటారు.

అంత్యవేగానికి సమీకరణం :
‘r’ వ్యాసార్ధం ‘ρ’ సాంద్రత గల ఒక గోళము ρ₀ సాంద్రతగల ప్రవాహి గుండా ప్రయాణిస్తున్నప్పుడు దానిపై పనిచేసే బలాలు

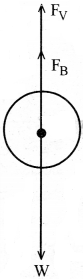
‘m’ అనునది గోళము ద్రవ్యరాశి.
గోళము యొక్క వేగము పెరుగుచున్న కొలది స్నిగ్ధతా బలం F_v పెరుగుచుండును.
ఒకానొక F_v విలువ వద్ద, W = F_B + F_v అగును.

అపుడు గోళము పై పనిచేయు ఫలిత బలము శూన్యమగును. గోళము స్థిర వేగముతో ప్రయాణించుట ఆరంభించును. ఈ స్థిర వేగమునే చరమ వేగము (V_T) అని అంటారు.

Solved Problems (సాధించిన సమస్యలు)

ప్రశ్న 1.
సరస్సు తలమునకు 10 మీటర్ల లోతులో ఉన్న ఈతగాని పై మొత్తము పీడనం ఎంత? (Take g = 10ms^-2)
సాధన:
మొత్తము పీడనం, P = వాతావరణ పీడనం + నీరు కలుగజేయు పీడనం P = P_a + ρgh
ఇక్కడ P_a = 1.01 × 10⁵ Pa, h= లోతు = 10m, ρ = నీటి సాంద్రత = 1000 కి. గ్రామీ^-3 g = 10 మీసె^-2.
P = 1.01 × 10⁵ + 1000 × 10 × 10 = 2.01 × 10⁵ Pa ≅ 2 అట్మాస్పియర్

ప్రశ్న 2.
సముద్ర మట్టము వద్ద వాతావరణ (గాలి) సాంద్రత 1.29 kg/m³ ఎత్తునకు వెళ్ళినప్పటికి సాంద్రత విలువలో మార్పు లేదు అని అనుకొనిన, ఎంత ఎత్తు వరకు వాతావరణము ఉండును?
సాధన:
P_a = ρgh. ఇక్కడ వాతావరణ పీడనం, P_a = 1.01 × 10⁵ Pa, g = 9.8 మీ సె^-2, ρ = 1.29 కి. గ్రామీ^-3
1.01 × 10⁵ = 1.29 × 9.8 × h

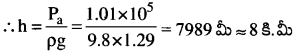
ప్రశ్న 3.
రెండు సిరంజిల మధ్యచ్ఛేద వైశాల్యములు A₁, A₂ మరియు పొడవులు L₁, L₂ (సూదులు లేకుండా). వీనిని నీటితో నింపి ఒక రబ్బరు గొట్టముతో బిగుతుగా ఈ రెండింటిని కలిపిరి. వీనిపై ఉన్న ముషలకములలో చిన్నదాని వ్యాసం 1.0సెం.మీ, పెద్ద దాని వ్యాసం 3.0 సె.మీ అయిన (a) చిన్న ముషలకముపై 10 N బలం ప్రయోగించిన పెద్ద ముషలకముపై ప్రయోగింపబడు బలం ఎంత? (b)చిన్న ముషలకమును 6.0 సె.మీ లోపలికి నెట్టిన, పెద్ద ముషలకము బయటకు ఎంత దూరము జరుగును?
సాధన:

ప్రశ్న 4.
కార్లను పైకి లేపు లిఫ్టు వంటి పరికరములో 5.0 సెం.మీ వ్యాసార్థము గల చిన్న ముషలకముపై సంపీడ్యము చెందించిన గాలి F₁ అను బలమును ప్రయోగించును. పైకి లేపవలసిన కారు ద్రవ్యరాశి 1350కి.గ్రా అది 15 సెం.మీ వ్యాసార్థముగల ముషలకము పై ఉన్నది. అయిన F₁ విలువ ఎంత ఉండవలయును? g = 9.8 ms^-2 అయిన ఈ పని చేయుటకు కావలసిన పీడనం ఎంత?
సాధన:
పాస్కల్ నియమం ప్రకారం, ఒక ప్రవాహిలో పీడనం మార్పు లేకుండా ఒక చోటు నుండి వేరొక చోటునకు ప్రసారమగును. అనగా చిన్న ముషలకం వద్ద పీడనం = పెద్ద ముషలకం వద్ద పీడనం
ఇది దాదాపు వాతావరణ పీడనమునకు రెట్టింపు.

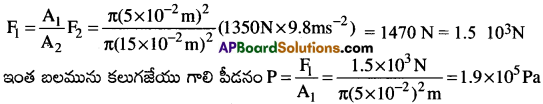
Exercise Problems

ప్రశ్న 1.
తలతన్యత బలమునకు వ్యతిరేకముగా 0.6 సెం.మీ వ్యాసము గల సబ్బు బుడగను ఊదుటకు చేయవలసిన పని ఎంత? (సబ్బు నీటి తలతన్యత = 2.5 × 10^-2 Nm^-1)
సాధన:
సబ్బు నీటి తలన్యత S = 2.5 × 10^-2 Nm^-2
సబ్బు బుడగ వ్యాసము = 0.6cm = 0.6 × 10^-2m
⇒ సబ్బు బుడగ వ్యాసార్థము r = 0.3 × 10^-2m.
సబ్బు బుడగను ఊదుటకు చేసిన పని W = 8πr²S = 8 × 3.14 ×(0.3 × 10^-2)² × 2.5 × 10^-2 = 5.652 × 10^-6 Joule.

ప్రశ్న 2.
0.06 సెం.మీ వ్యాసము గల గాజు గొట్టము లో ఎంత ఎత్తు వరకు మీథైల్ ఆల్కహాల్ ఎగబ్రాక గలదు? మీథైల్ ఆల్కహాల్ తలతన్యత = 0.023 Nm^-1 మీథైల్ ఆల్కహాల్ సాంద్రత = 0.8 gmcm^-3 స్పర్శ కోణము = 0°
సాధన:

ప్రశ్న 3.
ఒక కేశనాళికలో 6 సెం.మీ ఎత్తునకు నీరు ఎగబ్రాగుటకు కేశనాళిక వ్యాసార్థము ఎంత ఉండవలయును? నీటి తలతన్యత = 7.2 × 10^-2N/m, g = 10m/sec², స్పర్శ కోణము = 0°
సాధన:

ప్రశ్న 4.
0.4 మి.మీ వ్యాసముగల కేశనాళికను పాదరసము గల బీకరులో ముంచిన కేశనాళికలో పాదరసపు అవరోహణ ఎంత? పాదరసము సాంద్రత = 13.6 × 10³kg m^-3, తలతన్యత 0.49 Nm^-1 స్పర్శకోణం 135°
సాధన:

θ = 135° అందువలన h ఋణాత్మకముగా ఉండును. అనగా కేశనాళికలోని పాదరస మట్టము బీకరులోని పాదరస మట్టము ఉన్న తక్కువగా ఉండును.
పాదరస సాంద్రత p = 13.6 × 10³ kg/m³, కేశనాళిక వ్యాసార్థం a = 0.2 × 10^-3m,
పాదరస తలతన్యత S = 0.49 Nm^-1, స్పర్శకోణం θ = 135°

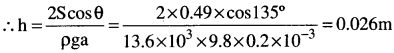
ప్రశ్న 5.
ఒక సబ్బు బుడగ వ్యాసము 10 మి.మీ మరియు దాని తలతన్యత 0.04 Nm^-1 అయిన బుడగలోని అధిక పీడనం ఎంత? [IPE ’14][TS 16,18][AP 15]
సాధన:

ప్రశ్న 6.
R వ్యాసార్థం గల బుడగను ఊదుటకు చేసిన పని W అయితే దాని వ్యాసార్థమును 2R చేయుటకు కావలసిన శక్తి ఎంత?
సాధన:
R వ్యాసార్థము గల సబ్బు బుడగను ఊదుటకు చేయవలసిన పని 8πR²S కు సమానం అనగా W = 8πR²S.
సబ్బు బుడగ వ్యాసార్ధమును r₁ నుండి r₂ కు పెంచుటకు చేయ వలసిన పని 2R = 8πS(r₂² – r₁²) ఇక్కడ r₁ = R మరియు r₂ = 2R కనుక చేయువలసిన పని
= 8πS((2R)² – R²) = 3(8πR²S) = 3W

ప్రశ్న 7.
వ్యాసార్థములు R₁ మరియు R₂ గల రెండు సబ్బు బుడగలు శూన్యములో సమ ఉష్ణోగ్రత పరిస్థితులలో ఏకమై ఒక సబ్బు బుడగ ఏర్పడిన దాని వ్యాసార్థము ఎంత? సబ్బు నీటి తలతన్యత T అనుకొనుము.
సాధన:
R₁ వ్యాసార్థము గల సబ్బు బుడగను ఊదుటకు చేయవలసిన పని = R₁ = W₁ = 8πR₁²T
R₂ వ్యాసార్ధము గల సబ్బు బుడగను ఊదుటకు చేయవలసిన పని R₂ = W₂ = 8πR₂²T
మొత్తము పని W = W₁ + W₂ = 8πR₁²T + 8πR₂²T = 8π(R₁² + R₂²)T
రెండు సబ్బు బుడగలు ఏకమైన తరువాత ఏర్పడిన సబ్బు బుడగ వ్యాసార్థం R అయితే దానిని ఊదుటకు చేయవలసిన పని W = 8πR²T