AP Inter 1st Year Maths 1B Question Paper May 2019

Access to a variety of AP Inter 1st Year Maths 1B Model Papers and AP Inter 1st Year Maths 1B Question Paper May 2019 allows students to familiarize themselves with different question patterns.

AP Inter 1st Year Maths 1B Question Paper May 2019

Time : 3 Hours
Max. Marks : 75

Section – A
(10 × 2 = 20)

I. Very Short Answer Type Questions.

1. Answer all questions.
2. Each question carries two marks.

Question 1.
Find the ratio in which the straight line 3x + 4y = 6 divides the line joining the points (2, -1) and (1, 1). State whether the points lie on the same side or on either side of the straight line.
Solution:
Let L ≡ 3x + 4y – 6 = 0
L₁₁ = 3(2) + 4(-1) – 6
= 6 – 4 – 6
= – 4
L₂₂ = 3(1) + 4(1) – 6
= 3 + 4 – 6
= 1
∴ The straight line L = 0 divides the line joining the points (2, -1) and (1, 1) in the ratio -L₁₁ : L₂₂
= -(-4) : 1
= 4 : 1
L₁₁ and L₂₂ have the opposites sign, the two points lie on the opposite side of the given tine L = 0.

Question 2.
Find the value of p, if the straight lines 3x + 7y – 1 =0 and 7x – py + 3 = 0 are mutually perpendicular.
Solution:
Given straight line equations are
3x + 7y – 1 = 0 ……. (1)
7x – py + 3 = 0 ……. (2)
Since (1), (2) are mutually perpendicular
∴ a₁a₂ + b₁b₂ = 0
⇒ 3(7) + 7(-p) = 0
⇒ 21 – 7p = 0
⇒ 7p = 21 ⇒ p = 3.

Question 3.
Show that the points A(3, 2, -4), B(5, 4, – 6) and C(9, 8, -10) are collinear and find the ratio in which B divides AC.
Solution:
Given A = (3, 2, – 4)
B = (5, 4, -6)
C = (9, 8, -10)

∴ A, B, C are collinear.
B divides AC in the ratio = AB: BC
= 2\(\sqrt{3}\) + 4\(\sqrt{3}\)
= 1 : 2

Question 4.
Find the equation to the plane parallel to the ZX – plane and passing through (0, 4, 4).
Solution:
The equation to the plane parallel to ZX – plane and passing through (x₁, y₁, z₁) is y = y₁
∴ The equation to the plane parallel to ZX -p lane and passing through (0, 4, 4) is y = 4.

Question 5.
Show that: \(\lim _{x \rightarrow 2} \frac{|x-2|}{x-2}\) = -1.
Solution:

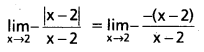
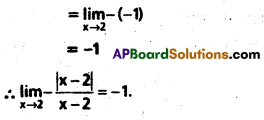
Question 6.
Compute \(\lim _{x \rightarrow-\infty} \frac{5 x^3+4}{\sqrt{2 x^4+1}}\)
Solution:

Question 7.
If f(x) = cos [log (cot x)], then find f(x).
Solution:
Given f(x) = cos [log(cot x)]
Differentiating w.r.to ‘x’ on both sides
f(x) = – sin[log(cot x)]. \(\frac{d}{d x}\)[log(cot x)]
= -sin[log(cot x)]. \(\frac{1}{\cot x} \cdot \frac{d}{d x}\)(cot x)
= – sin[log(cot x)]. \(\frac{1}{\cot x}\)(- cosec² x)
= sin[log(cot x)]. \(\frac{\sin x}{\cos x} \cdot \frac{1}{\sin ^2 x}\)
= \(\frac{2 \sin [\log (\cot x)]}{2 \sin x \cos x}\) = \(\frac{2 \sin [\log (\cot x)]}{\sin 2 x}\)

Question 8.
If f(x) = 2x² + 3x – 5, then prove that f(0) – 3f'(-1) = 0.
Solution:
Given f(x) = 2x² + 3x – 5
f (x) = 4x + 3
f'(0) = 4(0) + 3 = 3
f'(-1)= 4(-1) + 3 = – 4 + 3 = – 1
∴ f'(0) + 3f'(-1) = 3 + 3(-1) = 3 – 3 = 0
∴ f'(0) + 3f'(-1) = 0.

Question 9.
The time t, of a complete oscillation of a simple pendulum of length l is given by t = 2π\(\sqrt{\frac{l}{\mathrm{~g}}}\) where g is gravitational constant. Find the approximate percentage of error in t when the percen tage of error in l is 1%.
Solution:

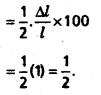
Question 10.
Define stationary point with example.
Solution:
Stationary point: A point x = c in the domain of the function is said to be a stationary point of y = f(x) if f(c) = 0.

Section – B
(5 × 4 = 20)

II. Short answer type questions:

1. Attempt ANY FIVE questions.
2. Each question carries FOUR marks.

Question 11.
Find the equation of locus of P, if the line segment joining (2, 3) and (-1, 5) subtends a right angle at P.
Solution:
Let A = (2, 3), B = (-1, 5)
Let p(x₁, y₁) be any point on the locus.
Given geometric condition is PA² + PB² = AB²

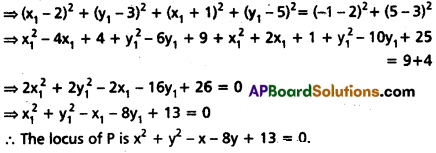
Question 12.
When the origin is shifted to the point (2, 3), the transformed equation of a curve is : x² + 3xy – 2y² + 17x – 7y – 11 = 0. Find the original equation of the curve.
Solution:
Equations of transformation are x = x’ + h, y = y’ + k
x’ = x – h = x – 2, y’ = y – 3
Transformed equation is x² + 3xy – 2y² + 17x – 7y – 11 = 0
Original equation is (x – 2)² + 3(x – 2) (y – 3) – 2 (y – 3)² + 17(x – 2) – 7(y – 3) – 11 = 0
x² – 4x + 4 + 3xy – 9x – 6y + 18 – 2y² + 12y – 18 + 17x – 34 – 7y + 21 – 11 = 0
x² + 3xy – 2y² + 4x – y – 20 = 0
This is the required original equation.

Question 13.
A straight line passing through A(1, -2) makes an angle tan^-1\(\left(\frac{4}{3}\right)\) with the positive direction of the X-axis in the anticlockwise sense. Find the points on the straight line whose distance from A is 5.
Solution:
The parametric equations of the line through A(1, -2) and whose slope is \(\frac{4}{3}\) (∵ tanθ = \(\frac{4}{3}\)) are
x = 1 + r cosθ and y = -2 + r sinθ
x = 1 + r(\(\frac{3}{5}\)) and y = -2 + r(\(\frac{4}{5}\))
The points on the above line at a distance of |r| = 5
⇒ r = ± 5
If r = 5 then x = 1 + 5(\(\frac{3}{5}\)) and y = -2 + 5(\(\frac{4}{5}\))
x = 4 and y = 2
If r = -5 then x = 1 – 5(\(\frac{3}{5}\)) and y = -2 – 5(\(\frac{4}{5}\))
x = – 2 and y = – 6
Hence required points are (4, 2) and (-2, – 6).

Question 14.
Check the continuity of the following function at 2:

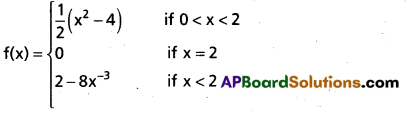
Solution:

Question 15.
Find the derivative of f(x) = cot x using the first principle.
Solution:
Let f(x) = cot x

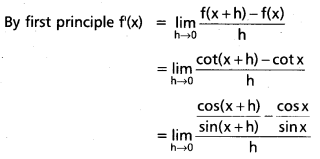
Question 16.
A stone is dropped into a quiet lake and ripples move in circles at the speed of 5 cm/sec. At the instant when the radius of circular ripple is 8 cm, how fast is the enclosed area increases ?
Solution:
Let r, A be the radius, area of a circular ripple.
Given \(\frac{\mathrm{dr}}{\mathrm{dt}}\) = 5 cm/sec. dt
A = πr²
\(\frac{\mathrm{dA}}{\mathrm{dt}}\) = \(\pi \cdot 2 \mathrm{r} \cdot \frac{\mathrm{dr}}{\mathrm{dt}}\)
When r = 8
\(\frac{\mathrm{dA}}{\mathrm{dt}}\) = π.2(5).8
= 80 π cm²/sec.
∴ The enclosed area increases 80 π cm²/sec.

Question 17.
Find the angle between the curves y² = 8x; 4x² + y² = 32.
Solution:
Given curve equations are y² = 8x ….. (1)
4x² + y² = 32 …… (2)
From (1) and (2)
4x² + 8x = 32
⇒ 4x² + 8x – 32 = 0
⇒ x² + 2x – 8 = 0
⇒ (x + 4) (x – 2) = 0
⇒ x = -4, x = 2
If x = 2 then y = ±4.
∴ The points of intersection of (1) and (2) are (2, 4) and (2, – 4)

Section – C

III. Long Answer type questions:

1. Attempt ANY FIVE questions.
2. Each question carries SEVEN marks.

Question 18.
Find the equations of the straight lines passing through the point (1, 2) and making an angle of 60° with the line \(\sqrt{3}\)x + y + 2 = 0.
Solution:
Let m be the slope of the required straight line Slope of the line \(\sqrt{3}\)x + y + 2 = 0 is –\(\sqrt{3}\)
Since the required straight line makes an angle of 60° with the line \(\sqrt{3}\)x + y + 2 = 0.

∴ The equation of the straight line passing through the point (1, 2) with slope \(\sqrt{3}\) is
y – 2 = \(\sqrt{3}\)(x – 1)
The equation of the straight line passing through the point (1, 2) with slope ‘o’ is
y – 2 = 0(x – 1) ⇒ y – 2 = 0
Hence required straight line equations are y – 2 = \(\sqrt{3}\)(x – 1) and y – 2 = 0.

Question 19.
Find the centroid and the area of the triangle formed by the lines 3x² – 4xy + y² = 0, 2x – y = 6.
Solution:
Given 3x² – 4xy + y² = 0
⇒ 3x² – 3xy – xy + y² = 0
⇒ 3x(x – y) – y(x – y) = 0
⇒ (x – y) (3x – y) = 0
⇒ x – y = 0 ………… (1)
3x – y = 0 ……… (2)
2x – y – 6 = 0 …… (3)
The point of intersection of (1) and (2) is 0(0, 0)
Solving (2) & (3)

Question 20.
Show that the product of the perpendicular distances from the origin to the pair of straight lines represented by
ax² + 2hxy + by² + 2gx + 2fy + c = 0 is :
\(\frac{|c|}{\sqrt{(a-b)^2+4 b^2}}\)
Solution:
Let S ≡ ax² + 2hxy + by² + 2gx + 2fy + c = 0
Let S = 0 represent lines be l₁x + m₁y + n₁ = 0 …… (1)
l₂x + m₂y + n₂ = 0 …… (2)
Then ax² + 2hxy + by² + 2gx + 2fy + c = (l₁x + m₁y + n₁)(l₂x + m₂y + n₂)
Comparing the co-efficients of like terms on both sides, we have

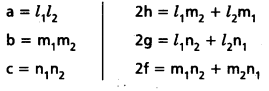
The perpendicular distance from origin to the line (1) = \(\frac{\left|\mathrm{n}_1\right|}{\sqrt{l_1^2+\mathrm{m}_1^2}}\)
The perpendicular distance from origin to the line (2) = \(\frac{\left|\mathrm{n}_2\right|}{\sqrt{l_2^2+\mathrm{m}_2^2}}\)
The product of the perpendicular distance from origin to the pair of straight lines

Question 21.
Find the angle between the lines whose direction cosines are given by the equations 3l + m + 5n = 0 and 6mn – 2nl + 5lm = 0.
Solution:
Given 3l + m + 5n = 0 …… (1)
6mn – 2nl + 5lm = 0 ……. (2)
From (1), m = – (3l + 5n)
Substituting in (2)
-6n(3l + 5n) – 2nl – 5l (3l + 5n) = 0
-18ln – 30n² – 2nl – 15l²– 25ln = 0
-15l² – 45ln – 30n² = 0
l² + 3ln + 2n² = 0
(l + 2n) (l + n) = 0
l + 2n = 0 or l + n = 0

Question 22.
Find the derivative of the function :
x^x + (cot x)^x.
Solution:
Let u = x^x and v = (cot x)^x
Let y = x^x + (cot x)^x
Then y = u + v
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = \(\frac{d u}{d x}+\frac{d v}{d x}\) ……. (1)
Taking logarithms on both sides, we have
log u = x log x
Differentiating w.r.to (x) on both sides, we have

Taking logarithms on bothsides, we have
log v = x log (cot x)
Differentiating w.r.to ‘x’ on both sides, we have

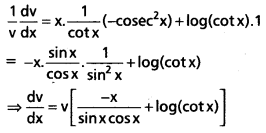
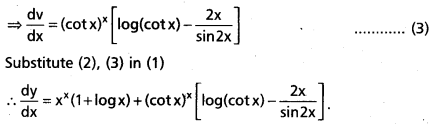
Question 23.
Find the equations of the tangents to the curve y = 3x² – x³, where it meets the X – axis.
Solution:
Given curve equation is y = 3x² – x³
y = 0 ⇒ 3x² – x³ = 0
⇒ x² (3 – x) = 0
⇒ x = 0, 3
∴ The curve crosses the x – axis at 0(0, 0) and A(3, 0)
y = 3x² – x³ ⇒ \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 6x – 3x²
\(\left(\frac{d y}{d x}\right)_{(0,0)}\) = 0 – 0 = 0
Equation of the tangent at 0(0, 0) is
y – 0 = 0(x – 0) ⇒ y = 0
y = 3x² – x³ ⇒ \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 6x – 3x²
\(\left(\frac{d y}{d x}\right)_{(3,0)}\) = 18 – 27 = -9
Equation of the tangent at A(3, 0) is
y – 0 = – 9(x – 3)
y = – 9x + 27
⇒ 9x + y = 27
Hence required tangent equations are y = 0 and 9x + y = 27.

Question 24.
From a rectangular sheet of dimensions 30 cm × 80 cm, four equal squares of side x cm are removed at the corners, and the sides are then turned up so as to form an open rectangular box. Find the value of x, so that the volume of the box is the greatest.
Solution:
Length of the box = 80 – 2x = l
Breadth of the box = 30 – 2x = b
Height of the box = x = h

Volume = lbh
= (80 – 2x) (30 – 2x). x
= x(2400 – 220x + 4x²)
f(x) = 4x³ – 220x² + 2400x
f(x) = 12x² – 440x + 2400
= 4[3x² – 110x + 600]
f(x) = 0 ⇒ 3x² – 110x + 600 = 0
x = \(\frac{110 \pm \sqrt{12100-7200}}{6}\)
= \(\frac{110 \pm 70}{6}\) = \(\frac{180}{6}\) or \(\frac{40}{6}\) = \(\frac{30}{3}\) or \(\frac{20}{6}\)
If x = 30,
b = 30 – 2x
= 30 – 2(30)
= -30 < 0
⇒ x ≠ 30
∴ x = \(\frac{20}{3}\)
f'(x) = 24x – 440
When x = \(\frac{20}{3}\) f”(x) = 24.\(\frac{20}{3}\) – 440
= 160 – 440
= -280 < 0
f(x) is maximum when x = \(\frac{20}{3}\)
Volume of the box is maximum when x = \(\frac{20}{3}\) cm.