AP Inter 1st Year Maths 1B Question Paper March 2019

Access to a variety of AP Inter 1st Year Maths 1B Model Papers and AP Inter 1st Year Maths 1B Question Paper March 2019 allows students to familiarize themselves with different question patterns.

AP Inter 1st Year Maths 1B Question Paper March 2019

Time : 3 Hours
Max. Marks : 75

Section – A
(10 × 2 = 20)

I. Very Short Answer Type Questions.

1. Answer all questions.
2. Each question carries two marks.

Question 1.
Find the angle which the straight line y = x – 4 makes with the y-axis.
Solution:
Given straight line is y = \(\sqrt{3}\)x – 4
m = \(\sqrt{3}\) ⇒ tan θ = \(\sqrt{3}\)
⇒ θ = 60°
The straight line y = \(\sqrt{3}\)x – 4 makes angle with the Y – axis is 90° – 60° = 30°.

Question 2.
Find the distance between the parallel straight lines 3x + 4y – 3 = 0 and 6x + 8y – 1 =0.
Solution:
Given straight lines are 3x + 4y – 3 = 0
⇒ 6x + 8y – 6 = 0 ……. (1)
6x + 8y – 1 = 0 ……… (2)
∴ The distance between the parallel straight lines.
(1) and (2) is \(\frac{\left|c_2-c_1\right|}{\sqrt{a^2+b^2}}\)
= \(\frac{|-1-(-6)|}{\sqrt{36+64}}\) = \(\frac{|-1+6|}{\sqrt{100}}\)
= \(\frac{5}{100}\) = \(\frac{1}{2}\)

Question 3.
Find ‘x’, if the distance between (5, -1, 7) and (x, 5, 1) is 9 units.
Solution:
Let A = (5, -1, 7)
B = (x, 5, 1)
Given AB = 9
⇒ \(\sqrt{(x-5)^2+(5+1)^2(1-7)^2}\) = 9
⇒ (x – 5)² + 36 + 36 = 81
⇒ (x – 5)² = 9
⇒ x – 5 = ±3
⇒ x – 5 = 3 (or) x – 5 = -3
⇒ x = 8 (or) x = 2.

Question 4.
Write the equation of the plane 4x – 4y + 2z + 5 = 0 in the intercept form.
Solution:
Given plane equation is 4x – 4y + 2z + 5 = 0
⇒ 4x – 4y + 2z = – 5
⇒ \(\frac{4 x}{-5}-\frac{4 y}{-5}+\frac{2 z}{-5}\) = 1
⇒ \(\frac{x}{-5 / 4}+\frac{y}{5 / 4}+\frac{z}{-5 / 4}\)
x- intercept = \(\frac{-5}{4}\)
y – intercept = \(\frac{5}{4}\)
z – intercept = \(\frac{-5}{2}\)

Question 5.
Compute \(\lim _{x \rightarrow 0} \frac{e^{3+x}-e^3}{x}\)
Solution:

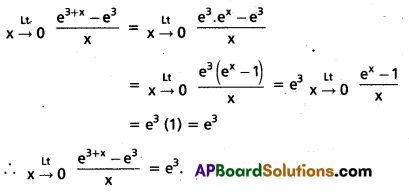
Question 6.
Compute \(\lim _{x \rightarrow 3} \frac{x^2+3 x+2}{x^2-6 x+9}\)
Solution:

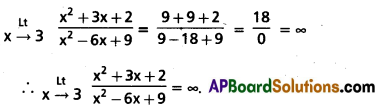
Question 7.
Find the derivative of the function tan^-1 (log x).
Solution:
Let y = tan^-1 (logx)
differentiating with respect to ‘x’ on both sides, we have

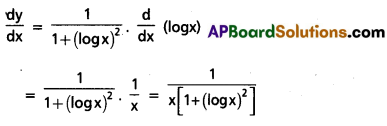
Question 8.
If y = \(\frac{2 x+3}{4 x+5}\) then find y”.
Solution:
Given y = \(\frac{2 x+3}{4 x+5}\)
differentiating with respect to x on both sides, we have

Question 9.
Define relative error and percentage error of the variable y.
Solution:
Relative error in y = \(\frac{\Delta y}{y}\)
Percentage error in y = \(\frac{\Delta y}{y}\) × 100

Question 10.
Find the absolute extremum of f(x) = x² defined on [-2, 2].
Solution:
Given f(x) = x² defined on [-2, 2]
Clearly f is continuous on [-2, 2].
It can be shown that it has only local minimum and the point of local minimum is 0.
∴ The absolute maximum of f is the largest value of f(-2), f(0) and f(2)
f(-2) = (-2)² = 4
f(0) = 0² = 0
f(2) = 2² = 4.
∴ The absolute maximum value is 4.
similarly the absolute minimum is the least value of 4, 0, 4.
∴ The absolute minimum value is 0.

Section – B

II. Short Answer Type Questions.

1. Attempt any five questions.
2. Each question carries four marks.

Question 11.
A (5, 3) and B (3, -2) are two fixed points. Find the equation of locus of P, so that the area of triangle PAB is 9.
Solution:
Given A = (5, 3)
B = (3, – 2)
Let P(x₁, y₁) be any point on the locus.
Given geometric condition is area of ∆PAB is 9.
⇒ \(\frac{1}{2}\left|\begin{array}{cccc}
x_1 & 5 & 3 & x_1 \\
y_1 & 3 & -2 & y_1
\end{array}\right|\) = 9

Question 12.
When the origin is shifted to the point (3, -4) and transformed equation is x + y² = 4. Find the original equation.
Solution:
Here (h, k) = (3, -4)
we know x = x + h ⇒ x = x – h
⇒ x = x – 3
y = y + k ⇒ y = y – k
⇒ y = y – (-4)
⇒ y = y + 4
Given transformed equation is x² + y² = 4
⇒ (x – 3)² + (y + 4)² = 4
⇒ x² – 6x + 9 + y² + 8y + 16 = 4
⇒ x² + y² – 6x + 8y + 21 = 0.
∴ Required original equation is x² + y² – 6x + 8y + 21 = 0.

Question 13.
If the straight lines ax + by + c = 0, bx + cy + a = 0 and cx + ay + b = 0 are concurrent, then prove that a³ + b³ + c³ = 3 abc.
Solution:
Given ax + bc + c = 0 ……… (1)
bx + cy + a = 0 ……… (2)
cx + ay + b = 0 ……… (3)
solving (1) and (2)

Question 14.
Compute \(\lim _{x \rightarrow a}\left(\frac{x \sin a-a \sin x}{x-a}\right)\)
Solution:

Question 15.
Find the derivative of the function cot x from the first principle.
Solution:
Let f'(x) = cot x
f (x + h) = cot (x + h)
By first principle

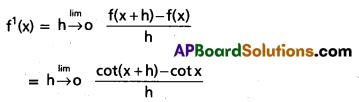
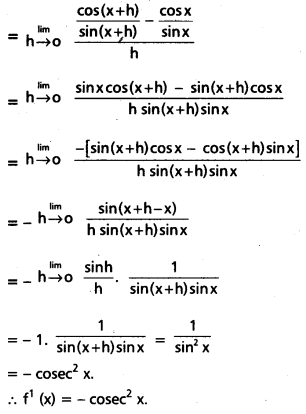
Question 16.
Find the approximate value of \(\sqrt[3]{999}\).
Solution:
Let f (x) = x^1/3, x = 1000, ∆x = – 1

Question 17.
The distance – time formula for the motion of a particle along a straight line is s = t³ – 9t² + 24t – 18. Find when and where the velocity is zero.
Solution:
Given s = t³ – 9t² + 24t – 18.
Velocity v = \(\frac{\mathrm{ds}}{\mathrm{dt}}\) = 3t² – 18t + 24t.
v = 0 ⇒ 3t² – 18t + 24t = 0
⇒ t² – 6t + 8 = 0
⇒ t² – 2t – 4t + 8 = 0
⇒ t (t – 2) – 4 (t – 2) = 0
⇒ (t – 2)(t – 4) = 0
t = 2 (or) t = 4.
When t = 2
s = 2³ – 9 (2)² + 24(2) – 18
= 8 – 36 + 48 – 18
= 56 – 54
= 2 units
When t = 4
s = 4³ – 9 (4)² + 24 (4) – 18
= 64 – 144 + 96 – 18
= 160 – 162 = 2 units.

Section – C

III. Long Answer Type Questions.

1. Attempt any five questions.
2. Each question carries seven marks.

Question 18.
If Q (h, k) is the image of the point P(x₁, y₁) with respect to the straight line ax + by + c = 0 then prove that \(\frac{h-x_1}{a}\) = \(\frac{k-y_1}{b}\) = \(\frac{-2\left(a x_1+b y_1+c\right)}{a^2+b^2}\)
Solution:
Let L ≡ ax + by + c = 0
Given Q (h, k) is the image of p(x₁, y₁)
with respect to the straight line L = 0.

⇒ a(h + x₁) + b(k + y₁) + 2c = 0
⇒ a(x₁ + aλ + x₁) + b(y₁ + b + y₁) + 2c = 0.
⇒ 2ax₁ + a²λ + 2by₁ + b²λ + 2c = 0.
⇒ (a² + b²)λ = -2(ax₁ + by₁ + c)
⇒ λ = \(\frac{-2\left(a x_1+b y_1+c\right)}{a^2+b^2}\)
from (1)
∴ \(\frac{h-x 1}{a}\) = \(\frac{k-y_1}{b}\) = \(\frac{-2\left(a x_1+b y_1+c\right)}{a^2+b^2}\)

Question 19.
If the equation S ≡ ax² + 2hxy + by² + 2gx + 2fy + c = 0 represents a pair of parallel straight lines then show that
(i) h² = ab
(ii) af² = bg² and
(iii) the distance between the parallel lines
= \(\sqrt[2]{\frac{g^2-a c}{a(a+b)}}\) = \(\sqrt[2]{\frac{f^2-a c}{b(a+b)}}\)
Solution:
Let the two parallel straight lines represented by S = 0 be
lx + my + n₁ = 0 ………… (1)
and lx + my + n₂ = 0 ……. (2)
Then, S ≡ λ(lx + my + n₁) (lx + my + n₂), for some real λ ≠ 0.
From this we have
l² = \(\frac{a}{\lambda}\), m² = \(\frac{b}{\lambda}\), n₁n₂ = \(\frac{c}{\lambda}\), lm = \(\frac{h}{\lambda}\)
l(n₁ + n₂) = \(\frac{2 \mathrm{~g}}{\lambda}\) and m(n₁ + n₂) = \(\frac{2 f}{\lambda}\).
Now

(i) h² = λ²l²m² = (λl²)(λm²) = ab.

(ii) 4af² = (λ²l²) (λ²m²) (n₁ + n₂)²
= (λm²) (λ²l²) (n₁ + n₂)² = b(4g²)
so that af² = bg².

(iii) Distance between the parallel lines

Question 20.
Find the value of k, if the lines joining the origin to the points of intersection of the curves 2x² – 2xy + 3y² + 2x – y – 1 =0 and the line x + 2y = k are mutually perpendicular.
Solution:

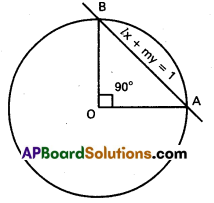
Equation of the circle is x² + y² = a² …… (1)
Equation of AB is lx + my = 1 ……….. (2)
Homogenising (1) with the help of (2)
Combined equation of OA, OB is
x² + y² = a².1²
x² + y² = a² (lx + my)²
= a²(l²x² + m²y² + 2lmxy)
= a²l²x² + a²m²y² + 2a²lmxy
i.e., a²l²x² + 2a² lmxy + a² m²y² – x² – y² = 0
(a²l² – 1) x² + 2a² lmxy + (a²m² – 1) y² = 0
Since OA, OB are perpendicular
Co-efficient of x² + co-efficient of y² = 0
a²l² – 1 + a²m² – 1 = 0
a²(l² + m²) = 2
This is the required condition.

Question 21.
Find the angle between the lines whose direction cosines satisfy the equations l + m + n = 0, l² + m² – n² = 0.
Solution:
Given l + m + n = 0 …… (1)
l² + m² – n² = 0 ……. (2)
From (1) l = – m – n …… (3)
Substituting in (2)
(- m – n)² + (m² – n²) = 0.
⇒ (m + n)² + (m + n) (m – n) = 0.
⇒ (m + n) [m + n + m – n] = 0
⇒ 2m (m + n) = 0
⇒ m = 0, m + n = 0
When m = 0
From (3), l = -n
∴ \(\frac{l}{l}\) = \(\frac{m}{0}\) = \(\frac{n}{-l}\)
When m = – n
From (3) l = -(-n) – n
= n – n
= 0.
∴ \(\frac{l}{0}\) = \(\frac{m}{l}\) = \(\frac{n}{-l}\)
∴ The d.rs of the two lines are (1, 0, -1) and (0, 1, -1) let ‘θ’ be the angle between the lines.

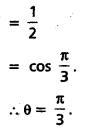
Question 22.
If y = x \(\sqrt{a^2+x^2}\) + a² log (x + \(\sqrt{a^2+x^2}\)) then prove that \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = \(2 \sqrt{a^2+x^2}\)
Solution:

Question 23.
Show that the condition for the orthogonality of the curves ax² + by² = 1 and a₁x² + b₁y² = 1 is \(\frac{1}{a}-\frac{1}{b}\) = \(\frac{1}{a_1}-\frac{1}{b_1}\).
Solution:
Let P(x₁, y₁) be the point of intersection of the curves
Given curve equation is ax² + by² = 1
Differentiating (1) w.r. to y on both sides, we have

Since ‘P’ lies on ax² + by² = 1 and a₁x² + b₁y² = 1
Solving these two equations, we get

Question 24.
Find the points of local extrema and local extrema for the function f(x) = cos 4x defined on \(\left(0, \frac{\pi}{2}\right)\)
Solution:
The function f(n) = cos 4x defined on (0, \(\frac{\pi}{2}\)) …….. (1)
f'(x) = – 4 sin 4x ……… (2)
f”(x) = -16 cos 4x …….. (3)
f'(x) = 0 ⇒ – 4 sin 4x = 0
⇒ sin 4x = 0.
⇒ 4x = 0, π, 2π, 3π, 4π, ….
⇒ x = 0, \(\frac{\pi}{4}\), \(\frac{\pi}{2}\), \(\frac{3 \pi}{4}\), π
Since x ∈ (0, \(\frac{\pi}{2}\))
∴ x = \(\frac{\pi}{4}\)
f”(\(\frac{\pi}{4}\)) = -16 cos 4 (\(\frac{\pi}{4}\))
= -16 cos π
= – 16 (-1)
= 16 > 0.
∴ The function f has local minimum at x = \(\frac{\pi}{4}\),
∴ Local minimum value = f(\(\frac{\pi}{4}\))
= cos 4(\(\frac{\pi}{4}\))
= cos π
= – 1.