AP Inter 1st Year Maths 1B Model Paper Set 3 with Solutions

by

Access to a variety of AP Inter 1st Year Maths 1B Model Papers Set 3 allows students to familiarize themselves with different question patterns.

AP Inter 1st Year Maths 1B Model Paper Set 3 with Solutions

Time : 3 Hours
Max. Marks : 75

Note : This question paper consists of three sections A, B and C.

Section-A
(10 × 2 = 20 Marks)

I. Very Short Answer Questions.

  1. Answer All questions.
  2. Each Question carries Two marks.

1. Find the slope of the line x + y = 0 and x – y = 0.

2. Transform the equation 3x + 4y + 12 = 0 into the intercept form.

3. Find the distance between (3, – 3, 2) and (1, 1, 1).

AP Inter 1st Year Maths 1B Model Paper Set 3 with Solutions

4. Find the equation of the plane. Whose intercepts on X, Y, Z – axes are 2, 3, 4 respectively.

5. Show that
AP Inter 1st Year Maths 1B Model Paper Set 3 with Solutions 2

6. Evaluate
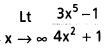
AP Inter 1st Year Maths 1B Model Paper Set 3 with Solutions 3

7. If f(x) = e2x. log x (x > 0), then find f(x).

8. If y = x2 ex sin x, find \(\frac{d y}{d x}\).

9. Find the approximate sin (62°).

10. Find the value of ‘C’ in Rolle’s theorem for the function
f(x) = x(x + 3)e-x/2 in [-3, 0].

Section – B
(5 × 4 = 20 Marks)

II. Short Answer Questions.

  1. Answer any Five questions.
  2. Each Question carries Four marks.

11. Find the locus of the third vertex of a right angled triangle, the ends of whose hypotenuse are (4, 0) and (0, 4).

12. The point to which the origin is shifted and the transformed equation are given below. Find the original equation.
(i) (3, -4); x2 + y2 = 4
(ii) (- 1, 2); x2 + 2y2 + 16 = 0.

13. If p and q are the lengths of the perpendiculars from the origin to the straight lines x sec α + y cosec α = a and x cos α – y sin α = a cos 2α, prove that 4p2 + q2 = a2.

14.
AP Inter 1st Year Maths 1B Model Paper Set 3 with Solutions 1

15. Find the derivative of tan 2x from the first principle.

AP Inter 1st Year Maths 1B Model Paper Set 3 with Solutions

16. The volume of a cube is increasing at the rate of 8 cm3/sec. How fast the surface area increasing when the length of an edge is 12 cm?

17. Find whether the curve y = f(x) = x2/3 has a vertical tangent at x = 0.

Section – C

III. Long Answer Questions.

  1. Answer any Five questions.
  2. Each Question carries Seven marks.

18. A straight line L with negative slope passes through the point (8, 2) and cuts positive co-ordinate axes at the points P and Q. Find the minimum value of OP + OQ as L varies when O is the origin.

19. Show that the product of the perpendicular distances from a point (α, β) to the pair of straight lines ax2 + 2hxy + by2 = 0 is \(\frac{\left|a \alpha^2+2 h \alpha \beta+b \beta^2\right|}{\sqrt{(a-b)^2+4 h^2}}\)

20. Show that the lines joining the origin to the points of intersection of the curve x2 – xy + y2 + 3x + 3y – 2 = 0 and the straight line x – y – \(\sqrt{2}\) = 0 are mutually perpendicular.

21. Find the direction cosines of two lines which are connected by the relations l + m + n = 0 and mn – 2nl – 2lm = 0.

22. If sin \(\left[\frac{2^{x+1}}{1+4^x}\right]\), then find \(\frac{d y}{d x}\).

AP Inter 1st Year Maths 1B Model Paper Set 3 with Solutions

23. Find the lengths of normal and sub-normal at a point on the curve y = \(\frac{a}{2}\left(e^{x / a}+e^{-x / a}\right)\).

24. A container in the shape of an inverted cone has height 12 cm and radius 6 cm at the top. If it is filled with water at the rate of 12 cm3/sec., What is the rate of change in the height of water level when the tank is filled 8 cm?

Leave a Comment