AP Inter 1st Year Maths 1B Model Paper Set 2 with Solutions

Access to a variety of AP Inter 1st Year Maths 1B Model Papers Set 2 allows students to familiarize themselves with different question patterns.

AP Inter 1st Year Maths 1B Model Paper Set 2 with Solutions

Time : 3 Hours
Max. Marks : 75

Note : This question paper consists of three sections A, B and C.

Section-A
(10 × 2 = 20 Marks)

I. Very Short Answer Questions.

1. Answer All questions.
2. Each Question carries Two marks.

1. Write the ratio in which the straight line 3x – 4y = 7 divides the line segment joining the points (2, – 7) and (-1, 3).

2. Transform the equation \(\sqrt{3}\)x + y + 10 = 0 into the slope intercept form.

3. Find the distance of P(3, – 2, 4) from the origin.

4. Suppose a plane makes intercepts 2, 3, 4 on the X, Y, Z – axes respectively. The equation of the plane whose X, Y, Z-intercepts ares a, b, c is \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\) = 1.

5. Compute

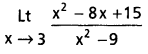
6. Find \(\begin{aligned}
& \text { Lt } \\
& x \rightarrow 1
\end{aligned}\) (x + 2) (2x + 1)

7. y = ae^nx + be^-nx then prove that y” = n²y.

8. If y = e^a sin^-1 x then prove that \(\frac{d y}{d x}\) = \(\frac{a y}{\sqrt{1-x^2}}\).

9. Find the approximate value of \(\sqrt{82}\).

10. Find the value of ‘C in Rolle’s theorem for the function f(x) = x² – 1 on [- 1, 1].

Section – B
(5 × 4 = 20 Marks)

II. Short Answer Questions.

1. Answer any Five questions.
2. Each Question carries Four marks.

11. Find the equation of the locus of P, if the ratio of the distances from P to A(5, – 4) and B(7, 6) is 2 : 3.

12. When the origin is shifted to the point (2, 3), the transformed equation of a curve is x² + 3xy – 2y² + 17x – 7y – 11 = 0. Find the original equation of the curve.

13. Find the value of ‘a’ if the distances of the points (2, 3) and (-4, a) from the straight line 3x + 4y – 8 = 0 are equal.

14. Find the real constant a, b so that the function f given by

15. Find the derivative of x sin x from the first principle.

16. If an error of 0.01 cm is made in measuring the perimeter of a circle and the perimeter is measured as 44 cm then find the approximate error and relative error in its area.

17. Find the equations of the tangent and the normal to the curve y⁴ = ax⁴, at (a, a).

Section – C
(5 × 7 = 35 Marks)

III. Long Answer Questions

1. Answer any Five Questions.
2. Each Question carries Seven marks.

18. Find the equation of straight lines passing through the point (1, 2) and making an angle 60° with the line \(\sqrt{3}\)x + y + 2 = 0.

19. Show that the lines represented by (lm + my)² – 3 (mx – ly)² = 0 and lx + my + n = 0 form an equilateral triangle with area \(\frac{\mathrm{n}^2}{\sqrt{3}\left(l^2+\mathrm{m}^2\right)}\).

20. Show that the straight lines represented by 3x² + 48xy + 23y² = 0 and 3x – 2y + 13 = 0 form an equilateral triangle of area \(\begin{aligned}
& 13 \\
& \sqrt{3}
\end{aligned}\) units.

21. Show that the lines whose direction cosines are given by l + m + n = 0, 2mn + 3nl – 5lm = 0 are perpendicular to each other.

22. If y = tan^-1\(\left[\frac{\sqrt{1+x^2}+\sqrt{1-x^2}}{\sqrt{1+x^2}-\sqrt{1-x^2}}\right]\) for 0 < |x| < 1, find \(\frac{d y}{d x}\)

23. At a point (x₁, y₁) on the curve x³ + y³ = 3axy, show that the tangent is (x² – ay₁) x + (\(y_1^2\) – ax₁)y = ax₁y₁.

24. If the curved surface of right circular a cylinder inscribed in a sphere of radius r is maximum, show that the height of the cylinder is \(\sqrt{2} \mathrm{r}\).