AP Inter 1st Year Maths 1B Model Paper Set 1 with Solutions

by

Access to a variety of AP Inter 1st Year Maths 1B Model Papers Set 1 allows students to familiarize themselves with different question patterns.

AP Inter 1st Year Maths 1B Model Paper Set 1 with Solutions

Time : 3 Hours
Max. Marks : 75

Note : This question paper consists of three sections A, B and C.

Section-A
(10 × 2 = 20 Marks)

I. Very Short Answer Questions.

  1. Answer All questions.
  2. Each Question carries Two marks.

1. Find the equation of the straight line passing through the points (1,-2) and (-2, 3).

2. Transform the equation x + y – 2 = 0 into the intercept form.

AP Inter 1st Year Maths 1B Model Paper Set 1 with Solutions

3. Show that the points (1, 2, 3) (7, 0, 1) and (-2, 3, 4) are collinear.

4. Find the intercepts of the plane 4x + 3y – 2z + 2 = 0 on the co-ordinate axes.

5. Show that
AP Inter 1st Year Maths 1B Model Paper Set 1 with Solutions 1

6. Compute
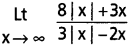
AP Inter 1st Year Maths 1B Model Paper Set 1 with Solutions 3

7. If f(x) = (ax + b)n, (x > \(-\frac{b}{a}\)), then find f'(x).

8. If y = log (cos h 2x), find \(\frac{\mathrm{dy}}{\mathrm{dx}}\).

9. Find the approximate value of 4\(\sqrt{17}\).

10. Find the value of ‘C’ in Lagrange’s mean value theorem f(x) = x2 on [2, 4].
Solution:

Section – B
(5 × 4 = 20 Marks)

II. Short Answer Questions.

  1. Answer any Five questions.
  2. Each question carries .Four marks.

11. Find the equation of locus of P, if A = (4, 0), B = (- 4, 0) and | PA – PB | =4.

12. When the origin is shifted to (3, 4) by the translation of axes, let us find the transformed equation of 2x2 + 4xy + 5y2 = 0.

AP Inter 1st Year Maths 1B Model Paper Set 1 with Solutions

13. Find the circumcentre of the triangle formed by the straight lines x + y = 0, 2x + y + 5 = 0 and x – y = 2.

14. Check the continuity of the function f given below at 1 and 2.
AP Inter 1st Year Maths 1B Model Paper Set 1 with Solutions 1

15. If f(x) = log x (x > 0), then show that f'(x) = \(\frac{1}{x}\) by first principle.

16. A particle is moving along a line according to S = f(t) = 4t3 – 3t2 + 5t – 1 where S is measured in meters and t is measured in seconds. Find the velocity and acceleration at time t. At what time the acceleration is zero.

17. Find the value of K so that the length of the subnormal at any point on the curve xyk = ak+1 is a constant.

Section – C

III. Long Answer Questions.

  1. Answer any Five Questions.
  2. Each Question carries Seven marks.

18. The base of an equilateral triangle is x + y – 2 = 0 and the opposite vertex is (2, – 1). Find the equation of the remaining axes.

19. Show that the product of the perpendicular distances from the origin to the pair of straight lines represented ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 is \(\frac{|c|}{\sqrt{(a-b)^2+4 h^2}}\).

20. Prove that the lines represented by the equations x2 – 4xy + y2 = 0 and x + y = 3 form an equiteral triangle.

AP Inter 1st Year Maths 1B Model Paper Set 1 with Solutions

21. If a variable line in two adjacent positions has direction cosines (l, m, n) and (l + δl, m + δm, n + δn), show that the small angle δθ between two positions. Is given by (δθ)2 = (δl)2 + (δm)2 + (δn)2.

22. If y = xtan x + (sin x)cos x, find \(\frac{d y}{d x}\).

23. Show that the tangent at the point P(2, -2) on the curve y (1 – x) = x makes intercepts of equal length on the co-ordinate axes and the normal at P passes through the origin.

24. The volume of a cube is increasing at a rate of 9 cubic centimeters per second. How fast is the surface area increasing when the length of the edge is 10 centimeters ?

Leave a Comment