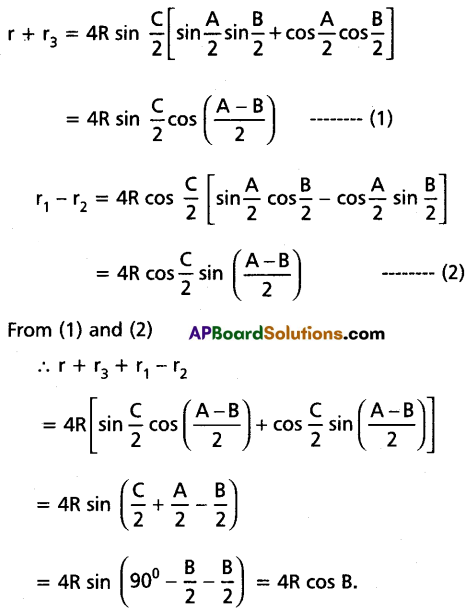AP Inter 1st Year Maths 1A Question Paper May 2018

Thoroughly analyzing AP Inter 1st Year Maths 1A Model Papers and AP Inter 1st Year Maths 1A Question Paper May 2018 helps students identify their strengths and weaknesses.

AP Inter 1st Year Maths 1A Question Paper May 2018

Time: 3 Hours
Maximum Marks: 75

Note: This Question Paper consists of three sections A, B, and C.

Section – A
(10 × 2 = 20 Marks)

I. Very Short Answer Type Questions.

• Answer All the questions.
• Each Question carries Two marks.

Question 1.
If f: R – {±1} → R is defined by f(x) = \(\log \left|\frac{1+x}{1-x}\right|\), then show that \(f\left(\frac{2 x}{1+x^2}\right)\) = 2f(x).
Solution:

Question 2.
Find the domain of the real-valued function \(\sqrt{x^2-25}\).
Solution:
Given f(x) = \(\sqrt{x^2-25}\)
x² – 25 ≥ 0
⇒ (x + 5) (x – 5) ≥ 0
⇒ x ∈ (-∞, -5] ∪ [5, ∞)
∴ Domain of f = (-∞, -5] ∪ [5, ∞)

Question 3.
If A = \(\left[\begin{array}{cc}
2 & -4 \\
-5 & 3
\end{array}\right]\) then find A + A^T and AA^T.
Solution:

Question 4.
Find the rank of the matrix \(\left[\begin{array}{lll}
1 & 1 & 1 \\
1 & 1 & 1 \\
1 & 1 & 1
\end{array}\right]\).
Solution:
Let A = \(\left[\begin{array}{lll}
1 & 1 & 1 \\
1 & 1 & 1 \\
1 & 1 & 1
\end{array}\right]\)
|A| = \(\left|\begin{array}{lll}
1 & 1 & 1 \\
1 & 1 & 1 \\
1 & 1 & 1
\end{array}\right|\) = 0
∴ Rank of (A) ≠ 3
All the 2 × 2 minors of A is zero.
∴ Rank of (A) ≠ 2
Since A is a non-zero matrix.
∴ Rank of (A) = 1

Question 5.
Let \(\bar{a}=\bar{i}+2 \bar{j}+3 \bar{k}\) and \(\overline{\mathrm{b}}=3 \overline{\mathrm{i}}+\overline{\mathrm{j}}\). Find the unit vector in the direction of \(\bar{a}+\bar{b}\).
Solution:

Question 6.
Find the vector equation of the plane passing through the points (0, 0, 0), (0, 5, 0) and (2, 0, 1).
Solution:

Question 7.
If \(\overline{\mathrm{a}}=\overline{\mathrm{i}}+2 \overline{\mathrm{j}}-3 \overline{\mathrm{k}}\) and \(\bar{b}=3 \bar{i}-\bar{j}+2 \bar{k}\), then show that \(\bar{a}+\bar{b}\) and \(\bar{a}-\bar{b}\) are perpendicular to each other.
Solution:

Question 8.
If sec θ + tan θ = \(\frac{2}{3}\), find the value of sin θ.
Solution:
Given sec θ + tan θ = \(\frac{2}{3}\)

Question 9.
If A is not an integral multiple of \(\frac{\pi}{2}\), prove that tan A + cot A = 2 cosec 2A.
Solution:

Question 10.
If cosh x = \(\frac{5}{2}\), find the values of (i) cosh (2x) and (ii) sinh (2x).
Solution:
Given cosh x = \(\frac{5}{2}\)
We know cosh²x – sinh²x = 1
⇒ sinh²x = cosh²x – 1
= \(\frac{25}{4}\) – 1

Section – B
(5 × 4 = 20 Marks)

II. Short Answer Type Questions.

• Answer any Five questions.
• Each question carries Four marks.

Question 11.
If θ – φ = \(\frac{\pi}{2}\), then show that \(\left[\begin{array}{cc}
\cos ^2 \theta & \cos \theta \sin \theta \\
\cos \theta \sin \theta & \sin ^2 \theta
\end{array}\right]\left[\begin{array}{cc}
\cos ^2 \phi & \cos \theta \sin \phi \\
\cos \phi \sin \phi & \sin ^2 \phi
\end{array}\right]\) = 0.
Solution:
Given θ – φ = \(\frac{\pi}{2}\)

Question 12.
Let ABCDEF be a regular hexagon with a center ‘O’. Then show that \(\overline{\mathrm{AB}}+\overline{\mathrm{AC}}+\overline{\mathrm{AD}}+\overline{\mathrm{AE}}+\overline{\mathrm{AF}}=3 \overline{\mathrm{AD}}=6 \overline{\mathrm{AO}}\).
Solution:

Question 13.
Let \(\overline{\mathrm{a}}=4 \overline{\mathrm{i}}+5 \overline{\mathrm{j}}-\overline{\mathrm{k}}, \overline{\mathrm{b}}=\overline{\mathrm{i}}-4 \overline{\mathrm{j}}+5 \overline{\mathrm{k}}\) and \(\overline{\mathrm{c}}=3 \overline{\mathrm{i}}+\overline{\mathrm{j}}-\overline{\mathrm{k}}\). Find vector \(\bar{\alpha}\) which is perpendicular to both \(\bar{a}\) and \(\bar{b}\) and \(\bar{\alpha} \cdot \bar{c}\) = 21.
Solution:

Question 14.
Prove that cos² 76° + cos² 16° – cos 76° cos 16° = \(\frac{3}{4}\).
Solution:
L.H.S = cos² 76° + cos² 16° – cos 76° cos 16°
= cos² 76° + 1 – sin² 16° – \(\frac{1}{2}\)(2 cos 76° cos 16°)
= 1 + cos² 76°- sin² 16° – \(\frac{1}{2}\)[cos(76° + 16°) + cos(76° – 16°)]
= 1 + cos(76° + 16°) cos(76° – 16°) – \(\frac{1}{2}\)[cos 92° – cos 60°]
= 1 + cos 92° . \(\frac{1}{2}\) – \(\frac{1}{2}\) cos 92° – \(\frac{1}{2}\) . \(\frac{1}{2}\)
= 1 – \(\frac{1}{4}\)
= \(\frac{3}{4}\)
= R.H.S
∴ L.H.S = R.H.S
∴ cos² 76° + cos² 16° – cos 76° cos 16° = \(\frac{3}{4}\)

Question 15.
Solve √2(sin x + cos x) = √3.
Solution:
Given that √2 (sin x + cos x) = √3
⇒ sin x + cos x = \(\frac{\sqrt{3}}{\sqrt{2}}\)
By dividing both sides by √2, we get
⇒ cos x . \(\frac{1}{\sqrt{2}}\) + sin x . \(\frac{1}{\sqrt{2}}\) = \(\frac{\sqrt{3}}{\sqrt{2}} \cdot \frac{1}{\sqrt{2}}\)
⇒ cos x cos 45° + sin x sin 45° = \(\frac{\sqrt{3}}{2}\)
⇒ cos (x – 45°) = \(\frac{\sqrt{3}}{2}\)
The principal value of cos(x – 45°) = \(\frac{\sqrt{3}}{2}\) is 30°
∴ x – 45° = 2nπ ≠ 30°, n ∈ Z
x – 45° = 2nπ + 30° (or) x – 45° = 2nπ – 30°, n ∈ Z
⇒ x = 2nπ + 75° (or) x = 2nπ + 15°, n ∈ Z
⇒ x = 2nπ + \(\frac{5 \pi}{12}\) (or) x = 2nπ + \(\frac{\pi}{12}\), n ∈ Z
∴ Solution set X = [2nπ + \(\frac{5 \pi}{12}\) / n ∈ Z] ∪ [2nπ + \(\frac{\pi}{12}\) / n ∈ Z]

Question 16.
Prove that \(\cos \left(2 \tan ^{-1} \frac{1}{7}\right)=\sin \left(2 \tan ^{-1} \frac{3}{4}\right)\).
Solution:

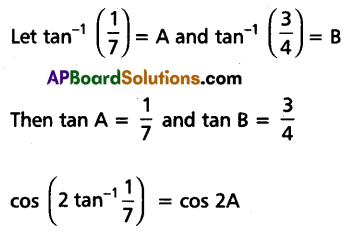
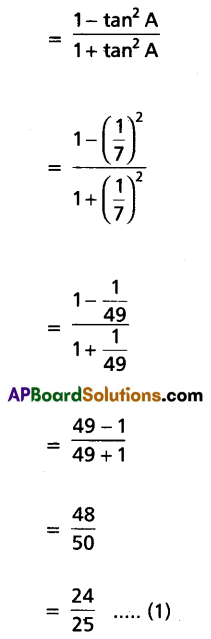
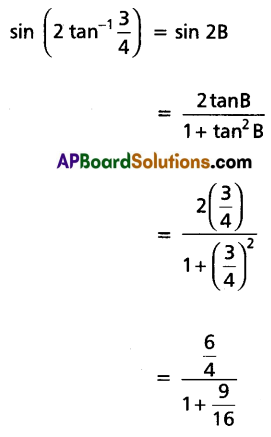
Question 17.
Show that a² cot A + b² cot B + c² cot C = \(\frac{abc}{R}\) in a triangle.
Solution:
L.H.S = a² cot A + b² cot B + c² cot C
= \(4 R^2 \sin ^2 A \cdot \frac{\cos A}{\sin A}+4 R^2 \sin ^2 B \cdot \frac{\cos B}{\sin B}+4 R^2 \sin ^2 C \cdot \frac{\cos C}{\sin C}\)
= 2R² (2 sin A cos A + 2 sin B cos B + 2 sin C cos C)
= 2R² (sin 2A + sin 2B + sin 2C)
= 2R² (4 sin A sin B sin C)
Since sin 2A + sin 2B + sin 2C = 4 sin A sin B sin C
= \(\frac{1}{R}\) (2R sin A) (2R sin B) (2R sin C)
= \(\frac{1}{R}\) a.b.c
= \(\frac{abc}{R}\)
= R.H.S.
Hence a² cot A + b² cot B + c² cot C = \(\frac{abc}{R}\)

Section – C
(5 × 7 = 35 Marks)

III. Long Answer Type Questions.

• Answer any Five questions.
• Each question carries Seven marks.

Question 18.
Let f: A → B be a function. Then f is a bijection if and only if there exists a function g: B → A such that fog = I_B and gof = I_A and, in this case, g = f^-1.
Solution:
To show that g = f^-1
first, we have to show that f^-1 exists,
i.e., we have to show that f is a bijection.
(i) To prove f is one-one.
Let x, y ∈ A and f(x) = f(y)
⇒ g[f(x)l = g[f(y)]
⇒ (gof) (x) = (gof) (y)
⇒ I_A (x) = I_A (y)
⇒ x = y
∴ f is one-one.
(ii) To prove f is onto
Let b ∈ B
Since g: B → A
⇒ g(b) ∈ A
let g(b) = a Then f(a) = f[g(b)]
= (fog) (b)
= I_B (b)
= b
∴ f is onto
∴ f is one-one and onto
∴ f is a bijection
∴ f^-1 exists.
(iii) To prove g = f^-1
f:A → B ⇒ f^-1: B → A
∴ g and f^-1 have the same domain B.
Let b ∈ B, since f^-1: B → A
⇒ f^-1(b) ∈ A
Let f^-1(b) = a then f(a) = b
g(b) = g[f(a)] = (gof) (a) = I_A (a) = a = f^-1(b)
Hence g = f^-1

Question 19.
Using mathematical induction, prove that \(3.5^{2 n+1}+2^{3 n+1}\) is divisible by 17, for all n ∈ N.
Solution:
Let p(n) be the statement that \(3.5^{2 n+1}+2^{3 n+1}\) is divisible by 17.
If n = 1 then
\(3.5^{2+1}+2^{3+1}\) = 3 . 5³ + 2⁴
= 375 + 16
= 391
= 17(23)
∴ p(1) is true
Assume that p(k) is true.

∴ p(k + 1) is true.
∴ By the principle of finite mathematical induction p(n) is true for all n ∈ N.
Hence \(3.5^{2 n+1}+2^{3 n+1}\) is divisible by 17 for all n ∈ N.

Question 20.
Show that \({det}\left[\begin{array}{ccc}
a-b-c & 2 a & 2 a \\
2 b & b-c-a & 2 b \\
2 c & 2 c & c-a-b
\end{array}\right]\) = (a + b + c)³.
Solution:

= (a + b + c) (-a – b – c) (-a – b – c)
= (a + b + c) (-1) (a + b + c) (-1) (a + b + c)
= (a + b + c)³
= R.H.S
∴ L.H.S = R.H.S
∴ \({det}\left[\begin{array}{ccc}
a-b-c & 2 a & 2 a \\
2 b & b-c-a & 2 b \\
2 c & 2 c & c-a-b
\end{array}\right]\) = (a + b + c)³

Question 21.
Solve the following equations by Gauss-Jordan Method:
x + y + z = 1, 2x + 2y + 3z = 6 and x + 4y + 9z = 3.
Solution:
Given x + y + z = 1
2x + 2y + 3z = 6
x + 4y + 9z = 3
The given system of equations can be expressed as AX = B


∴ x = 7, y = -10, z = 4

Question 22.
If \(\bar{a}=\bar{i}-2 \bar{j}-3 \bar{k}, \bar{b}=2 \bar{i}+\bar{j}-\bar{k}\) and \(\bar{c}=\bar{i}+3 \bar{j}-2 \bar{k}\), verify that \(\overline{\mathrm{a}} \times(\overline{\mathrm{b}} \times \overline{\mathrm{c}}) \neq(\overline{\mathrm{a}} \times \overline{\mathrm{b}}) \times \overline{\mathrm{c}}\).
Solution:

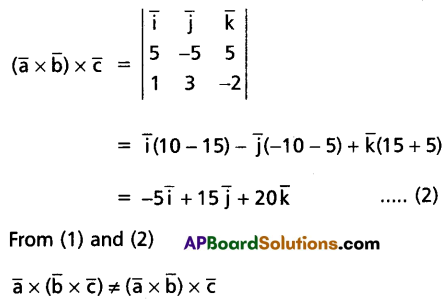
Question 23.
If A, B, C are the angles in a triangle, then prove that \(\sin ^2 \frac{A}{2}+\sin ^2 \frac{B}{2}-\sin ^2 \frac{C}{2}=1-2 \cos \frac{A}{2} \cos \frac{B}{2} \sin \frac{C}{2}\).
Solution:
Given A, B, C are the angles of a triangle.
∴ A + B + C = 180°
⇒ \(\frac{A}{2}+\frac{B}{2}+\frac{C}{2}\) = 90°

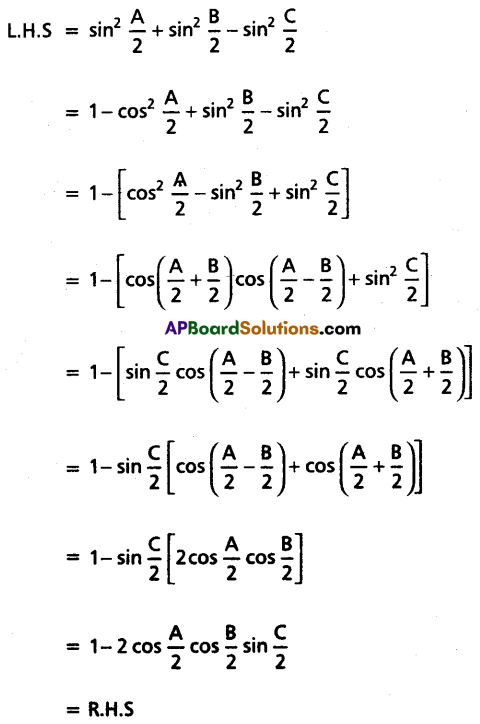
∴ \(\sin ^2 \frac{A}{2}+\sin ^2 \frac{B}{2}-\sin ^2 \frac{C}{2}=1-2 \cos \frac{A}{2} \cos \frac{B}{2} \sin \frac{C}{2}\)

Question 24.
Show that r + r₃ + r₁ – r₂ = 4R cos B, in ΔABC.
Solution: