AP Inter 1st Year Maths 1A Question Paper March 2018

Thoroughly analyzing AP Inter 1st Year Maths 1A Model Papers and AP Inter 1st Year Maths 1A Question Paper March 2018 helps students identify their strengths and weaknesses.

AP Inter 1st Year Maths 1A Question Paper March 2018

Time: 3 Hours
Maximum Marks: 75

Note: This question paper consists of three sections A, B, and C.

Section – A
(10 × 2 = 20 Marks)

I. Very Short Answer Type Questions.

• Answer all the questions.
• Each question carries two marks.

Question 1.
Find the domain of the real-valued function f(x) = \(\sqrt{x^2-25}\).
Solution:
Given f(x) = \(\sqrt{x^2-25}\)
f(x) ∈ R ⇔ x² – 25 ≥ 0
⇔ (x + 5) (x – 5) ≥ 0
⇔ x ∈ (-∞, -5) ∪ (5, ∞)
∴ Domain of f = (-∞, -5) ∪ (5, ∞).

Question 2.
If f : R → R, g : R → R are defined by f(x) = 3x – 1, g(x) = x² + 1 then find (fog) (2).
Solution:
Given f(x) = 3x – 1 and g(x) = x² + 1
(fog) (2) = f[g(2)]
= f[2² + 1]
= f[4 + 1]
= f(5)
= 3(5) – 1
= 15 – 1
= 14
∴ (fog) (2) = 14

Question 3.
Define a symmetric matrix. Give one example of order 3 × 3.
Solution:
Symmetric Matrix: A square matrix ‘A’ is said to be a symmetric matrix if A^T = A.
Example: A = \(\left[\begin{array}{ccc}
1 & 2 & 0 \\
2 & -3 & -1 \\
0 & -1 & 4
\end{array}\right]\)

Question 4.
Find the inverse of the matrix \(\left[\begin{array}{cc}
1 & 2 \\
3 & -5
\end{array}\right]\).
Solution:

Question 5.
If the vectors \(-3 \bar{i}+4 \bar{j}+\lambda \bar{k}\) and \(\mu \bar{i}+8 \overline{\mathrm{j}}+6 \overline{\mathrm{k}}\) are collinear then find λ and μ.
Solution:

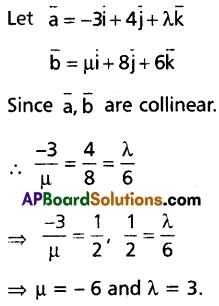
Question 6.
Find the vector equation of the plane passing through the points (0, 0, 0), (0, 5, 0) and (2, 0, 1).
Solution:
Let A = (0, 0, 0)
B = (0, 5, 0)
C = (2, 0, 1)
The vector equation of the plane passing through the points A(\(\bar{a}\)), B(\(\bar{b}\)), C(\(\bar{c}\)) is

Question 7.
Find the angle between the vectors \(\bar{i}+2 \bar{j}+3 \bar{k}\) and \(3 \bar{i}-\bar{j}+2 \bar{k}\).
Solution:

Question 8.
Find the value of sin 330° cos 120° + cos 210° sin 300°.
Solution:
sin 330° . cos 120° + cos 210° . sin 300°
= sin (360° – 30°) . cos (180° – 60°) + cos(180° + 30°) . sin(360° – 60°)
= (-sin 30°) . (-cos 60°) + (-cos 30°) . (-sin 60°)
= \(\left(\frac{-1}{2}\right)\left(\frac{-1}{2}\right)+\left(\frac{-\sqrt{3}}{2}\right)\left(\frac{-\sqrt{3}}{2}\right)\)
= \(\frac{1}{4}+\frac{3}{4}\)
= 1
∴ sin 330° . cos 120° + cos 210° . sin 300° = 1

Question 9.
Find the extreme values of cos 2x + cos²x.
Solution:
Let f(x) = cos 2x + cos²x
= cos 2x + \(\frac{1+\cos 2 x}{2}\)
= cos 2x + \(\frac{1}{2}\) + \(\frac{1}{2}\) cos 2x
= \(\frac{1}{2}\) + (1 + \(\frac{1}{2}\)) cos 2x
= \(\frac{1}{2}\) + \(\frac{3}{2}\) cos 2x
We know -1 ≤ cos 2x ≤ 1
⇒ \(\frac{-3}{2} \leq \frac{3}{2} \cos 2 x \leq \frac{3}{2}\)
⇒ \(\frac{1}{2}-\frac{3}{2} \leq \frac{1}{2}+\frac{3}{2} \cos 2 x \leq \frac{1}{2}+\frac{3}{2}\)
⇒ -1 ≤ f(x) ≤ 2
∴ Minimum value = -1, Maximum value = 2

Question 10.
For any x ∈ R show that cosh 2x = 2 cosh²x – 1.
Solution:
L.H.S = cosh 2x
= cosh²x + sinh²x
= cosh²x + cosh²x – 1 {∵ cosh²x – sinh²x = 1}
= 2 cosh²x – 1
= R.H.S
∴ L.H.S = R.H.S
Hence cosh 2x = 2 cosh²x – 1

Section – B
(5 × 4 = 20 Marks)

II. Short Answer Type Questions.

• Answer any five questions.
• Each question carries four marks.

Question 11.
If A = \(\left[\begin{array}{rr}
7 & -2 \\
-1 & 2 \\
5 & 3
\end{array}\right]\) and B = \(\left[\begin{array}{rr}
-2 & -1 \\
4 & 2 \\
-1 & 0
\end{array}\right]\) then find AB’ and BA’.
Solution:

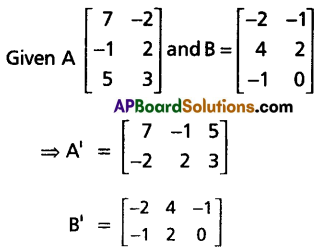
Question 12.
If \(\bar{a}, \bar{b}, \bar{c}\) are non-coplanar vectors, prove that the following four points are co-planar.
\(-\overline{\mathrm{a}}+4 \overline{\mathrm{b}}-3 \overline{\mathrm{c}}, 3 \overline{\mathrm{a}},+2 \overline{\mathrm{b}}-5 \overline{\mathrm{c}},-3 \overline{\mathrm{a}}+8 \overline{\mathrm{b}}-5 \overline{\mathrm{c}} \text { and }-3 \overline{\mathrm{a}}+2 \overline{\mathrm{b}}+\overline{\mathrm{c}}\)
Solution:

Question 13.
Let \(\bar{a}\) and \(\bar{b}\) be vectors, satisfying |\(\bar{a}\)| = |\(\bar{b}\)| = 5 and (\(\bar{a}\), \(\bar{b}\)) = 45°. Find the area of the triangle having \(\bar{a}-2 \bar{b}\) and \(3 \bar{a}+2 \bar{b}\) as two of its sides.
Solution:
Given |\(\bar{a}\)| = |\(\bar{b}\)| = 5 and (\(\bar{a}\), \(\bar{b}\)) = 45°
Let \(\overline{\mathrm{AB}}=\overline{\mathrm{a}}-2 \overline{\mathrm{b}}\)

Question 14.
If A is not an integral multiple of \(\frac{\pi}{2}\) then prove that
(i) tan A + cot A = 2 cosec 2A
(ii) cot A – tan A = 2 cot 2A
Solution:

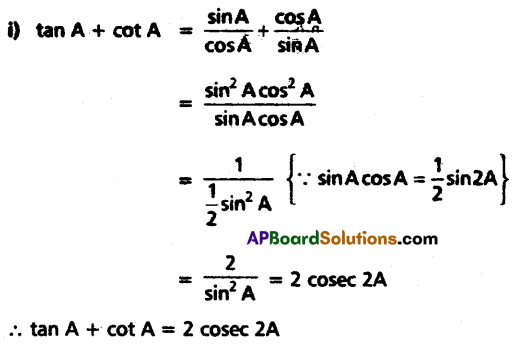
Question 15.
Solve the equation √3 sin θ – cos θ = √2.
Solution:

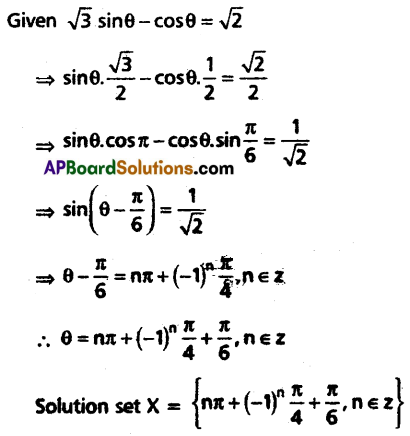
Question 16.
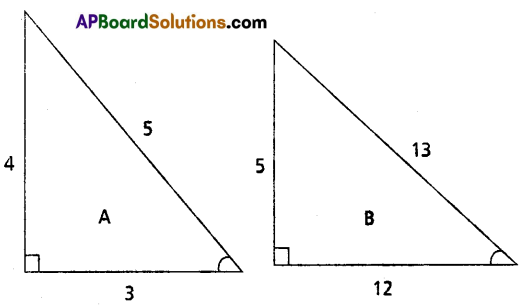
Prove that \(\sin ^{-1}\left(\frac{4}{5}\right)+\sin ^{-1}\left(\frac{5}{13}\right)+\sin ^{-1}\left(\frac{16}{65}\right)=\frac{\pi}{2}\).
Solution:
Let \(\sin ^{-1}\left(\frac{4}{5}\right)\) = A and \(\sin ^{-1}\left(\frac{5}{13}\right)\) = B
Then sin A = \(\frac{4}{5}\) and sin B = \(\frac{5}{13}\)

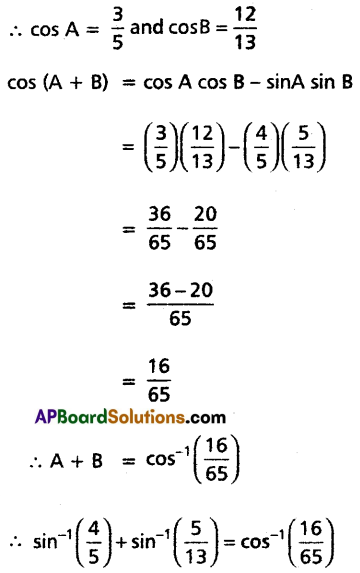
Question 17.
If a = (b – c) sec θ, prove that tan θ = \(\frac{2 \sqrt{b c}}{b-c} \sin \frac{A}{2}\).
Solution:
Given a = (b – c) sec θ
⇒ sec θ = \(\frac{a}{b-c}\)
We know tan2θ = sec²θ – 1

Section – C
(5 × 7 = 35 Marks)

III. Long Answer Type Questions.

• Attempt any five questions.
• Each question carries seven marks.

Question 18.
Let f: A → B, g: B → C be bijections then prove that gof: A → C is a bijection.
Solution:
Given f: A → B, g: B → C be bijections.
(i) To prove gof: A → C, is one-one
Let a₁, a₂ ∈ a Then f(a₁), f(a₂) ∈ B
(gof)(a₁) = (gof)(a₂)
⇒ g[f(a₁)] = g[f(a₂)]
⇒ f(a₁) = f(a₂) {∵ g is one-one}
⇒ a₁ = a₂ {∵ f is one-one}
∴ gof: A → C is one-one

(ii) To prove gof: A → C is onto
Let c ∈ c
Since g: B → C is onto
∴ There exists b ∈ B such that g(b) = c
Since f: A → B is onto
∴ There exists a ∈ A such that f(a) = b
c = g(b) = g[f(a)] = (gof) (a)
∴ There exists a ∈ A such that (gof) (a) = c
∴ gof: A → C is onto
Hence gof: A → C is a bijective function.

Question 19.
Using mathematical induction, prove that \(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+\ldots .+\frac{1}{(2 n-1)(2 n+1)}=\frac{n}{2 n+1}\) for all n ∈ N.
Solution:
Let p(n) be the statement that


∴ p(k + 1) is true.
∴ By the principle of finite mathematical induction p(n) is true for all n ∈ N.
∴ \(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+\ldots .+\frac{1}{(2 n-1)(2 n+1)}=\frac{n}{2 n+1}\) for all n ∈ N.

Question 20.
Show that \(\left|\begin{array}{ccc}
a+b+2 c & a & b \\
c & b+c+2 a & b \\
c & a & c+a+2 b
\end{array}\right|\) = 2(a + b + c)³.
Solution:

= 2(a + b + c) (1) (b + c + a) (c + a + b)
= 2(a + b + c)³
= R.H.S.
∴ L.H.S = R.H.S
Hence \(\left|\begin{array}{ccc}
a+b+2 c & a & b \\
c & b+c+2 a & b \\
c & a & c+a+2 b
\end{array}\right|\) = 2(a + b + c)³

Question 21.
Solve the following system of equations by Gauss-Jordan Method:
2x – y + 3z = 9, x + y + z = 6 and x – y + z = 2
Solution:
Given that the system of equations are
2x – y + 3z = 9
x + y + z = 6
x – y + z = 2
The given system of equations can be expressed as AX = B


∴ x = 1, y = 2, z = 3

Question 22.
For any four vectors \(\bar{a}, \bar{b}, \bar{c}\) and \(\bar{d}\), prove that
(i) \((\overline{\mathrm{a}} \times \overline{\mathrm{b}}) \times(\overline{\mathrm{c}} \times \overline{\mathrm{d}})=[\overline{\mathrm{a}} \overline{\mathrm{c}} \overline{\mathrm{d}}] \overline{\mathrm{b}}-[\overline{\mathrm{b}} \overline{\mathrm{c}} \overline{\mathrm{d}}] \overline{\mathrm{a}}\)
(ii) \((\overline{\mathrm{a}} \times \overline{\mathrm{b}}) \times(\overline{\mathrm{c}} \times \overline{\mathrm{d}})=[\overline{\mathrm{a}} \overline{\mathrm{b}} \overline{\mathrm{d}}] \overline{\mathrm{c}}-[\overline{\mathrm{a}} \overline{\mathrm{b}} \overline{\mathrm{c}}] \overline{\mathrm{d}}\)
Solution:

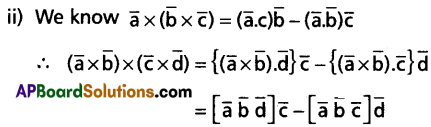
Question 23.
If A, B, C are the angles in a triangle, then prove that cos A + cos B + cos C = 1 + 4\(\sin \left(\frac{A}{2}\right) \sin \left(\frac{B}{2}\right) \sin \left(\frac{C}{2}\right)\).
Solution:
Since A, B, C are the angles of a triangle.
∴ A + B + C = 180°
⇒ \(\frac{A}{2}+\frac{B}{2}+\frac{C}{2}\) = 90°
L.H.S. = cos A + cos B + cos C

∴ L.H.S = R.H.S
Hence cos A + cos B + cos C = 1 + 4\(\sin \left(\frac{A}{2}\right) \sin \left(\frac{B}{2}\right) \sin \left(\frac{C}{2}\right)\)

Question 24.
Show that in any triangle ABC, r + r₃ + r₁ – r₂ = 4R cos B.
Solution: