TS Inter 2nd Year Physics Question Paper May 2018

Thoroughly analyzing TS Inter 2nd Year Physics Model Papers and TS Inter 2nd Year Physics Question Paper May 2018 helps students identify their strengths and weaknesses.

TS Inter 2nd Year Physics Question Paper May 2018

Time: 3 Hours
Maximum Marks: 60

Section – A (10 × 2 = 20)

Note :

• Answer ALL questions.
• Each question carries TWO marks.
• ALL are very short answer type questions.

Question 1.
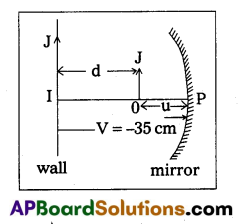
A concave mirror of focal length 10 cm is placed at a dis-tance 35 cm from a wall. How far from the wall should an object be placed so that its real image is formed on the wall ?
Answer:
Given f = -10 cm (concave)
V = -35 cm; d = ?
using \(\frac{1}{\mathrm{u}}\) + \(\frac{1}{\mathrm{v}}\) = \(\frac{1}{\mathrm{f}}\)
\(\frac{1}{\mathrm{u}}\) – \(\frac{1}{35}\) = \(\frac{-1}{10}\)
\(\frac{1}{\mathrm{u}}\) = \(\frac{1}{35}\) = – \(\frac{1}{10}\) = \(\frac{-25}{35 \times 10}\)
∴ u = -14 cm.
∴ Distance between wall and object, d = 35 – 14 = 21 cm.

Question 2.
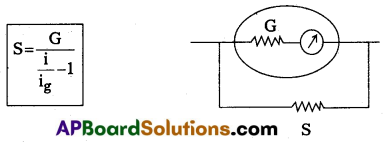
How do you convert a moving coll galvanometer into an ammeter?
Answer:
A small resistance is connected in parallel to the moving coil galvanometer, then it converts to Ammeter.

Question 3.
Magnetic lines form continuous closed loops. Why?
Answer:
Magnetic lines of force always start from north pole and forming curved path, enter south pole and travel to north pole inside the magnet. Thus lines of force are forming closed loops.

Question 4.
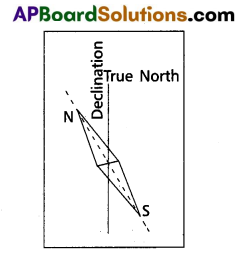
Define Magnetic declination.
Answer:
Magnetic Declination (D) : The angle between the true geographic north and the north shown by a compass needle is called magnetic declination or simply declination (D).

Question 5.
What is transformer ratio ?
Answer:
The ratio of secondary e.m.f to the primary e.m.f (or) num¬ber of turns in secondary to the number of turns in the primary is called the transformer ratio.
Transformer ratio = \(\frac{\mathrm{V}_{\mathrm{S}}}{\mathrm{V}_{\mathrm{P}}}\) = \(\frac{\mathrm{N}_{\mathrm{S}}}{\mathrm{N}_{\mathrm{P}}}\)

Question 6.
If the wavelength of electromagnetic radiation is doubled, what happens to the energy of photon ?
Answer:
Photon energy (E) = hv = \(\frac{\mathrm{hc}}{\lambda}\)
E ∝ \(\frac{1}{\lambda}\)
Given
λ₁ = 1,
λ₂ = 2λ,
E₁ = E
\(\frac{E_1}{E_2}=\frac{\lambda_2}{\lambda_1}\)
\(\frac{E}{E_2}=\frac{2 \lambda}{\lambda}\)
E₂ = \(\frac{E}{2}\)
∴ The energy of photon reduces to half of its initial value.

Question 7.
Write down Einstein’s photoelectric equation.
Answer:
K_max = \(\frac{1}{2}\) m V²_max = hυ – Φ₀

Question 8.
State Heisenberg’s uncertainty principle.
Answer:
Uncertainty principle states that “it is impossible to measure both position (Δx) and momentum of an electron (Δp) [or any other particle] at the same time exactly”, i.e., Δx, Δp ≈ h where Δx is uncertainty in the specificatipn of position and Δp is uncertainty in the specification of momentum.

Question 9.
What is a p-type semiconductor ? What are the majority charge carriers in it ?
Answer:
If a trivalent impurity is added to a tetravalent semiconductor, it is called p-type semi-conductor.
In p-type semiconductor majority charge carriers are holes and minority charge carriers are electrons.

Question 10.
Define modulation. Why is it necessary ?
Answer:
Modulation: The process of combining low frequency audio signal with high frequency carrier wave is called modulation.

The audio frequency signals cannot be transmitted over long distances faithfully. Therefore they are combined with high frequency waves and transmitted.

Section – B (6 × 4 = 24)

Note :

• Answer ANY SIX of the following questions,
• Each question carries FOUR marks.
• ALL are short answer type questions.

Question 11.
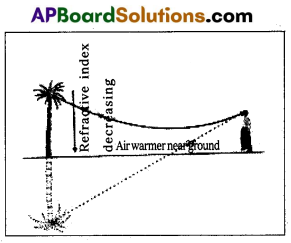
Explain the formation of a mirage.
Answer:
In a desert, the sand becomes very hot during the day time and it rapidly heats the layer of air which is in its contact. So density of air decreases. As a result the successive upward layers are denser than lower layers.

When a beam of light travelling from the top of a tree enters a rarer layer, it is refracted away from the normal. As a result at the surface of layers of air, each time the angle of incidence increases and ultimately a stage is reached, when the angle of incidence becomes greater than the critical angle between the two layers, the incident ray suffers total internal reflection.

So it appears as inverted image of the tree is formed and the same looks like a pool of water to the observer.

Question 12.
Derive the expression for the intensity at a point where in-terference of light occurs. Arrive at the conditions for maximum and zero intensity.
Answer:
Let y₁ and y₂ be the displacements of the two waves having same amplitude a and Φ is the phase difference between them.
y₁ = a sin ωt …………. (1)
y₂ = a sin (ωt + Φ) ……….. (2)
The resultant displacement y = y₁ + y₂
y = a sin ωt + a sin (ωt + Φ)
y = a sin ωt + a sin ωt cos Φ + a cos ωt sin Φ
y = a sin ωt [1 + cos Φ] + cos ωt (a sin Φ) …………. (3)
Let R cos θ = a(l + cos Φ) …………. (4)

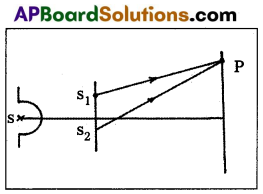
R sin θ = a sin Φ …………. (5)
y = R sin ωt. cos θ + R cos ωt. sin θ
y = R sin (ωt + θ) …………. (6)
Where R is the resultant amplitude at P squaring equations (4) and (5), then adding
R² [cos² θ + sin² θ] = a² [1 + cos² Φ + 2 cos Φ + sin² Φ]
R² [1] = a² [1 + 1 + 2 cos Φ]
I = R² = 2a² [1 + cos Φ] = 2a² × 2 cos²\(\frac{\phi}{2}\); I = 4a² cos² \(\frac{\phi}{2}\) ……………. (7)

i) Maximum intensity (I_max)
cos² \(\frac{\phi}{2}\) = 1
Φ = 2nπ
where n = 0, 1, 2, 3 …………….
Φ = 0, 2π, 4π, 6π ………….
∴ I_max = 4a².

ii) Minimum intensity (I_min)
cos² \(\frac{\phi}{2}\) = 0
Φ = (2n + 1)π
where n = 0, 1, 2, 3 …………….
Φ = π, 3π, 5π, 7π ………….
I_min = 0.

Question 13.
Derive the equation for the moment of couple acting on an electric dipole in a uniform electric field.
Answer:

• A pair of opposite charges separated by a small distance is called dipole.
• Consider the charge of dipole are -q and +q coulomb and the distance between them is 2a.
• Then the electric dipole moment P is given by P = q × 2a = 2aq. It is a vector. It’s direction is from -q to +q along the axis of dipole.
• It is placed in a uniform electric field E, making an angle 0 with field direction as shown in fig.
• Due to electric field force on +q is F = +qE and force on -q is F = -qE.
• These two equal and opposite charges constitute torque or moment of couple.
  i.e., torque, τ = ⊥^r distance × magnitude of one of force
  ∴ τ = (2a sin θ) qE = 2aqE sin θ = PE sin θ
  In vector form, \(\vec{\tau}=\overrightarrow{\mathrm{P}} \times \overrightarrow{\mathrm{E}}\)

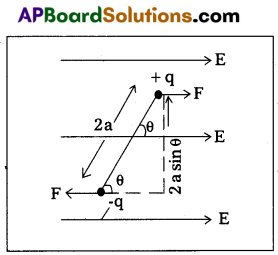
Question 14.
Derive an expression for the capacitance of a parallel plate capacitor.
Answer:
Consider two parallel plates A and B separated by a distance d in air. The upper plate A is given a charge +q and a lower plate B given a charge -q.
By using Gauss law, first we calculate the value of elec- trie field E.

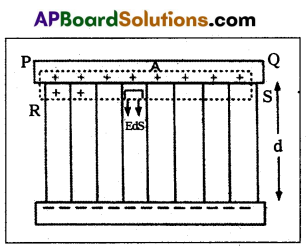
Consider a Gaussian surface PQRS. The flux through the ends PR and QS is zero, (∵ angle between E and ds is 90°). Electric flux through the surface PQ is zero, because inside the conductor charge is zero.
The only contribution of electric flux is due to the surface RS. Total electric flux through the entire Gaussian surface is
Φ_E = \(\oint \mathrm{E} \cdot \mathrm{dS}=\oint \mathrm{EdS} \cos \theta\)
(∵ Angle between E and dS is zero, i.e., θ = 0)
Φ_E = \(\oint \mathrm{E} \cdot \mathrm{dS}\) (∵ \(\oint \mathrm{dS}=\mathrm{A}\))
Let A be the area of each plate Φ_E = E.A …………. (1)
Applying Gauss law Φ_E = \(\frac{1}{\varepsilon_0}\) q ………… (2)
From eq’s (1) and (2), EA = \(\frac{\mathrm{q}}{\varepsilon_0}\)
E = \(\frac{\mathrm{q}}{\varepsilon_0 \mathrm{~A}}\) …………. (3)
The potential difference V between the plates can be written as
V = E.d = \(\frac{\mathrm{q}}{\varepsilon_0 \mathrm{~A}}\).d (∵ C = \(\frac{\mathrm{q}}{\mathrm{v}}\))
\(\frac{\mathrm{q}}{\mathrm{v}}\) = \(\frac{\varepsilon_0 \mathrm{~A}}{\mathrm{~d}}\)
∴ C = \(\frac{\varepsilon_0 \mathrm{~A}}{\mathrm{~d}}\)

Question 15.
A circular coil of wire consisting of 100 turns, each of radius 8.0 cm cames a current of 0.40 A. What is the magnitude of the magnetic field B at the centre of the coil ?
Solution:
Given, n = 100; r = 8 cm = 8 × 10^-2m; i = 0.40 A
The magnetic field B at the centre of coil, B = \(\frac{\mu_0 \mathrm{ni}}{2 \mathrm{r}}\)
⇒ B = \(\frac{4 \pi \times 10^{-7} \times 100 \times 0.4}{2 \times 8 \times 10^{-2}}\)
= \(\frac{4 \times 3.14 \times 4 \times 10^{-6}}{16 \times 10^{-2}}\)
∴ B = 3.14 × 10^-4T.

Question 16.
Apair of adjacent coils has a mutual inductance of 1.5 H. If the current in one coil changes from 0 to 20 A in 0.5 s, what is the change of flux linkage with the other coil ?
Answer:
Given M = 1.5 A
di = 20 – 0 = 20 A
dt = 0.5 sec
e = M\(\frac{\mathrm{di}}{\mathrm{dt}}=\frac{\mathrm{d} \phi}{\mathrm{dt}}\)
dΦ = M.di = 1.5 × 20
dΦ = 30 wb

Question 17.
What are limitations of Bohr’s theory of hydrogen atom?
Answer:
Limitations of Bohr’s theory of Hydrogen atom:

1. This theory is applicable only to simplest atom like hydrogen, with Z = 1. The theory fails in case of atoms of other elements for which Z > 1.
2. The theory does not explain why orbits of electrons are taken as circular, while elliptical orbits are also possible.
3. Bohr’s theory does not say anything about the relative intensities of spectral lines.
4. Bohr’s theory does not take into account the wave properties of electrons.

Question 18.
Describe how a semiconductor diode is used as a half wave rectifier.
Answer:
Working of half wave rectifiers : A single diode is used in Half wave rectifier. It rectifies only positive half cycles of the input AC signals. The circuit diagram is as shown in fig.

The input AC signed is applied across the primaiy trans-former P. It induces AC voltage in secondary then the DC output is obtained across the load resistance ‘R_L‘. The AC voltage across the secondary changes polarity after every half cycle.

During the positive half cycle, the diode is in forward biased and current flows through it. During the negative half cycles, the diode is reverse biased and current does not flow through it.

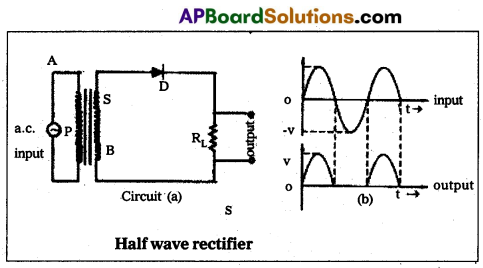
So, that current flows through the diode during positive half cycles only, current flows in R_L through one direction. Thus a Half wave rectifier gives discontinuous and pulsative DC output across the load resistance as shown in fig. The number of DC pulses per second is equal to frequency of the applied AC.

Efficiency of Rectifier: “The ratio of DC power output to the applied input AC power is known as Rectifier efficiency. It is denoted by ‘η’
∴ η = \(\frac{\text { DC power output }}{\text { AC power input }}\)
For Half wave Rectifier η = \(\frac{0.406 \times \mathrm{R}_{\mathrm{L}}}{\mathrm{r}_{\mathrm{f}}+\mathrm{R}_{\mathrm{L}}}\)

Section – C (2 × 8 = 16)

Note:

• Answer ANY TWO of the following questions.
• Each question carries EIGHT marks.
• ALL are long answer type questions.

Question 19.
Explain the formation of stationary waves in stretched strings and hence deduce the laws of transverse waves in stretched strings.
Answer:
A string is a metal wire whose length is large when compared to its thickness. A stretched string is fixed at both ends, when it is plucked at mid point, two reflected waves of same amplitude and frequency at the ends are travelling in opposite direction and overlap along the length. Then the resultant waves are known as the standing waves (or) stationary waves.

Let two transverse progressive waves of same amplitude a, wave length k and frequency V, travelling in opposite direction be given by
y₁ = a sin (kx – ωt) and y₂ = a sin (kx + ωt)
where ω = 2π v and k = \(\frac{2 \pi}{\lambda}\)
The resultant wave is given by y = y₁ + y₂
y = a sin (kx – ωt) + a sin (kx + ωt)
y = (2a sin kx) cos ωt
2a sin kx = Amplitude of resultant wave.

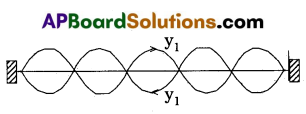
It depends on ‘kx’. If x = 0, \(\frac{\lambda}{2}, \frac{2 \lambda}{2}, \frac{3 \lambda}{2}\) … etc, the amplitude = zero
These position are known as “Nodes”.
If x = \(\frac{\lambda}{4}, \frac{3 \lambda}{4}, \frac{5 \lambda}{4}\) ……. etc, the amplitude = maximum (2a).
These positions are called “Antinodes”.

If the string vibrates in ‘P’ segments and ‘l’ is its length then length of each segment = \(\frac{l}{\mathrm{P}}\)
Which is equal to \(\frac{\lambda}{2}\)
∴ \(\frac{l}{\mathrm{P}}=\frac{\lambda}{2}\) ⇒ λ = \(\frac{2 l}{\mathrm{P}}\)
Harmonic frequency v = \(\frac{v}{\lambda}=\frac{v P}{2 l}\)
v = \(\frac{v \mathrm{P}}{2 l}\) ………….. (1)
If ‘T’ is tension (stretching force) in the string and ‘μ’ is linear density then velocity of transverse wave (v) in the string is
v = \(\sqrt{\frac{T}{\mu}}\) ……. (2)
From the Eqs (1) and (2)
Harmonic frequency v = \(\frac{\mathrm{P}}{2 l} \sqrt{\frac{\mathrm{T}}{\mu}}\)
If P = 1 then it is called fundamental frequency (or) first harmonic frequency
∴ Fundamental Frequency v = \(\frac{1}{2 l} \sqrt{\frac{\mathrm{T}}{\mu}}\) ………. (3)
If p = 2 then it is first overtone (or) second harmonic frequency.
v₁ = \(\frac{2}{2 l} \sqrt{\frac{\mathrm{T}}{\mu}}\)2v
Similarly if p = 3 then second overtone (or) third harmonic frequency.
v₂ = \(\frac{3}{2 l} \sqrt{\frac{\mathrm{T}}{\mu}}\)3v
from the Eqs (3), (4) and (5)
The ration of the frequencies of harmonics are
v : v₁ : v₂ : = v : 2v : 3v = 1 : 2 : 3
∴ The frequencies of the overtones in a given vibrating length, are integral multiples of the fundamental in the same length.

Laws of Transverse Waves Along Stretched String:
Fundamental frequency of the vibrating string v₂ = \(\frac{1}{2 l} \sqrt{\frac{\mathrm{T}}{\mu}}\)

First Law: When the tension (T) and linear density (μ) are constant, the fundamental frequency (v) of a vibrating string is inversely proportional to its length.
∴ v ∝ \(\frac{1}{\mathrm{~T}}\) ⇒ vl constant, when ‘T’ and ‘μ’ are constant.

Second Law: When the length (l) and its, linear density (m) are constant the fundamental frequency of a vibrating string is directly proportional to the square root of the stretching force (T).
∴ v ∝ √T ⇒ \(\frac{v}{\sqrt{T}}\) constant, when ‘l’ and ‘+’ are constant.

Third Law: When the length (1) and the tension (T) are constant, the fundamental frequency of a vibrating string is inversely proportional to the square root of the linear density (M).
v ∝ \(\frac{1}{\sqrt{\mu}}\) ⇒ v√μ constant, when ‘l’ and ‘T’ are constant.

Question 20.
State Kirchhoff s laws for an electrical network. Using these laws deduce the condition for balance in a Wheatstone bridge. TWo resistors of resistances 10 Ω and 15 Ω are connected in parallel. Find the effective resistance of their combination.
Answer:
1) Kirchhoffs first law (Junction rule or KCL) : The algebraic sum of the currents at any junction is zero.
∴ ΣI = 0
(or)
The sum of the currents flowing towards a junction is equal to the sum of currents away from the junction.

2) Kirchhoffs second law (Loop rule or KVL) : The algebraic sum of potential around any closed loop is zero.
∴ Σ(IR) + ΣE = 0

Wheatstone bridge: Wheatstone’s bridge circuit consists of four resistances R₁, R₂, R₃ and R₄ are connected to form a closed path. A cell of emf e is connected between the point A and C and a galvanometer is connected between the.points B and D as shown in fig. The current through the various branches are indicated in the figure. The current through the galvanometer is I_g and the resis¬tance of the galvanometer is G.

Applying Kirchhoff’s first la
at the junction D, I₁ – I₃ – I_g = 0 ………….. (1)
at the junction B, I₂ + I_g I₄ = 0 ………… (2)
⇒ Applying Kirchhoff s second law to the closed path ADBA,
– I₁R₁ – I_gG + I₂R₂ = 0
(or)
⇒ I₁ R₁ + I_gG = I₂R₂

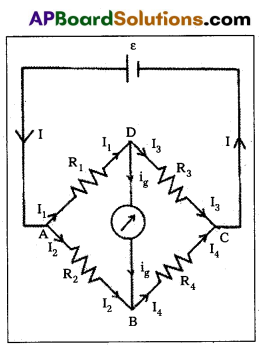
⇒ to the closed path DCBD
– I₃R₃ + I₄R₄ = I_gG = 0
⇒ I₃R₃ – I_gG = I₄R₄
⇒ When the galvanometer shows zero deflection the points D and B are at the same potential so I_g = 0.

Substituting this value in (1), (2), (3) and (4).
I₁ = I₃ ………… (5)
I₂ = I₄ …………….. (6)
I₁R₁ = I₂R₂ …………… (7)
I₃R₃ = I₄R₄ …………… (8)
⇒ Dividing (7) by (8)
\(\frac{I_1 R_1}{I_3 R_3}=\frac{I_2 R_2}{I_4 R_4}\) ⇒ \(\frac{R_1}{R_3}=\frac{R_2}{R_1}\) [∵ I₁ = I₃ & I₂ = I₄]
∴ Wheatstone’s Bridge principle :
R₄ = R₃ × \(\frac{\mathbf{R}_2}{\mathrm{R}_1}\)

Problem: R_p = \(\frac{R_1 R_2}{R_1+R_2}\)
Resistance of the long wire 4R
Hence, resistance of the half wire = \(\frac{4 \mathrm{R}}{2}\) = 2R When these two are connected in parallel, then the effective resistance
R_p = \(\frac{2 R \times 2 R}{2 R+2 R}=\frac{4 R^2}{4 R}\) = R

Problem: Two resistors of resistances 10 Ω and 15 Ω are connected in parallel. Find the effective resistance of their combination.
Solution:
Given, R₁ = 10Ω; R₂ = 15; R_p = ?
Effective resistance, in parallel
R_p = \(\frac{R_1 R_2}{R_1+R_2}\) = \(\frac{10 \times 15}{10+15}\) = \(\frac{10 \times 15}{25}\) = 6Ω

Question 21.
What, is radioactivity ? State the law of radioactive decay. Show that radioactive decay is exponential in nature.
The half life period of radium is 1600 years. How much time does 1 g of radium take to reduce to 0.125 g ?
Answer:
1. Radioactivity: The nuclei of certain elements disintegrate spontaneously by emitting alpha (α), beta (β) and gamma (γ) rays. This phenomenon is called Radioactivity or Natural radioactivity.

2. Law of radioactivity decay: “The rate of radioactive decay (\(\frac{\mathrm{dN}}{\mathrm{dt}}\)) (or) the number of nuclei decaying per unit time at any instant, is directly proportional to the number of nuclei (N) present at that instant is called law of radioactivity decay.”

3. Radioactive decay is exponential in nature : Consider a radioactive substance. Let the number of nuclei present in the sample at t = 0, be N₀ and let N be the radioactive nuclei remain at an instant t.
\(\frac{\mathrm{dN}}{\mathrm{dt}}\) ∝ N ⇒ N\(\frac{\mathrm{dN}}{\mathrm{dt}}\) = -λ
dN = -λNdt ………….. (1)
The proportionality constant λ is called decay constant or disintegration constant. The negative sign indi
cates the decrease in the number of nuclei.

4. From eq. (1) \(\frac{\mathrm{dN}}{\mathrm{N}}\) = – λ dt …………. (2)

5. Integrating on both sides
\(\int \frac{\mathrm{dN}}{\mathrm{N}}=-\lambda \int \mathrm{dt}\)
ln N = -λt + C ………… (3)
Where C = Integration constant.

6. At t = 0 N = N₀ Substituting in eq. (3), we get ln N₀ = C
∴ ln N = -λt + ln N₀
ln N – ln N₀ = -λt
ln (\(\frac{N}{N_0}\)) = -λt
∴ N = N₀e^-λt
The above equation represents radioactive decay law.

7. It states that the number of radioactive nuclei in a radioactive sample decreases exponentially with time.
The half life period of radium s 1600 years. How much time does lg of radium take to reduce to 0.125 g.
Answer:
Half life of radium = 1600 years
Initial mass = 1g
Final mass = 0.125 g
The quantity remaining after ‘n’ half lifes is \(\) of the initial quantity.
In this problem,
\(\frac{1}{2^n}\) = \(\frac{\text { quantity remaining }}{\text { Initial quantity }}\)
\(\frac{1}{2^n}\) = \(\frac{1}{4}+\frac{1}{v}=\frac{1}{\mathrm{f}}\) ∴ n = 3
∴ Time taken = ‘n’ half-lifes t = nx^t 1/2 = 3 × 1600
= 4,800 years