TS Inter 2nd Year Maths 2B Question Paper March 2019

Access to a variety of TS Inter 2nd Year Maths 2B Model Papers and TS Inter 2nd Year Maths 2B Question Paper March 2019 allows students to familiarize themselves with different question patterns.

TS Inter 2nd Year Maths 2B Question Paper March 2019

Time : 3 Hours
Max. Marks : 75

Section – A
(10 × 2 = 20)

I. Very Short Answer type questions.

1. Attempt all questions.
2. Each question carries two marks.

Question 1.
Write the parametric equations of the circle 2x² + 2y² = 7.
Solution:
Given circle equation is 2x² + 2y² = 7
⇒ x² + y² = \(\frac{7}{2}\)
Here centre (h, k) = (0, 0) and
radius r = \(\sqrt{\frac{7}{2}}\)
Circle Parametric equations are

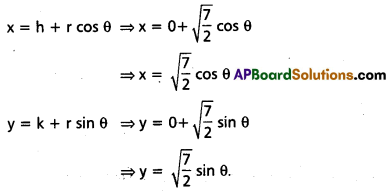
Question 2.
Find the value of k, if the points (1, 3) and (2, k) are conjugated with respect to the circle x² + y² = 35.
Solution:
Let S = x² + y² – 35= 0
Since the points (1, 3) and (2, k) are conjugated with respect to the circle S = 0
∴ S₁₂ = 0
⇒ x₁x₂ + y₁y₂ – 35 = 0
⇒ 2 + 3k – 35 = 0 ⇒ 3k = 33 ⇒ k = 11

Question 3.
Find the equation of radical axis of the circles x² + y² + 4x + 6y – 7 = 0, 4(x² + y²)+ 8x + 12y – 9 = 0.
Solution:
Let S ≡ x² + y² + 4x + 6y – 7 = 0,
S¹ ≡ x² + y² + 2x + 3y – \(\frac{9}{4}\) = 0
The equation of the radical axis of the circles S = 0, S¹ = 0 is S – S¹ = 0
⇒ (x² + y² + 4x + 6y – 7) – (x² + y² + 2x + 3y – \(\frac{9}{4}\)) = 0
⇒ x² + y² + 4x + 6y – 7 – x² – y² – 2x – 3y + \(\frac{9}{4}\) = 0
⇒ 8x + 12y – 19 = 0.

Question 4.
Find the equation of the normal to the parabola y² = 4x which is parallel to y – 2x + 5 = 0.
Solution:
Given parabola equation is y² = 4x
Here 4a = 4 ⇒ a = 1
Given line equation is y – 2x + 5 = 0
⇒ y = 2x – 5
∴ Slope m = 2
Since required normal is parallel to y = 2x – 5
∴ Slope of normal = 2
⇒ -t = 2 ⇒ t = -2
Equation of the normal at t is
y + xt = 2at + t³
⇒ y + x(-2) = 2(1) (-2) + (-2)³
⇒ y – 2x = -4 – 8
⇒ 2x – y – 12 = 0.

Question 5.
If the eccentricity of the hyperbola is \(\frac{5}{4}\), then find the eccentricity of its conjugate hyperbola.
Solution:
If e₁, e₂ are the eccentricities of hyperbola and conjugate hyperbola then \(\frac{1}{e_1^2}+\frac{1}{e_2^2}\) = 1

Question 6.
Evaluate \(\int \frac{1+\cos ^2 x}{1-\cos 2 x} d x\), on I ⊂ R\{nπ : n ∈ z}.
Solution:

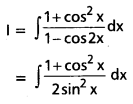
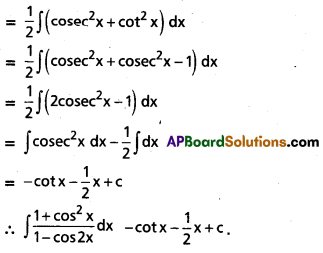
Question 7.
Evaluate \(\int \frac{1}{x \log x[\log (\log x)]}\)dx, on (1, ∝).
Solution:

Question 8.
Evaluate \(\int_0^a(\sqrt{a}-\sqrt{x})^2\) dx
Solution:

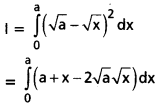
Question 9.
Find \(\int_0^{\pi / 2}\)cos¹¹ xdx.
Solution:

Question 10.
Find the general solution of : \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = \(\frac{2 y}{x}\)
Solution:
Given \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = \(\frac{2 y}{x}\) ……… (1)
⇒ \(\frac{\mathrm{dy}}{\mathrm{y}}\) = 2\(\frac{d x}{x}\)
2\(\frac{d x}{x}\) = \(\frac{d y}{y}\) = 0
Integrating

Section – B
(5 × 4 = 20)

II. Short Answer type questions.

1. Answer ANY FIVE questions.
2. Each question carries FOUR marks.

Question 11.
Find the equation of the circle which cuts orthogonally the circle x² + y² – 4x + 2y – 7 = 0 and having the centre at (2, 3).
Solution:
Let x² + y² + 2gx + 2fy + c = 0 be the required circle equation ………. (1)
Given centre (-g, -f) = (2, 3)
∴ -g = 2,-f = 3
⇒ g = -2, f = -3.
Given circle equation in x² + y² – 4x + 2y – 7 = 0 …….. (2)
Since (1), (2) cut orthogonally
∴ 2g₁g₂ + 2f₁f₂ = c₁ + c₂
⇒ 2(-2)(-2)+2(-3)(1) = -7 + c
⇒ 8 – 6 = -7 + c
⇒ 2 = -7 + c ⇒ c = 9
Hence required circle equation is
x² + y² + 2(-2)x + 2(-3)y + 9 = 0
⇒ x² + y² – 4x – 6y + 9 = 0.

Question 12.
The line y = mx + c and the circle x² + y² = a² intersect at A and B. If AB = 2λ, then show that:
c² = (1 + m²)(a² – λ²).
Solution:
Given circle equation is x² + y² = a²
Centre c = (0, 0) and radius r = a
d = The ⊥ distance from c to line
y = mx + c

Question 13.
Find the equation of the ellipse with focus at (1, -1), e = \(\frac{2}{3}\) and directrix as x + y + 2 = 0.
Solution:
Given focus s = (1, -1)
Eccentricity e = \(\frac{2}{3}\)
Equation of directrix is x + y + 2 = 0
Let P(x, y) be any point on the ellipse
\(\frac{S P}{P M}\) = e
⇒ SP = e.PM
⇒ SP² = e².PM²

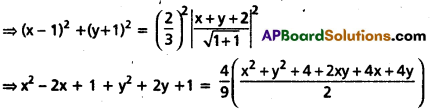
⇒ 9x + 9y² – 18x + 18y + 18 = 2x² + 2y² + 8 + 4xy + 8x + 8y
⇒ 7x² – 4xy + 7y² – 26x + 10y + 10 = 0
Hence required ellipse equation is
7x² – 4xy + 7y² – 26x + 10y + 10 = 0.

Question 14.
Find the equations of tangents to the ellipse 2x² + 3y² = 11 at the points whose ordinate is 1.
Solution:
Given ellipse equation is 2x² + 3y² = 11
Given ordinate y = 1
⇒ 2x² + 3 = 11
⇒ 2x² = 8
⇒ x² = 8
⇒ x = ±2
∴ Points on the ellipse are P(1, 2) and Q(-2, 1)

Case (i): P(2, 1)
∴ Equation of the tangent at P is S₁ = 0
⇒ 2x(2) + 3y(1) – 11 = 0
⇒ 4x + 3y – 11 = 0
∴ Equation of the normal at P is
3(x – 2) – 4(y – 1) = 0
⇒ 3x – 6 – 4y + 4 = 0
⇒ 3x – 4y – 2 = 0

Case (ii): Q (-2,1)
Equation of the tangent at Q is S₁ = 0
⇒ 2x(-2) + 3y(1) – 11 = 0
⇒ – 4x + 3y – 11 = 0
⇒ 4x – 3y + 11 = 0
Equation of the normal at Q is
3(x + 2) + 4(y – 1) = 0
⇒ 3x + 6 + 4y – 4 = 0
⇒ 3x + 4y + 2 = 0.

Question 15.
Find the foci, eccentricity, equations of the directrix, length of latus rectum of the hyperbola x² – y² = 4.
Solution:
Given equation of the hyperbola is x² – 4y² = 4
Here a² = 4, b² = 1
Centre = (0, 0)
Eccentricity e = \(\sqrt{\frac{a^2+b^2}{a^2}}\)
= \(\sqrt{\frac{4+1}{4}}\)
= \(\sqrt{\frac{5}{4}}\)
= \(\frac{\sqrt{5}}{2}\)

Question 16.
Find: \(\int_0^{2 \pi}\) sin⁴ x cos⁶ x dx.
Solution:

Question 17.
Solve the differential equation : cos x\(\frac{\mathrm{dy}}{\mathrm{dx}}\) + y sin x = sec² x.
Solution:
Given cos x\(\frac{d y}{d x}\) + y sin x = sec² x
⇒ \(\frac{d y}{d x}\) + y tanx = sec³x …….. (1)
Here P = tan x, Q = Sec³ x

Section – C
(5 × 7 = 35)

III. Long Answer type questions.

1. Answer ANY FIVE questions.
2. Each question carries SEVEN marks.

Question 18.
Show that the points (9, 1), (7, 9), (-2, 12), (6, 10) are concyclic and find the equation of the circle on which they lie.
Solution:
Let A = (9, 1), B = (7, 9), C = (-2, 12), D = (6, 10)
The equation of the circle which having \(\overline{\mathrm{AB}}\) as a diameter is
(x – x₁)(x – x₂) + (y – y₁)(y – y₂) = 0
⇒ (x – 9)(x – 7) + (y – 1 )(y – 9) = 0
⇒ x² – 7x – 9x + 63 + y² – 9y – y + 9 = 0
⇒ x² + y² – 16x – 10y + 72 = 0 ……… (1)
Slope of \(\overline{\mathrm{AB}}\) = \(\frac{y_2-y_1}{x_2-x_1}\) = \(\frac{9-1}{7-9}\) = \(\frac{8}{-2}\) = -4
Equation of \(\overline{\mathrm{AB}}\) is y – 1 = – 4(x – 9)
⇒ y – 1 = – 4x + 36
⇒ 4x + y – 37 = 0
The equation of circle passing through A, B is
(x² + y² – 16x – 10y + 72) + C(4x + y – 37) = 0
If this circle passes through C(-2, 12) then
4 + 144 + 32 – 120 + 72 + C(-8 + 12 – 37) = 0
⇒ 132 – 33C = 0
⇒ 33C = 132 ⇒ C = 4
∴ Equation of the circle passes through A, B, C is
(x² + y² – 16x – 10y + 72) + 4(4x + y – 37) = 0
⇒ x² + y² – 16x – 10y + 72 + 16x + 4y – 148 = 0
⇒ x² + y² – 6y – 76 = 0 ……….. (2)
x² + y² – 6y – 76 = (6)² + (10)² – 6(10) – 76
= 36 + 100 – 60 – 76 = 0
∴ D(6, 10) lies on (2)
∴ A, B, C, D are concydic and circle equation is x² + y² – 6y – 76 = 0.

Question 19.
Show that, four common tangents can be drawn for the circles given by x² + y² – 14x + 6y + 33 = 0 and x² + y² + 30x – 2y + 1 = 0 and find the internal and external centres of similitude.
Solution:
Given circle equations are x² + y² – 14x + 6y + 33 = 0
x² + y² + 30x – 2y + 1 = 0
Centres A = (7, -3), B = (-15, 1)
r₁ = \(\sqrt{49+9-33}\) = \(\sqrt{25}\) = 5

∴ Four tangents can be drawn for the given circles.
Let P, Q be the internal and external centres of similitude.
∴ P divides \(\overline{\mathrm{AB}}\) in the ratio 1 : 3 internally

Question 20.
From an external point ‘P’ tangents are drawn to the parabola y² = 4ax and these tangents make angles θ₁, θ₂ with its axis, such that cot θ₁ + cot θ₂ is a constant ‘d’. Then show that all such P lie on a horizontal line.
Solution:
Equation of a tangent to the Parabola y² = 4ax is a
y = mx + \(\frac{a}{m}\)
This tangent passes through P(x₁y,)
∴ y₁ = mx₁ + \(\frac{\mathrm{a}}{\mathrm{m}}\)
⇒ my₁ = m²x₁ + a
⇒ m²x₁ – my₁ + a = 0 which is a quadratic eq. in m
If m₁, m₂ are the slopes of the tangents drawn from P then m₁, m₂ are the roots of the equation m²x₁ – my₁ + a = 0

Question 21.
Evaluate : ∫e^ax sin(bx + c)dx; (a, b, c ∈ R; b ≠ 0) on R.
Solution:

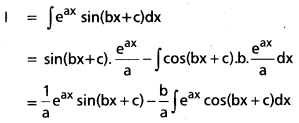
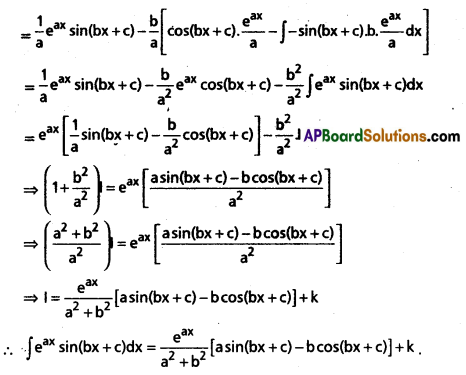
Question 22.
Obtain reduction formula for I_n = ∫cotⁿ x dx; n being a positive integer; n ≥ 2 and deduce the value of ∫cot⁴ x dx.
Solution:

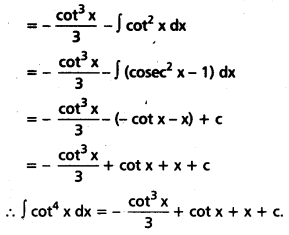
Question 23.
Find : \(\int_0^\pi x \sin ^7 x \cos ^6 x d x .\)
Solution:

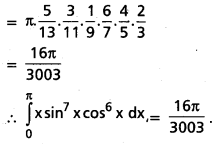
Question 24.
Solve the differential equation : \(\frac{d y}{d x}\) = \(\frac{2 y+x+1}{2 x+4 y+3}\)
Solution:


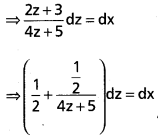
Integrating
\(\int \frac{1}{2} d z\) + \(\frac{1}{2} \int \frac{1}{4 z+5}\)dz = \(\int d x\) + \(\frac{c}{8}\)
⇒ \(\frac{1}{2}\)z + \(\frac{1}{2} \cdot \frac{1}{4}\)log|4z + 5| = x + \(\frac{c}{8}\)
⇒ 4z – log|4z + 5| = 8x + c
⇒ 4(x + 2y) + log|4(x + 2y) + 5| = 8x + c
⇒ 8y – 4x + log|4x + 8y + 5| = c
∴ The general solution of (1) is
8y – 4x + log|4x + 8y + 5| = c.