TS Inter 2nd Year Maths 2A Question Paper May 2016

Thoroughly analyzing TS Inter 2nd Year Maths 2A Model Papers and TS Inter 2nd Year Maths 2A Question Paper May 2016 helps students identify their strengths and weaknesses.

TS Inter 2nd Year Maths 2A Question Paper May 2016

Time: 3 Hours
Maximum Marks: 75

Note: This question paper consists of three Sections A, B, and C.

Section – A
(10 × 2 = 20 Marks)

I. Very Short Answer Type Questions.

• Answer all questions.
• Each question carries two marks.

Question 1.
Find a square root of 7 + 24i.
Solution:

Question 2.
Express 1 – i complex number in modulus amplitude form.
Solution:

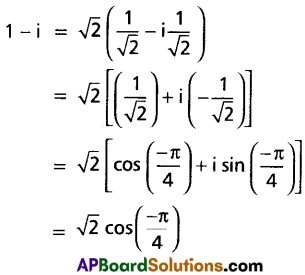
which is the required modulus amplitude form.

Question 3.
If x = cis θ, then find the value of \(\left(x^6+\frac{1}{x^6}\right)\).
Solution:
Given x = cis θ
⇒ x = cos θ + i sin θ
⇒ x⁶ = (cos θ + i sin θ)⁶ = cos 6θ + i sin 6θ
\(\frac{1}{x^6}=\frac{1}{\cos 6 \theta+i \sin 6 \theta}\) = cos 6θ – i sin 6θ
∴ x⁶ + \(\frac{1}{x^6}\) = cos 6θ + i sin 6θ + cos 6θ – i sin 6θ = 2 cos 6θ
∴ x⁶ + \(\frac{1}{x^6}\) = 2 cos 6θ

Question 4.
Form a quadratic equation whose roots are 7 ± 2√15.
Solution:
Let α = 7 + 2√5 and β = 7 – 2√5
α + β = 7 + 2√5 + 7 – 2√5 = 14
αβ = (7 + 2√5) (7 – 2√5)
= 49 – (2√5)²
= 49 – 4(5)
= 49 – 20
= 29
∴ Required quadratic equation is x² – (α + β)x + αβ = 0
⇒ x² – 14x + 29 = 0

Question 5.
If 1, 1, α are the roots of x³ – 6x² + 9x – 4 = 0, then find ‘α’.
Solution:
Given 1, 1, α are the roots of x³ – 6x² + 9x – 4 = 0
∴ The Sum of the roots = \(\frac{-(-6)}{1}\)
⇒ 1 + 1 + α = 6
⇒ a = 6 – 2
⇒ a = 4

Question 6.
Find the number of ways in which 4 letters can be put in 4 addressed envelopes so that no letter goes into the envelope meant for it.
Solution:
The number of ways in which 4 letters can be put in 4 addressed envelopes so that no letter goes into the envelope meant for it is \(4 !\left(\frac{1}{2 !}-\frac{1}{3 !}+\frac{1}{4 !}\right)\)
= \(24\left(\frac{1}{2}-\frac{1}{6}+\frac{1}{24}\right)\)
= 12 – 4 + 1
= 9 ways

Question 7.
Find the number of ways of arranging the letters of the word, ‘INDEPENDENCE’.
Solution:
The word INDEPENDENCE contains 12 letters in which there are 3N’s are alike 2D’s are alike 4E’s are alike and the rest are different.
∴ The no. of required arrangements = \(\frac{(12) !}{3 ! 2 ! 4 !}\)

Question 8.
If (1 + x + x²)ⁿ = α₀ + α₁x + α₂x² + ……… + α_2nx²ⁿ Prove that α₀ + α₁ + a₂ + ………. + α_2n = 3ⁿ.
Solution:
Given (1 + x + x²)ⁿ = a₀ + a₁x + a₂x² + ……… + a_2nx²ⁿ
Put x = 1
∴ (1 + 1 + 1)ⁿ = a₀ + a₁ + a₂ + ……….. a_2n
∴ a₀ + a₁ + a₂ + ………. + a_2n = 3ⁿ

Question 9.
Find the mean deviation from the mean of discrete data:
6, 7, 10, 12, 13, 4, 12, 16
Solution:
Given discrete data 6, 7, 10, 12, 13, 4, 12, 16
The A.M. of the given data
\(\bar{x}=\frac{6+7+10+12+13+4+12+16}{8}\)
= \(\frac{80}{8}\)
= 10
The absolute values of the deviations are |6 – 10|, |7 – 10|, |10 – 10|, |12 – 10|, |13 – 10|, |4 – 10|, |12 – 10|, |16 – 10| = 4, 3, 0, 2, 3, 6, 2, 6
∴ The mean deviation from the mean = \(\frac{1}{n} \in\left|x_i-\bar{x}\right|\)
= \(\frac{1}{8}\)(4 + 3 + 0 + 2 + 3 + 6 + 2 + 6)
= \(\frac{1}{8}\)(26)
= 3.25

Question 10.
A Poisson variable satisfies P(X = 1) = P(X = 2). Find P(X = 5).
Solution:
Given P(X = 1) = P(X = 2)

Section – B
(5 × 4 = 20 Marks)

II. Short Answer Type Questions.

• Attempt any five questions.
• Each question carries four marks.

Question 11.
If x + iy = \(\frac{1}{1+\cos \theta+i \sin \theta}\), then show that 4x² – 1 = 0.
Solution:

Now, equating real points on both sides, we Have
x = \(\frac{1}{2}\)
⇒ x² = \(\frac{1}{4}\)
⇒ 4x² = 1
⇒ 4x² – 1 = 0

Question 12.
If x is real, prove that \(\frac{x}{x^2-5 x+9}\) lies between \(-\frac{1}{11}\) and 1.
Solution:
Let y = \(\frac{x}{x^2-5 x+9}\)
⇒ yx² – 5xy + 9y = x
⇒ yx² + (-5y – 1)x + 9y = 0
x ∈ R ⇒ (-5y – 1)² – 4 . y . 9y ≥ 0
⇒ 25y² + 10y + 1 – 36y² ≥ 0
⇒ -11y² + 10y + 1 ≥ 0
⇒ 11y² – 10y – 1 ≤ 0
⇒ 11y² – 11y + y – 1 ≤ 0
⇒ 11y(y – 1) + 1(y – 1) ≤ 0
⇒ (11y + 1) (y – 1) ≤ 0
⇒ \(-\frac{1}{11}\) ≤ y ≤ 1
∴ \(\frac{x}{x^2-5 x+9}\) lies between \(-\frac{1}{11}\) and 1.

Question 13.
If the 6 letters of the word EAMCET are permuted in all possible ways and if the words thus formed are arranged in the dictionary order, find the rank of the word EAMCET.
Solution:
The dictionary order of the letters of the word EAMCET is A, C, E, E, M, T.
The no. of words that begin with
A – – – – – = \(\frac{5 !}{2 !}=\frac{120}{2}\) = 60
C – – – – – = \(\frac{5 !}{2 !}=\frac{120}{2}\) = 60
E A C – – – = 3! = 6
E A E – – – = 3! = 6
The next word is EAMCET = 1
Hence the rank of the word EAMCET is = 60 + 60 + 6 + 6 + 1 = 133.

Question 14.
Find the number of ways of selecting a cricket team of 11 players from 7 batsmen and 6 bowlers such that there will be at least 5 bowlers in the team.
Solution:
Since the team consists of atleast 5 bowlers, the selection may be of the following types.

	Batsmen (7)	Bowlers (6)
Type 1	6	5
Type 2	5	6

The no. of selections is first type = ⁷C₆ × ⁶C₅ = 7 × 6 = 42
The no. of selections in second type = ⁷C₅ × ⁶C₆ = 21 × 1 = 21
∴ The required number of ways of selecting the cricket team = 42 + 21 = 63

Question 15.
Resolve \(\frac{x^3}{(x-a)(x-b)(x-c)}\) into partial fractions.
Solution:
Let \(\frac{x^3}{(x-a)(x-b)(x-c)}=1+\frac{A}{x-a}+\frac{B}{x-b}+\frac{C}{x-c}\)
⇒ x³ = (x – a) (x – b) (x – c) + A(x – b) (x – c) + B(x – a) (x – c) + C(x – a) (x – b)
Put x = a
a³ = A(a – b)(a – c)
⇒ A = \(\frac{a^3}{(a-b)(a-c)}\)
Put x = b
b³ = B(b – a) (b – c)
⇒ B = \(\frac{b^3}{(b-a)(b-c)}\)
Put x = c
c³ = C(c – a) (c – b)
⇒ C = \(\frac{c^3}{(c-a)(c-b)}\)
∴ \(\frac{x^3}{(x-a)(x-b)(x-c)}\) = 1 + \(\frac{a^3}{(a-b)(a-c)(x-a)}\) + \(\frac{b^3}{(b-a)(b-c)(x-b)}+\frac{c^3}{(c-a)(c-b)(x-c)}\)

Question 16.
If A and B are independent events with P(A) = 0.6, P(B) = 0.7, then find
(i) P(A ∩ B)
(ii) P(A ∪ B)
(iii) P(B/A)
(iv) P(A^C ∩ B^C)
Solution:
Given A, B are independent events and P(A) = 0.6, P(B) = 0.7
(i) P(A ∩ B) = P(A) P(B)
= (0.6) (0.7)
= 0.42

(ii) P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= 0.6 + 0.7 – 0.42
= 0.88

(iii) P(B/A) = P(B) = 0.7

(iv) P(A^C ∩ B^C) = P(A^C) . P(B^C)
Since A^C and B^C are also independent events
= [1 – P(A)] [1 – P(B)]
= [1 – 0.6] [1 – 0.7]
= (0.4) (0.3)
= 0.12

Question 17.
If A and B are independent events of a random experiment, show that Ac and Bc are also independent.
Solution:
Given A and B are independent events.
∴ P(A ∩ B) = P(A) . P(B)
P(A^C ∩ B^C) = P[(A ∪ B)^C]
= 1 – P(A ∪ B)
= 1 – [P(A) + P(B) – P(A ∩ B)]
= 1 – [P(A) + P(B) – P(A) + P(B)]
= 1 – P(A) – P(B) + P(A) . P(B)
= [1 – P(A)] – P(B) [1 – P(A)]
= [1 – P(A)] [1 – P(B)]
= P(A^C) . P(B^C)
∴ A^C and B^C are also independent.

Section – C
(5 × 7 = 35 Marks)

III. Long Answer Type Questions.

• Attempt any five questions.
• Each question carries seven marks.

Question 18.
If α, β are the roots of the equation x² – 2x + 4 = 0, then for any n ∈ N, show that \(\alpha^n+\beta^n=2^{n+1} \cos \left(\frac{n \pi}{3}\right)\).
Solution:
Given x² – 2x + 4 = 0

Question 19.
Find the polynomial equation whose roots are the translates of those of the equation x⁴ – 5x³ + 7x² – 17x + 11 = 0 by -2.
Solution:
Let f(x) = x⁴ – 5x³ + 7x² – 17x + 11 = 0
The polynomial equation whose roots are translates of those of the equation f(x) = 0 by -2 is f(x + 2) = 0
⇒ (x + 2)⁴ – 5(x + 2)³ + 7(x + 2)² – 17(x + 2) + 11 = 0

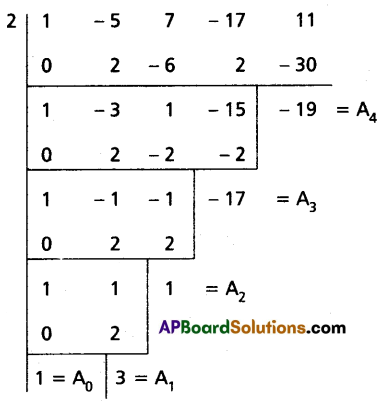
∴ Required equation is x⁴ + 3x³ + x² – 17x – 19 = 0

Question 20.
If the coefficients of r^th, (r + 1)^th, and (r + 2)^th terms in the expansion of (1 + x)ⁿ are in A.P. (Arithmetic Progression), then show that n² – (4r + 1)n + 4r² – 2 = 0.
Solution:
The coefficients of r^th, (r + 1)^th and (r + 2)^th terms in the expansion of (1 + x)³ are ⁿC_r-1, ⁿC_r, ⁿC_r+1 respectively.
Given ⁿC_r-1 + ⁿC_r+1 = 2 ⁿC_r are in A.P.
∴ ⁿC_r-1 + ⁿC_r+1 = 2 ⁿC_r

⇒ (n – r) (n – r + 1) = (r + 1) (2n – 3r + 2)
⇒ n² – 2nr + r² + n – r = 2nr – 3r² + 2r + 2n – 3r + 2
⇒ n² – 4nr + 4r² – n – 2 = 0
⇒ n² – (4r + 1)n + 4r² – 2 = 0

Question 21.
If x = \(\frac{1}{5}+\frac{1.3}{5.10}+\frac{1.3 .5}{5.10 .15}\) + ……..∞ then find 3x² + 6x.
Solution:

Question 22.
Find the mean deviation about the mean for the following data:

Marks Obtained	0-10	10-20	20-30	30-40	40-50
Number of Students	5	8	15	16	6

Solution:
Taking the assumed mean
a = 25 and h = 10
Construct the table

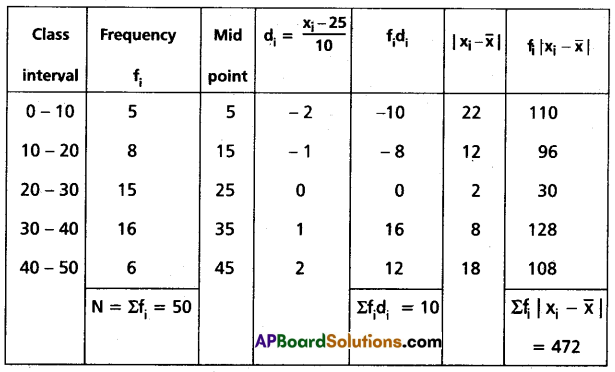
Question 23.
State and prove the addition theorem on probability.
Solution:
Statement: If E₁ and E₂ are any two events of a random experiment and P is the probability function.
Then P (E₁ ∪ E₂) = P(E₁) + P(E₂) – P(E₁ ∩ E₂)
Case (i): When E₁ ∩ E₂ = φ
E₁ ∩ E₂ = φ
⇒ P(E₁ ∩ E₂) = 0
∴ P(E₁ ∪ E₂) = P(E₁) + P(E₂) [∵ from the union axiom]
= P(E₁) + P(E₂) – 0
= P(E₁) + P(E₂) – P(E₁ ∩ E₂)
Case (ii): When E₁ ∩ E₂ = φ
E₁ ∪ E₂ can be expressed as union of 2 mutually exclusive events E₁ – E₂, E₂.
Hence, E₁ ∪ E₂ = (E₁ – E₂) ∪ E₂ also (E₁ – E₂) ∩ E₂ = φ
∴ P(E₁ ∪ E₂) = P[(E₁ – E₂) ∪ E₂] = P(E₁ – E₂) + P(E₂) …….(1) [∵ From the union axiom]
Also, E₁ can be expressed as union of 2 mutually exclusive events E₁ – E₂, E₁ ∩ E₂
Hence, E₁ = (E₁ – E₂) ∪ (E₁ ∩ E₂), also (E₁ – E₂) ∩ (E₁ ∩ E₂) = φ
∴ P(E₁) = P[(E₁ – E₂) ∪ (E₁ ∩ E₂)] = P(E₁ – E₂) + P(E₁ ∩ E₂)
⇒ P(E₁ – E₂) = P(E₁) – P(E₁ ∩ E₂)
∴ From (1), P(E₁ ∪ E₂) = P(E₁) – P(E₁ ∩ E₂) + P(E₂) = P(E₁) + P(E₂) – P(E₁ ∩ E₂)

Question 24.
A cubical die is thrown. Find the mean and variance of X, giving the number on the face that shows up.
Solution:
Let S be the sample space and X be the number on the face that shows up when a cubical die is thrown.