TS Inter 1st Year Physics Question Paper March 2017

Thoroughly analyzing TS Inter 1st Year Physics Model Papers and TS Inter 1st Year Physics Question Paper March 2017 helps students identify their strengths and weaknesses.

TS Inter 1st Year Physics Question Paper March 2017

Time: 3 Hours
Maximum Marks: 60

Section – A (10 × 2 = 20)

Note :

• Answer all questions.
• Each question carries two marks.
• All are very short answer type questions.

Question 1.
What is the discovery of C.V. Raman ?
Answer:
In elastic scattering of light by molecules.

Question 2.
How can systematic errors be minimized or eliminated ?
Answer:
Systematic errors can be minimised by improving experimental techniques, selecting better instruments and removing personal bias as far as possible. For a given set up, these errors may be estimated to a certain extent and the necessary corrections may be applied to the readings.

Question 3.
\(\vec{A}\) = \(\vec{i}\) + \(\vec{j}\). What is the angle between a Vector and the X-axis ?
Answer:
\(\vec{A}\) = \(\vec{i}\) + \(\vec{j}\)
cos α = \(\frac{A x}{|A|}\) (∵ A_x = 1)
= \(\frac{1}{\sqrt{1^2+1^2}}\) = \(\frac{1}{\sqrt{2}}\) ; α cos^-1 (\(\frac{1}{\sqrt{2}}\)) = 45°

Question 4.
What is inertia ? What gives the measure of inertia ?
Answer:
The resistance of the body to change its state of rest or state of uniform motion in a straight line is called inertia of the body.
Acceleration = \(\frac{\text { Force }}{\text { Mass }}\)
∴ The more is the mass, less is the acceleration and more is the inertia. The mass of a body is a quantitative measure of its inertia.

Question 5.
What is the principle behind the carburettor of an automobile ?
Answer:
The carburetor of automobile has a venturi channel (nozzle) through which air flows with a large speed. The pressure is then lowered at the narrow neck and the pertrol is sucked up in the chamber to provide the correct mixture, of air to fuel necessary for combustion.

Question 6.
Give the expression for the excess pressure in a liquid drop. Mention the terms in the expression.
Answer:
Excess pressure in a liquid drop, p_i – p₀ = \(\frac{2 s}{r}\)
where s = Surface tension; r = Radius of the liquid drop.

Question 7.
The roof of the buildings are often painted white during summer. Why ?
Answer:
The roof of buildings are painted white during summer, because it reflects more heat radiations and absorbs less heat radiations. Hence we feel comfort inside the house.

Question 8.
Why is it easier to perform the skating on the snow ?
Answer:
Due to excess pressure inside the liquid drop (p = \(\frac{2 T}{r}\)). Small ice particles acts as hard balls. So skating on snow is easy.

Question 9.
Define Mean free path.
Answer:
The average distance covered by a molecule between two successive collisions is called the mean free path.

Question 10.
State Dalton’s law of partial pressures.
Answer:
The total pressure exerted by a mixture of non-reacting gases occupying a vessel is equal to the sum of the individual pressures which each gas would exert if it alone occupied the whole vessel.
i.e., P = P₁ + P₂ + ……..

Section – B (6 × 4 = 24)

Note:

• Answer any six questions.
• Each question carries four marks.
• All are short answer type questions.

Question 11.
A parachutist flying in an aeroplane jumps when it is at a height of 3 km above the ground. He opens his parachute when he is about 1 km above ground. Describe his motion.
Answer:

• A parachutist is jumping from an air-plane at a height of 3 km from the ground. Up to 1 km above the ground, his motion is like a freely falling body. He falls with constant acceleration 9.8 ms^-2.
• At a height of 1 km above the ground, when he opened the parachute, the air drag opposes the force of gravity resultant on it. The acceleration of parachutist gradually decreases since velocity increases (a = g – bv) and becomes zero.
• Further, the parachutist attains terminal speed (constant speed), where air drag (in upward direction) is equal to force of gravity (in downward).
• Hopefully this terminal speed is slow enough, so he can touch the ground without much difficulty

Question 12.
State Parallelogram Law of Vectors. Derive an expression for the magnitude and direction of the resultant vector.
Answer:
“If two vectors acting at a point be represented in magnitude and direction by the two adjacent sides of a parallelogram, then their resultant is represented in magnitude and direction by the diagonal of the parallelogram passing through the same point”.

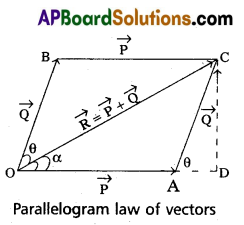
Explanation : \(\overrightarrow{\mathrm{P}}\) and \(\overrightarrow{\mathrm{Q}}\) are two vectors acting at a point ‘O’ with an angle ‘θ’ between them. \(\overrightarrow{\mathrm{OA}}\) and \(\overrightarrow{\mathrm{OB}}\) represent \(\overrightarrow{\mathrm{P}}\) and \(\overrightarrow{\mathrm{Q}}\) in magnitude and direction. Parallelogram OACB is completed. The diagonal OC represents the resultant of \(\overrightarrow{\mathrm{P}}\) and \(\overrightarrow{\mathrm{Q}}\) in magnitude and direction.

Magnitude of the resultant: OA is produced and perpendicular CD is drawn to it in the triangle ODC.
OC² = OD² + CD²
= (OA + AD)² + CD²
= OA² + AD² + 2 OA. AD + CD²
But in triangle CAD
AD² + CD² = AC²
cos θ = \(\frac{A D}{A C}\)
⇒ AD = AC cos θ
OC² = OA² + AC² + 2 OA. AD
R² = p² + Q² + 2PQ cos θ
R = \(\sqrt{P^2+Q^2+2 P Q \cos \theta}\)

Resultant direction :
From Δ^le COD
Tan α = \(\frac{C D}{O D}\) = \(\frac{C D}{O A+A D}\)
From AD = AC cos θ = Q cos θ
and CD = Q sin θ
∴ Tan α = \(\frac{Q \sin \theta}{P+Q \cos \theta}\)

Question 13.
Explain the advantages and disadvantages of friction.
Answer:
Advantages of friction :

1. Safe walking on the floor, motion of vehicles etc., are possible only due to friction.
2. Nails, screws are driven into walls (or) wooden surfaces due to friction.
3. Friction helps the fingures hold the things (or) objects like pen, pencil and water tumbler etc.
4. Speed running vehicles etc. can be stopped suddenly when friction is present, otherwise accidents become large. Due to friction vehicles move on the roads without slipping and they can be stopped.
5. The mechanical power transmission of belt drive is possible due to friction.

Question 14.
Define angular velocity and derive v = rω.
Answer:
The rate of change of angular displacement of a body is called angular velocity, i.e., ω = \(\frac{\mathrm{d} \theta}{\mathrm{dt}}\).
Derivation of v = rω : Consider a rigid body be moving with uniform speed (v) along the circumference of a circle of radius r. Let the body be displaced from A to B in a small interval of time Δt making an angle of Δθ at the centre. Let the linear displacement be Δx from A to B.
From the property, length of arc = radius × angle
Δ x = r Δ θ
This equation is divided by Δt and taking limit Δt → 0 on both sides.

∴ v = rω

Question 15.
Define vector product. Explain the properties of a vector product with two examples;
Answer:
The cross product of two vectors is given by \(\vec{C}\) = \(\vec{A}\) × \(\vec{B}\) The magnitude of the vector defined from cross product of two vectors is equal to product of magnitudes of the vectors and sine of angle between the vectors.

Direction of the vectors is given by right hand corkscrew rule and is perpendicular to the plane containing the vectors.
∴ | \(\vec{C}\) | = AB sin θ. and \(\vec{C}\) = AB sin θ n̂.
When, n̂ is the unit vector perpendicular to the plane containing the vectors \(\vec{A}\) and \(\vec{B}\)

Example :
1) Torque is cross product of position vector and Force.
i.e., \(\vec{T}\) = \(\vec{r}\) × \(\vec{F}\)

2) Angular momentum is cross product of position vector and momentum
i.e., \(\vec{L}\) = \(\vec{r}\) × \(\vec{P}\)

Properties :
1) Cross product does not obey commutative law. But its magnitude obey’s commutative law.
\(\vec{A}\) × \(\vec{B}\) ≠ \(\vec{B}\) × \(\vec{A}\) ⇒ (\(\vec{A}\) × \(\vec{B}\)) = – (\(\vec{B}\) × \(\vec{A}\)) , |(\(\vec{A}\) × \(\vec{B}\))| = |(\(\vec{B}\) × \(\vec{A}\))|

2) It obeys distributive law \(\vec{A}\) × (\(\vec{B}\) × \(\vec{C}\)) = \(\vec{A}\) × \(\vec{B}\) + \(\vec{A}\) × \(\vec{C}\)

3) The magnitude of cross product of two vectors which are parallel is zero.
Since θ = 0; | \(\vec{A}\) × \(\vec{B}\) | = AB sin 0° = 0

4) For perpendicular vectors, θ = 90°,
| \(\vec{A}\) × \(\vec{B}\) | = AB sin 90° | n̂ | = AB

Question 16.
State Kepler’s laws of planetary motion.
Answer:

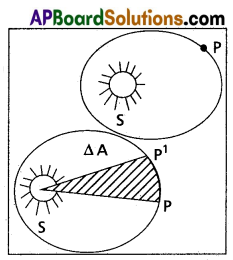
The three laws of Kepler can be stated as follows.

1. Law of orbits : All planets move in elliptical orbits with the sun situated at one of the foci.
2. Law of areas : The line that joins any planet to the sun sweeps equal areas in equal intervals of time.
3. Law of periods : The square of the time period of revolution of a planet is proportional to the cube of the semi-major axis of the ellipse traced out by the planet. T² α R³.

Question 17.
Describe the behaviour of a wire under gradually increasing load.
Answer:
Behaviour of a wire under the action of gradually increasing load :
When the load, is increased in steps, a graph is drawn between stress in Y-axis and corresponding strain on X-axis. Then the curve obtained is as shown in the figure. When a wire be clamped at one end and loaded at the other end, it undergoes four following steps.

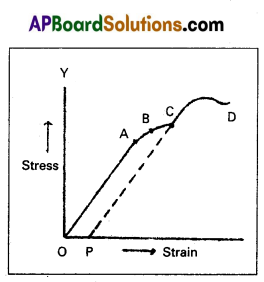
1) Proportional limit : In the linear position OA, stress is proportional to strain i.e., Hooke’s law is obeyed by the wire upto the point ‘A’, the graph is a straight line. Whenever the stretching force at ‘A’ is removed the wire regains its original length. ‘A’ is called proportional limit.

2) Elastic limit : In the graph ‘B’ is the elastic limit. Though the , wire doesn’t obey Hooke’s law at ‘B’, the wire regains its original length after removing the stretching force at ‘B’. Up to point ‘B’ the wire is under elastic behaviour.

3) Permanent set (or) yield point : In the graph ‘C’ is the yield point. If the stretching force at ‘C, is removed the wire doesn’t regain its original length and the length of the wire changes permanently. In this position the wire flows like a viscous liquid. After the point ‘C’, the wire is under plastic behaviour. ‘C’ is called permanent set or yield point.

4) Breaking point : When the stress increases the wire becomes thinner and thinner. When the stress increases to a certain limit the wire breaks. The stress at which the wire breaks is called Breaking stress and the point ‘D’ is called Breaking point.

5) Elastic fatigue : The state of temporary loss of elastic nature of a body due to continuous strain is called elastic fatigue. When a body is subjected to continuous strain within the elastic limit it appears to have lost elastic property temporarily to some extent and becomes weak.

Question 18.
Pendulum clocks generally go fast in winter and slow in summer. Why ?
Answer:
The time period of a pendulum at t₁ °C is T₁ = 2π \(\sqrt{\frac{L_1}{g}}\) ……….. (1)
Where L₁ is length of pendulum at t₁ °C.
If L₂ is length of pendulum at t₂°C,
then T₂ = 2π \(\sqrt{\frac{L_2}{g}}\) ………… (2)
\(\frac{(2)}{(1)}\) gives \(\frac{T_2}{T_1}\) = \(\sqrt{\frac{L_2}{L_1}}\) = \(\sqrt{\frac{L_1(1+\alpha t)}{L_1}}\)
Where α is the linear coefficient of expansion of pendulum clock. Where t = t₂ – t₁.

Due to expansion in length, during summer, time period increases or the clock looses time in summer. In winter due to fall in temperature, the length contracts, time period decreases, hence clock gains time.

Section – C (2 × 8 = 16)

Note :

• Answer any two questions.
• Each question carries eight marks.
• All are long answer type questions.

Question 19.
State and prove Law of Conservation of Energy in case of a freely falling body.
Answer:
Statement: Energy can neither be created nor destroyed, but it can be converted from one form to another form. The total energy of a system always remains constant.

Verification in the case of freely falling body : Let a body of mass ‘m’ be at a height ‘h’ above the ground. When it is freely falling with an acceleration due to gravity ‘g’, the potential energy gradually decreases and at the same time the K.E. of the body increases.

When the body is at A :
At the highest point final velocity v = 0
Kinetic energy K.E. = \(\frac{1}{2}\) mv² = 0
Potential energy P.E. = mgh
Total energy at
A = E= P.E. + K.E. = mgh + 0
∴ Total energy at A, E = mgh ________ (1)

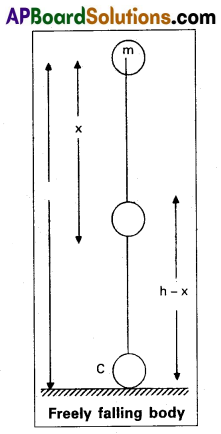
When the body is at B :
As the body falls freely, after travelling a distance x, reaches the point B.
At ‘B’ the body possesses both P.E. and K.E.
Potential energy P.E. = mg (h – x)
P.E = mgh – mgx
Kinetic energy K.E. = \(\frac{1}{2} m v_1^2\)
Total energy at B = P.E + K.E.
= mgh – mgx + \(\frac{1}{2} m v_1^2\)
For freely falling body
s = x
u = 0
v = v₁
a = g
Substitute these values in eqn.
v² – u² = 2as
\(v_1^2\) – 0² = 2gx.
\(v_1^2\) = 2gx
Total energy at
B = mgh – mgx + \(\frac{1}{2}\) m.2gx
= mgh – mgx + mgx = mgh
∴ Total energy at B, E = mgh ________ (2)

When the body is at C :
The body falls through a distance of ‘h’ and touches the ground at C with a velocity v₂.
Potential energy at C = mg = 0
Kinetic energy K.E. = \(\frac{1}{2} m v_2^2\)
Total energy at C = 0 + \(\frac{1}{2} m v_2^2\) = \(\frac{1}{2} m v_2^2\)
For freely falling body s = h, u = 0, v = v₂ a = g
Substitute these values in eqn. v² – u² = 2as ; \(v_2^2\) – 0² = 2gh
\(v_2^2\) = 2gh
Substitute this value in total energy, we get
Total energy at C = \(\frac{1}{2} m v_2^2\) = \(\frac{1}{2}\) m 2gh
∴ Total energy at C = mgh
In the above three cases total energy of the body is proved constant. Hence law of conservation of energy is proved.

Question 20.
Show that the motion of a simple pendulum is simple harmonic and hence derive an equation for its time period. What is seconds pendulum ? Calculate the length of the seconds pendulum.
Answer:

• Consider simple pendulum, a small bob of mass m tied to an inextensible mass less string of length L and other end of the string is fixed from a rigid support.
• Once the bob is slightly displaced and released, it begins to oscillate about mean position.
• Let θ be the angular displacement and T be the tension in the string.
• The forces acting on the bob are
  (a) tension T along the strin
  (b) weight mg acts vertically downwards.
• The force mg can be resolved into two components
  1. mg cos θ along the PA and
  2. mg sin θ acts along PB.
• From figure at point P,
  T = mg cos θ ________ (1)
• The force mg sin θ will provide the restoring torque, which tends to bring the bob back to its mean position O.
• The restoring torque is given by
  τ = Restoring force × ⊥^lar distance
  τ = – mg sin θ × L ________ (2)

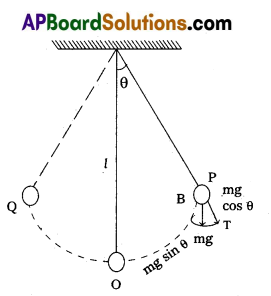
Here, negative sign shows that the torque acts to reduce θ.
Then sin θ is replaced by θ i.e., sin θ ≈ θ
τ = – mg L θ ________ (3)
(∵ sin θ = θ – \(\frac{\theta^3}{3 !}\) + \(\frac{\theta^5}{5 !}\) …… )

• From equation (3), we note that τ ∝ θ and this τ will bring the bob back towards its equilibrium position.
  So, if the bob is left free, it will execute angular simple harmonic motion.
  Comparing equation (3), with the equation τ = – kθ, we have spring factor,
  k = mgl.
• Here inertia factor = Moment of inertia of the bob about the point of suspension = mL²
• In S.H.M, Time period (T) = 2π \(\sqrt{\frac{\text { Inertia factor }}{\text { Spring factor }}}\)
  T = 2π \(\sqrt{\frac{\mathrm{mL}^2}{\mathrm{mgL}}}\)
  T = 2π \(\sqrt{\frac{L}{g}}\) ________ (4)
  Seconds pendulum : A pendulum whose time period is 2 seconds is called seconds pendulum.
  T = 2 seconds.

Problem :
T = 2 sec,
g = 9.8 m/s²
T = 2π\(\sqrt{\frac{l}{g}}\)
2 = 2π\(\sqrt{\frac{l}{9.8}}\)
l = \(\frac{9.8}{(3.14)^2}\) ≈ 1 m (or) 100 cm

Question 21.
Explain reversible and irreversible process. Describe the working of Carnot Engine. Obtain an expression for its efficiency.
Answer:
Reversible process : A process that can be retraced back in the opposite direction in such away that the system passes through the same states as in the direct process, and finally the system and the surroundings return in their original states, is called a reversible process.
A reversible process is only a purely idealised process.

Examples :

1. Slow isothermal and slow adiabatic changes.
2. Peltier effect and seeback effect.
3. Fusion of ice and vaporisation of water.

Irreversible process : “A process that cannot be retraced back in the opposite direction” is called as irreversible process.

In this process the system does not pass through the same intermediate states as in the reversible process.
All natural processes such as conduction, radiation, radioactivity etc, are irreversible.

Example :

1. Work done against friction.
2. Heat produced in conductors by passing a current through it. (Joule heating)
3. Diffusion of gases.

Carnot Engine : A reversible heat engine operating between two temperatures is called a carnot engine. The cycle operating it is known as carnot’s cycle. In this cycle the working substance (say an ideal gas) is taken through a cycle by means of two isothermals and two adiabatics. The four operations are shown in P – V (Indicator) diagram.

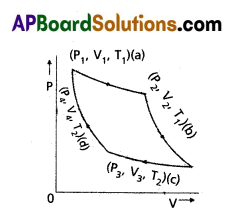
Step 1 → 2 : Isothermal expansion of the gas taking its state from (P₁, V₁ T₁,) to (P₂, V₂, T). It is shown in curve (a)
The heat absorbed by the gas (Q₁) from the reservoir at temperature T₁ equals the workdone by the gas. i.e.
W_{1 → 2} = Q₁ = µRT₁log_e(\(\frac{V_2}{V_1}\)) ________ (1)

Step 2 → 3 : Adiabatic expansion of the gas from (P₂, V₂, T₁,) to (P₃, V₃, T₂). It is shown in curve (b). The work done by the gas is given by
W_{2 → 3} = \(\frac{\mu R\left(T_1-T_2\right)}{(r-1)}\)

Step 3 → 4 : Isothermal compression of the gas from (P₃, V₃, T₂) to (P₄ , V₄, T₂). It is shown in curve (c). Heat released (Q₂) by the gas to the reservoir at temperature T₂ equals the work done on the goes.
i.e., W_{3 → 4} = µRT₂log_e(\(\frac{V_4}{V_3}\)) = – µRT₂log_e(\(\frac{V_3}{V_4}\)

Step 4 → 1 : Adiabatic compression of the gas from (P₄ , V₄, T₂) to (P₁, V₁, T₁). It is shown in curve (d) Work done on the gas is given by.
W_{3 → 4} = µR\(\frac{\left(T_2-T_1\right)}{(r-1)}\) = – µR\(\frac{\left(T_1-T_2\right)}{(r-1)}\)
Total workdone by the gas in one complete cycle is
W = W_{1 → 2} + W_{2 → 3} + W_{3 → 4} + W_{4 → 1}