TS 10th Class Maths Model Paper Set 3 with Solutions

The strategic use of TS 10th Class Maths Model Papers Set 3 can significantly enhance a student’s problem-solving skills.

TS SSC Maths Model Paper Set 3 with Solutions

Time: 3 Hours
Maximum Marks: 80

General Instructions:

1. Answer all the questions under Part – A on a separate answer book.
2. Write the answers to the questions under Part – B on the question paper itself and attach it to the the answer book of Part A.

Part – A (60 Marks)
Section – I (6 × 2 = 12 Marks)

Note :

1. Answer ALL the following questions.
2. Each question carries 2 marks.

Question 1.
Check whether A = {x : x² = 25 and 6x = 15} is an empty set or not ? Justify your answer.
Solution:
x² = 25 . ∴ x = \(\sqrt{25}\) = ± 5
6x = 15 ∴ x = \(\frac{15}{6}\) = \(\frac{5}{2}\)
Any value of x is not satisfying the above two equations. So, A is empty set.

Question 2.
Find two numbers whose sum is 27 and product is 182.
Solution:
Let the first number = x
∴ Second number = 27 – x
Product of two numbers = 182
x(27 – x) = 182
27x – x² = 182
⇒ x² – 27x + 182 = 0
⇒ x² – 13x – 14x + 182 = 0
⇒ x(x- 13) – 14(x – 13) = 0
⇒ (x – 13) (x – 14) = 0
⇒ x – 13 = 0 (or) x – 14 = 0
⇒ x = 13 (or) x = 14
∴ If first number =13, then second number = 27 – 13 = 14
If first number =14, then second number = 27 – 14 = 13
∴ Required numbers = 13 and 14.

Question 3.
Verify that the points (1, 5), (2, 3) and (-2, -1) are collinear are not.
Solution:
Let A(1, 5), B(2, 3), C(-2, -1)
Area of ΔABC
= \(\frac{1}{2}\)|x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)|
= \(\frac{1}{2}\)|1[3 – (- 1)] + 2[- 1 – 5] + (- 2) [5 – 3]|

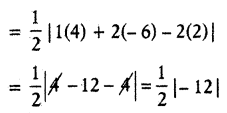
= \(\frac{1}{2}\) × 12 = 6 sq.units
Area of ΔABC ≠ 0
∴ Given points (1, 5), (2, 3) and (-2,-1) are not collinear.

Question 4.
A person from the top of a building of height 25 m has observed another building top and bottom at an angle of elevation 45° and at an angle of depression 60° respectively. Draw a diagram for this data.
Solution:

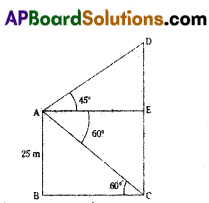
Question 5.
Find the area of required cloth to cover the heap of grain in conical shape, of whose diameter is 8m and slant height of 3m.
Solution:
Diameter of conical shape (heap of grain) (d) = 8m
Radius (r) = \(\frac{8}{2}\) = 4 m
Slant height l = 3m
L.S.A of the conical shape (heap) = πrl
= \(\frac{22}{7}\) × 4 × 3
= \(\frac{264}{7}\) = 37.71 m²
∴ Area of required cloth to cover the heap of grain = 37.71 m²

Question 6.
ΔABC ~ ΔDEF and their areas are respectively 64 cm² and 121 cm².
If EF = 15.4 cm., then find BC.
Solution:
\(\frac{{ar}(\triangle \mathrm{ABC})}{{ar}(\triangle \mathrm{DEF})}\) = \(\left(\frac{B C}{E F}\right)^2\)
\(\frac{64}{121}\) = \(\left(\frac{B C}{15.4}\right)^2\)
= \(\frac{8}{11}\) = \(\frac{B C}{15.4}\)
⇒ BC = \(\frac{8 \times 15.4}{11}\) = 11.2 cm

Section – II (6 × 3 = 18 Marks)

Note :

1. Answer ALL the following questions.
2. Each question carries 2 marks.

Question 7.
Check whether the given pair of linear equations represent intersecting, parallel or coincident lines. Find the
solution if the equations are consistent.
i) 3x + 2y = 5 ; 2x – 3y = 7
ii) 2x – 3y = 5 ; 4x -6y = 15
Solution:
Given pair of linear equations
i) 3x + 2y = 5 …………….. (1)
2x – 3y = 7 …………….. (2)
3x + 2y – 5 = 0
2x – 3y – 7 = 0
a₁ = 3, b₁ = 2, c₁ = -5
a₂ = 2, b₂ = -3, c₂ -7
\(\frac{a_1}{a_2}\) = \(\frac{3}{2}\), \(\frac{b_1}{b_2}\) = \(\frac{2}{-3}\)
\(\frac{a_1}{a_2}\) ≠ \(\frac{b_1}{b_2}\)
∴ Given pair of linear equations rep-resent intersecting lines.
∴ Given equations are consistent.

ii) 2x – 3y = 5 ………….. (3)
4x – 6y = 15 …………… (4)
2x – 3y – 5 = 0
4x – 6y – 15 = 0
a₁ = 2, b₁ = -3, c₁ = -5
a₂ = 4, ₂ = -6, c₂ = -15
\(\frac{a_1}{a_2}\) = \(\frac{2}{4}\) = \(\frac{2}{4}\),
\(\frac{b_1}{b_2}\) = \(\frac{-3}{-6}\) = \(\frac{1}{2}\)
\(\frac{c_1}{c_2}\) = \(\frac{-5}{-15}\) = \(\frac{1}{3}\)
\(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) ≠ \(\frac{c_1}{c_2}\)
∴ Given pair of linear equations represent parallel lines.
∴ Given equations are inconsistent.

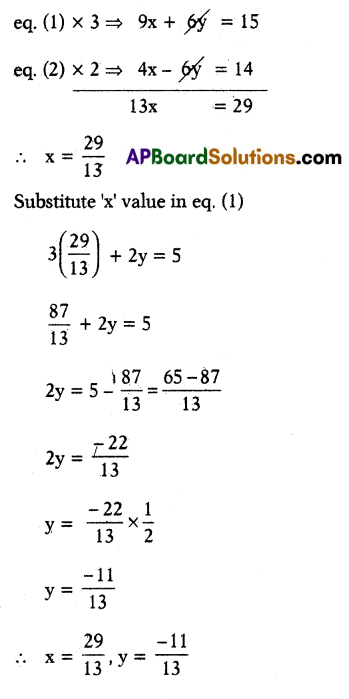
Question 8.
The 10^th term of an AP is 52 and 16^th term is 82, then find the 32^nd term.
Solution:
Given : An AP where
10^th term = 52
16^th term = 82

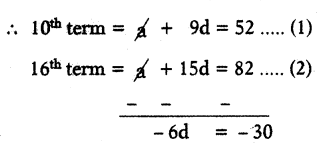
⇒ -6d = -30
⇒ d = \(\frac{-30}{-6}\) = 5
Substituting d = 5 in the equation (1) we get
a + 9d = 52
a + 9 × 5 = 52
⇒ a + 45 = 52 ⇒ a = 52 – 45 = 7
Now 32^nd term = a + 31 d
= 7 + 31 × 5.
= 7 + 155 = 162

Question 9.
Find the zeroes of the quadratic polynomial x² + 5x + 6 and verify the relationship between the zeroes and coefficients.
Solution:
p(x) = x² + 5x + 6
If p(x) = 0, then x² + 5x + 6 = 0
x² + 2x + 3x + 6 = 0
x(x + 2) + 3(x + 2) = 0
(x + 2) (x + 3) = 0
x + 2 = 0 (or) x + 3 = 0
x = -2 (or) x = -3
∴ Zeroes of p(x) = -2, -3
Let α = -2 and β = -3
Sum of the zeroes α + β = (- 2) + (- 3)
= -5

Question 10.
A toy is in the form of a cone mounted on a hemisphere. The diameter of the base and the height of the cone are 6 cm and 4 cm respectively. Find the surface area of the toy. (Take π = 3.14)
Solution:
Diameter of the base of the cone d = 6 cm.
∴ Radius of the base of the cone.
r = \(\frac{d}{2}\) = \(\frac{1}{2}\) = 3 cm.

Height of the cone = h = 4 cm
Slant height of the cone
l = \(\sqrt{r^2+h^2}\)
= \(\sqrt{(3)^2+(4)^2}\) = \(\sqrt{9+16}\) = \(\sqrt{25}\) = 5 cm
∴ C.S.A. of cone = πrl
= \(\frac{22}{7}\) × 3 × 5 = \(\frac{330}{7}\) cm²
Radius of the hemisphere
\(\frac{d}{2}\) = \(\frac{6}{2}\) = 3 cm.
C.S.A. of the hemisphere = 2πr²
= 2 × \(\frac{22}{7}\) × 3 × 3 = \(\frac{396}{7}\)
Hence the surface area of the toy = C.S.A. of cone + C.S.A. of hemisphere
= \(\frac{330}{7}\) +\(\frac{396}{7}\)
= \(\frac{726}{7}\) = 103.71 cm²

Question 11.
If sec β + tan β = p, then express the value of sin β in terms of ‘p’.
Solution:
Given sec β + tan β = p ………….. (1)
sec² β – tan² β = 1
(sec β + tan β) (sec β – tan β) = 1
p(sec β – tan β) = 1
∴ sec β – tan β = \(\frac{1}{\mathrm{p}}\) ………….. (2)


Hence proved.

Question 12.
One card is drawn from a well-shuffled deck of 52 cards. Find the probability of getting
i) a king of red colour
ii) a face card
iii) a red face card
iv) the jack of hearts.
Solution:
Out of 52 cards one card can be drawn in 52 ways.
∴ The total number of outcomes n(S) = 52

i) Let E be the event ‘The card is a king of red colour”. ,
The no.of favourable outcomes n(E) = 2
∴ P(E) = \(\frac{\mathrm{n}(\mathrm{E})}{\mathrm{n}(\mathrm{S})}\) = \(\frac{2}{52}\) = \(\frac{1}{26}\)

ii) Let F be a event “The card is a face card”.
n(F) = 12
∴ P(E) = \(\frac{\mathrm{n}(\mathrm{F})}{\mathrm{n}(\mathrm{S})}\) = \(\frac{12}{52}\) = \(\frac{3}{13}\)

iii) Let G be a event The card is.a red face card”.
n(G) = 6
P(G) = \(\frac{\mathrm{n}(\mathrm{G})}{\mathrm{n}(\mathrm{S})}\) = \(\frac{6}{52}\) = \(\frac{3}{26}\)

iv) Let H be a event “The card is the jack of hearts”.
n(H) = 1
P(H) = \(\frac{\mathrm{n}(\mathrm{H})}{\mathrm{n}(\mathrm{S})}\) = \(\frac{1}{52}\)

Section – III (6 × 5 = 30 Marks)

Note :

1. Answer all the following questions.
2. In this section, every question has internal choice. Answer any one alternative.
3. Each question carries 5 marks.

Question 13.
A) Two men on either side of a temple of 30 meter height observe its top at the angles of elevation 30° and 60° respectively. Find the distance between the two men.
Solution:
Height of the temple BD = 30 meters
Angle of elevation of one person ∠DAB = 30°
Angle of elevation of another person ∠BCD = 60°
Let the distance between the first person and the temple, AD = x and distance between the second person and the temple, CD = d

From ΔBAD
tan 30° = \(\frac{\mathrm{BD}}{\mathrm{AB}}\)
\(\frac{1}{\sqrt{3}}=\frac{30}{x}\) ⇒ x = 30√3 …………. (1)
From ΔBCD
tan 60° = \(\frac{B D}{d}\)
√3 = \(\frac{30}{\mathrm{~d}}\)
d = \(\frac{30}{\sqrt{3}}\) ………….. (2)
From (1) and (2) distance between the persons
= BC + BA = x + d
= 30√3 + \(\frac{30}{\sqrt{3}}=\frac{30 \times 4}{\sqrt{3}}=\frac{120}{\sqrt{3}}\) = 40√3m
The required distance is 40√3 m.

(OR)

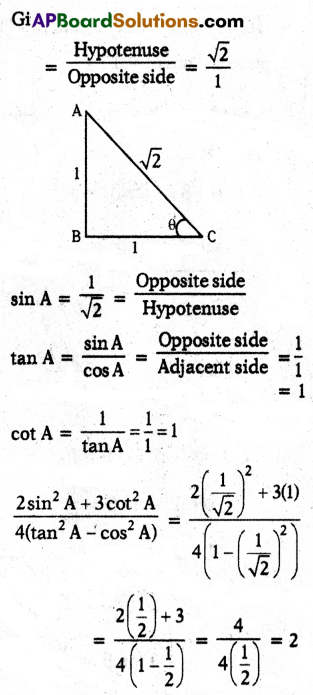
B) If cosec A = √2, then find the value of \(\frac{2 \sin ^2 A+3 \cot ^2 A}{4\left(\tan ^2 A-\cos ^2 A\right)}\).
Solution:
Given cosec A = √2

Question 14.
A) Prove that √3 + √5 is an irrational number.
Solution:
Let us suppose that -√3 + √5 is rational.

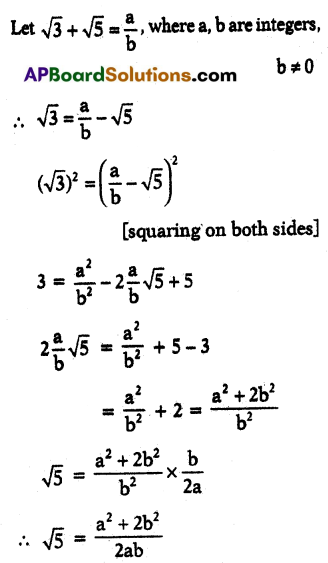
Since a, b are integers, \(\frac{a^2+2 b^2}{2 a b}\) is rational and so √5 is rational.
This contradicts the fact √5 is irrational.
Hence √3 + √5 is irrational.

(OR)

B) A right circular cylinder has base radius 14 cm and Height 21 on. Find its
i) Area of the base (area of each end)
ii) Curved surface area
iii) Total surface area iv) Volume
Solution:
Given that base radius of
cylinder r = 14 cm
Height h = 21 cm
i) Area of base = πr²
= π(14)²

Question 15.
A) The sum of the third and seventh terms of an AP is 6 and their product is 8. Find the sum of first sixteen terms of the AP.
Solution:
In an AP
3^rd term = a₃ = a + 2d
7^th term = a₇ = a + 6d
From given a₃ + a₇ = 6 and a₃ + a₇ = 8
Now take a₃ + a₇ = 6
a + 2d + a + 6d = 6
2a + 8d = 6
a + 4d = 3
a = 3 – 4d …………… (1)
Now take a₃ × a₇ = 8
(a + 2d) (a + 6d) = 8 …………… (2)
Substitute a = 3 – 4d in eqn. (2)
(3 – 4d + 2d) (3 – 4d + 6d) = 8
(3 – 2d) (3 + 2d) = 8
(3)² – (2d)² = 8
9 – 4d² = 8
9 – 8 = 4d²
4d² = 1 => d² = \(\frac{1}{4}\)
d = \(\frac{1}{2}\)
From (I) a = 3 – 4d
= 3 – 4 × \(\frac{1}{2}\) = 3 – 2 = 1
a = 1
Sum of 16 terms
= S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
S₁₆ = \(\frac{16}{2}\)[2 × 1 + (16 – 1) \(\frac{1}{2}\)]
= 8[\(\frac{2}{1}\) +\(\frac{15}{2}\)] = 8[latex]\frac{4+15}{2}[/latex]
= 4 × 19 = 76

(OR)

B) If the median of 60 observations, given below is 28.5 find the values of x and y.

Solution:

Class Interval	Frequency	c.f
0 – 10	5	5
10 – 20	x	5 + x
20 – 30	20	25 + x
30 – 40	15	40 + x
40 – 50	y	40 + x + y
50 – 60	5	45 + x + y

Median = l + (\(\frac{\left(\frac{n}{2}-c . f\right)}{f}\)) × h
It is given that Σf = n = 60
So, 45 + x + y = 60
x + y = 60 – 45 = 15
x + y= 15 ………….. (1)
The median is 28.5 which lies between 20 and 30.
∴ Median class = 20 – 30
Lower boundary of the median class ‘l’ = 20
\(\frac{N}{2}\) = \(\frac{60}{2}\) = 30
cf – cumulative frequency = 5 + x
h = 10
Median =l + (\(\frac{\left(\frac{n}{2}-c . f\right)}{f}\)) × h
⇒ 28.5 = 20 + \(\frac{30-5-x}{20}\) × 10
28.5 = 20 + \(\frac{25-x}{2}\)
\(\frac{25-x}{2}\) = 28.5 – 20 = 8.5
25 – x = 2 × 8.5
x = 25 – 17 = 8
also from (1); x + y = 15 8 + y = 15 ⇒ y = 7
∴ x = 8; y = 7.

Question 16.
A) From a pack of 52 playing cards, Jacks, Queens, Kings and Aces of red colour are removed. From the remaining, a card is drawn at random. Find the probability that the card drawn is (i) a black queen, (ii) a red card.
Solution:
Probability of black queen = \(\frac{1}{26}\)
Probability of red card = \(\frac{1}{2}\)
n(S) = 52
Probability of black queen n(a) = 2
p(a) = \(\frac{\mathrm{n}(\mathrm{a})}{\mathrm{n}(\mathrm{S})}\) = \(\frac{2}{52}\) = \(\frac{1}{26}\)
Probability of a red card n(b) = 26
p(b) = \(\frac{\mathrm{n}(\mathrm{b})}{\mathrm{n}(\mathrm{S})}\) = \(\frac{26}{52}\) = \(\frac{1}{2}\)

(OR)

B) If A = (x : x is a prime less than 20} and B = {x : x is a whole number less than 10},
then verify n(A∪B) = n(A) + n(B) – n(A∩B).
Solution:
Given
A = {x : x is a prime less than 20}
A = {2,3, .5, 7, 11,13, 17,19} n(A) = 8
B = {x: x is a whole number less than 10} = {0,1,2, 3,4, 5, 6, 7, 8, 9} n(B) = 10
n(A∪B) = n(A) + n(B) – n(A∩B) ………. (1)
A∩B = {2, 3, 5, 7, 11, 13, 17, 19} ∩ {0, 1,2, 3,4, 5, 6, 7, 8, 9}
= {2, 3, 5, 7}
n(A∩B) = 4
From (1) n (A∪B) = 8 + 10 – 4 = 14.

Question 17.
A) Draw the graph of p(x) = x² – 6x + 9 and find zeroes. Verify the zeroes of the polynomial.
Solution:
Given p(x) = x² – 6x + 9
Let y = x² – 6x + 9

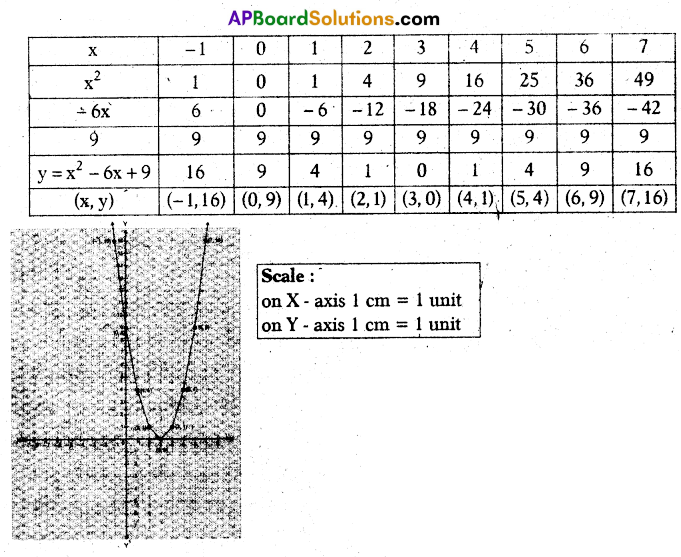
We observe that the graph touches the X – axis at (3, 0).
So, the zeroes of the given polynomial are equal.
∴ The zeroes of p(x) are 3, 3.
Justification:
Given p(x) = x² – 6x + 9 = 0
⇒ x² – 3x – 3x + 9 = 0
⇒ x(x – 3) – 3(x – 3) = 0
⇒ (x- 3) (x – 3) = 0
x – 3 = 0 (or) x – 3 – 0
x = 3 (or) x = 3
∴ Zeroes of p(x) = 3,3

(OR)

B) Solve the following pair of linear equations by graph method.
2x + y = 6 and 2x – y + 2 = 0.
Solution:
2x + y = 6

x	0	1	2	3
y	6	4	2	0
(x, Y)	(0, 6)	(1, 4)	(2, 2)	(3, 0)

2x – y + 2 =0

x	0	1	2
y	2	4	6
(x, y)	0, 2)	(1, 4)	(2, 6)

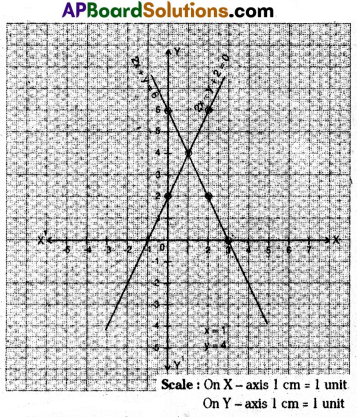
point of intersection is (1, 4)
∴ x = 1; y = 4

Question 18.
A) Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle 60°.
Solution:
Given that, ∠APB = 60°
Join OP.

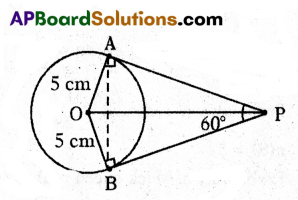
OP bisects ∠APB
∴ ∠OPA = ∠OPB = 30°

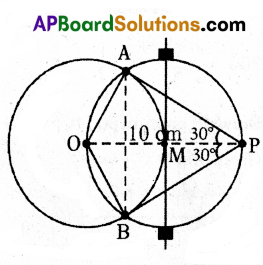
In ΔOAP sin 30° = \(\frac{\mathrm{OA}}{\mathrm{OP}}\) ⇒ \(\frac{1}{2}\) = \(\frac{5}{\mathrm{OP}}\)
∴ OP = 10 cm.
Now,

1. Draw a circle of radius 5 cm with centre ’O’.
2. Mark a point P at a distance of 10 cm from the centre of the circle.
3. Join OP and draw the perpendicular bisector of OP. Let it meet OP at M.
4. Taking M as centre and MO = MP as radius draw a circle. Which cuts the previous circle at A, B. Join PA and PB. Which are the required tangents.

(OR)

Construct a triangle PQR, in which PQ = 4 cm, QR = 6 cm and ∠PQR = 70°. Construct triangle such that each side of the new triangle is \(\frac{3}{4}\) of the triangle of PQR.
Solution:
Steps of construction :

• Draw a triangle PQR with given measurements.

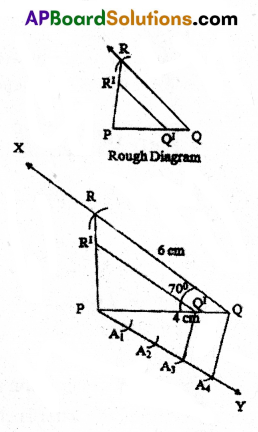
• Draw \(\overrightarrow{\mathrm{PY}}\) such that ∠QPY is an acute angle.
• Locate points A₁, A₂, A₃, A₄ on \(\overrightarrow{\mathrm{PY}}\) such that PA₁ = A₁ A₂ = A₂ A₃ = A₃ A₄.
• Join A₄ and Q.
• Draw a parallel line to A₄ Q through A₃ to meet PQ at Q¹.
• Draw a parallel line to QR through Q¹ to meet PR at R¹.
• ΔPQ¹ R¹ is required similar triangle.

Part – B (20 Marks)

Note :

1. Answer all the questions.
2. Each question carries 1 mark.
3. Answers are to ]be written in the Question paper only.
4. Marks will not be awarded in any case of over writing, rewriting or erased answers.

Note : Write the capital letters (A, B, C, D) showing the correct answer for the following questions in the brackets provided against them. (Marks : 20 × 1 = 20)

Question 1.
Which of the following is an irrational number ?
A) \(\frac{2}{3}\)
B) \(\sqrt{\left(\frac{16}{25}\right)}\)
C) √8
D) \(\sqrt{0.04}\)
Answer:
C) √8

Question 2.
The product of zeroes of the cubic polynomial 2x³ – 5x² – 14x + 8 is
A) -4
B) 4
C) -7
D) 25
Answer:
A) -4

Question 3.
A pair of linear equations which satisfies dependent system
A) 2x + y- 5 = 0; 3x – 2y – 4 = 0
B) 3x + 4y = 2 ; 6x + 8y = 4
C) x + 2y = 3 ; 2x + 4y = 5
D) x + 2y – 30 =t 0 ; 3x + 6y + 60 = 0
Answer:
B) 3x + 4y = 2 ; 6x + 8y = 4

Question 4.
The n^th term of AP is t_n = a + (n – 1)d, where ‘d’ represents
A) First term
B) Common difference
C) Common ratio
D) Radius
Answer:
B) Common difference

Question 5.
The number of two digit numbers which are divisible by 3
A) 30
B) 20
C) 29
D) 31
Answer:
A) 30

Question 6.
If A = {x: x is a letter in the word MATHEMATICS} and
B = {x: x is a letter in the word MISTEACH} then
A) A⊆ B
B) B ⊆ A
C) A = B
D) B = A
Answer:
B) B ⊆ A

Question 7.
The coordinates of the centre of the circle if the ends of the diameter are (2, -5) and (-2,9)
A) (0, 0)
B) (2, -2)
C) (-5, 9)
D) (0, 2)
Answer:
D) (0, 2)

Question 8.
The Discriminant of the Quadratic equation x² + x + 1 = 0 is
A) 2
B) -3
C) 3
D) -2
Answer:
B) -3

Question 9.
The lines l and m represents.

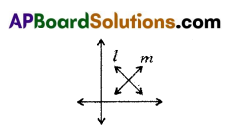
A) Inconsistent equation
B) Consistent equations
C) Dependent lines
D) Parallel lines
Answer:
B) Consistent equations

Question 10.
The slope of a ladder making an angle 30° with the floor is
A) 1
B) \(\frac{1}{\sqrt{3}}\)
C) √3
D) \(\frac{1}{2}\)
Answer:
B) \(\frac{1}{\sqrt{3}}\)

Question 11.
The distance between the points (cos α, 0), (0, sin α) is
A) 1
B) -1
C) 0
D) -2
Answer:
A) 1

Question 12.
The Arithmetic mean of 30 students is 42. Among them two got zero marks, then Arithmetic mean of remaining students.
A) 40
B) 42
C) 45
D) 28
Answer:
C) 45

Question 13.
The probability of getting king or queen card from the deck of cards
A) \(\frac{1}{52}\)
B) \(\frac{2}{13}\)
C) \(\frac{3}{26}\)
D) \(\frac{5}{52}\)
Answer:
B) \(\frac{2}{13}\)

Question 14.
Which of the following statement Is incorrect ?
A) The ratio of surface areas of cylinder and cone is 1 : 1
B) The ratio Surface Areas of sphere and hemisphere is 2 : 1
C) The ratio Total Surface Area of sphere and hemisphere is 2 : 1
D) The ratio of volumes of cylinder and cone is 3 : 1
Answer:
A) The ratio of surface areas of cylinder and cone is 1 : 1 & C) The ratio Total Surface Area of sphere and hemisphere is 2 : 1

Question 15.
The value of sin 30°+ cos60°is
A) 1
B) 0
C) -1
D) 2
Answer:
A) 1

Question 16.
At a particular time, if the angle of elevation of the sun is 45°, then the length of the shadow of a 5 m high tree is ……………… .
A) 5√3 m
B) 10 m
C) 5 m
D) \(\frac{5}{\sqrt{3}}\)m
Answer:
C) 5 m

Question 17.
When a dice is rolled, the probability of getting a composite number is [ ]
A) \(\frac{1}{4}\)
B) \(\frac{1}{2}\)
C) \(\frac{1}{3}\)
D) \(\frac{1}{6}\)
Answer:
C) \(\frac{1}{3}\)

Question 18.
The sum of first 100 natural numbers
A) 55
B) 505
C) 5050
D) 5500
Answer:
C) 5050

Question 19.
The sides PQ and PR of right angle triangle PQR are such that PQ = 5 cm, PR = 13 cm. If ∠Q = 90° then QR = ?
A) 11.2 cm
B) 9.6 cm
C) 12 cm
D) 10.2 cm
Answer:
C) 12 cm

Question 20.
If a quadrilateral ABCD is drawii to circumscribe a circle, then AB + CD is equal to !
A) AC + BD
B) AD + BC
C) AB + AD
D) AC + BD + BC
Answer:
B) AD + BC