TS 10th Class Maths Model Paper Set 2 with Solutions

The strategic use of TS 10th Class Maths Model Papers Set 2 can significantly enhance a student’s problem-solving skills.

TS SSC Maths Model Paper Set 2 with Solutions

Time: 3 Hours
Maximum Marks: 80

General Instructions:

1. Answer all the questions under Part – A on a separate answer book.
2. Write the answers to the questions under Part – B on the question paper itself and attach it to the answer book of Part – A.

Part – A (60 Marks)
Section – I (6 × 2 = 12 Marks)

Note :

1. Answer ALL the following questions.
2. Each question carries 2 marks.

Question 1.
Expand log a³b²c⁵.
Solution:
log a³b²c⁵ = log a³ + log b² + log c⁵
= 3 log a + 2 log b + 5 log c

Question 2.
If p(x) = x² + 3x + 4, then find the values of p(0) and p(1).
Solution:
p(x) = x² + 3x + 4
p(0) = (0)² + 3(0) + 4
= 0 + 0 + 4 = 4
∴ p(0) = 4
p(1) = (1)² + 3(1) + 4
= 1 + 3 + 4 = 8
∴ p(1) = 8

Question 3.
Find the 10^th term of the arithmetic progression 3, 5, 7, ……………
Solution:
3, 5, 7 ……………. A.P
a = 3, d = 2, n = 10
a_n = a + (n – 1)d
a₁₀ = 3 + (10 – 1)2
= 3 + (9 × 2)
= 3 + 18 = 21

Question 4.
Express tan θ in terms of sin θ.
Solution:
tan θ = \(\frac{\sin \theta}{\cos \theta}\)
sin² θ + cos² θ = 1
cos² θ = 1 – sin²θ
cos θ = \(\sqrt{1-\sin ^2 \theta}\)
∴ tan θ = \(\frac{\sin \theta}{\sqrt{1-\sin ^2 \theta}}\).

Question 5.
If a dice is rolled once, then find the probability of getting an odd number.
Solution:
Total outcomes = {1, 2, 3, 4, 5, 6)
Number of Total outcomes = 6
Favourable outcomes = {1, 3, 5}
Number of favourable outcomes = 3
P (an odd number)
= \(\frac{\text { Number of favourable outcomes }}{\text { Number of Total outcomes }}\)
= \(\frac{3}{6}\) = \(\frac{1}{2}\)

Question 6.
“The top of a tower is observed at an angle of elevation 45° and the foot of ‘ the tower is at a distance of 30 metres from the observer”. Draw a suitable diagram for this data.
Solution:

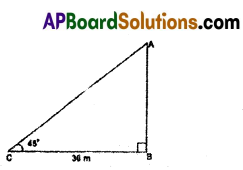
C – Point of observation
AB – Tower
A – Top of the tower

Section – II (6 × 3 = 18 Marks)

Note :

1. Answer ALL the following questions.
2. Each question carries 3 marks.

Question 7.
Solve : 2x + y = 5 and 5x + 3y = 11.
Solution:
2x + y = 5 ……………. (1)
5x + 3y = 11 …………… (2)

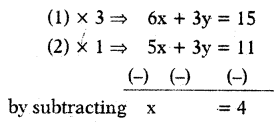
Substituting the value of x in equation (1)
⇒ 2(4) + y = 5
⇒ 8 + y = 5 ⇒ y = 5 – 8 ∴ y = -3
∴ x = 4, y = – 3 are the solution of the equations.

Question 8.
5, 8, 11, 14, ………. is an arithmetic progression. Find the sum of first 20 terms of it.
Solution:
5, 8, 11, 14, ……………. A.P
a = 5, d = 8 – 5 = 3, n = 20
S_n = \(\frac{n}{2}\)[2a + (n – 1) d]
S₂₀ = \(\frac{20}{2}\)[(2 × 5) + (20 – 1)3]
= 10[10 + 57]
= 10 × 67 = 670

Question 9.
Write a Quadratic equation, whose roots are 3 + √5 and 3 – √5 .
Solution:
Roots are 3 + √5 and 3 – √5 .
Sum of the roots = (3 + √5) + (3 – √5) = 6
Product of roots = (3 + √5) (3 – √5)
= 9 – 5 = 4
∴ Required Quadratic equation = x² – x (sum of the roots) + Product of roots = 0
∴ x² – 6x + 4 = 0

Question 10.
A box contains 20 cards which are numbered from 1 to 20. If one card is selected at random from the box, find the probability that it bears (i) a prime number, (ii) an even number.
Solution:
Total possibilities
= {1, 2, 3, 4, 5, 6, 7, 8, 9, ……………,20}
Number of Total possibilities = 20

i) Prime numbers
= {2, 3, 5, 7, 11, 13, 17, 19}
Number of favourable outcomes = 8
P(Prime Number)
= \(\frac{\text { Number of favourable outcomes }}{\text { Total number of outcomes }}\)
= \(\frac{8}{20}\) = \(\frac{2}{5}\)
∴ P(Prime Number) = \(\frac{2}{5}\)

ii) Even numbers
= {2,4, 6, 8, 10,12, 14, 16, 18,20}
Number of favourable outcomes = 10
P (Even Number)
\(\frac{\text { Number of favourable outcomes }}{\text { Total number of outcomes }}\)
= \(\frac{10}{20}\) = \(\frac{1}{2}\)
∴ P(Prime Number) = \(\frac{1}{2}\)

Question 11.
If two persons standing on either side of a tower of height 100 metres observes the top of it with angles of elevation of 60° and 45° respectively, then find the distance between the two persons.
[Note : Consider the two persons and the tower are on the same line.]
Solution:
Tower height = 100 m
Angles of elevation = 60° and 45°

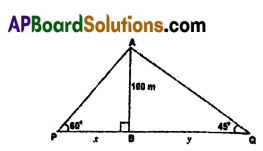
In ΔABP tan 60° = \(\frac{\mathrm{AB}}{\mathrm{PB}}\)
\(\frac{\sqrt{3}}{1}=\frac{100}{x}\)
√3 = x = 100 ⇒ x = \(\frac{100}{\sqrt{3}}\) m

In ΔABQ tan 45° = \(\frac{\mathrm{AB}}{\mathrm{BQ}}\)
\(\frac{1}{1}=\frac{100}{y}\) ⇒ y = 100 m
∴ The distance between Two persons = x + y
\(\frac{100}{\sqrt{3}}\) + 100 = \(\frac{100(\sqrt{3}+1)}{\sqrt{3}}\) m

Question 12.
In a trapezium ABCD, AB || DC. If diagonals intersect each other at point ‘O’, then show that \(\frac{\mathrm{AO}}{\mathrm{BO}}\) = \(\frac{\mathrm{CO}}{\mathrm{DO}}\)
Solution:
Given: In trapezium oABCD, AB // CD.
Diagonals AC, BD intersect at O.
R.T.P : \(\frac{\mathrm{AO}}{\mathrm{BO}}\) = \(\frac{\mathrm{CO}}{\mathrm{DO}}\)

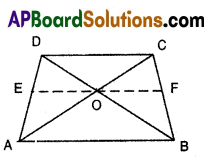
Construction : Draw a line EF passing through the point ‘O’ and parallel to CD and AB.
Proof: In ΔACD, EO//CD
∴ \(\frac{\mathrm{AO}}{\mathrm{CO}}\) = \(\frac{\mathrm{AE}}{\mathrm{DE}}\)
[∵ line drawn parallel to one side of a triangle divides other two sides in the same ratio by Basic proportionality theorem]
In ΔABD, EO //AB
Hence, \(\frac{\mathrm{DE}}{\mathrm{AE}}\) = \(\frac{\mathrm{DO}}{\mathrm{BO}}\)
[∵ Basic proportionality theorem]
\(\frac{\mathrm{BO}}{\mathrm{DO}}\) = \(\frac{\mathrm{AE}}{\mathrm{ED}}\) ………… (2)
From (1) and (2)
\(\frac{\mathrm{AO}}{\mathrm{CO}}\) = \(\frac{\mathrm{BO}}{\mathrm{DO}}\) [∵ Alternendo]

Section – III (6 × 5 = 30 Marks)

Note :

1. Answer all the following questions.
2. In this section every question has internal choice. Answer any one alternative.
3. Each question carries 5 marks.

Question 13.
A) If sec θ + tan θ = P, then prove that sin θ = \(\frac{\mathbf{P}^2-1}{\mathbf{P}^2+1}\)
Solution:
If sec θ + tan θ = P
Then sec θ – tan θ = \(\frac{1}{\mathrm{P}}\)
[∵ sec² θ – tan² θ = 1]
by adding (+) ⇒ 2 sec θ = P + \(\frac{1}{\mathrm{P}}\)
sec θ = \(\frac{\mathrm{P}^2+1}{2 \mathrm{P}}\) ……………… (1)

(OR)

B) Find the median for the following data.

Solution:

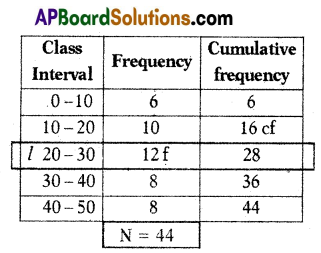
Median = l + (\(\frac{\frac{N}{2}-c f}{f}\)) × h
l = 20, \(\frac{N}{2}\) = \(\frac{44}{2}\) = 22, cf = 16
f = 12, h = 10
Median = 20 + (\(\frac{22-16}{12}\)) × 10
20 + (\(\frac{1}{12}\) × 10)
= 20 + (\(\frac{60}{12}\)) = 20 + 5 = 25
∴ Median =25

Question 14.
A) Prove that √5 + √7 Is an irrational number.
Solution:
Suppose √5 + √7 is not an irrational number.
√5 + √7 = \(\frac{p}{q}\) ; p, q ∈ Z, q ≠ 0
Squaring on both sides
(√5 + √7)² = (\(\frac{p}{q}\))²
⇒ 5 + 7 + 2\(\sqrt{35}\) = \(\frac{p^2}{q^2}\)
⇒ 2\(\sqrt{35}\) = \(\frac{p^2}{q^2}\) – 12
⇒ \(\sqrt{35}\) = \(\frac{p^2-12 q^2}{2 q^2}\)
[p² – 12q², 2q²∈ Z and 2q² ≠ 0]
∴ \(\frac{p^2-12 q^2}{2 q^2}\) is a rational number.
But \(\sqrt{35}\) is an irrational number.
An irrational number never be-comes equal to a rational number.
So our supposition that √5 + √7 is not an irrational number is false.
∴ √5 + √7 is an irrational number.

(OR)

B) The angle of elevation of the top of a hill from the foot of a tower is 60° and the angle of elevation of the top of the tower from the foot of the hill is 30°. If the tower is 50 m high. Find the height of the hill.
Solution:
Given height of the tower = AB = 50 m
Let height of hill be CD = h m
and distance between their feet be AC = x m
∠ACB = 30°, ∠CAD = 60°
From right angled Δ ABC, tan 30° = \(\frac{\mathrm{AB}}{\mathrm{AC}}\)

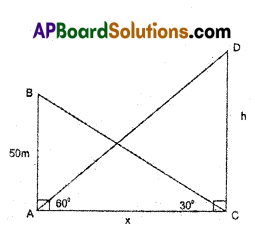
\(\frac{1}{3}\) = \(\frac{50}{x}\) ⇒ x = 50√3 m
From right angled Δ ACD, tan 60° = \(\frac{\mathrm{CD}}{\mathrm{AC}}\)
√3 = \(\frac{h}{x}\) ⇒ h = x√3 m
h = 50√3 .√3 (∵ x = 50√3m)
h = 50 × 3
⇒ h = 150 m.

Question 15.
A) Show that the distance of the points (5, 12), (7, 24) and (35, 12) from the origin are arranged in ascending order forms an arithmetic progression. Find the common difference of the progression.
Solution:
The distance of the point (x, y) from the origin = \(\sqrt{x^2+y^2}\)
The distance of the point (5, 12) from the origin = \(\sqrt{(5)^2+(12)^2}\) = \(\sqrt{25+144}\) = \(\sqrt{169}\) = 13 units;
The distance of the point (7, 24) from the origin = \(\sqrt{(7)^2+(24)^2}\) = \(\sqrt{49+576}\) = \(\sqrt{625}\) = 25 units.
The distance of the point (35, 12) from the origin = \(\sqrt{(35)^2+(12)^2}\) = \(\sqrt{1225+144}\) = \(\sqrt{1369}\) = 37 units.,
The ascending order of the distances is 13, 25, 37
a₁ a₂ a₃
a₂ – a₁ = 25 – 13 = 12
a₃ – a₂ = 37 – 25 = 12
a₂ – a₁ = a₃ – a₂
a₁, a₂, a₃ are in A.R
Common difference (d) = 12

(OR)

B)
The sum of the radius of base and height of a solid right circular cylinder is 37 cm. If it’s total surface area is 1628 square centimeters (cm²), then find the volume of the cylinder
(use π = \(\frac{22}{7}\))
Solution:

In the right circular cylinder
Let base radius = r
Height = h
r + h = 37 cm
Total surface area = 1628 sq.cm
Volume = ?
Total surface area of the cylinder = 2πr (r + h)
2πr(r + h) = 1628
2 × \(\frac{22}{7}\) × r × 37 = 1628
r = \(\frac{1628 \times 7}{2 \times 22 \times 37}\) = 7 cm
7 + h = 37 ⇒ h = 37 – 7 = 30 cm
∴ Volume = πr²h
= \(\frac{22}{7}\) × 7 × 7 × 30 = 4620 cm³

Question 16.
A) From the given Venn diagram, write the sets A∪B, A∩B, A – B and B – A.

Solution:
A = {1, 2, 3, 4, 5}, B = {2, 4, 6, 8}
A∪B = {1, 2, 3, 4, 5, 6, 8}
A∩B = (2, 4}
A- B = {1, 3, 5}
B – A = {6, 8}

(OR)

B) Sum of the areas of two squares is 850 m². If the difference of their perimeters is 40 m, find the sides of the two squares.
Solution:
Let the side of first square be ‘a’
the side of second square be ‘b’
Area of first square = ‘a²‘ m² ,
Area of second square = ‘b²‘ m²
Sum of the area of two squares = 850 m²
a² + b² = 850 ………… (1)
Perimeter of first square = ‘4a’m
Perimeter of second square = ‘4b’m
Difference of their perimeters = 40 m
4a – 4b = 40
a – b = 10 …………. (2)
a = b + 10
substitute this in eqn (1)
(b + 10)² + b² = 850
b² + 20b + 100 + b² = 850
2b² + 20b – 750 = 0
b² + 10b – 375 = 0
b² + 25b – 15b – 375 = 0
b(b + 25) – 15(b + 25) = 0
(b – 15) (b + 25) = 0
b = 15, b = – 25
from (2) a – 15 = 10 ⇒ a = 25
∴ The sides of two squares are 25m, 15m.

Question 17.
A) Draw the graph of the polynomial p(x) x² + 2x – 3 and find the zeroes of the polynomial from the graph.
Solution:
y = p(x) = x² + 2x – 3


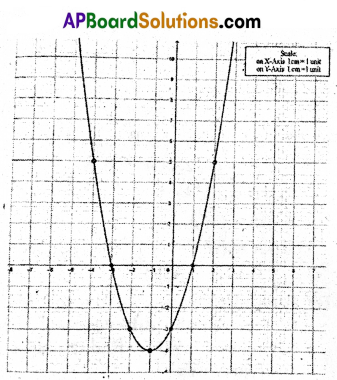
Zeros of the polynomial are – 3, 1

(OR)

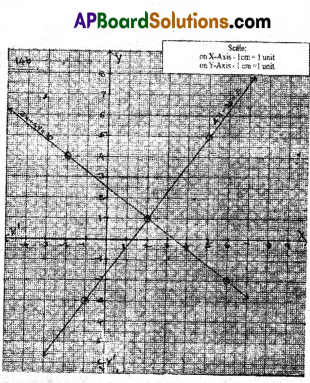
B) Solve the equations graphically 3x + 4y = 10 and 4x – 3y = 5.
Solution:
3x + 4y = 10 ……………… (1)

x	2	-2	6
y	1	4	-2
(x, y)	(2, 1)	(-2, 4)	(6, -2)

4x – 3y = 5. ……………… (2)

x	2	-1	5
y	1	-3	5
(x, y)	(2, 1)	(-1, -3)	(5, 5)

Intersecting point is (2, 1)
∴ x = 2, y = 1

Question 18.
A) Draw a circle of radius 4 cm. from a point 9 cm away from it’s centre, construct a pair of tangents to the circle.
Solution:

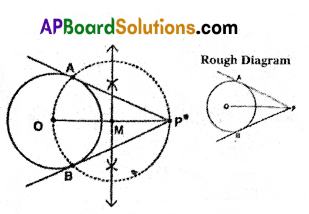
Steps of Construction :

1. Draw a circle of radius 4 cm.
2. Locate the point ‘P’ at a distance of 9 cm from the centre of the circle ‘O’ and join O, P.
3. Draw a perpendicular bisector for the line segment OP
4. Name the point of intersection of OP and its peipendicular bisector as M.
5. Consider M as centre and MO as the radius draw a circle.
6. Name the points of intersection of the two circles as A and B.
7. Draw PA and PB.
8. PA and PB are required tangents.

(OR)

B) Draw less than Ogive for the following frequency distribution. Find the median from obtained curve.

Solution:


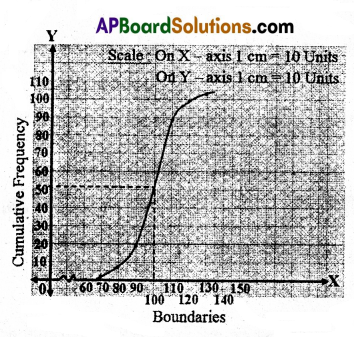
n = 103 ⇒ \(\frac{n}{2}\) = \(\frac{103}{2}\) = 51.5
Form graph, median = 100

Part – B (20 Marks)

Note :

1. Answer all the questions.
2. Each question carries 1 mark.
3. Answers are to be written in the Question paper only.
4. Marks will not be awarded in any case of over writing, rewriting or erased answers.

Note : Write the capital letters (A, B, C, D) showing the correct answer for the following questions in the brackets provided against them. (Marks; 20 × 1 = 20)

Question 1.
If A⊂B, then A∩B is …………….
A) A
B) B
C) μ
D) Φ
Answer:
A) A

Question 2.
The coefficient of x³ in the polynomial 2x⁴ – 5x³ + 6x² + 5 is ……………..
A) -5
B) 5
C) 6
D) 2
Answer:
A) -5

Question 3.
If the slope of the line joining the points (2, 5) and (x, 3) is 2, then the value of ‘x’ is ……………
A) 0
B) 1
C) -1
D) 2
Answer:
B) 1

Question 4.
The product of prime factors of 108 is ……………
A) 2³ × 3²
B) 2² × 3²
C) 2² × 3³
D) 2³ × 3³
Answer:
C) 2² × 3³

Question 5.
The number of solutions of the pair of linear equations
3x + 2y = 6 and 6x + 4y = 18 is ……………..
A) 0
B) 1
C) 2
D) infinite
Answer:
A) 0

Question 6.
“The total cost of 2 pens and 3 books is Rs. 110”.
Linear equation representing this data is ……………..
A) x + y = 110
B) 5x = 110
C) x² + y³ = 110
D) 2x + 3y = 110
Answer:
D) 2x + 3y = 110

Question 7.
If the n^th term of an arithmetic progression is 4n – 2, then its 10^th term is ……………..
A) 38
B) 28
C) 42
D) 24
Answer:
A) 38

Question 8.
If one root of the Quadratic equation x² – kx + 36 = 0 is 4, then the value of ‘k’ is ……………
A) 12
B) 17
C) 18
D) 13
Answer:
D) 13

Question 9.
The nature of roots of the Quadratic equation x² + 6x + 9 = 0 is …………………
A) Real and distinct.
B) Real and equal.
C) No real roots.
D) One is positive and the other is negative.
Answer:
B) Real and equal.

Question 10.
The sum of first 10 natural numbers is …………….
A) 45
B) 65
C) 55
D) 35
Answer:
C) 55

Question 11.
From the given Ogive curve, the value of the median of the data is ……………..

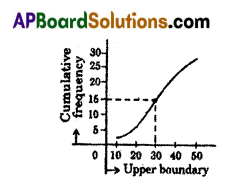
A) 20
B) 25
C) 15
D) 30
Answer:
D) 30

Question 12.
In the formula of volume of right circular cylinder V = πr²h, the letter ‘r’ represents ……………..
A) Diameter
B) Height
C) Volume
D) Radius
Answer:
D) Radius

Question 13.
If E and \(\overline{\mathbf{E}}\) are complementary events in a random experiment and P(\(\overline{\mathbf{E}}\)) = 0.3, the value of P(E) is ……………….
A) 0.3
B) 0.7
C) 1
D) 0
Answer:
B) 0.7

Question 14.
If one letter is selected randomly from the letters of the word “COVID”, then the probability of getting a vowel is ……………..
A) \(\frac{4}{5}\)
B) \(\frac{3}{5}\)
C) \(\frac{2}{5}\)
D) \(\frac{1}{5}\)
Answer:
C) \(\frac{2}{5}\)

Question 15.
ΔABC ~ ΔDEF, if ∠A = 45° and ∠E = 75°, then ∠C is ……………….
A) 90°
B) 120°
C) 30°
D) 60°
Answer:
D) 60°

Question 16.
ΔABC is a right triangle, right angled at B. If AB = 9 cm, BC = 12 cm, then AC is …………….
A) 13 cm
B) 14 cm
C) 15 cm
D) 16 cm
Answer:
C) 15 cm

Question 17.
In the given figure OA and OB are radii. PA and PB are tangents to the circle at points A and B. If ∠AOB = 130°, then ∠APB = ?

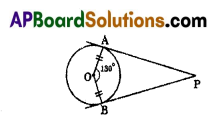
A) 40°
B) 50°
C) 60°
D) 70°
Answer:
B) 50°

Question 18.
If sin θ = \(\frac{3}{5}\), then the value of cos θ is (θ is acute angle) ……………..
A) \(\frac{1}{5}\)
B) \(\frac{5}{3}\)
C) \(\frac{4}{5}\)
D) \(\frac{2}{5}\)
Answer:
C) \(\frac{4}{5}\)

Question 19.
The maximum number of tangents can be drawn from an external point to a circle is ……………..
A) 1
B) 2
C) 3
D) 4
Answer:
B) 2

Question 20.
If θ is acute angle, then sin θ × sec θ = ……………….
A) tan θ
B) cot θ
C) 1
D) cosec θ
Answer:
A) tan θ