Inter 2nd Year

Use these Inter 2nd Year Maths 2A Formulas PDF Chapter 9 Probability to solve questions creatively.

Intermediate 2nd Year Maths 2A Probability Formulas

→ An experiment which can be repeated any number of times under essentially identical conditions and which is associated with a set of known results, is called a random experiment or trail if the result of any single repetition of the experiment ism certain and is any one of the associated set.

→ A combination of elementary events in a trial is called an event.

→ The list of all elementary events in a trail is called list of exhaustive events.

→ Elementary events are said to be equally likely if they have the same chance of happening.

→ If there are n exhaustive equally likely elementary events in a trail and m of them are
favourable to an event A, then \(\frac{m}{n}\) is called the probability of A. It is denoted by P(A).

→ P(A) = \(\frac{\text { Number of favourable cases (outcomes) with respect } A}{\text { Number of all cases (outcomes) of the experiment }}\)

→ The set of all possible outcomes (results) in a trail is called sample space for the trail. It is denoted by ‘S’. The elements of S are called sample points.

→ Let S be a sample space of a random experiment. Every subset of S is called an event.

→ Let S be a sample space. The event Φ is called impossible event and the event S is called certain event in S.

→ Two events A, B in a sample space S are said to be disjoint or mutually exclusive if A ∩ B = Φ

→ Two events A, B in a sample space S are said to be exhaustive if A ∪ B = S.

→ Two events A, B in a sample space S are said to be complementary if A ∪ B = S, A ∩ B = Φ. The complement B of A is denoted by Ā (or) A^c.

→ Let S be a finite sample space. A real valued function P: p(s) → R is said to be a probability function on S if (i) P(A) ≥ 0 ∀ A ∈ p(s) (ii) p(s) = 1

→ A, B, ∈ p(s), A ∩ B = Φ ⇒ P (A ∪ B) = P(A) + P(B). Then P is called probability function and for each A ∈ p(s), P(A) is called the probability of A.

→ If A is an event in a sample space S, then 0 ≤ P(A) ≤ 1.

→ If A is an event in a sample space S, then the ratio P(A) : P̄(Ā) is called the odds favour to A and P̄(A): P(A) is called the odds against to A.

→ If A, B are two events in a sample space S, then P(A ∪ B) = P(A) + P(B) – P(A ∩ B)

→ If A, B are two events in a sample space, then P(B – A) = P(B) – P(A ∩ B) and P(A – B) = P(A) – P(A ∩ B) .

→ If A, B, C are three events in a sample space S, then
P(A ∪ B ∪ C) = P(A) + P(B) + P(C) – P(A ∩ B) – P(B ∩ C) – P(C ∩ A) + P(A ∩ B ∩ C).

→ If A, B are two events in a sample space then the event of happening B after the event A happening is called conditional event It is denoted by B/A.

→ If A, B are two events in a sample space S and P(A) ≠ 0, then the probability of B after the event A has occured is called conditional probability of B given A. It is denoted by P\(\left(\frac{B}{A}\right)\)

→ If A, B are two events in a sample space S such that P(A) ≠ o then \(P\left(\frac{B}{A}\right)=\frac{n(A \cap B)}{n(A)}\)

→ Let A, B be two events in a sample space S such that P(A) ≠ 0, P(B) ≠ 0, then

• \(P\left(\frac{A}{B}\right)=\frac{P(A \cap B)}{P(B)}\)
• \(P\left(\frac{B}{A}\right)=\frac{P(A \cap B)}{P(A)}\)

→ Multiplication theorem on Probability: If A and B are two events of a sample space 5 and P(A) > 0, P(B) > 0 then P(A n B) = P(A), P(B/A) = P(B). P(A/B).

→ Two events A and B are said to be independent if P(A ∩ B) = P(A). P(B). Otherwise A, B are said to be dependent.

→ Bayes’ theorem : Suppose E₁, E₂ ……… E_n are mutually exclusive and exhaustive events of a Random experiment with P(E_i) > 0 for ī = 7, 2, ……… n in a random experiment then we have

\(p\left(\frac{E_{k}}{A}\right)\) = \(\frac{P\left(E_{k}\right) P\left(\frac{A}{E_{k}}\right)}{\sum_{i=1}^{n} P\left(E_{i}\right) P\left(\frac{A}{E_{i}}\right)}\) for k = 1, 2 …… n.

Random Experiment:
If the result of an experiment is not certain and is any one of the several possible outcomes, then the experiment is called Random experiment.

Sample space:
The set of all possible outcomes of an experiment is called the sample space whenever the experiment is conducted and is denoted by S.

Event:
Any subset of the sample space ‘S’ is called an Event.

Equally likely Events:
A set of events is said to be equally likely if there is no reason to expect one of them in preference to the others.

Exhaustive Events:
A set of events is said to be exhaustive of the performance of the experiment always results in the occurrence of at least one of them.

Mutually Exclusive Events:
A set of events is said to the mutually exclusive if happening of one of them prevents the happening of any of the remaining events.

Classical Definition of Probability:
If there are n mutually exclusive equally likely elementary events of an experiment and m of them are favourable to an event A then the probability of A denoted by P(A) is defined as min.

Axiomatic Approach to Probability:
Let S be finite sample space. A real valued function P from power set of S into R is called probability function if
P(A) ≥ 0 ∀ A ⊆ S
P(S) = 1, P(Φ) = 0;
(3) P(A ∪ B) = P(A) + P(B) if A ∩ B = Φ. Here the image of A w.r.t. P denoted by P(A) is called probability of A.

Note:

• P(A) + P(A̅) = 1
• If A₁ ⊆ A₂, then P(A₁) < P(A₂) where A₁, A₂ are any two events.

Odds in favour and odds against an Event:
Suppose A is any Event of an experiment. The odds in favour of Event A is P(A̅) : P(A). The odds against of A is P(A̅) : P(A).

Addition theorem on Probability:
If A, B are any two events in a sample space S, then P(A ∪ B) = P(A) + P(B) – P(A ∩ B).
If A and B are exclusive events

• P(A ∪ B) = P(A) + P(B)
• P(A ∪ B ∪ C) = P(A) + P(B) + P(C) – P(A ∩ B) P(A ∩ C) – P(B ∩ C) + P(A ∩ B ∩ C).

Conditional Probability:
If A and B are two events in sample space and P(A) ≠ 0. The probability of B after the event A has occurred is called the conditional probability of B given A and is denoted by P(B/A).
P(B/A) = \(\frac{\mathrm{n}(\mathrm{A} \cap \mathrm{B})}{\mathrm{n}(\mathrm{A})}=\frac{\mathrm{P}(\mathrm{A} \cap \mathrm{B})}{\mathrm{P}(\mathrm{A})}\)
Similarly
n(A ∩ B) = \(\frac{\mathrm{n}(\mathrm{A} \cap \mathrm{B})}{\mathrm{n}(\mathrm{B})}=\frac{\mathrm{P}(\mathrm{A} \cap \mathrm{B})}{\mathrm{P}(\mathrm{B})}\)

Independent Events:
The events A and B of an experiment are said to be independent if occurrence of A cannot influence the happening of the event B.
i.e. A, B are independent if P(A/B) = P(A) or P(B/A) = P(B).
i.e. P(A ∩ B) = P(A) . P(B).

Multiplication Theorem:
If A and B are any two events in S then
P(A ∩ B) = P(A) P(B/A) if P(A)≠ 0.
P (B) P(A/B) if P(B) ≠ 0.
The events A and B are independent if
P(A ∩ B) = P(A) P(B).
A set of events A₁, A₂, A₃ … A_n are said to be pair wise independent if
P(A_i n A_j) = P(A_i) P(A_j) for all i ≠ J.

Theorem:
Addition Theorem on Probability. If A, B are two events in a sample space S
Then P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
Proof:
FRom the figure (Venn diagram) it can be observed that
(B – A) ∪ (A ∩ B) = B, (B – A) ∩ (A ∩ B) = Φ

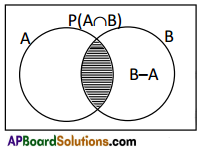
∴ P(B) = P[(B – A) ∪ (A ∩ B)]
= P(B – A) + P(A ∩ B)
⇒ P(B – A) = P(B) – P(A ∩ B) ………(1)

Again from the figure, it can be observed that
A ∪ (B – A) = A ∪ B, A ∩ (B – A) = Φ
∴ P(A ∪ B) = P[A ∪ (B – A)]
= P(A) + P(B – A)
= P(A) + P(B) – P(A ∩ B) since from (1)
∴ P(A ∪ B) = P(A) + P(B) – P(A ∩ B)

Theorem:
Multiplication Theorem on Probability.
Let A, B be two events in a sample space S such that P(A) ≠ 0, P(B) ≠ 0, then
i) P(A ∩ B) = P(A)P\(\left(\frac{B}{A}\right)\)
ii) P(A ∩ B) = P(B)P\(\left(\frac{A}{B}\right)\)
Proof:
Let S be the sample space associated with the random experiment. Let A, B be two events of S show that P(A) ≠ 0 and P(B) ≠ 0. Then by def. of confidential probability.
P\(\left(\frac{B}{A}\right)=\frac{P(B \cap A)}{P(A)}\)
∴ P(B ∩ A) = P(A)P\(\left(\frac{B}{A}\right)\)
Again, ∵P(B) ≠ 0
\(\left(\frac{\mathrm{A}}{\mathrm{B}}\right)=\frac{\mathrm{P}(\mathrm{A} \cap \mathrm{B})}{\mathrm{P}(\mathrm{B})}\)
∴ P(A ∩ B) = P(B) . P\(\left(\frac{\mathrm{A}}{\mathrm{B}}\right)\)
∴ P(A ∩ B) = P(A) . P\(\left(\frac{B}{A}\right)\) = P(B).P\(\left(\frac{\mathrm{A}}{\mathrm{B}}\right)\)

Baye’s Theorem or Inverse probability Theorem
Statement:
If A₁, A₂, … and A_n are ‘n’ mutually exclusive and exhaustive events of a random experiment associated with sample space S such that P(A_i) > 0 and E is any event which takes place in conjuction with any one of A_i then
P(A_k/E) = \(\frac{P\left(A_{k}\right) P\left(E / A_{k}\right)}{\sum_{i=1}^{n} P\left(A_{i}\right) P\left(E / A_{i}\right)}\), for any k = 1, 2, ………. n;
Proof:
Since A₁, A₂, … and A_n are mutually exclusive and exhaustive in sample space S, we have A_i ∩ A_j = for i ≠ j, 1 ≤ i, j ≤ n and A₁ ∪ A₂ ∪…. ∪ A_n = S.

Since E is any event which takes place in conjunction with any one of A_i, we have
E = (A₁ ∩ E) ∪ (A₂ ∩ E) ∪ …………….. ∪(A_n ∩ E).

We know that A₁, A₂, ……… A_n are mutually exclusive, their subsets (A₁ ∩ E), (A₂ ∩ E) , … are also
mutually exclusive.

Now P(E) = P(E ∩ A₁) + P(E ∩ A₂) + ………. + P(E ∩ A_n) (By axiom of additively)
= P(A₁)P(E/A₁) + P(A₂)P(E/A₂) + ………… + P(A_n)P(E/A_n)
(By multiplication theorem of probability)
= \(\sum_{i=1}^{n}\)P(A_i)P(E/A_i) …………..(1)

By definition of conditional probability
P(A_k/E) = \(\frac{P\left(A_{k} \cap E\right)}{P(E)}\) for
= \(\frac{P\left(A_{k}\right) P\left(E / A_{k}\right)}{P(E)}\)
(By multiplication theorem)
= \(\frac{P\left(A_{k}\right) P\left(E / A_{k}\right)}{\sum_{i=1}^{n} P\left(A_{I}\right) p\left(E / A_{i}\right)}\) from (1)
Hence the theorem

Use these Inter 2nd Year Maths 2A Formulas PDF Chapter 8 Measures of Dispersion to solve questions creatively.

Intermediate 2nd Year Maths 2A Measures of Dispersion Formulas

→ The arithmetic mean of ungrouped data = \(\frac{\Sigma x_{i}}{n}\) where n is the number of observations.

→ The median of ungrouped data
First expressing the n data points in the ascending order of magnitude.

→ If n is odd then \(\frac{n+1}{2}\)the data points in the median of the given ungrouped data.

→ If n is even then the average of \(\frac{n}{2}, \frac{n+2}{2}\) the data points in the median of the given ungrouped data.

• Range,
• Mean deviation,
• Variance and,
• Standard deviation are some measures of dispusion for ungrouped and grouped data.

→ Range is defined as the difference between the maximum value and the minimum value of the series of observations.

Mean Deviation for ungrouped distribution:
→ Mean deviation about the mean = \(\frac{\text { Sum of the absolutevalues of deviationsfrom } \bar{x}}{\text { Number of Observations }} .\)
= \(\frac{\sum\left|x_{i}-\bar{x}\right|}{n}\) where x̅ is the mean

→ Mean Deviation about the median = \(\frac{\sum\left|x_{i}-{median}\right|}{n}\)

Mean Deviation for grouped data:
→ Mean Deviation about mean = \(\frac{1}{N}\) Σf_i|x – x̅_i|
Where N = Σf_i and x̅ is the mean

→ Mean Deviation about median = \(\frac{1}{N}\) Σf_i|x_i – median|
When N = Σf_i

→ Ungrouped data variance σ² = \(\frac{1}{n}\) = Σ(x_i – x̅)²
Standard deviation σ = \(\sqrt{\frac{1}{n} \sum\left(x_{i}-\bar{x}\right)^{2}}\)

→ Discrete frequency distribution variance σ² = \(\frac{1}{n}\) = Σf_i(x_i – x̅)² where x̅ is the mean]
Standard deviation σ = \(\frac{1}{N}\) \(\sqrt{\sum f_{i}\left(x_{i}-\bar{x}\right)^{2}}\)

→ Continuous frequency distribution standard deviation σ = \(\frac{1}{N} \sqrt{N \sum f_{i} x_{i}{ }^{2}-\left(\sum f_{i} x_{i}\right)^{2}}\)
(or) σ = \(\frac{h}{N}\) \(\sqrt{N \Sigma f_{i} y_{i}^{2}-\left(\sum f_{i} y_{i}\right)^{2}}\)

→ Co-efficient of variation = \(\frac{\sigma}{x}\) × 100 (x̅ ≠ 0)

→ If each observation in a data is. multiplied by a constant K, then the variance of the resulting observations is K² times that or the variance of original observations.

→ If each of the observations x₁, x₂, ………, x_n is increased by K, where K is a positive or negative number then the variance remains unchanged.

Measure of Central Tendency:
1. Mathematical Average:
a) Arithmetic mean (A.M.)
b) Geometric mean (G.M.)
c) Harmonic mean (H.M.)

2. Averages of Position:
a) Median
b) Mode

Arithmetic Mean:
(1) Simple arithmetic mean in individual series
(i) Direct method: If the series in this case be x₁, x₂, …………. x_n then the arithmetic mean x̄ is given by
x̄ = \(\frac{\text { Sum of the series }}{\text { Number of terms }}\)
i.e x̄ = \(\frac{x_{1}+x_{2}+x_{3}+\ldots+x_{n}}{n}=\frac{1}{n} \sum_{i=1}^{n} x_{i}\)

(2) Simple arithmetic mean in continuous series If the terms of the given series be x₁, x₂, …………. x_n and the corresponding frequencies be f₁, f₂, …………. f_n then the arithmetic mean x̄ is given by,
x̄ = \(\frac{f_{1} x_{1}+f_{2} x_{2}+\ldots+f_{n} x_{n}}{f_{1}+f_{2}+\ldots+f_{n}}=\frac{\sum_{i=1}^{n} f_{i} x_{i}}{\sum_{i=1}^{n} f_{i}}\)

Continuous Series:
If the series is continuous then x_ii’s are to be replaced by m_i’s where m_i’s are the mid values of the class intervals.

Mean of the Composite Series:
If x̄_i,(i = 1, 2, …………… k) are the means of k-component series of sizes n_i(i = 1,2,….,k) respectively, then the mean x̄ of the composite series obtained on combining the component series is given by the formula x̄ = \(\frac{n_{1} \bar{x}_{1}+n_{2} \bar{x}_{2}+\ldots+n_{k} \bar{x}_{k}}{n_{1}+n_{2}+\ldots+n_{k}}=\frac{\sum_{i=1}^{n} n_{i} \bar{x}_{i}}{\sum_{i=1}^{n} n_{i}}\)

Geometric Mean:
If x₁, x₂, …………. x_n are n values of a variate x, none of them being zero, thengeometric mean (G.M.) is given by G.M. (x₁, x₂, …………. x_n)^1/n

In case of frequency distribution, G.M. of n values x₁, x₂, …………. x_n of a variate x occurring with frequency f₁, f₂, …………. f_n is given by G.M = (x₁^f₁, x₂^f₂, …………. x_n^f_n)^1/N, where N = f₁ + f₂ + ……….. + f_n

Continuous Series:
If the series is continuous then xjj’s are to be replaced by m_ii’s where m_ii’s are the mid values of the class intervals.

Harmonic Mean:
The harmonic mean of n items x₁, x₂, …………. x_n is defined as H.M. = \(\frac{n}{\frac{1}{x_{1}}+\frac{1}{x_{2}}+\ldots .+\frac{1}{x_{n}}}\)
If the frequency distribution is f₁, f₂, …………. f_n respectively, then H.M = \(\frac{f_{1}+f_{2}+f_{3}+\ldots . .+f_{n}}{\left(\frac{f_{1}}{x_{1}}+\frac{f_{2}}{x_{2}}+\ldots .+\frac{f_{n}}{x_{n}}\right)}\)

Median:
The median is the central value of the set of observations provided all the observations are arranged in the ascending or descending orders. It is generally used, when effect of extreme items is to be kept out.

(1) Calculation of median
(i) Individual series: If the data is raw, arrange in ascending or descending order. Let n be the number of observations.
If n is odd, Median = value of \(\left(\frac{n+1}{2}\right)^{t h}\) item.
If n is even, Median = \(\frac{1}{2}\)[value of \(\left(\frac{n}{2}\right)^{\text {th }}\) item + value of \(\left(\frac{n}{2}+1\right)^{\text {th }}\) item]

(ii) Discrete series: In this case, we first find the cumulative frequencies of the variables arranged in ascending or descending order and the median is given by
Median = \(\left(\frac{n+1}{2}\right)^{t h}\) observations, where n is the cumulative frequency.

(iii) For grouped or continuous distributions: In this case, following formula can be used.
(a) For series in ascending order, Median = l + \(\frac{\left(\frac{N}{2}-C\right)}{f}\) × i
Where l = Lower limit of the median class
f = Frequency of the median class
N = The sum of all frequencies
I = The width of the median class
C = The cumulative frequency of the class preceding to median class.

(b) For series in descending order
Median = u – \(\left(\frac{\frac{N}{2}-C}{f}\right)\) × i, where u = upper limit of the median class, N = \(\sum_{i=1}^{n}\)f_i
As median divides a distribution into two equal parts, similarly the quartiles, quintiles, deciles and percentiles divide the distribution respectively into 4, 5, 10 and 100 equal parts. The th quartile is given by Q = l + \(\left(\frac{j \frac{N}{4}-C}{f}\right)\)i:j= 1,2,3. Q₁ is the lower quartile, Q₂ is the median and Q₃ is called the upper quartile.

(2) Lower qualities

• Discrete series: Q₁ = size of \(\left(\frac{n+1}{4}\right)^{\text {th }}\) item
• Continuous series : Q₁ = l + \(\frac{\left(\frac{N}{4}-C\right)}{f}\) × i

(3) Upper qualities

• Discrete series : Q₃ = size of \(\left[\frac{3(n+1)}{4}\right]^{\text {th }}\) item
• Continuous series : Q₃ = l + \(\frac{\left(\frac{3N}{4}-C\right)}{f}\) × i

Mode:
The mode or model value of a distribution is that value of the variable for which the frequency is maximum. For continuous series, mode is calculated as,
Mode = l₁ + \(\left[\frac{f_{1}-f_{0}}{2 f_{1}-f_{0}-f_{2}}\right]\) × i
Where, l₁ = The lower limit of the model class
f₁ = The frequency of the model class
f₀ = The frequency of the class preceding the model class
f₂ = The frequency of the class succeeding the model class
i = The size of the model class.

Empirical relation :
Mean – Mode = 3(Mean – Median) ⇒ Mode = 3 Median – 2 Mean.

Measure of dispersion:
The degree to which numerical data tend to spread about an average value is called the dispersion of the data. The four measure of dispersion are

1. Range
2. Mean deviation
3. Standard deviation
4. Square deviation

(1) Range:
It is the difference between the values of extreme items in a series. Range = X_max – X_min

• The coefficient of range (scatter) = \(\frac{x_{\max }-x_{\min }}{x_{\max }+x_{\min }}\)
  Range is not the measure of central tendency. Range is widely used in statistical series relating to quality control in production.
• Range is commonly used measures of dispersion in case of changes in interest rates, exchange rate, share prices and like statistical information. It helps us to determine changes in the qualities of the goods produced in factories.

Quartile deviation or semi inter-quartile range:
It is one-half of the difference between the third quartile and first quartile i. e., Q.D. = \(\frac{Q_{3}-Q_{1}}{2}\) and coefficient of quartile deviation = \(\frac{Q_{3}-Q_{1}}{Q_{3}+Q_{1}}\), where Q₃ is the third or upper quartile and Q₁ is the lowest or first quartile.

(2) Mean Deviation:
The arithmetic average of the deviations (all taking positive) from the mean, median or mode is known as mean deviation.
Mean deviation is used for calculating dispersion of the series relating to economic and social inequalities. Dispersion in the distribution of income and wealth is measured in term of mean deviation.

• Mean deviation from ungrouped data (or individual series) Mean deviation = \(\frac{\sum|x-M|}{n}\) where |x – M| means the modulus of the deviation of the variate from the mean (mean, median or mode) and n is the number of terms.
• Mean deviation from continuous series: Here first of all we find the mean from which deviation is to be taken. Then we find the deviation dM =| x -M| of each variate from the mean M so obtained.
  • Next we multiply these deviations by the corresponding frequency and find the product f.dM and then the sum ΣfdM of these products.
  • Lastly we use the formula, mean deviation = \(\frac{\sum f|x-M|}{n}=\frac{\sum f d M}{n}\), where n = Σf.

(3) Standard Deviation:
Standard deviation (or S.D.) is the square root of the arithmetic mean of the square of deviations of various values from their arithmetic mean and is generally denoted by aread as sigma. It is used in statistical analysis.
(i) Coefficient of standard deviation: To compare the dispersion of two frequency distributions the relative measure of standard deviation is computed which is known as coefficient of standard deviation and is given by
Coefficient of S.D. = \(\frac{\sigma}{\bar{x}}\), where x̄ is the A.M.

(ii) Standard deviation from individual series σ = \(\sqrt{\frac{\sum(x-\bar{x})^{2}}{N}}\)
where, x̄ = The arithmetic mean of series
N = The total frequency.

(iii) Standard deviation from continuous series σ = \(\sqrt{\frac{\sum f_{i}\left(x_{i}-\bar{x}\right)^{2}}{N}}\)
where, x̄ = Arithmetic mean of series
x_i = Mid value of the class
f_i = Frequency of the corresponding
N = Σf = The total frequency

Short cut Method:
(i) σ = \(\sqrt{\frac{\sum f d^{2}}{N}-\left(\frac{\sum f d}{N}\right)^{2}}\)
(ii) σ = \(\sqrt{\frac{\sum d^{2}}{N}-\left(\frac{\sum d}{N}\right)^{2}}\)
where, d = x – A = Deviation from the assumed mean A
f = Frequency of the item
N = Σf = Sum of frequencies

(4) Square Deviation:
(i) Root mean square deviation
S = \(\sqrt{\frac{1}{N} \sum_{i=1}^{n} f_{i}\left(x_{i}-A\right)^{2}}\)
where A is any arbitrary number and S is called mean square deviation.

(ii) Relation between S.D. and root mean square deviation : If σ be the standard deviation and S be the root mean square deviation.
Then, S² = σ² + d².
Obviously, S² will be least when d = 0 i.e., x̄ = A
Hence, mean square deviation and consequently root mean square deviation is least, if the deviations are taken from the mean.

Variance:
The square of standard deviation is called the variance. Coefficient of standard deviation and variance : The coefficient of standard deviation is the ratio of the S.D. to A.M. i.e., \(\frac{\sigma}{x}\).
Coefficient of variance = coefficient of S.D.× 100 = \(\frac{\sigma}{x}\) × 100 .

Variance of the combined series :
If n₁,n₂ are the sizes, x̄₁, x̄₂ the means and σ₁, σ₂ the standard deviation of two series, then σ² = \(\frac{1}{n_{1}+n}\)[n₁(σ₁² + d₁²) + n₂(σ₂² + d₂²)]
where d₁ = x̄₁ – x̄, d₂ = x̄₂ – x̄ and x̄ = \(\frac{n_{1} \bar{x}_{1}+n_{2} \bar{x}_{2}}{n_{1}+n_{2}}\)

Use these Inter 2nd Year Maths 2A Formulas PDF Chapter 7 Partial Fractions to solve questions creatively.

Intermediate 2nd Year Maths 2A Partial Fractions Formulas

→ The quotient of two polynomials f(x) and Φ(x) where Φ(x) ≠ 0, is called a rational fraction.

→ If the degree of f(x) < the degree of Φ(x) in a rational fraction \(\frac{f(x)}{\phi(x)}\), then the rational fraction is called a proper fraction.

→ If the degree of f(x) ≥ the degree of Φ(x) in a rational fraction \(\frac{f(x)}{\phi(x)}\), then the rational fraction is called a proper fraction.

→ Let \(\frac{f(x)}{\phi(x)}\) be a proper fraction

→ When Φ(x) contains non-repeated linear factors only corresponding to every non-repeated linear factor (ax +b) of Φ(x) there exists a partial fraction of the form \(\frac{A}{a x+b}\) where A is a real number.

→ When Φ(x) contains repeated and non-repeated linear factors only corresponding to every repeated linear factor (ax + b)^p of Φ(x) there exist fractions of the form.
\(\frac{A_{1}}{a x+b}+\frac{A_{2}}{(a x+b)^{2}}+\ldots+\frac{A_{p}}{(a x+b)^{p}}\) Where A₁, A₂, A₃ ………… A_p are real numbers.

→ When Φ(x) contains non-repeated irreducible factors only. Corresponding to every non-repeated irreducible quadratic factor ax² + bx + c of Φ(x) of exists a partial fraction of the form \(\frac{A x+B}{a x^{2}+b x+C}\) where A and B are real numbers.

→ When Φ(x) contains repeated and non-repeated irreducible factors only. Corresponding to every repeated quadratic factor (ax² + bx + c0^p of Φ(x) there exists the partial fractions of the form
\(\frac{A_{1} x+B_{1}}{a x^{2}+b x+c}\) + \(\frac{A_{2} x+B_{2}}{\left(a x^{2}+b x+c\right)^{2}}\) + ……… + \(\frac{A_{p} x+\dot{B}_{p}}{\left(a x^{2}+b x+c\right)^{p}}\) where A₁, A₂, …….. A^p and B₁, B₂, ………. B_p are real numbers.

→ Let \(\frac{f(x)}{\phi(x)}\) be a improper fraction, then
\(\frac{f(x)}{\phi(x)}\) = Q(x) + \(\frac{R(x)}{\phi(x)}\) where Q(x) is quotient and R(x) is the remainder, and Degree R(x) < that of Φ(x).

→ Remainder obtained when f(x) is divided by x – a is f(a).
If degree of divisor is ‘n’, then the degree of remainder is (n – 1)
f(x), g(x) are two polynomials. If g(x) ≠ 0, then ∃ two polynomials q(x) , r(x) such that
\(\frac{f(x)}{g(x)}\) = q(x) + \(\frac{r(x)}{g(x)}\) if the degree of f(x) is > that of g(x)

II. Method of resolving proper fraction \(\frac{f(x)}{g(x)}\) into partial fractions.
Type 1 : When the denominator g(x) contains non-repeated factors i.e
g(x) = (x – a)(x – b)(x – c)
\(\frac{f(x)}{(x-a)(x-b)(x-c)}=\frac{\mathrm{A}}{\mathrm{x}-\mathrm{a}}+\frac{\mathrm{B}}{\mathrm{x}-\mathrm{b}}+\frac{\mathrm{C}}{\mathrm{x}-\mathrm{c}}\)

Type 2 : When the denominator g(x) contains repeated and non repeated linear factors
i.e g(x) = (x – a)²(x – b)
\(\frac{f(x)}{(x-a)^{2}(x-b)}=\frac{A}{x-a}+\frac{B}{(x-a)^{2}}+\frac{C}{(x-b)}\)

Type 3 : When the denominator g(x) contains non repeated irreducible quadratic factors
i.e g(x) = (ax² + bx + c)(x – d)

Type 4 : When the denominator g(x) contains repeated irreducible quadratic factors
i.e g(x) = (ax² + bx + c)²(x – d)
\(\frac{f(\mathrm{x})}{\left(\mathrm{ax}{ }^{2}+\mathrm{bx}+\mathrm{c}\right)^{2}(\mathrm{x}-\mathrm{d})}=\frac{\mathrm{Ax}+\mathrm{B}}{\left(\mathrm{ax}^{2}+\mathrm{bx}+\mathrm{c}\right)}+\frac{\mathrm{Cx}+\mathrm{D}}{\left(\mathrm{ax}^{2}+\mathrm{bx}+\mathrm{c}\right)^{2}}+\frac{\mathrm{E}}{\mathrm{x}-\mathrm{d}}\)

Use these Inter 2nd Year Maths 2A Formulas PDF Chapter 6 Binomial Theorem to solve questions creatively.

Intermediate 2nd Year Maths 2A Binomial Theorem Formulas

→ Let n be a positive integer and x, a be real numbers then
(x + a)ⁿ = ⁿC₀. xⁿ. a⁰ + ⁿC₁. x^{n – 1}. a¹ + ⁿC₂. x^{n – 2}. a² + ……… + ⁿC_r. x^{n – r}. a^r + ……… + ⁿC_n. x⁰. aⁿ = \(\sum_{r=0}^{n}\) ⁿC_r.x^{n – r}. a^r. and (x – a)ⁿ – ⁿC₀. xⁿ – (x)ⁿ – ⁿC₁. x^{n – 1}a + ⁿC₂ x^{n – 2}. a² …….. + ( – 1)^{r n}C_r. x^{n – r}. a^r + ……… + (- 1)^{n n}C_n.aⁿ

→ The expansion of (x + a)ⁿ contains (n + 1) terms.

→ In the expansion, the coefficients ⁿC₀, ⁿC₁, ⁿC₂, ….. ⁿC_n are called binomial coefficients and these are simply denoted by C₀, C₁, C₂, …….. C_n,.

→ In the expansion, (r + 1)^th term is called the general term. It is denoted by T_{r + 1}.
∴ T_{r + 1} = ^cC_r. x^{n – r}. a^r, (0 ≤ r ≤ n)

→ The number of terms in the expansion of (a + b + c)ⁿ = \(\frac{(n+1)(n+2)}{2}\)

→ If n is even in the expansion of (x + a)ⁿ, the middle term = T_{\(\left(\frac{n}{2}+1\right)\)}

→ If n is odd in the expansion of (x + a)ⁿ, it has two middle terms which are T_{\(\left(\frac{n+1}{2}\right)\)}, T_{\(\left(\frac{n+3}{2}\right)\)}.

→ If \(\frac{(n+1)|x|}{|x|+1}\) = p, a positive integer then p^th and (p + 1)^th terms are the numerically greatest terms in the expansion of (1 + x)ⁿ.

→ If \(\frac{(n+1)|x|}{|x|+1}\) = P + F where p is a positive integer and 0 < F < 1 then (p + 1)^th the numerically greatest term in the expansion of (1 + x)ⁿ

→ C₀ + C₁ + C₂ + ………. + C_n = 2ⁿ

→ C₀ – C₁ + C₂ – C₃ + ……… + (- 1)ⁿC_n = 0

→ C₀ + C₂ + C ₄ + …………… = C₁ + C₃ + C₅ + …………….. = 2^{n – 1}

→ \(\sum_{r=0}^{n}\) ⁿC_r = 2ⁿ

→ \(\sum_{r=0}^{n}\) r. ⁿC_r = n. 2^{n – 1}

→ \(\sum_{r=2}^{n}\) r(r – 1). ⁿC_r = n(n – 1). 2^{n – 2}

→ \(\sum_{r=1}^{n}\) r² . ⁿC_r = n(n + 1). 2^{n – 2}

→ a. C₀ + (a + d). C₁ + (a + 2d). C₂ + ……… + (a + nd). C_n = (2a + nd) 2^{n – 1}

→ C₀C_r + C₁C_{r + 1} + C₂C_{r + 2} + ………… + C_{n – r}. C_n = ²ⁿC_{n + r}

→ If f(x) = (a₀ + a₁x + a₂x² + ……… a_mx^m)ⁿ then

• Sum of the coefficients = f(1)
• Sum of the coefficients of even powers of x is \(\frac{f(1)+f(-1)}{2}\)
• Sum of the coefficients of odd powers of x is \(\frac{f(1)-f(-1)}{2}\)

→ Let n be a positive integer and x is a ,real number such that |x| < 1 then

→ (1 – x)^-n = 1 + nx + \(\frac{n(n+1)}{2 !}\) x² + \(\frac{n(n+1)(n+2)}{3 !}\) x² + ……… + ……… + \(\frac{n(n+1)(n+2) \ldots \ldots(n+r-1)}{r !}\) x^r + ……. to ∞

→ (1 + x)^-n = 1,- nx + \(\frac{n(n+1)}{2 !}\) x² + …….. + \(\frac{(-1)^{r} n(n+1)(n+2) \ldots(n+r-1)}{r !}\) x^r + …….. ∞

→ If |x| < 1, then for p, q ∈ N

→ (1 – x)^-p/q = 1 + \(\frac{p}{1 !}\left(\frac{x}{q}\right)\) + \(\frac{p(p+q)}{2 !}\left(\frac{x}{q}\right)^{2}\) + ………. + \(\frac{p(p+q) \ldots \ldots(p+(r-1) q)}{r !}\) \(\left(\frac{x}{q}\right)^{r}\) + …….. ∞

→ (1 + x)^-p/q = 1 – \(\frac{p}{1 !}\left(\frac{x}{q}\right)\) + \(\frac{p(p+q)}{2 !}\left(\frac{x}{q}\right)^{2}\) + ………. + \(\frac{(-1)^{r} p(p+q) \ldots(p+(r-1) q)}{r !}\) \(\left(\frac{x}{q}\right)^{r}\) + …….. ∞

→ (1 + x)^-p/q = 1 + \(\frac{p}{1 !}\left(\frac{x}{q}\right)\) + \(\frac{(p)(p-q)}{1 .2}\left(\frac{x}{q}\right)^{2}\) + …………. + \(\frac{(p)(p-q)(p-2 q) \ldots \ldots .[p-(r-1) q]}{(r) !}\) \(\left(\frac{x}{\cdot q}\right)^{r}\) + ……… ∞

→ (1 – x)^-p/q = 1 – \(\frac{p}{1 !}\left(\frac{x}{q}\right)\) + \(\frac{(p)(p-q)}{1.2}\left(\frac{x}{q}\right)^{2}\) – …………. + (- 1)^r \(\) \(\left(\frac{x}{q}\right)^{r}\) + ……… ∞

Binomial Theorem for integral index:
If n is a positive integer then (x + a)ⁿ = ⁿC_o xⁿ + ⁿC₁ x^n-1 a + ⁿC₂ x^n-2 a² + . … + ⁿC_r x^n-ra^r + …… + ⁿC_naⁿ

→ The expansion of (x + a)ⁿ contains (n + 1) terms.

→ In the expansion, the sum of the powers of x and a in each term is equal to n.

→ In the expansion, the coefficients ⁿC₀, ⁿC₁. ⁿC₂………….. ⁿC_n are called binomial coefficients and these are simply denoted by C₀, C₁, C₂ …. C_N.
ⁿC₀ = 1, ⁿC_N = 1, ⁿC₁ = n, ⁿC_r = ⁿC_n-r

→ In the expansion, (r + 1)^th term is called the general term. It is denoted by
T_r+1. Thus T_r+1 = ⁿC_rx_n-ra_r

→ (x + a)ⁿ = \(\sum_{r=0}^{n}\)ⁿC_rx_n-ra_r

→ (x + a)ⁿ = \(\sum_{r=0}^{n}\)ⁿC_rx_n-r(-a)_r = \(\sum_{r=0}^{n}\)(-1)^{n n}C_rx_n-r(-a)_r = ⁿC₀xⁿ – ⁿC₁x^n-1a + ⁿC₁x^n-2a² – ……….. + (-1)^{n n}C_n aⁿ

→ (1 + x)ⁿ = \(\sum_{r=0}^{n}\)ⁿC_rx_r = ⁿC₀ + ⁿC₀x + ……….. + ⁿC_n xⁿ = C₀ + C₁x + C₂x² + ………. + C_nxⁿ

→ Middle term(s) in the expansion of (x + a)ⁿ.

• If n is even, then (\(\frac{n}{2}\) + 1)th term is the middle term
• If n is odd, then \(\frac{n+1}{2}\) th and \(\frac{n+3}{2}\) th terms are the middle terms.

→ Numerically greatest term in the expansion of (1 + x)ⁿ :

• If \(\frac{(n+1)|x|}{|x|+1}\) = p, a integer then plu1 and (p + 1) th terms are the numerically greatest terms in the expansion of (1 + x).
• If \(\frac{(n+1)|x|}{|x|+1}\) = p + F where pis a positive integer and 0< F < 1 then (p+1) th term is the numerically greatest term in the expansion of (1 + x).

→ Binomial Theorem for rational index: If n is a rational number and
|x| < 1, then 1 + nx + \(\frac{n(n-1)}{2 !}\) x² + \(\frac{n(n-1)(n-2)}{3 !}\)x³ + ………… = (1 + x)ⁿ

→ If |x| < 1 then

• (1 + x)^-1= 1 – x + x² – x³ + … + (-1)^rx^r + …….
• (1 – x)^-1 = 1 + x + x² + x³ + … + x^r + …….
• (1 + x)^-2 = 1 – 2x + 3x² – 4x³ + … + (-1)^r (r + 1)x^r + ………..
• (1 – x)^-2 = 1 + 2x + 3x² + 4x³ + … +(r + 1)x^r + ….
• (1 – x)^-n = 1 – nx + \(\frac{n(n-1)}{2 !}\) x² – \(\frac{n(n-1)(n-2)}{3 !}\)x³ + …………..
• (1 – x)^-n = 1 + nx + \(\frac{n(n-1)}{2 !}\) x² + \(\frac{n(n-1)(n-2)}{3 !}\)x³ + ………

→ If |x| < 1 an dn is a positive integer, then

• (1 – x)^-n = 1 + ⁿC₁x + ⁽ⁿ⁺¹⁾C₂x² + ⁽ⁿ⁺²⁾C₃x³ + ………….
• (1 + x)^-n = 1 – ⁿC₁x + ⁽ⁿ⁺¹⁾C₂x² – ⁽ⁿ⁺²⁾C₃x³ + ………….

→ When |x| < 1
(1 – x)^-p/q = 1 + \(\frac{p}{1 !}\left(\frac{x}{q}\right)+\frac{p(p+q)}{2 !}\left(\frac{x}{q}\right)^{2}+\frac{p(p+q)(p+2 q)}{3 !}\left(\frac{x}{q}\right)^{3}\) + …………………∞

→ When |x| < 1
(1 + x)^-p/q = 1 – \(\frac{p}{1 !}\left(\frac{x}{q}\right)_{+} \frac{p(p+q)}{2 !}\left(\frac{x}{q}\right)^{2} \quad \frac{p(p+q)(p+2 q)}{3 !}\left(\frac{x}{q}\right)^{3}\) + …………………∞

Binomial Theorem:
Let n be a positive integer and x, a be real numbers, then (x + a)ⁿ = ⁿC₀.xⁿa° + ⁿC₁.xⁿa¹ + ⁿC₂.x^n-1a² + …………… + ⁿC_r.x^n-ra^r + ……….. + ⁿC_n.x⁰aⁿ
Proof :
We prove this theorem by u sing the principle of mathematical induction (on n).
When n = 1, (x + a)¹ =(x + a)¹ = x + a = ¹C₀x¹a°+ ¹C₁x°a¹
Thus the theorem is true for n = 1
Assume that the theorem is true for n = k ≥ 1 (where k is a positive integer). That is
(x+a)^k = ^kC₀x^k.a⁰ + ^kC₁x^k-2a² + ^kC₂.x^k-2a² + …+ ^kC_r.x^k-r.a^r + ………….. + ^kCx⁰a^k

Now we prove that the theorem is true when n = k + 1 also
(x + a)^k+1 = (x + a)(x + a)^k

Therefore the theorem is true for n = k + 1
Hence, by mathematical induction, it follows that the theorem is true of all positive integer n

Use these Inter 2nd Year Maths 2A Formulas PDF Chapter 5 Permutations and Combinations to solve questions creatively.

Intermediate 2nd Year Maths 2A Permutations and Combinations Formulas

→ Fundamental principle: If a work can be performed in m different ways and another work can be performed in n different ways, then the two works simultaneously can be performed in mn different ways.

→ If n is a non-negative integer then

• 0 ! = 1
• n ! = n (n – 1) ! if n > 0

→ The number of permutations of n dissimilar things taken ‘r at a time is denoted by ⁿP_r and ⁿP_r = \(\frac{n !}{(n-r) !}\) for 0 ≤ r ≤ n.

→ If n, r positive integers and r ≤ n, then

• ⁿP_r = n. ^{n – 1}P_{r – 1} if r ≥ 1
• ⁿP_r = n.(n – 1) ^{n – 2}P_{r – 2} if r ≥ 2
• ⁿP_r = ^{n – 1}P_r + r. ^{(n – 1)}P_{(r – 1)}

→ The number of injections that can be defined from set A into set B is ^n(B)p_n(A) n(A) ≤ n(B)

→ The number of bijections that can be defined from set A into set B having same number of elements with A is n(A)!

→ The number of permutations of1n’ dissimilar things taken ‘r’ at a time.

• Containing a particular thing is (r) ^{n – 1}P_{r – 1}
• Not containing a particular thing is ^{n – 1}P_r
• Containing a particular thing in a particular place is ^{n – 1}P_{r – i}.

→ The number of functions that can be defined from set A into set B in [n(B)]^n(A)

→ The sum of the r – digited numbers that can be formed using the given ‘n’ distinct non-zero digits (r ≤ n ≤ 9) is ^{(n – 1)}P_{(r – 1)} × sum of all n digits × 111 …… 1 (r times)

→ In the above, if ‘0’ is one among the given n digits, then the sum is ^{(n – 1)}P_{(r – 1)} × sum of the digits × 111 … 1 (r times) ^{(n – 2)}P_{(r – 2)} × sum of the digits × 111 … 1 [(r – 1) times]

→ The number of permutations of n dissimilar things taken r at a time when repetitions are allowed any number of times is n^r.

→ The number of circular permutations of n dissimilar things is (n – 1) !

→ In case of hanging type circular permutations like garlands of flowers, chains of beads etc., the number of circular permutations of n things is \(\frac{1}{2}\) [(n – 1) !]

→ If in the given n things, p alike things are of one kind, q alike things are of the second kind, r alike things are of the third kind and the rest are dissimilar, then the number of permutations (of these n things) is \(\frac{n !}{p ! q ! r !}\)

→ The number of combinations of n things taken r at a time is denoted by ⁿC_r and ⁿC_r = \(\frac{n !}{(n-r) ! r !}\) for 0 ≤ r ≤ n and \(\frac{{ }^{n} C_{r}}{{ }^{n} C_{r-1}}=\frac{n-r+1}{r}\) and ⁿP_r = r! ⁿC_r

→ If n, r are integers and 0 ≤ r ≤ n then ⁿc_r = ⁿC_{r – 1}

→ Let n, r, s are integers and 0 ≤ r ≤ n, 0 ≤ s ≤ n. If ⁿC_r = ⁿC_s then r = s or r + s = n.

→ The number of ways of dividing ‘m + n’ things (m ≠ n) into two groups containing m, n things is ^{(m + n)}C_m = ^{(m + n)}C_m = \(\frac{(m+n) !}{m ! n !}\)

→ The number of ways of dividing (m + n + p) things (m, n, p are distinct) into 3 groups of m, n, p things is \(\frac{(m+n+p) !}{m ! n ! p !}\).

→ The number of ways of dividing mn things into m equal groups is \(\frac{(m n) !}{(n !)^{m} m !}\)

→ The number of ways if distributing mn things equally to m persons is \(\frac{(m n) !}{(n !)^{m}}\)

→ If p alike things are of one kind, q alike things are of the second kind and r alike things are of the third kind, then the number of ways of selecting one or more things out of them is (p + 1) (q + 1) (r +1) – 1.

→ If m is a positive integer and m = p₁^α₁, p₁^α₂ …… p_k^α_k where p₁, p₂ …… p_k are distinct primes and α₁, α₂, …. α_k are non-negative integers, then the number of divisors of m is (α₁ + 1) (α₂ + 1) ……… (α_k + 1). [This includes 1 and m].

→ The total number of combinations of n different things taken any number of times is 2ⁿ.

→ The total number of combinations of n different things taken one or more at a timers 2ⁿ – 1.

→ The number of diagonals in a regular polygon of n sides is \(\frac{n(n-3)}{2}\)

→ Permutations are arrangements of things taken some or all at a time.

→ In a permutation, order of the things is taken into consideration.

→ ⁿp_r represents the number of permutations (without repetitions) of n dissimilar things taken r at a time.

→ Fundamental Principle: If an event is done in ‘m’ ways and another event is done in ‘n’ ways, then the two events can be together done in mn ways provided the events are independent.

→ ⁿp_r = \(\frac{n !}{(n-r) !}\) = n(n – 1)(n – 2) …………. (n – r + 1)

→ ⁿp₁ = n, ⁿp₂ = n(n-1), ⁿp₃ = n(n-1)(n-2).

→ ⁿp_r = n!

→ \(\frac{{ }^{\mathrm{n}} \mathrm{p}_{\mathrm{r}}}{{ }^{\mathrm{n}} \mathrm{p}_{\mathrm{r}-1}}\)ⁿp_n = n!

→ ⁿ⁺¹p_r = r. ⁿp_r-1 + ⁿp_r

→ ⁿp_r = r. ^n-1p_r-1 + ⁿp_r

→ ⁿp_r = r.^n-1p_r-1 + ^n-1p_r

→ The number of permutations of n things taken r at a time containing a particular thing is r × ^n-1p_r-1

→ The number of permutations of n things taken r at a time not containing a particular thing is ^n-1p_r

• The number of permutations of n things taken r at a time allowing repetitions is n^r.
• The number of permutations of n things taken not more than r at a time allowing repetitions is \(\frac{n\left(n^{\mathrm{r}}-1\right)}{(n-1)}\)

→ The number of permutations of n things of which p things are of one kind and q things are of another kind etc., is \(\frac{n !}{p ! q ! \ldots \ldots \cdots}\)

→ The sum of all possible numbers formed out of all the ‘n’ digits without zero is (n-1)! (sum of all the digits) (111 ……….. n times).

→ The sum of all possible numbers formed out of all the ‘n’ digits which includes zero is [(n -1)! (sum of all the digits) (111 …………… n times)] – [( n – 2)! (sum of all the digits)(111 ………….. (n -1) times]

→ The sum of all possible numbers formed by taking r digits from the given n digits which do not include zero is ^n-1p_r-1 (sum of all the digits)(111 …………… r times).

→ The sum of all possible numbers formed by taking r digits from the given n digits which include zero is ^n-1p_r-1(sum of all the digits)(111 ……………….. r times) – ^n-2p_r-2(sum of all the digits)(111 ……………….. (r-1) times).

• The number of permutations of n things when arranged round a circle is (n -1)!
• In case of necklace or garland number of circular permutations is \(\frac{(n-1) !}{2}\)

→ Number of permutations of n things taken r at a time in which there is at least one repetition is n^r – ⁿp_r.

→ The number of circular permutations of ‘n’ different things taken ‘r’ at a time is \(\frac{{ }^{n} \mathrm{P}_{\mathrm{r}}}{\mathrm{r}}\)

Use these Inter 2nd Year Maths 2A Formulas PDF Chapter 4 Theory of Equations to solve questions creatively.

Intermediate 2nd Year Maths 2A Theory of Equations Formulas

→ If n is a non-negative integer and a₀, a₁, a₂, ……….. a_n are real or complex numbers and a₀ ≠ 0, then the expression f(x) = a₀xⁿ + a₁x^{n – 1} + a₂x^{n – 2} + ……. + a_n is called a polynomial in x of degree n.

→ f(x) = a₀xⁿ + a₁x^{n – 1} + a₂x^{n – 2} + ……. + a_n = 0 is called a polynomial equation in x of degree n (a₀ ≠ 0). Every non-constant polynomial equation has atleast one root.

→ If f(α) = 0 then α is called a root of the equation f(x) = 0.

→ If f(α) = 0 then (x – α) is a factor of f(x).

Relation between roots and coefficients of an equation:
→ If α β γ are the roots of x³ + p₁x² + p₂x + p₃ = 0 then sum of the roots s₁ = α + β + γ = – p₁.
Sum of the products of two roots taken at a time s₂ = αβ + βγ + γα = p₂.
Product of all the roots, s₃ = αβγ = – p₃.

→ If α, β, γ, δ are the roots of x⁴ + p₁x³ + p₂x² + p₃x + p₄ = 0 then sum of the roots s₁ = α + β + γ + δ = – p₁.
Sum of the products of roots taken two at a time
s₂ = αβ + αγ + αδ + βγ + βδ + γδ = p₂.
Sum of the products of roots taken three at a time .
s₃ = αβγ + βγδ + γδα + δαβ = – p₃.
Product of the roots, s₄ = αβγδ = p₄.

→ For a cubic equation, when the roots are

• In A.P., then they are taken as a – d, a, a + d.
• In G.P., then they are taken as \(\frac{a}{r}\), a, ar.
• In H.P., then they are taken as \(\frac{1}{a-d}, \frac{1}{a^{\prime}}, \frac{1}{a+d}\).

→ For a bi quadratic equation, if the roots are

• In A.P., then they are taken as a – 3d, a – d, a + d, a + 3d.
• In C.P., then they are taken as \(\frac{1}{a-3 d}, \frac{1}{a-d}, \frac{1}{a+d}, \frac{1}{a+3 d}\).

→ In an equation with real coefficients, imaginary roots occur in conjugate pairs.

→ In an equation with rational coefficients, irrational roots occur in pairs of conjugate surds.

→ The equation whose roots are those of the equation f(x) = 0 with contrary signs is f(- x) = 0.

→ The equation whose roots are multiplied by kfa 0) of those of the proposed equation f(x) = 0 is f \(\left(\frac{x}{k}\right)\) = 0.

→ The equation whose roots are reciprocals of the roots of f(x) = 0 is f \(\left(\frac{1}{x}\right)\) = 0.

→ The equation whose roots are exceed by h than those of f(x) = 0 is f(x – h) = 0.

→ The equation whose roots are diminished by h than those of f(x) 0 is f(x + h) = 0.

→ The equation whose roots are the square of the roots of f(x) = 0 is obtained by eliminating square root from f(√x) = 0.

→ If f(x) = p₀xⁿ + p₁x^{n – 1} + p₂x^{n – 2} + ……. + p_n = 0 then to eliminate the second term,
f(x) = 0 can be transformed to f(x + h) = 0 where h = \(\frac{-p_{1}}{n \cdot p_{0}}\).

→ If an equation is unaltered by changing x into \(\frac{1}{x}\) then it is a reciprocal equation.

→ A reciprocal equation f(x) = p₀xⁿ + p₁x^{n – 1} + …… + pⁿ = 0 is said to be a reciprocal equation of first class p_i = p_{n – i} for all i.

→ A reciprocal equation f(x) = p₀xⁿ + p₁x^{n – 1} + …… + pⁿ = 0 is said to be a reciprocal equation of second class if p_i = – p_{n – i} for all i.

→ For an odd degree reciprocal equation of class one, – 1 is a root and for an odd degree reciprocal equation of class two, 1 is a root.

→ For an even degree reciprocal equation of class two, 1 and – 1 are roots.

→ If f(x) = 0 is an equation of degree ‘n’ then to eliminate r^th term, f(x) = 0 can be transformed to f(x + h) = 0 where h is a constant such that f^{(n – r + 1)}(h) = 0 i.e.,(n – r + 1)^th derivative of f(h) is zero.

→ Every n^th degree equation has exactly n roots real or imaginary.

→ Relation between, roots and coefficients of an equation.

(i) If α, β, γ are the roots of x³ + p₁x² + p₂x + p₃ = 0 the sum of the roots s₁ = α + β + γ = -p₁.
Sum of the products of two roots taken at a time s₂ = αβ + βγ + γα = -p₂
Product of all the roots, s₃ = αβγ= – p₃.

(ii) If α, β, γ, δ are the roots of x⁴ + p₁x³ + p₂x² + p₃x + p₄ = 0 then

• Sum of the roots s₁ = a+P+y+S = -p₁.
  s₂ = αβ + αγ + αδ + βα + βδ + γδ = p₂.
• Sum of the products of roots taken three at a time
  s₃ = αβγ + βγδ + γδα + δαβ = – p₃.
• Product of the roots, s₄ = αβγδ = p₄

→ For the equation xⁿ + p₁x^n-1 + p₂x^n-2 + ……… + p_n = 0

• Σ α₂ = p₁² – 2p₂
• Σ α₃ = -p₁³ + 3p₁p₂ – 3p₃
• Σ α₄ =p₁⁴ – 4p₁²p² + 2p₂² + 4p₁p₃ – 4p₄
• Σ α₂β = 3p₃ – p₁p₂
• Σ α₂βγ = p₁p₃ – 4p₄

Note: For the equation x³ + p₁x² + p₂x + p₃ = 0 Σα₂β₂ — p₂ -2p₁p₃

→ To remove the second term from a nth degree equation, the roots must be diminished by \(\frac{-\mathrm{a}_{1}}{\mathrm{na}_{0}}\) and the resultant equation will not contain the term with x^n-1.

→ If α₁ , α₂ ………………. , α_n are the roots of f(x) = 0, the equation

• Whose roots are \(\) is f\(\left(\frac{1}{x}\right)\) = 0
• Whose roots are kα₁, kα₂ …,kα_n is f\(\left(\frac{x}{h}\right)\) = 0
• Whose roots are α₁ – h, α₂ – h, …. α_n – h is f(x + h) = 0.
• Whose roots are α₁ + h, α₂ + h, ………….. α_n + h is f(x – h) = 0
• Whose roots are α₁², α₂²…. α₁² is f (f√y) = 0

→ In any equation with rational coefficients, irrational roots occur in conjugate pairs.

→ In any equation with real coefficients, complex roots occur in conjugate pairs.

→ If α is r – multiple root of f(x) = 0, then a is a (r – 1) – multiple root of f¹(x) = 0 and (r-2) – Multiple root of f ¹¹(x) = 0 and non multiple root of f^r-1(x) =0.

→ If f(x) = xⁿ + p₁x^n-1 + …………. + p_n-1x + p_n and f(a) and f(b) are of opposite sign, then at least
one real root of f(x) =0 lies between a and b.

(a) For a cubic equation, when the roots are

• In A.P., then they are taken as a – d, a, a + d
• In G.P., then are taken as \(\frac{a}{r}\), a, ar
• In H.P., then they are taken as \(\frac{1}{a-d}, \frac{1}{a}, \frac{1}{a+d}\)

(b) For a bi quadratic equation, if the roots are

• In A.P., then they are taken as a – 3d, a + d, a + 3d
• In G.P., then they are \(\frac{a}{d^{3}}, \frac{a}{d}\), ad, ad³
• In H.P., then they are taken as \(\frac{1}{a-3 d}, \frac{1}{a-d}, \frac{1}{a+d}, \frac{1}{a+3 d}\)

→ It an equation is unaltered by changing x into \(\frac{1}{x}\), then it is a reciprocal equation.

• A reciprocal equation f (x) = p₀xⁿ + p₁x^n-1 + ……………….. + p_n = 0 is said to be a reciprocal equation of first class p_i = p_n-i for all i.
• A reciprocal equation f (x) = p₀xⁿ + p₁x^n-1 + ……………….. + p_n = 0 = 0 is said to be a reciprocal equation of second class p_i = p_n-i for all i.
• For an odd degree reciprocal equation of class one, -1 is a root and for an odd degree reciprocal equation of class two, 1 is a root.
• For an even degree reciprocal equation of class two, 1 and -1 are roots.

→ If f(x) = 0 is an equation of degree ‘n’ then to eliminate rth term, .f(x) = 0 can be transformed to f(x+h) = 0 where h is a constant such that f^(n-r+1)(h) =0 i.e., (n – r + 1)^th derivative of f(h) is zero.

Use these Inter 2nd Year Maths 2A Formulas PDF Chapter 3 Quadratic Expressions to solve questions creatively.

Intermediate 2nd Year Maths 2A Quadratic Expressions Formulas

→ If a, b, c are real or complex numbers and a ≠ 0, then the expression ax² + bx + c is called a quadratic expression in the variable x.
Eg: 4x² – 2x + 3

→ If a, b, c are real or complex numbers and a ≠ 0, then ax² + bx + c = 0 is called a quadratic equation in x.
Eg: 2x² – 5x + 6 = 0

→ A complex number α is said to be a root or solution of the quadratic equation ax² + bx + c = 0 if aα² + bα + c = 0

→ The roots of ax² + bx + c = 0 are \(\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)

→ If α, β are roots of ax² + bx + c = 0, then α + β = \(\frac{-b}{a}\) and αβ = \(\frac{C}{a}\)

→ The equation of whose roots are α, β is x² – (α + β)x + αβ = 0

→ Nature of the roots: ∆ = b² – 4ac is called the discriminant of the quadratic equation ax² + bx + c = 0. Let α, β be the roots of the quadratic equation ax² + bx + c = 0
Case 1: If a, b, c are real numbers, then

• ∆ = 0 ⇔ α = β = \(\frac{-b}{2 a}\) (a repeated root or double root)
• ∆ > 0 ⇔ α and β are real and distinct.
• ∆ < 0, ⇔ α and β are non- real complex numbers conjugate to each other.

Case 2: If a, b, c are rational numbers, then

• ∆ = 0 ⇔ α and β are rational and equal (ei) α = \(\frac{-b}{2 a}\), a double root or a repeated root.
• ∆ > 0 and is a square of a rational number ⇔ α and β are rational and distinct.
• ∆ > 0 but not a square of a rational number ⇔ α and β are conjugate surds.
• ∆ < 0, ⇔ α and β are non- real ⇔ α and β are non-real con conjugate complex numbers.

→ Let a, b and c are rational numbers, α and β be the roots of the equations ax² + bx + c = 0. Then

• α, β are equal rational numbers if ∆ = 0.
• α, β are distinct rational numbers if ∆ is the square of a non zero rational numbers.
• α, β are conjugate surds if ∆ > 0 and ∆ is not the square of a nonzero square of a rational number.

→ If a₁x² + b₁x + c₁ = 0, a₂x² + b₂x + c₂ = 0 have two same roots, then \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)

→ If α, β are roots of ax² + bx + c = 0,

• the equation whose roots are \(\frac{1}{\alpha}, \frac{1}{\beta}\) is f \(\left(\frac{1}{x}\right)\) = 0. If c ≠ 0 (ie) αβ ≠ 0
• the equation whose roots are α + k, β + k is f(x – k) = 0
• the equation whose roots are kα and kβ is f\(\left(\frac{x}{k}\right)\) = 0
• the equation whose roots are equal but opposite in sign is f(-x) = 0
  (ie) the equation whose roots are – α, – β is f(-x) = 0.

→ If the roots of ax² + bx + c = 0 are complex roots then for x ∈ R, ax² + bx + c and ‘a’ have the same sign.

→ If α and β (α < β) are the roots of ax² + bx + c = 0 then

• ax² + bx + c and ‘a’ are of opposite sign when α < x < β
• ax² + bx + c and ‘a’ are of the same sign if x < α or x > β.

→ Let f(x) = ax² + bx + c be a quadratic function

• If a > 0 then f(x) has minimum value at x = \(\frac{-b}{2 a}\) and the minimum value is given by \(\frac{4 a c-b^{2}}{4 a}\)
• If a < 0 then f(x) has maximum value at x = \(\frac{-b}{2 a}\) and the maximum value is given by \(\frac{4 a c-b^{2}}{4 a}\)

→ A necessary and sufficient condition for the quadratic equation a₁x² + b₁x + c₁ = 0 and a₂x² + b₂x + c₂ = 0 to have a common root is (c₁a₂ – c₂a₁)² = (a₁b₂ – a₂b₁) (b₁c₂ – b₂c₁).

→ If a₁b₂ – a₂b₁ = 0 then common root of a₁x² + b₁x + c₁ = 0, a₂x² + b₂x + c₂ = 0 is \(\frac{c_{1} a_{2}-c_{2} a_{1}}{a_{1} b_{2}-a_{2} b_{1}}\).

→ The standard form of a quadratic ax² + bx + c = 0 where a, b, c ∈ R and a ≠ 0

→ The roots of ax² + bx + c = 0 are \(\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)

→ For the equation ax² + bx + c = 0, sum of the roots = \(-\frac{b}{a}\), product of the roots = \(\frac{c}{a}\).

→ If the roots of a quadratic are known, the equation is x² – (sum of the roots)x +(product of the roots)= 0

→ “Irrational roots” of a quadratic equation with “rational coefficients” occur in conjugate pairs. If p + √q is a root of ax² + bx + c = 0, then p – √q is also a root of the equation.

→ “Imaginary” or “Complex Roots” of a quadratic equation with “real coefficients” occur in conjugate pairs. If p + iq is a root of ax² + bx + c = 0. Then p – iq is also a root of the equation.

→ Nature of the roots of ax² + bx + c = 0

Nature of the Roots	Condition
Imagine	b2 – 4ac < 0
Equal	b2 – 4ac = 0
Real	b2 – 4ac ≥ 0
Real and different	b2 – 4ac > 0
Rational	b2 – 4ac is a perfect square a, b, c being rational
Equal in magnitude and opposite in sign	b = 0
Reciprocal to each other	c = a
Both positive	b has a sign opposite to that of a and c
Both negative	a, b, c all have same sign
Opposite sign	a, c are of opposite sign

→ Two equations a₁x² + b₁x + c₁ = 0, a₂x² + b₂x + c₂ = 0 have exactly the same roots if \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)

→ The equations a₁x² + b₁x + c₁ = 0, a2x² + b₂x + c₂ = 0 have a common root, if (c₁a₂ – c₂a₁)² = (a₁b₂ – a₂b₁)(b₁c₂ – b₂c₁) and the common root is \(\frac{c_{1} a_{2}-c_{2} a_{1}}{a_{1} b_{2}-a_{2} b_{1}}\) if a₁b₂ ≠ a₂b₁

→ If f(x) = 0 is a quadratic equation, then the equation whose roots are

• The reciprocals of the roots of f(x) = 0 is f\(\left(\frac{1}{x}\right)\) = 0
• The roots of f(x) = 0, each ‘increased’ by k is f(x – k) = 0
• The roots of f(x) = 0, each ‘diminished’ by k is f(x + k) = 0
• The roots of f(x) = 0 with sign changed is f(-x) = 0
• The roots of f(x) = 0 each multiplied by k(≠0) is f\(\left(\frac{x}{k}\right)\) = 0

→ Sign of the expression ax² + bx + c = 0

• The sign of the expression ax² + bx + c is same as that of ‘a’ for all values of x if b² – 4ac ≤ 0 i.e. if the roots of ax² + bx + c = 0 are imaginary or equal.
• If the roots of the equation ax² + bx + c = 0 are real and different i.e b² – 4ac > 0, the sign of the expression is same as that of ‘a’ if x does not lie between the two roots of the equation and opposite to that of ‘a’ if x lies between the roots of the equation.

→ The expression ax² + bx + c is positive for all real values of x if b² – 4ac < 0 and a > 0.

→ The expression ax² + bx + c has a maximum value when ‘a’ is negative and x = –\(\frac{\mathrm{b}}{2 \mathrm{a}}\). Maximum value of the expression = \(\frac{4 a c-b^{2}}{4 a}\)

→ The expression ax² + bx + c has a maximum value when ‘a’ is positive and x = –\(\frac{\mathrm{b}}{2 \mathrm{a}}\). Minimum value of the expression = \(\frac{4 a c-b^{2}}{4 a}\)

Theorem 1:
If the roots of ax² + bx + c = 0 are imaginary, then for x ∈ R , ax² + bx + c and a have the same sign.
Proof:
The root are imaginary
b² – 4ac < 0 4ac – b² > 0
\(\frac{a x^{2}+b x+c}{a}=x^{2}+\frac{b}{a} x+\frac{c}{a}=\left(x+\frac{b}{2 a}\right)^{2}+\frac{c}{a}-\frac{b^{2}}{4 a^{2}}=\left(x+\frac{b}{2 a}\right)^{2}+\frac{4 a c-b^{2}}{4 a^{2}}\)
∴ For x ∈ R, ax² + bx + c = 0 and a have the same sign.

Theorem 2.
If the roots of ax² + bx + c = 0 are real and equal to α = \(\frac{-b}{2 a}\), then α ≠ x ∈ R ax² + bx + c and a will have same sign.
Proof:
The roots of ax² + bx + c = 0 are real and equal
⇒ b² = 4ac ⇒ 4ac – b² = 0
\(\frac{a x^{2}+b x+c}{a}\) = x + \(\frac{b}{a}\)x + \(\frac{c}{a}\)
= \(\left(x+\frac{b}{2 a}\right)^{2}+\frac{c}{a}-\frac{b^{2}}{4 a^{2}}\)
= \(\left(x+\frac{b}{2 a}\right)^{2}+\frac{4 a c-b^{2}}{4 a^{2}}\)
= \(\left(x+\frac{b}{2 a}\right)^{2}\) > 0 for x ≠ \(\frac{-b}{2 a}\) = α
For α ≠ x ∈ R, ax² + bx + c and a have the same sign.

Theorem 3.
Let be the real roots of ax² + bx + c = 0 and α < β. Then
(i) x ∈ R, α < x< β ax² + bx + c and a have the opposite signs
(ii) x ∈ R, x < α or x> β ax² + bx + c and a have the same sign.
Proof:
α, β are the roots of ax² + bx + c = 0
Therefore, ax² + bx + c = a(x – α)(x – β)
\(\frac{a x^{2}+b x+c}{a}\) = (x – α)(x – β)

(i) Suppose x ∈ R, α < x < β
⇒ x < α < β then x – α < 0, x – β < 0 ⇒ (x – α)(x – β) > 0 ⇒ \(\frac{a x^{2}+b x+c}{a}\) > 0
⇒ ax² + bx + c, a have a same sign

(ii) Suppose x ∈ R, x > β, x > β > α then x – α > 0, x – β > 0
⇒ (x – α)(x – β) > 0 ⇒ \(\frac{a x^{2}+b x+c}{a}\) > 0
⇒ ax² + bx + c, a have same sign
∴ x ∈ R, x < α or x > β ⇒ ax² + bx + c and a have the same sign.

Use these Inter 2nd Year Maths 2A Formulas PDF Chapter 2 De Moivre’s Theorem to solve questions creatively.

Intermediate 2nd Year Maths 2A De Moivre’s Theorem Formulas

Statement:
→ If ‘n’ is an integer, then (cos θ + i sin θ)ⁿ = cos nθ + i sin nθ
If n’ is a rational number, then one of the values of
(cos θ + i sin θ)ⁿ is cos nθ + i sin nθ

n^th roots of unity:
→ n^th roots of unity are {1, ω, ω² …….. ω^{n – 1}}.
Where ω = \(\left[\cos \frac{2 k \pi}{n}+i \sin \frac{2 k \pi}{n}\right]\) k = 0, 1, 2 ……. (n – 1).
If ω is a n^th root of unity, then

• ωⁿ = 1
• 1 + ω + ω² + ………… + ω^{n – 1} = 0

Cube roots of unity:
→ 1, ω, ω² are cube roots of unity when

• ω³ = 1
• 1 + ω + ω² = 0
• ω = \(\frac{-1+i \sqrt{3}}{2}\), ω² = \(\frac{-1-i \sqrt{3}}{2}\)
• Fourth roots of unity roots are 1, – 1, i, – i

→ If Z₀ = r₀ cis θ₀ ≠ 0, then the n^th roots of Z₀ are α_k = (r₀)^1/n cis\(\left(\frac{2 k \pi+\theta_{0}}{n}\right)\) where k = 0, 1, 2, ……… (n – 1)

→ If n is any integer, (cos θ + i sin θ)ⁿ = cos nθ + i sin nθ

→ If n is any fraction, one of the values of (cosθ + i sinθ)ⁿ is cos nθ + i sin nθ.

→ (sinθ + i cosθ)ⁿ = cos(\(\frac{n \pi}{2}\) – nθ) + i sin(\(\frac{n \pi}{2}\) – nθ)

→ If x = cosθ + i sinθ, then x + \(\frac{1}{x}\) = 2 cosθ, x – \(\frac{1}{x}\) = 2i sinθ

→ xⁿ + \(\frac{1}{x^{n}}\) = 2cos nθ, xⁿ – \(\frac{1}{x^{n}}\) = 2i sin nθ

→ The nth roots of a complex number form a G.P. with common ratio cis\(\frac{2 \pi}{n}\) which is denoted by ω.

→ The points representing n^th roots of a complex number in the Argand diagram are concyclic.

→ The points representing n^th roots of a complex number in the Argand diagram form a regular polygon of n sides.

→ The points representing the cube roots of a complex number in the Argand diagram form an equilateral triangle.

→ The points representing the fourth roots of complex number in the Argand diagram form a square.

→ The nth roots of unity are 1, w, w²,………. , w^n-1 where w = cis\(\frac{2 \pi}{n}\)

→ The sum of the nth roots of unity is zero (or) the sum of the nth roots of any complex number is zero.

→ The cube roots of unity are 1, ω, ω² where ω = cis\(\frac{2 \pi}{3}\), ω² = cis\(\frac{4 \pi}{3}\) or
ω = \(\frac{-1+i \sqrt{3}}{2}\)
ω² = \(\frac{-1-i \sqrt{3}}{2}\)
1 + ω + ω² = 0
ω³ = 1

→ The product of the n^th roots of unity is (-1)^n-1 .

→ The product of the n^th roots of a complex number Z is Z(-1)^n-1 .

→ ω, ω² are the roots of the equation x² + x + 1 = 0

Use these Inter 2nd Year Maths 2A Formulas PDF Chapter 1 Complex Numbers to solve questions creatively.

Intermediate 2nd Year Maths 2A Complex Numbers Formulas

Definition of a complex number:
→ A number of the type z = x + yi, where x, y ∈ R and i = √- 1 i.e., i² = – 1 is called a complex number ‘x’ is called real part of z, and ‘y’ is called imaginary part of z. We write x = Re(z) and y = Im(z). A number z = x + yi is said to be purely real iff y = 0 (x ≠ 0) and purely imaginary iff x = 0 (y ≠ 0)
A complex number a + ib is an ordered pair of real numbers. It is denoted by (a, b), a ∈ R, b ∈ R.

→ Two complex numbers z₁ = (a, b), z₂ = (c, d) are said to be equal iff a = c and b = d.

→ If z₁ = (a, b), z₂ = (c, d) then

• z₁ + z₁ = (a + c, b + d)
• z₁ – z₂ = (a – c, b – d)
• z₁. Z₂ = (ac – bd, ad + bc) and
• \(\frac{z_{1}}{z_{2}}=\left(\frac{a c+b d}{c^{2}+d^{2}}, \frac{b c-a d}{c^{2}+d^{2}}\right)\)

Modulus and Amplitude:
→ The modulus of a complex number z = x + iy is defined as a non-negative real number r = \(\sqrt{x^{2}+y^{2}}\). It is denoted by |z|.

→ Any real number θ satisfying the equation cos θ = \(\frac{x}{r}\), sin θ = \(\frac{y}{r}\) is called an amplitude or argument of z. The unique argument θ of z satisfying – π < θ ≤ π is called the principal argument of z and is denoted by Arg z.

→ The polar form or modulus amplitude form of the complex number
z = x + iy is r(cos θ + i sin θ)

Conjugate of a complex number:
→ If z = x + iy i.e., x, y ∈ R, then the complex number x – iy is called conjugate of z and is written as z̅. The sum and product of a complex number and its Conjugate is always purely real.

Some properties of modulus, amplitude and conjugate:

• (z̅) = z
• z + z̅ = 2 Re (z) and z – z̅ = 2 Im (z)
• \(\overline{Z_{1} Z_{2}}\) = \(\overline{Z_{1}}\) \(\overline{Z_{2}}\)
• \(\) and \(\) (z₂ ≠ 0) and |z₁z₂| = |z₁| |z₂|
• zz̅ = |z|²
• |z| = |z̅|;
• |z₁ + z₂| ≤ |z₁| + |z₂|, |z₁ – z₂| ≤ |z₁| + |z₂|
• |z₁ – z₂| > | |z₁| – |z₂| |
  In (vii) and (viii) equality holds iff amp (z₁) – amp (z₂) is an integral multiple of 2π.
• amp (z₁ z₂) = amp (z₁) + amp (z₂) + nπ, for some n ∈ {- 1, 0, 1}
• amp \(\left(\frac{Z_{1}}{Z_{2}}\right)\) = amp (z₁) – amp (z₂) + nπ, for some n ∈ {- 1, 0, 1}
• \(\frac{1}{{cis} \alpha}\) = cis(- α)
• cis α cis β = cis (α + β)
• \(\frac{{cis} \alpha}{{cis} \beta}\) = cis (α – β)

De-Moivre’s theorem:

• If n is any integer, then (cos θ + i sin θ)ⁿ = cos nθ + i sin nθ
• If n = \(\frac{p}{q}\), where p and q are integers having no common factor and q > 1, then cos nθ + i sin nθ is one of the q values of (cos θ + i sin θ)ⁿ
• If z₀ = r₀ cis θ₀ ≠ 0, then the n^th roots of z₀ are α_k = r₀^1/n cis \(\left(\frac{2 k \pi+\theta_{0}}{n}\right)\),
  k = 0, 1, 2, 3 … (n-1)

Cube roots of unity:

• The cube roots of unity are 1, ω = \(\frac{-1+\sqrt{3 i}}{2}\) and ω² = \(\frac{-1-\sqrt{3 i}}{2}\)
• 1 + ω + ω² = 0 and w³ = 1; 1 + ω = – ω ², 1 + ω² = – ω, ω + ω² = – 1
• Either of the two non-real cube roots of unity is square of the other.
• For either of the two non – real cube roots a.and of unity α + β = – 1, αβ = – 1, α² = β, β² = α and α³ = β³ = 1
• (-1)^1/3 = – 1, – ω – ω²
• The n^th roots of unity are cis\(\left(\frac{2 k \pi}{n}\right)\), k = 0, 1, 2, ….. (n – 1)

Formulae:

→ Modulus of Z = \(\sqrt{x^{2}+y^{2}}\)

→ If \(\sqrt{a+i b}\) = (x + iy), then x = \(\sqrt{\frac{\sqrt{a^{2}+b^{2}}+a}{2}}\) and y = \(\sqrt{\frac{\sqrt{a^{2}+b^{2}}-a}{2}}\)

→ Conjugate of a + ib = a – ib

→ Conjugate of a – ib = a + ib

→ Any number of the form x + iy where x, y ∈ R and i² = -1 is called a Complex Number.

→ In the complex number x + iy, x is called the real part and y is called the imaginary part of the complex number.

→ A complex number is said to be purely imaginary if its real part is zero and is said to be purely real if its imaginary part is zero.
(a) Two complex numbers are said to be equal if their real parts are equal and their imaginary parts are equal.
(b) In the set of complex numbers, there is no meaning to the phrases one complex is greater than or less than another i.e. If two complex numbers are not equal, we say they are unequal.
(c) a+ ib > c + id is meaningful only when b = 0, d = 0.

→ Two complex numbers are conjugate if their sum and product are both real. They are of the form a + ib, a – ib.

→ cisθ₁ cisθ₂ = cis(θ₁ + θ₂), \(\frac{\operatorname{cis} \theta_{1}}{\operatorname{cis} \theta_{2}}\) = cis(θ₁ – θ₂), \(\frac{1}{\cos \theta+i \sin \theta}\) = cosθ – isinθ

→ \(\frac{a_{1}+i b_{1}}{a_{2}+i b_{2}}=\frac{\left(a_{1} a_{2}+b_{1} b_{2}\right)+i\left(a_{2} b_{1}-a_{1} b_{2}\right)}{a_{2}^{2}+b_{2}^{2}}\)

→ \(\frac{1+i}{1-i}\) = i, \(\frac{1-i}{1+i}\) = i

→ \(\sqrt{x^{2}+y^{2}}\) is called the modulus of the complex number x + iy and is denoted by r or |x + iy|

→ Any value of 0 obtained from the equations cos θ = \(\frac{x}{r}\), sin θ = \(\frac{y}{r}\) is called an amplitude of the complex number.

→ The amplitude lying between -π and π is called the principal amplitude of the complex number. Rule for choosing the principal amplitude.

→ If θ is the principal amplitude, then -π < 0 < π

→If α is the principle amplitude of a complex number, general amplitude = 2nπ + α where n ∈ Z.

• Amp (Z₁ Z₂) = Amp Z₁ + AmpZ₂
• Amp z + Amp z̅ = 2π (when z is a negative real number) = 0 (otherwise)

→ r(cos θ + i sin θ) is the modulus amplitude form of x + iy.

→ If the amplitude of a complex number is \(\frac{\pi}{2}\), its real part is zero.

→ If the amplitude of a complex number is \(\frac{\pi}{4}\), its real part is equal to its imaginary part.

Students can go through AP Inter 2nd Year Zoology Notes Lesson 5(a) Human Reproductive System will help students in revising the entire concepts quickly.

AP Inter 2nd Year Zoology Notes Lesson 5(a) Human Reproductive System

→ The sex organs of the Male Reproductive System in the pelvic region are a pair of testes, accessory ducts, glands and external genitalia.

→ Testes are suspended within a pouch called scrotum.

→ Scrotum maintains temperature of 2-2.5°C, necessary for spermatogenesis.

→ Scrotal sac is connected to abdominal cavity through ‘inguinal canal’.

→ Testis is held in position in the scrotum by the ‘gubernaculum’.

→ Testis is enclosed in a fibrous envelope called ‘tunica albuginea’.

→ A pouch of serous membrane ’tunica vaginalis’ covers testis.

→ Seminiferous tubules are present in the lobules of testis.

→ Spermatogonial mother cells of seminiferous tubules play an important role in spermatogenesis.

→ ‘Nourishing cells’ or ‘sertoli cells’ provide nutrition to spermatozoa.

→ Leydig cells produce ‘Testosterone’ hormone, that controls secondary sexual characters and spermatogenesis.

→ Epididymis is a storage organ of sperms and gives the sperms time to mature.

→ Urethra is the shared terminal duct of the reproductive arid urinary systems. It opens into penis through a opening called ‘urethral meatus’.

→ Penis is the copulatory organ of male and the enlarged, bulbous end of penis is called glans penis, and is covered by a foreskin or prepuce.

→ Seminal vesicles produce seminal fluid which contains nutrients for the nourishment of sperms.

→ Prostate gland’s secretion activates the spermotozoa and provides nutrition to them.

→ The secretion of bulbourethral glands acts as a flushing agent that washes out the acidic urinary residues that remain in urethra, before the semen is ejaculated.

→ The Female reproductive system consists of a pair of ovaries, a pair of oviducts, uterus, vagina and external genitalia.

→ Ovaries are enveloped by outer germinal epithelium and inner tunica albuginea.

→ The ovarian stroma is divided into an outer cortex and inner medulla. Cortex is more dense due to ovarian follicles and medulla is abundant with blood and lymphatic vessels and nerve fibres.

→ Fallopian tube is the site of fertilization which conducts ovum or zygote towards the uterus by peristalsis.

→ Uterus is a muscular pear-shaped structure and carries foetus, it is also known as womb.

→ Uterus opens into the vagina is called the cervix. The cavity of cervix is called cervical canal.

→ Bartholin’s glands lubricate vagina and are homologous to the bulbourethral glands of the male reproductive system.

→ Skene’s glands secrete a lubricating fluid when stimulated and are homologus to the prostate gland.

→ The nourishment of newborn baby is provided by milk produced from mother’s mammary glands.

→ Gametogenesis in. male is called Spermatogenesis and that in a female is called Oogenesis.

→ Spermatozoa is composed of head, neck middle piece and tail.

→ The cap like structure on the head of spermatozoa is called acrosome.

→ The middle piece of sperm contains mitochondria that produce energy for the movement of tail.

→ Ovum is produced from modified secondary follicle called Graafian follicle.

→ Ovum is sorrounded by a membrane called Zona Pellucida.

→ Corpus luteum secretes Progesterone for the maintenance of pregnancy.

→ The menstrual flow results due to breakdown of endometrial lining of the uterus and its blood vessels.

→ During follicular phase, primary follicles mature into Graafian follicles and produce gonadotropins LH & FSH.

→ Rupture of Graafian follicle by LH results in the release of ovum.

→ The enzyme hyaluronidase from acrosome of a sperm dissolves hyaluronic acid of the follicle cells thus making easy penetration of sperm into a ovum.

→ The nuclear union of sperm and ovum results in the formation of synkaryon or zygotic nucleus.

→ Implantation of blastocyte occurs on the 6th day of fertilization.

→ The extra embryonic or foetal membranes are chorion, amnion, allantois and yolk sac.

→ The sclerotome of enlbryo forms vertebral column.
The myotome fonns voluntary muscles.
The dermotome forms dermis of skin and other connective tissues.

→ The notochord and neural tube are formed by the converge and involution of chorda mesodermal cells through the Hensen’s node.

→ The placenta of human is called chorioallantoic placenta as allantois fuses with the chorion in the process of vascuralisation.

→ Placenta is deciduous, because during parturition placenta is Cast off causing extensive haemorrhage and there by bleeding.

→ Progesterone secreted by placenta is essential for the maintenance of preganancy after 4th month.

→ Human Chorionic Gonadotropin (HCG) presence is used as a test in the detection of pregnancy.

→ The gestation period in humans is 266 days or 38 weeks.

→ Most of the major organs are formed by the end of first trimester and by the end of nine months of pregnancy, the foetus is fully developed.

→ Oxytocin acts on the uterine muscle during parturition and causes stronger uterine contractions.

→ Mammary glands produce milk after the birth of pregnancy, called lactation.

→ Breast feeding is recommended by doctors for bringing up a healthy baby.

→ The primary aim of life is procreation (reproduction)

→ Sexual reproduction starts with formation and fusion of male and female gametes.

→ The process of formation of gametes is known as gametogenesis.

→ Fertilisation is the complete and permanent fusion of two gametes from parents to form a diploid zygote. This process is also called syngamy. [IPE]

→ The Testes produce sperms and male hormones (Testosterone) called androgens. [IPE]

→ The ovary produces ova and female hormones estrogen and progesterone. [IPE]

→ Human female sex organs present in the pelvic region are as follows: [IPE]

• Ovaries
• Fallopian tubes
• Uterus
• Vagina
• Vulva

→ Human male sex organs present in the pelvic region are as follows: [IPE]

1. Testes
2. Epididymis
3. Vasa deferentia
4. Urethra
5. Penis
6. Accessory glands

→ Seminal plasma in humans is rich in fructose, calcium [2009, 2010 PMT]

→ Sertoli cells are found in seminiferous tubules [2010 PMT]

→ The signal for parturition originate from placenta as well as fully dev eloped foetus. [2010, 12]

→ Menstrual flow occurs due to lack of progesterone. [NEET-2013]

→ The main function of mammalian corpus luteum is to produce progesterone. [NEET-2014]

→ Capacitation refers to changes in the sperm before fertilisation. [NEET-2015]

→ Hysterectomy is surgical removal of uterus [NEET-2015]

→ In human females, meiosis-II in the gamete is not completed until fertilisation. [NEET-2015]

→ Hormones like hCG, hPL, estrogen, progesterone are produced by placenta. [NEET-2016]

→ Capacitation occurs in female reproductive tract. [NEET-2017]

→ Colostrum, the yellowish fluid secreted by mother is very essential to impart immunity to the new bom infants because it contains Immunoglobulin A. [NEET-2019]

→ Receptors for sperm binding in mammals are present on zona peliucida. [NEET-2021]