AP Inter 2nd Year Physics Question Paper March 2020

Thoroughly analyzing AP Inter 2nd Year Physics Model Papers and AP Inter 2nd Year Physics Question Paper March 2020 helps students identify their strengths and weaknesses.

AP Inter 2nd Year Physics Question Paper March 2020

Time: 3 Hours
Maximum Marks: 60

Section – A (10 × 2 = 20 Marks)

Note :

• Answer ALL questions.
• Each question carries TWO marks.
• ALL are very short answer type questions.

Question 1.
Two lenses of power -1.75 D and + 2.25 D respectively, are placed in contact. Calculate the focal length of the combination.
Solution:
P₁ = -1.75 D, P₂ = + 2.25 D.
P = P₁ + P₂
P = -1.75 + 2.25
P = 0.5
\(\frac{1}{F}\) = P
F = \(\frac{1}{\mathrm{P}}\) = \(\frac{1}{0.5}\) = 2m
F = 200 cm

Question 2.
What is the importance of Oersted’s experiment ?
Answer:
Importance of Oersted’s experiment is every current carrying conductor produces a magnetic field around it and which is perpendicular to current carrying conductor.

Question 3.
Classify the following materials with regard to magnetism : Manganese, Cobalt, Nickel, Bismuth, Oxygen, Copper.
Answer:
Ferromagnetic materials → Cobalt, Nickel
Paramagnetic materials → Oxygen, Manganese
Diamagnetic materials → Bismuth, Copper

Question 4.
Define magnetic inclination or angle of dip.
Answer:
Inclination or Dip (I) : The angle which the total intensity of earth’s magnetic field makes with the horizontal at any place is called inclination (I).

Question 5.
What is transformer ratio ?
Answer:
The ratio of secondary e.m.f to the primary e.m.f. (or) number of turns in secondary to the number of turns in the primary is called the transformer ratio.
Transformer ratio = \(\frac{V_s}{V_p}=\frac{N_s}{N_p}\)

Question 6.
The charging current for a capacitor is 0.6 A. What is the dis-placement current across its plates ?
Answer:
i = charging current for a capacitor = 0.6 A
i – i_d – ε₀ \(\frac{\mathrm{d} \phi_{\mathrm{B}}}{\mathrm{dt}}\)
∴ i = i_d = 0.6 A
∴ Displacement current (i_d) = 0.6 A.

Question 7.
What is “Photoelectric effect” ?
Answer:
When light of sufficient energy is incident on the photometal surface, electrons are emitted. This phenomenon is called photoelectric effect.

Question 8.
What is the de Broglie wavelength associated with an electron, accelerated through a potential difference of 100 volts ?
Solution:
Accelerating potential V = 100V. The de Broglie wavelength λ is 1.227
λ = h/p = \(\frac{1.227}{\sqrt{v}}\) nm
λ = \(\frac{1.227}{\sqrt{100}}\) nm = 0.123 nm
The de Broglie wavelength associated with an electron in this case is of the order of X-ray wavelengths.

Question 9.
In which bias can a zener diode be used as voltage regulator ?
Answer:
In reverse bias Zener diode can be used as voltage regulator.

Question 10.
Mention the frequency range of speech signals.
Answer:
Speech signals frequency range is 300 Hz to 3100 Hz.

Section – B (6 × 4 = 24 Marks)

Note :

• Answer ANY SIX questions.
• Each question carries FOUR marks.
• ALL are short answer type questions.

Question 11.
Explain the formation of rainbow.
Answer:

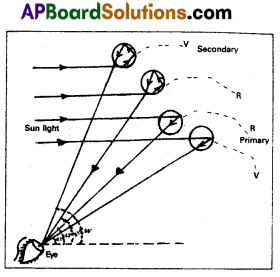
Figure shows how sun light is broken into its segments in the process and a rainbow appears. The dispersion of the violet and the red rays after internal reflection in the drop is shown in figure.

The red rays emerge from the drops of water at one angle (43°) and the violet rays emerge at another angle (41°). The large number of water drops in the sky makes a rainbow. The rainbow appears semicircular for an observer on earth.

Question 12.
Does the principle of conservation of energy hold for interference and diffraction phenomena ? Explain briefly.
Answer:
Yes, law of conservation of energy is obeyed. Incase of constructive interference, intensity becomes maximum. Hence, bright fringes are formed on the screen where as in the case of destructive interference, intensity becomes minimum. Hence, dark fringes are formed on the screen.

This establishes that in the interference and diffraction pattern, the intensity of light is simply being redistributed i.e., energy is being transferred from dark fringe to bright fringe. No energy is being created (or) destroyed in the process. Hence, energy is redistributed.

Thus, the principle of conservation of energy is being obeyed in the process of interference and diffraction.

Question 13.
State Gauss’s law in electrostatics and explan its importance.
Answer:
Gauss’s law : The total electric flux through any closed surface is equal to \(\frac{1}{\varepsilon_0}\) times the net charge enclosed by the surface.
Total electric flux, Φ \(\oint_s \vec{E} \cdot d \vec{s}=\frac{q}{\varepsilon_0}\)
Here, q is the total charge enclosed by the surface ‘S’. \(\oint\) represents surface integral of the closed surface.

Importance :

1. Gauss’s law is very useful in calculating the electric field incase of problems where it is possible to construct a closed surface. Such surface is called Gaussian surface.
2. Gauss’s law is true for any closed surface, no matter what its shape or size.
3. Symmetric considerations in many problems make the appli-cation of Gauss’s law much easier.

Question 14.
Derive an expression for the capacitance of a parallel plate capacitor.
Answer:

• P and Q are two parallel plates of a capacitor separated by a distance of d.
• The area of each plate is A. The plate P is charged and Q is earth connected.
• The charge on P is + q and surface charge density of charge = σ
  ∴ q = Aσ
• The electric intensity at point x, E = \(\frac{|\sigma|}{\varepsilon_0}\)
• Potential difference between the plates P and Q,

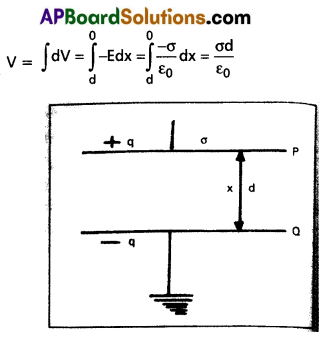
• Capacitance of the capacitor C = \(\frac{\mathrm{Q}}{\mathrm{V}}\) = \(\frac{A \sigma}{\frac{\sigma d}{\varepsilon_0}}\) = \(\frac{\varepsilon_0 A}{d}\) Farads (In air)
  Note : Capacity of a capacitor with dielectric medium is C = \(\frac{\varepsilon_0 A}{\left[d-t+\frac{t}{k}\right]}\) Farads.

Question 15.
State and explain Ampere’s law.
Answer:
Ampere’s law : The lineintegral of the intensity of magnetic induction field around closed path is equal to µ₀ times the net current (i) enclosed by the path.
\(\oint \overrightarrow{\mathbf{B}} \cdot \overrightarrow{\mathrm{d}} l\) = µ₀i

Proof : Consider a long straight conductor carrying current i as shown in figure. Magnetic induction at a distance r from the conductor is given by
B = \(\frac{\mu_0 i}{2 \pi r}\) s(From Biot-Savart’s law)
The value of B is same at all points on the circle.
\(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{d}} l=\oint \mathrm{B} d \cos \theta\)
= \(\mathrm{B} \oint \mathrm{d} l\) = B × 2πr (∵ = 0 Angle betv.een is zero)
= \(\frac{\mu_0 \mathrm{i}}{2 \pi \mathrm{r}}\) × 2πr
\(\oint \overrightarrow{\mathrm{B}} \& \overrightarrow{\mathrm{d} l}\) = µ₀i

Question 16.
Obtain an expression for the mutual inductance of two long co-axial solenoids.
Answer:
Consider two solenoids as shown in figure. The length of primary coil be l and are a of cross section A. Let N₁ and N₂ are the total number of turns in the primary and secondary solenoids.
Let n₁ and n₂ be the number of turns per unit length (n₁ = \(\frac{N_1}{l}\) and n₂ = \(\frac{N_2}{l}\)). Current in the primary coil is i.

∴ Magnetic field inside the primary (B) = µ₀n₁ I = µ₀ \(\frac{N_1}{l}\) I ……… (1)
Magnetic flux through each turn of primary
Φ_b = \(\vec{B} \cdot \vec{A}\) = µ₀ \(\frac{N_1}{l}\) I × A
The same magnetic flux is linked with secondary coil Nii „ ,,
∴ = µ₀ \(\frac{\mathrm{N}_1 \mathrm{i}}{l}\) × A × N₂ …………. (3)
If M be mutual inductance of the two coils, the total flux linked with the secondary is Mi
∴ Total magnetic flux is linked with secondary
∴ Mi = \(\frac{\mu_0 \mathrm{~N}_1 \mathrm{~N}_2 \mathrm{iA}}{l}\) ………… (4)
M = \(\frac{\mu_0 N_1 N_2 A}{l}\) ………… (5) (∵ A = πr²)
(or) M = \(\frac{\mu_0 N_1 N_2\left(\pi \mathrm{r}^2\right)}{l}\) ………… (6) (∵ µ_r = \(\frac{\mu}{\mu_0}\))

Question 17.
The wavelength of first member of Balmer Series is 6563 Å. Calculate the wavelength of second member of Lyman Series.
Solution:
\(\frac{1}{\lambda}\) = R(\(\frac{1}{n_1^2}\) – \(\frac{1}{n_2^2}\))
For 1^st member of Balmer series.
\(\frac{1}{6563}\) = R(\(\frac{1}{2^2}\) – \(\frac{1}{3^2}\))
\(\frac{1}{6563}\) = \(\frac{5 R}{36}\) ………… (1)

For 2^nd member of Lyman series.
\(\frac{1}{\lambda^1}\) = R(\(\frac{1}{1^2}\) – \(\frac{1}{3^2}\))
\(\frac{1}{\lambda^1}\) = \(\frac{8 R}{9}\) ………. (2)
\(\frac{(1)}{(2)}\) ⇒ \(\frac{\lambda^1}{6563}\) = \(\frac{5 R}{36}\) \(\frac{9}{8 R}\)
= \(\frac{5}{32}\) × 6563
∴ λ₁ = 1025.5 Å

Question 18.
Write truth tables of Universal logic gates.
Answer:
NAND gate: NAND gate is a combination of AND gate and NOT gate.

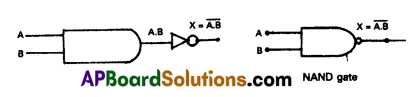
NAND gate can be obtained by connecting a NOT gate in the output of an AND gate. NAND gates are called universal gates.

i) If both inputs are low, output is high.
A = 0, B = 0, X = 1

ii) If any input is low, output is high.
A = 0, B = 1, X = 1
A = 1, B = 0, X = 1

iii) If both inputs are high, output is low.
A = 1, B = 1, X = 0

A	B	X = \( \overline{A . B} \)
0	0	1
0	1	1
1	0	1
1	1	0

NOR gate : NOR gate is a combination of OR gate and NOT gate when the output of OR gate is connected to NOT gate. It has two (or) more inputs and one output.

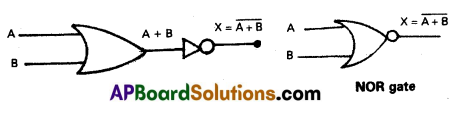
i) If both inputs are low, output is high.
A = 0, B = 0, X = 1

ii) If any input is high, the output is low.
A = 0, B = 1, X = 0
A = 1, B = 0, X = 0

iii) If both inputs are high, the output is low. A = 1, B = 1, X = 0
NOR gate is also a universal gate.

A	B	X = \(\overline{A+B}\)
0	0	1
0	1	0
1	0	0
1	1	0

Section – C (2 × 8 = 16 Marks)

Note :

• Answer ANY TWO of the following questions.
• Each question carries EIGHT marks.
• ALL are long answer type questions.

Question 19.
What is Doppler effect ? Object an expression for the apparent frequency of sound heard when the source is in motion with respect to an observer at rest.
Answer:
Doppler effect : The apparent change in the frequency heard by the observer due to the relative motion between the observer and the source of sound is called doppler effect.

When a whistling railway engine approaches an observer standing on the platform, the frequency of sound appears to increase. When it moves away the frequency appear to decrease.

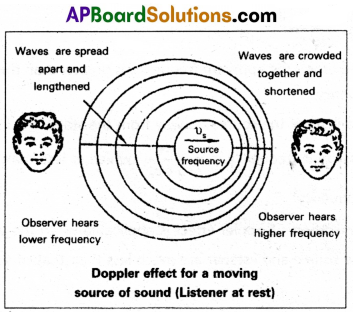
Expression for apparent frequency when source is in motion and listner at rest :
Let S = Source of sound
O = Listener
Let ‘S’ be the source, moving with a velocity ‘υ_s‘ towards the stationary listener.
The distance travelled by the source in time period ‘T’ = υ_s.T.
Therefore, the successive compressions and rarefactions are drawn closer to listener.
∴ Apparent wavelengt λ’ – λ = υ_sT.
λ’ = λ – \(\frac{υ_s}{v}\) [∵ v = \(\frac{1}{\mathrm{~T}}\)]
\(\frac{\lambda v-υ_s}{v}=\frac{v-υ_s}{v}\) (∵ υ = vλ)

If ”v” is apparent frequency heard by the listener then v’ = \(\frac{v}{\lambda^{\prime}}\), where ‘υ’ is velocity of sound in air
v’ = \(\frac{υ . v}{υ-υ_s}\)
Therefore, the apparent frequency is greater than the actual frequency.

Similarly, if the source is away from the stationary listener then apparent frequency v’ = \(\frac{υ . v}{υ+υ_s}\), which is less than tlpe actual frequency.

Limitation : Doppler effect is applicable when the velocities of the source and listener are much less than that of sound velocity.

Question 20.
a) State Kirchhoff s law for an electrical network. Using these laws deduce the condition for balance in a Wheatstone bridge.
b) The four resistors 20 Ω, 40 Ω, (20 + x) Ω , 80 Ω respectively form a Wheatstone bridge. Find the value of “x”.
Answer:
1) Kirchhoffs first law (Junction rule or KCL): The algebraic sum of the currents at any junction is zero. [∴ Σl = 0]
(or)
The sum of the currents flowing towards a junction is equal to the sum of currents away from the junction.

2) Kirchhoffs second law (Loop rule of KVL) : The algebraic sum of potential around any closed loop is zero.
∴ Σ(IR) + ΣE = 0

Wheatstone bridge: Wheatstone’s bridge circuit consists of four resistances R₁, R₂, R₃ and R₄ are connected to form a closed path. A cell of emf e is connected between the point A and C and a galvanometer is connected between the points B and D as shown in fig. The current through the various branches are indicated in the figure. The current through the galvanometer is I_g and the resistance of the galvanometer is G.

Applying Kirchhoff’s first law
at the junction D,I₁ – I₃ – I_g = 0 ……….. (1)
at the junction B, I₂ + I₄ – I4 = 0 ……….. (2)
Applying Kirchhoffs second law to the closed path ADBA,
-I₁R₁ – I_gG + I₂R₂ = 0
or
⇒ I₁R₁ + l_gG = I₂R₂ ………. (3)
applying kirchhoffs second law to the closed path DCBD,
-I₃R₃ + I₄R₄ + I_gG = 0
⇒ I₃R₃ – I_gG = IR₄ ………. (4)

When the galvanometer shows zero deflection the points D and B are at the same potential. So I_g = 0

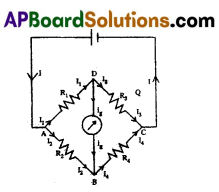
Substituting this value in (1), (2), (3) and (4).
I₁ = I₃ ……. (5)
I₂ = I₄ ……. (6)
I₁R₁ = I₂R₂ ………(7)
I₃R₃ = I₄R₄ ………. (8)
Dividing (7) by (8)
\(\frac{I_1 R_1}{I_3 R_3}=\frac{I_2 R_2}{I_4 R_4}\) ⇒ \(\frac{R_1}{R_3}=\frac{R_2}{R_1}\) [∵ I₁ = I₃ & I₂ = I₄]
∴ Wheatstone’s Bridge principle : R₄ = R₃ × \(\frac{R_2}{R_1}\)

Question 21.
a) Explain the principle and working of a nuclear reactor with the help of a labelled diagram.
Answer:
Principle : A nuclear reactor works on the principle of achieving controlled chain reaction in natural Uranium ²³⁸U enriched with ²³⁵U, consequently generating large amounts of heat.

A nuclear reactor consists of
(1) Fuel
(2) Moderator
(3) Control rods
(4) Radiation shielding
(5) Coolant.

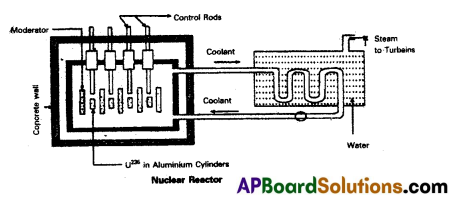
1. Fuel and clad : In reactor the nuclear fuel is fabricated in the form of thin and long cylindrical rods. These group of rods treated as a fuel assembly. These rods are surrounded by coolant, which is used to transfer of heat produced in them. A part of the nuclear reactor which use to store the nuclear fuel is called the core of the reactor. Natural uranium, enriched uranium, plutonium and uranium – 233 are used as nuclear fuels.

2. Moderator : The average energy of neutrons released in fission process is 2 MeV. They are used to slow down the velocity of neutrons. Heavy water or graphite are used as moderating materials in reactor.

3. Control rods : These are used to control the fission rate in reactor by absorbing the neutrons. Cadmium and boron are used as controlling the neutrons, in the form of rods.

4. Shielding : During fission reaction beta and gamma rays are emitted in addition to neutrons. Suitable shielding Such as steel, lead, concrete etc. are provided around the reactor to absorb and reduce the intensity of radiations to such low levels that do not harm the operating personnel.

5. Coolant: The heat generated in fuel elements is removed by using a suitable coolant to flow around them. The coolants used are water at high pressures, molten sodium etc.

Working : Uranium fuel rods are placed in the aluminium cylinders. The graphite moderator is placed in between the fuel cylinders. To control the number of neutrons, a number of control rods of cadmium or beryllium or boron are placed in the holes of graphite block. When a few ²³⁵U nuclei undergo fission fast neutrons are liberated. These neutrons pass through the surrounding graphite moderator and loose their energy to become thermal neutrons. These thermal neutrons are captured by ²³⁵U. The heat generated here is used for heating suitable coolants which in turn heat water and produce steam. This steam is made to rotate steam turbine and there by drive a generator of production for electric power.

b) Compare the radii of the nuclei of mass numbers 27 and 64.
Solution:
A₁ = 27; A₂ = 64
\(\frac{R_1}{R_2}\) = \(\frac{A_1}{A_2}\)^1/3 [∵ R = R₀A^1/3]
\(\frac{R_1}{R_2}\) = \(\left[\frac{27}{64}\right]^{\frac{1}{3}}\) = \(\frac{3}{4}\)
∴ R₁ : R₂ 3 : 4