AP Inter 2nd Year Physics Question Paper March 2019

Thoroughly analyzing AP Inter 2nd Year Physics Model Papers and AP Inter 2nd Year Physics Question Paper March 2019 helps students identify their strengths and weaknesses.

AP Inter 2nd Year Physics Question Paper March 2019

Time: 3 Hours
Maximum Marks: 60

Section – A (10 × 2 = 20)

Note :

• Answer all questions.
• Each question carries two marks.
• All are very short answer type questions.

Question 1.
A small angled ‘prism of 4° deviates a ray through 2.48°. Find the refractive index of the prism.
Answer:
A = 4°
D_m = 2.48°
D_m = A(μ – 1)
μ – 1 = \(\frac{\mathrm{D}_{\mathrm{m}}}{\mathrm{A}}=\frac{2.48}{\mathrm{~A}}\) = 0.62
μ = 1 + 0.62
μ = 1.62

Question 2.
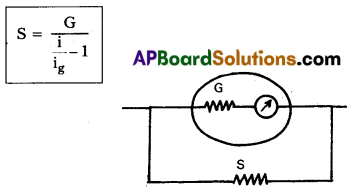
How do you covert a moving coil galvanometer into an ammeter ?
Answer:
A small resistance is connected in parallel to the moving coil galvanometer, then it converts to Ammeter.

Question 3.
Magnetic lines from continuous closed loop. Why?
Answer:
Magnetic lines of forces always start from north pole and forming curved path, enter south pole and travel to north pole inside the magnet. Thus lines of force are forming closed loop.

Question 4.
Classify the following materials with regard to magnetism :
Bismuth, Cobalt, Oxygen, Copper.
Answer:
Ferromagnetic materials → Cobalt, Nickel.
Paramagnetic materials → Oxygen,
Manganese Diamagnetic materials → Bismuth, Copper.

Question 5.
A transformer converts 200V ac into 2000 V ac. Calculate the number of turns in the secondary, if the primary has 10 turns.
Answer:
\(\frac{V_S}{V_p}=\frac{N_s}{N_p}\)
V_p = 200V, V_s = 2000V, N_p = 10
N_s = \(\frac{V_s}{V_p}\) × N_p = \(\frac{2000}{200}\) × 100
N_s = 100.

Question 6.
Give two uses of infrared rays.
Answer:

1. Infrared radiation plays an important role in maintaining the Earth warm.
2. Infrared lamps are used in physical therapy.
3. Infrared detectors are used in Earth Satellites.
4. These are used in taking photographs during the conditions of fog, smoke etc.

Question 7.
State Heisenberg’s uncertainty principle.
Answer:
Uncertainity principle states that “it is impossible to measure both position (Δx) and momentum of an electron (Δp) [or any other particle] at the same time exactly”, i.e., Δx . Δp ≈ h where Δx is uncertainty in the specification of position and Δp is uncertainty in the specification of momentum.

Question 8.
What is ‘Work function’ ?
Answer:
The minimum energy required to liberate an electron from photometal surface is called work function, Φ₀.

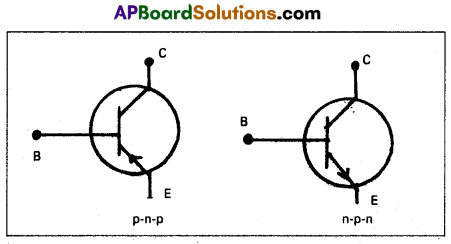
Question 9.
Draw the circuit symbols for p-n-p and n-p-n transistors.
Answer:

Question 10.
Mention the basic methods of modulation.
Answer:
The basic methods of modulation are :

1. Amplitude modulation (AM)
2. Frequency modulation (FM)
3. Phase modulation (PM).

Section – B (6 × 4 = 24)

Note:

• Answer any six of the following questions.
• Each question carries four marks.
• All are short answer type questions.

Question 11.
Define focal length of a concave mirror. Prove that the radius of curvature of a concave mirror is double its focal length.
Answer:
Focal length of concave mirror : The distance between the focus F and the pole P of the mirror is called the focal length of the concave mirror.

Consider a ray AB parallel to principal axis incident on a concave mirror at B and is reflected along BF. The line CB is normal to the mirror.

Let θ be the angle of incidence, ∠ABC = ∠BCP = θ

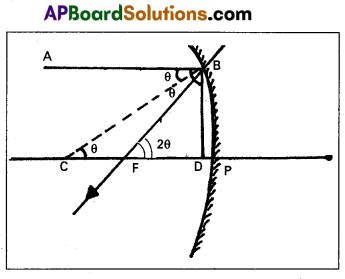
Draw BD ⊥ CP
In right angled Δ^le BCD
tan θ = \(\frac{B D}{C D}\) ………… (1)
From Δ^le BFD, tan 2θ = \(\frac{B D}{F D}\) ……….. (2)
Dividing eq (2) by eq (1), \(\frac{\tan 2 \theta}{\tan \theta}=\frac{C D}{F D}\) ……….. (3)
If θ is very small, then tan θ ≈ θ and tan 2θ ≈ 2θ since the aperture of the lens is small.
∴ The point B lies very close to p.
CD ≈ CP and FD ≈ FP
From eq.(3), \(\frac{2 \theta}{\theta}=\frac{C P}{F P}=\frac{R}{f}\) ⇒ 2 = \(\frac{R}{f}\)
R = 2f

Question 12.
How do you determine the resolving power of your eye ?
Answer:
Make black strips of equal width separated by white strips. All the black strips having same width, while the width of white strips should increase from left to right.

Now watch the pattern with one eye. By moving away (or) closer to the wall, find the position where you can just see some two black strips as separate strips.

All black strips to the left of this strips would merge into one another and would not be distinguishable on the other hand, the black strips to the right of this would be more and more clearly visible.

Note the width d of the white strips and measure the distance D of the wall from eye.

Then resolution of your eye = \(\frac{\mathrm{d}}{\mathrm{D}}\)

Question 13.
Derive an expression for the intensity of the electric field at a point on the axial line of an electric dipole.
Answer:
Electric Held at a point on the axis of a dipole :
1) Consider an electric dipole consisting of two charges – q and +q separated by a distance ‘2a’ with centre ‘O’.
2) We shall calculate electric field E at point P on the axial line of dipole, and at a distance OP = r.

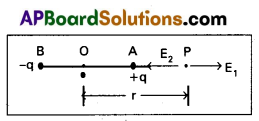
3) Let E₁ and E₂ be the intensities of electric field at P due to charges +q and – q respectively.

Question 14.
Explain the behaviour of dielectrics in an external field.
Answer:
1) When an external field is applied across dielectrics, the centre of positive charge distribution shifts in the direction of electric field and that of the negative charge distribution shifts opposite to the electric field and induce a net electric field within the medium opposite to the external field. In such situation the molecules are said to be polarised.

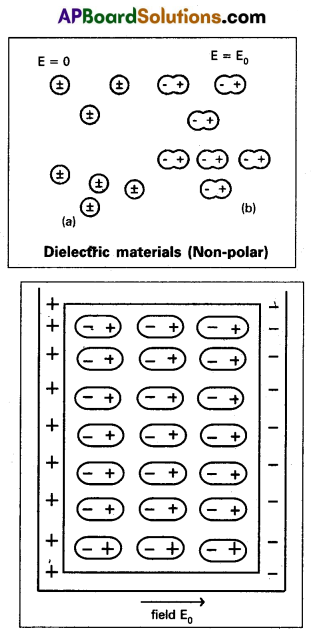
2) Now consider a capacitor with a dielectric between the plates. The net field in the dielectric becomes less.

3) If E₀is the external field strength and E_i is the electric field strength induced, then the net field
\(\overrightarrow{\mathrm{E}}_{\text {net }}=\overrightarrow{\mathrm{E}}_{\mathrm{O}}=\overrightarrow{\mathrm{E}}_{\mathrm{i}}\)
(E_net) = E₀ – E_i = \(\frac{E}{K}\)
where K is the dielectric constant of the medium.

Question 15.
A100 turn closely wound circular coil of radius 10 cm carries a current of 3.2 A
a) What is the field at the centre of the coil ?
b) What is the magnetic moment of this coil ?
Answer:
a) From B = \(\frac{\mu_0 \mathrm{NI}}{2 \mathrm{R}}\)
Here N = 100
I = -3.2 A and R = 0.1 M
B = \(\frac{4 \pi \times 10^{-7} \times 10^2 \times 3.2}{2 \times 10^{-1}}\)
= \(\frac{4 \pi \times 10^{-5} \times 10}{2 \times 10^{-1}}\) (Usmg π × 3.2 – 10)
B = 2 × 10^-3 T
The direction is given by the right hand thumb rule.

b) The magnetic moment is given by,
m = NIA = NIπr²
= 100 × 3.2 × 3.14 × 10^-2
= 10 Am²

Question 16.
Describe the ways in which Eddy currents are used to advantage.
Answer:
Eddy currents are used to advantage in :
i) Magnetic breaking in trains :
A strong magnetic field is applied across the metallic drum rotating with the axle of the electric train. Thus large eddy currents are produced in the metallic drum. These currents oppose the motion of the drum and hence the axle of the train which ultimately makes the train come to rest.

ii) Induction Motor :
Eddy currents are used to rotate the short circuited rotor of an induction motor. Ceiling fans are also induction motors which ruft on single phase alternating current.

iii) Electromagnetic damping :
Certain galvanometers have a fixed core made of non magnetic metallic material. When the coil oscillates, the eddy currents generated in the core oppose the motion and bring the coil to rest quickly.

iv) Induction furnace :
Induction furnace can be used to produce high temperatures and can be utilised to prepare alloys, by melting the constituent metals. A high frequency alternating current is passed through a coil. The eddy currents generated in the metals produce high temperatures sufficient to melt it.

v) Analogue energy meters :
Concept of eddy currents is used in energy meters to record the consumption of electricity. Aluminium disc used in these meters get induced due to varying magnetic field. It rotates due to eddy currents produced in it.

Question 17.
Explain the different types of spectral lines.
Answer:
Spectral series of Hydrogen atom :

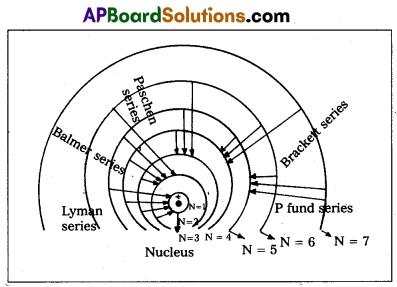
Hydrogen atom has five series of spectral lines. They are :

1. Lyman series :
When an electron jumps from the outer orbits to the first orbit, the spectral lines are in the ultra – violet region.
Here n₁ = 1, n₂ = 2, 3, 4, 5….
\(\frac{1}{\lambda}=\mathrm{R}\left[\frac{1}{1^2}-\frac{1}{\mathrm{n}_2^2}\right]=\mathrm{R}\left[1-\frac{1}{\mathrm{n}_2^2}\right]\)

2) Balmer Series:
When an electron jumps from the outer orbits to the second orbit, the spectral lines are in the visible region.
Here n₁ = 2, n₂ = 3, 4, 5…
\(\frac{1}{\lambda}=\mathrm{R}\left[\frac{1}{2^2}-\frac{1}{\mathrm{n}_2^2}\right]\)

3) Paschen series : When an electron jumps from the outer orbit to the third orbit, the spectral lines are in the near infrared region.
Here n₁ = 3, n₂ = 4, 5, 6 ….
\(\frac{1}{\lambda}=\mathrm{R}\left[\frac{1}{3^2}-\frac{1}{\mathrm{n}_2^2}\right]\)

4) Brackett series : When an electron jumps from outer orbits to the fourth orbit, the spectral lines are in the infrared region.
Here n₁ = 4, n₂ = 5, 6, 7 …….
\(\frac{1}{\lambda}=\mathrm{R}\left[\frac{1}{4^2}-\frac{1}{\mathrm{n}_2^2}\right]\)

5) Pfund series : When an electron jumps from outer orbits to the fifth orbit, the spectral lines are in the far infrared region.
Here n₁ = 5, n₂ = 6, 7, 8, ……
\(\frac{1}{\lambda}=\mathrm{R}\left[\frac{1}{5^2}-\frac{1}{\mathrm{n}_2^2}\right]\)

Question 18.
Distinguish between half-wave and full-wave Rectifiers.
Answer:

Half wave rectifier	Full wave rectifier
1. Single diode is used.	1. Two diodes are used.
2. Only half wave is rectified.	2. Full wave is rectified.
3. Rectifier efficiency η = \(\frac{0.406 R_L}{r_f+R_L}\)	3. Rectifier efficiency η = \(\frac{0.812 R_L}{r_f+R_L}\)
4. Efficiency of half wave rectifier is 40.6%.	4. Efficiency of full wave rectifier is 81.2%.
5. Output is discontinuous and pulsative.	5. Output is continuous and pulsative.

Section – C (2 × 8 = 16)

Note :

• Answer any two of the following questions.
• Each question carries eight marks.
• All are long answer type questions.

Question 19.
a) Explain the formation of stationary waves in stretched strings and hence deduce the laws of transverse waves in stretched strings.
Answer:
A string is a metal wire whose length is large when compared to its thickness. A stretched string is fixed at both ends, when it is plucked at mid point, two reflected waves of same amplitude and frequency at the ends are travelling in opposite direction and overlap along the length. Then the resultant waves are known as the standing waves (or) stationary waves.

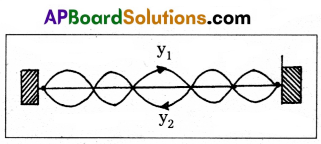
Let two transverse progressive waves of same amplitude a, wave length λ and frequency ‘v’, travelling in opposite direction be given by
y₁ = a sin (kx – ωt) and y₂ = a sin (kx + ωt)
where ω = 2π v and k = \(\frac{2 \pi}{\lambda}\)
The resultant wave is given by y = y₁ + y₂
y = a sin (kx – ωt) + a sin (kx + ωt)
y = (2a sin kx) cos ωt
2a sin kx = Amplitude of resultant wave.
It depends on ‘kx’. If x = 0, \(\frac{\lambda}{2}, \frac{2 \lambda}{2}, \frac{3 \lambda}{2}\) … etc,
the amplitude = zero
These position are known as “Nodes”.
If x = \(\frac{\lambda}{4}, \frac{3 \lambda}{4}, \frac{5 \lambda}{4}\) ……. etc, the amplitude = maximum (2a).
These positions are called “Antinodes”.
If the string vibrates in ‘P’ segments and ‘l’ is its length then length of each segment = \(\frac{l}{\mathrm{P}}\)
Which is equal to \(\frac{\lambda}{2}\)
∴ \(\frac{l}{\mathrm{P}}=\frac{\lambda}{2}\) ⇒ λ = \(\frac{2 l}{\mathrm{P}}\)
Harmonic frequency v = \(\frac{v}{\lambda}=\frac{v P}{2 l}\)
v = \(\frac{υ \mathrm{P}}{2 l}\) ………….. (1)
If ‘T’ is tension (stretching force) in the string and ‘μ’ is linear density then velocity of transverse wave (v) in the string is
v = \(\sqrt{\frac{T}{\mu}}\) ……. (2)
From the Eqs (1) and (2)
Harmonic frequency v = \(\frac{\mathrm{P}}{2 l} \sqrt{\frac{\mathrm{T}}{\mu}}\)
If P = 1 then it is called fundamental frequency (or) first harmonic frequency
∴ Fundamental Frequency v = \(\frac{1}{2 l} \sqrt{\frac{\mathrm{T}}{\mu}}\) ………. (3)

Laws of Transverse Waves Along Stretched String :
Fundamental frequency of the vibrating string v = \(\frac{1}{2 l} \sqrt{\frac{\mathrm{T}}{\mu}}\)

First Law : When the tension (T) and linear density (μ) ,are constant, the fundamental frequency (v) of a vibrating string is inversely proportional to its length.
∴ v ∝ \(\frac{1}{l}\)
⇒ v l = constant, when T and ‘μ’ are constant.

Second Law : When the length (l) and its, linear density (m) are constant the fundamental frequency of a vibrating string is directly proportional to the square root of the stretching force (T).
∴ v ∝ √T
⇒ \(\frac{v}{\sqrt{T}}\) = constant, when ‘l’ and ‘m’ are constant.

Third Law: When the length (l) and the tension (T) are constant, the fundamental frequency of a vibrating string is inversely propor¬tional to the square root of the linear density (m).
∴ v ∝ \(\frac{1}{\sqrt{\mu}}\)
⇒ v√μ = constant, when ‘l’ and ‘T’ are constant.

b) A steel wire 0.72 m long has a mass of 5.0 × 10^-3 kg. If the wire is under a tension of 60N. What is the speed of transverse waves on the wire ?
Solution:
Mass per unit length of the wire,
μ = \(\frac{5.0 \times 10^{-3} \mathrm{~kg}}{0.72 \mathrm{~m}}\) = 6.9 × 10^-3 kg m^-1
Tension, T = 60 N
The speed of wave on the wire is given by
υ = \(\sqrt{\frac{\mathrm{T}}{\mu}}=\sqrt{\frac{60 \mathrm{~N}}{6.9 \times 10^{-3} \mathrm{~kg} \mathrm{~m}^{-1}}}\) = 93ms^-1

Question 20.
a) State Kirchhoffs law for an electrical network. Using these laws deduce the condition for balance in a Wheatstone bridge.
Answer:
1) Kirchhoffs first law (Junction rule or KCl.) : The algebric sum of the current at any junction is zero.
∴ ΣI = 0
(or)
The sum of the currents flowing towards a junction is equal to the sum of currents away from the junction.

2) Kirchhoffs second law (Loop rule or KVL) : The algebric sum of potential around any closed loop is zero.
∴ Σ(IR) + ΣE = 0

Wheatstone bridge : Wheatstone’s bridge circuit consists of four resistances R₁, R₂, R₃ and R₄ are connected to form a closed path. A cell of emf e is connected between the point A and C and a galvanometer is connected between the points B and D as shown in figure. The current through the various branches are indicated in the figure. The current through the galvanometer is I_g and the resistance of the galvanometer is G.
Applying Kirchhoffs first law
at the junction D, I₁ – I₃ – I_g = 0 ……….. (1)
at the junction B, I₂ + I_g – I₄ = 0 ……….. (2)
Applying Kirchhoffs second law to the closed path ADBA,
-I₁R₁ – I_gG + I₂R₂ = 0
or
⇒ I₁R₁ + I_gG = I₂R₂ ……….. (3)
Applying kirchhoffs second law to the closed path DCBD,
-I₃R₃ + I₄R₄ + T_gG = 0
I₃R₃ – I_gG = I₄R₄ ………… (4)

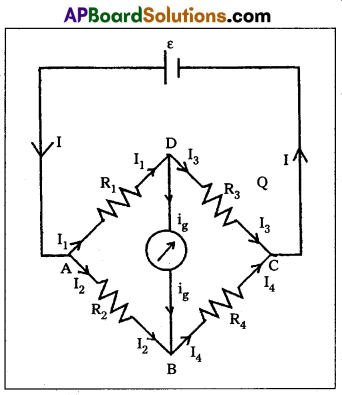
When the galvanometer shows zero deflection the points D
and B are at the same potential. So I_g = 0.
Substituting this value in (1), (2), (3) and (4).
I₁ = I₃ ……….. (5)
I₂ = I₄ ………. (6)
I₁R₁ = I₂R₂ ………. (7)
I₃R₃ = I₄R₄ …………. (8)
Dividing (7) by (8)
\(\frac{I_1 R_1}{I_3 R_3}=\frac{I_2 R_2}{I_4 R_4}\) ⇒ \(\frac{R_1}{R_3}=\frac{R_2}{R_1}\) [∵ I₁ = I₃ & I₂ = I₄]
∴ Wheatstone’s Bridge principle: R₄ = R₃ × \(\frac{\mathbf{R}_2}{\mathrm{R}_1}\)

b) A wire of resistance 4R is bent in the form of a circle. What is the effective resistance between the ends of the diameter ?
Solution:
Resistance of long wire = 4R
Hence the resistance of half wire = \(\frac{4 R}{2}\) = 2R

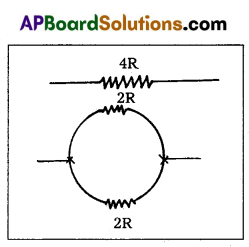
Now these two wire are connected in parallel. Hence the effective resistance between the ends of the diameter
R_p = \(\frac{R_1 R_2}{R_1+R_2}\)
⇒ R_p = \(\frac{2 R \times 2 R}{2 R+2 R}\)
∴ R_p = R.

Question 21.
Explain the principle and working of a nuclear reactof with the help of a labelled diagram.
Answer:
Principle: A nuclear reactor works on the principle of achieving controlled chain reaction in natural Uranium ²³⁸U enriched with ²³⁵U, consequently generating large amounts of heat.

A nuclear reactor consists of
(1) Fuel
(2) Moderator
(3) Control rods
(4) Radiation shielding
(5) Coolant.

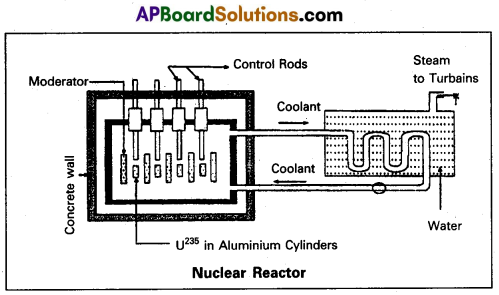
1) Fuel and clad: In reactor the nuclear fuel is fabricated in the form of thin and long cylindrical rods. These group of rods treated as a fuel assembly. These rods are surrounded by coolant, which is used to transfer of heat produced in them. A part of the nuclear reactor which use to store the nuclear fuel is called the core of the reactor. Natural uranium, enriched uranium, plutonium and uranium – 233 are used as nuclear fuels.

2) Moderator : The average energy of neutrons, released in fission process is 2 MeV. They are used to slow down the velocity of neutrons. Heavy water or graphite are used as moderating materials in reactor.

3) Control Rods : These are used to control the fission rate in reactor by absorbing the neutrons. Cadmium and boron are used as controlling the neutrons, in the form of rods.

4) Shielding: During fission reaction beta and gamma rays are emitted in addition to neutrons. Suitable shielding such as steel, lead, concrete etc are provided around the reactor to absdrb and reduce the intensity of radiations to such low levels that do not harm the operating personnel.

5) Coolant: The heat generated in fuel elements is removed by using a suitable coolant to flow around them. The c&olants used are water at high pressures, molten sodium etc.

Working : Uranium fuel rods are placed in the aluminium cylinders. The graphite moderator is placed in between the fuel cylinders. To control the number of neutrons, a number of control rods of cadmium or beryllium or boron are placed in the holes of graphite block. When a few ²³⁵U nuclei undergo fission fast neutrons, are liberated. These neutrons pass through the surrounding graphite moderator and loose their energy to become thermal neutrons. These thermal neutrons are captured by ²³⁵U. The heat generated here is used for heating suitable coolants which in turn heat water and produce steam. This steam is made to rotate steam turbine and there by drive a generator of production for electric power.