AP Inter 2nd Year Physics Question Paper March 2017

Thoroughly analyzing AP Inter 2nd Year Physics Model Papers and AP Inter 2nd Year Physics Question Paper March 2017 helps students identify their strengths and weaknesses.

AP Inter 2nd Year Physics Question Paper March 2017

Time: 3 Hours
Maximum Marks: 60

Section – A (10 × 2 = 20)

Note :

• Answer all questions.
• Each question-carries two marks.
• All are very short answer type questions.

Question 1.
Define ‘Power’ of a Convex Lens. What is its unit ?
Answer:
Power of a lens: Power of a lens is defined as its bending ability and is measured as reciprocal of focal length in metre.
∴ Power of a lens (P) = \(\frac{1}{f(\text { in metres) }}\) = \(\frac{100}{\mathrm{f}(\text { in cms })}\)
Unit → Dioptre (D)

Question 2.
Distinguish between Ammeter and Voltmeter.
Answer:

Ammeter	Voltmeter
1. It is used to measure current.	1. It is used to measure P.D. between two points.
2. Resistance of an ideal Ammeter is zero.	2. Resistance of ideal voltmeter is infinity.
3. It is connected in series in the circuits.	3. It is connected in parallel inthe circuits.

Question 3.
Define Magnetic Inclination or angle of Dip.
Answer:
Inclination or Dip (I) : The angle which the total intensity of earth’s magnetic field makes with the horizontal at any place is called inclination (I).

Question 4.
Classify the following materials with regard to magnetism : Manganese, Cobalt, Nickel, Bismuth, Oxygen, Copper
Answer:
Ferromagnetic materials → Cobalt, Nickel
Para magnetic materials → Oxygen, Manganese
Diamagnetic materials → Bismuth, Copper .

Question 5.
What type of trasnformer is used in a 6 V bed lamp ?
Answer:
Step down transformer is used in 6V bed lamp.

Question 6.
What are the applications of microwaves ?
Answer:

1. Microwaves are used in Radars.
2. Micorwaves are used for cooking purposes.
3. A radar using microwave’can help in detecting the speed of auto mobile in motion.

Question 7.
What are the Cathode Rays ?
Answer:
Fast moving electrons are called cathode rays.

Question 8.
What is “Photoelectric Effect” ?
Answer:
When light of sufficient energy is incident on the photometal surface, electrons are emitted. This phenomenon is called photoelectric effect.

Question 9.
What is a p-type semiconductor ? What are the majority and minority charge carriers in it ?
Answer:
If a trivalent inpurity is added to a tetravalent semiconductor, it is called p-type semi-condutor.
In p-type semiconductor majority charge carriers are holes and minority charge carriers are electrons.

Question 10.
Define Modulation. Why is it necessary ?
Answer:
Modulation : The process of combining low frequency audio signal with high frequency carrier wave is called modulation.

The audio frequency signals cannot be transmitted over long distances faithfully. Therefore they are ceombined with high frequency waves and trasmitted.

Section – B (6 × 4 = 24)

Note :

• Answer any six of the following questions.
• Each question carries four marks.
• All are short answer type questions.

Question 11.
Define focal length of a concave mirror. Prove that the radius of curvature of a concave mirror is double its focal length.
Answer:
Focal length of concave mirror:
The distance between the focus F and the pole P of the mirror is called the focal length of the concave mirror.

Consider a ray AB parallel to principal axis incident on a concave mirror at B and is reflected along BF. The line CB is normal to the mirror.

Let θ be the angle of incidence, ∠ABC = ∠BCP = θ
Draw BD ⊥ CP
In right angled Δ^le BCD

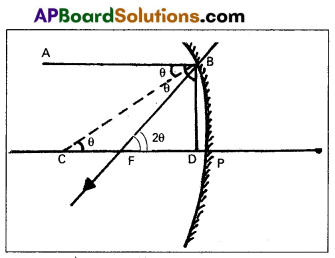
Tan θ = \(\frac{B D}{C D}\) ……… (1)
From Δ^le BFD, Tan2θ = \(\frac{B D}{F D}\) ………….. (2)
Dividing eq (2) by eq (1), \(\frac{{Tan} 2 \theta}{{Tan} \theta}=\frac{C D}{F D}\) ………….. (3)
If θ is very small, then tan θ = θ and tan 2θ = 2θ since the aperture of the lens is small
The point B lies very close to p.
CD = CP and FD = FP
From eq (3), \(\frac{2 \theta}{\theta}=\frac{C P}{F P}=\frac{R}{f}\) ⇒ 2 = \(\frac{R}{f}\)

Question 12.
How do you determine the resolving power of your eye ?
Answer:
Make black strips of equal width separated by white strips. All the black strips having same width, while the width of white strips should increase from left to right.

Now watch the pattern with one eye. By moving away (or) closer to the wall, find the position where you can just see some two black strips as separate strips.

All black strips to the left of this strips would merge into one another and would not be distinguishable on the other hand, the black strips to the right of this would be more and more clearly visible.

Note the width d of the white strips and measure the distance D of the wall from eye.
Then resolution of your eye = \(\frac{d}{D}\).

Question 13.
Derive an expression for the intensity of the electric field at a point on the axial line of an electric dipole.
Answer:
Electric field at a point on the axis of a dipole :
1) Consider an electric dipole consisting of two charges -q and +q separated by a distance ‘2a’ with centre ‘O’.

2) We shall calculate electric field E at point P on the axial line of dipole, and at a distance OP = r.

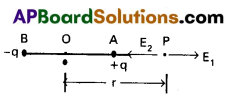
3) Let E₁ and E₂ be the intensities of electric field at P due to charges +q and -q respectively.

Question 14.
Three capacitors of capacitances 2 PF, 3 PF and 4 PF are connected in parallel.
(a) What is the total capacitance of the combination ?
(b) Determine the charge on each capacitor if the combination is connected to a 100 V supply.
Answer:
C₁ = 2 × 10^-12 F, C₂ = 3 × 10^-12 F, C₃ = 4 × 10^-12 F

(a) Total capacitance in parallel combination is
C = C₁ + C₂ + C₃ = (2 + 3 + 4)₁₀^-12 = 9PF

(b) Given V= 100 V
q₁ = C₁V = 2 × 10^-12 × 100 = 2 × 10^-10 C
q₂ = C₂V = 3 × 10^-12 × 100 = 3 × 10^-10C
q₃ = C₃V = 4 × 10^-12 × 100 = 4 × 10^-10C

Question 15.
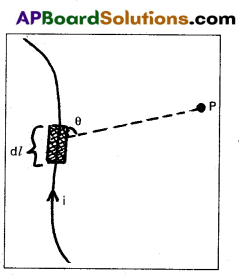
State and explain Biot-Savart Law.
Answer:
Consider a very small element of length dl of a conductor carrying current (i). Magnetic induction due to small element at a point P distance r form the element.

Magnetic induction (dB) is directly proportional to

1. current
2. Length of the element (dl)
3. sine angle between r and dl and
4. Inversely proportional to the square of the distance from small element to point P.

dB α = \(\frac{\mathrm{id} l \sin \theta}{\mathrm{r}^2}\)
dB = \(\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{id} l \sin \theta}{\mathrm{r}^2}\)
where ₀ = permeability in free space.
\(\frac{\mu_0}{4 \pi}\) = 10^-7 Wb m^-1 A^-1
IN vector form \(\overrightarrow{\mathrm{dB}}=\frac{\mu_0 \mathrm{i}}{4 \pi} \frac{(\overrightarrow{\mathrm{d} l} \times \overrightarrow{\mathrm{r}})}{\mathrm{r}^3}\)

Question 16.
Describe the ways in which Eddy Currents are used to advantage.
Answer:
Eddy currents are u(sed to advantage in
i) Magnetic brakingin trains: A strong magnetic field is applied across the metallic drum rotating with the axle of the electric train. Thus large eddy currents are produced in the metallic drum. These currents oppose the motion of the drum and hence the axle of the train which ultimately makes the train come to rest.

ii) Induction Motor: Eddy currents are used to rotate the short circuited rotor of an induction motor. Ceiling fans are also induction motors which run on single phase alternating current.

iii) Electromagnetic damping : Certain galvanometers have a fixed core made of non magnetic metallic material. When the coil oscillates, the eddy currents generated in the core oppose the motion and bring the coil to rest quickly.

iv) Induction furnace: Induction furnace can be used to produce high temperatures and can be utilised to prepare ailoys, by melting the constituent metals. A high frequency alternating current is passed through a coil. The eddy currents generated in the metals produce high temperatures sufficient to melt it.

v) Analogue energy meters : Concept of eddy currents is used in energy meters to record the consumption of electricity. Aluminium disc used in these meters get induced due to varying magnetic field. It rotates due to eddy currents produced in it.

Question 17.
What are the limitations of Bohr’s theory of hydrogen atom ?
Answer:
Limitations of Bohr’s theory of Hydrogen atom :

1. This theory is applicable only to simplest atom like hydrogen, with z = 1. The theory fails in case of atoms of other elements for which z > 1.
2. The theory does not explain why orbits of electrons are taken as circular, while elliptlical orbits are also possible.
3. Bohr’s theory does not say anything about the relative intensities of spectral lines.
4. Bohr’s theory does not take into account the wave properties of electrons.

Question 18.
Distinguish between Half-wave and Full-wave rectifiers.
Answer:

Half wave rectifier	Full wave rectifier
1. Single diode is used.	1. Two diodes are used.
2. Only half wave is rectified.	2. Full wave is rectified.
3. Rectifier efficiency η = \(\frac{0.406 R_L}{r_f+R_L}\)	3. Rectifier efficiency η = \(\frac{0.812 R_L}{r_f+R_L}\)
4. Efficiency of half wave rectifier is 40.6%.	4. Efficiency of full wave rectifier is 81.2%.
5. Output is discontinuous and pulsative.	5. Output is continuous and pulsative.

Section – C (2 × 8 = 16)

Note :

• Answer any two of the following questions.
• Each question carries eight marks.
• All are long answer type questions.

Question 19.
Explain the formation of Stationary waves in an air column enclosed in open pipe. Derive the equations for the frequencies of the harmonics produced.
A closed organ pipe 70 cm long is sounded. If the velocity of sound is 331 m/s, what is the fundamental frequency of vibration of the air column ?
Answer:
(i) A pipe, which is opened at both ends is called open pipe. When a sound wave is sent through a open pipe, which gets reflected by the earth. Then incident and reflected waves are in same frequency, travelling in the opposite directions are super -imposed stationary waves are formed.

Harmonics in open pipe : To form the stationary wave in open pipe, which has two anti nodes at two ends of the pipe with a node between them.

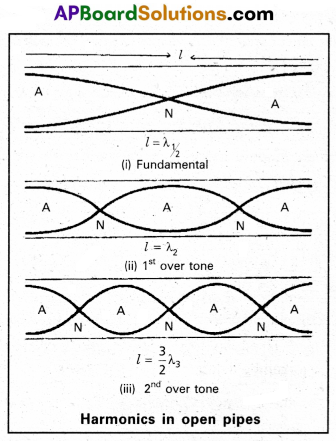
∴ The vibrating length (l)
= half of the wavelength (\(\frac{\lambda_1}{2}\))
l = \(\frac{\lambda_1}{2}\) ⇒ λ₁ = 2l

fundamental frequency v₁ = \(\frac{v}{\lambda_1}\) where v is velocity of sound in
air v₁ = \(\frac{υ}{21}\) = v ……… (1)
For second harmonic (first overtone) will have one more node and antinode than the fundamental. ‘
If λ₂ is wavelength of second harmonic l = \(\frac{2 \lambda_2}{2}\) ⇒ λ₂ = \(\frac{21}{2}\)
If v₂ is frequency of second harmonic then
v₂ = \(\frac{υ}{\lambda_2}=\frac{v \times 2}{2 l}\) = 2v
v₂ = 2v ………. (2)

Similarly for third harmonic (second overtone) will have three nodes and four antinodes as shown in above figure.
If λ₃ is wave length of third harmonic l = \(\frac{3 \lambda_3}{2}\)
λ₃ = \(\frac{21}{3}\)
If ‘v₂‘ is frequency of third harmonic then
v₃ = \(\frac{v}{\lambda_3}=\frac{v \times 3}{2 l}\) = 3v
v₃ = 3v ………. (3)

Similarly we can find the remaining or higher harmonic frequencies i.e v₃, v₄ etc, can be determined in the same way.
Therefore the ratio of the harmonic frequencies in open pipe can be written as given below.
v : v₁ : v₂ = 1 : 2 : 3 ………….

ii) l = 70 cm
= 70 × 10^-2m; v = 331 m/s ;
v = ?
v = \(\frac{v}{4 l}=\frac{331}{4 \times 70 \times 10^{-2}}\)
= 118.2 Hz.

Question 20.
State the working principle of potentiometer. Explain with the help of circuit diagram how the emf of two primary cells are compared by using the potentiometer.
A potentiometer wire is 5 m long and a potential difference of 6 V is maintained between its ends. Find the emf of a cell which balances against a length of 180 cm of the potentiometer wire.
Answer:
Working principle of potentiometer : The potential difference across a length of the potentiometer wire is directly proportional to its length (or) when a steady current is passed through a uniform wire, potential drop per unit length or potential gradient is constant.
i.e. ε ∝ l ⇒ ε = Φl where Φ is potential gradient.

Comparing the emf of two cells ε₁ and ε₂ :

• To compare the emf of tWo cells of emf E₁ and E₂ with potentiometer is shown in diagram.

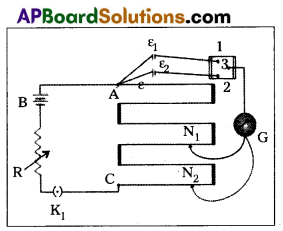
• The points marked 1, 2, 3 form a two way key.
• Consider first a position of the key where 1 and 3 are connected so that the galvanometer is connected to ε₁.
• The Jockey is moved along the wire till at a point N₁ at a distance l₁ from A, there is no deflection in the galvanometer.
  Then ε₁ ∝ l₁ ⇒ ε₁ = Φl₁ (1)
• Similarly, if another emf ε₂ is balanced against
  l₂ (AN₂), then ε₂ ∝ l₂ ⇒ ε₂ = Φl₂ (2)
• \(\frac{(1)}{(2)} \Rightarrow \frac{\varepsilon_1}{\varepsilon_2}=\frac{l_1}{l_2}\)

ii) Length of potentiometer wire L = 5m
Potential difference V = 6 Volt
Potential gradient Φ = \(\frac{V}{L}=\frac{6}{5}\) = 1.2 V/m
Balancing length l = 180cm = 1.80m
Emf of the cell E = Φl
= 1.2 × 1.8 = 2.16V.

Question 21.
Explain the principle and working of a nuclear reactor with the help of a labelled diagram.
Answer:
Principle : A nuclear reactor works on the principle of achieving controlled chain reaction in natural Uranium 238U enriched with ²³⁸U, consequently generating large amounts of heat.

A nuclear reactor consists of (1) Fuel (2) Moderator (3) Control rods (4) Radiation shielding (5) Coolant.

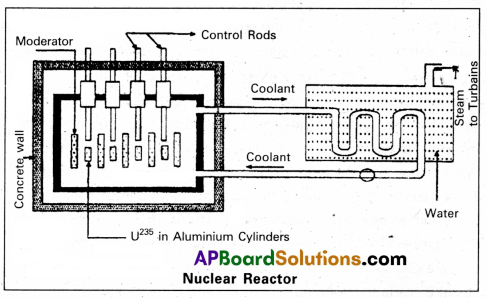
1. Fuel and clad : In reactor the nuclear fuel is fabricated in the form of thin and long cylindrical rods. These group of rods treated as a fuel assembly. These rods are surrounded by coolant, which is used to transfer of heat produced in them. A part of the nuclear reactor which use to store the nuclear fuel is called the core of the reactor. Natural uranium, enriched uranium, plutonium and uranium – 233 are used as nuclear fuels.

2. Moderator: The average energy of neutrons released in fission process is 2 MeV. They are used to slow down the velocity of neutrons. Heavy water or graphite are used as moderating materials in reactor.

3. Control Rods : These are used to control the fission rate in reactor by absorbing the neutrons. Cadmium and boron are used as controlling the neutrons, in the form of rods.

4. Shielding : During fission reaction beta and gamma rays are emitted in addition to neutrons. Suitable shielding such as steel, lead, concrete etc are provided around the reactor to absorb and reduce the intensity of radiations to such low levels that do not harm the operating personnel.

5. Coolant: The heat generated in fuel elements is removed by using a suitable coolant to flow around them. The coolants used are water at high pressures, molten sodium etc.

Working : Uranium fuel rods are placed in, the aluminium cylinders. The graphite moderator is placed in between the fuel cylinders. To control the number of neutrons, a number of control rods of cadmium or beryllium or boron are placed in the holes of graphite block. When a few ²³⁵U nuclei undergo fission fast neutrons are liberated. These neutrons pass through the surrounding graphite moderator and loose their energy to become thermal neutrons. These thermal neutrons are captured by ²³⁵U. The heat generated here is used for heating suitable coolants which in turn heat water and produce steam. This steam is made to rotate steam turbine and there by drive a generator of production for electric power.