AP Inter 2nd Year Maths 2A Model Paper Set 2 with Solutions

Thoroughly analyzing AP Inter 2nd Year Maths 2A Model Papers Set 2 helps students identify their strengths and weaknesses.

AP Inter 2nd Year Maths 2A Model Paper Set 2 with Solutions

Time: 3 Hours
Maximum Marks: 75

Note: This Question Paper consists of three sections A, B, and C.

Section – A
(10 × 2 = 20 Marks)

I. Very Short Answer type Questions.

• Answer all Questions.
• Each Question carries 2 marks.

Question 1.
If √3 + i = r(cos θ + i sin θ), then find the value of θ in radian measure.
Solution:
Given that √3 + i = r (cos θ + i sin θ)
⇒ r cos θ = √3 , r sin θ = 1
⇒ r² (cos²θ + sin²θ) = 3 + 1
⇒ r² = 4
⇒ r = 2
∴ cos θ = \(\frac{\sqrt{3}}{2}\) and sin θ = \(\frac{1}{2}\)
Hence θ = \(\frac{\pi}{6}\)

Question 2.
Find the multiplicative inverse of √5 + 3i.
Solution:
The multiplicative inverse of a + ib is \(\frac{a-i b}{a^2+b^2}\)
∴ Multiplicative inverse of √5 + 3i = \(\frac{\sqrt{5}-3 i}{(\sqrt{5})^2+3^2}=\frac{\sqrt{5}-3 i}{5+9}=\frac{\sqrt{5}-3 i}{14}\)

Question 3.
If 1, ω, ω² are the cube roots of unity, then find the value of (1 – ω) (1 – ω²) (1 – ω⁴) (1 – ω⁸).
Solution:
Since 1, ω, ω² are the cube roots of unity
⇒ 1 + ω + ω² = 0 and ω³ = 1
Now 1 – ω⁴ = 1 – (ω³) ω
= 1 – 1 (ω)
= 1 – ω
1 – ω⁸ = 1 – (ω³)² ω²
= 1 – (1) ω²
= 1 – ω²
∴ (1 – ω) (1 – ω²) (1 – ω⁴) (1 – ω⁸)
= (1 – ω) (1 – ω²)(1 – ω) (1 – ω²)
= [(1 – ω) (1 – ω²)]²
= (1 – ω – ω² + ω³)²
= [1 – (ω + ω²) + 1]² (∵ 1 + ω + ω² = 0)
= [1 – (-1) + 1]²
= (3)²
= 9
∴ (1 – ω) (1 – ω²) (1 – ω⁴) (1 – ω⁸) = 9

Question 4.
For what values of x, the expression x² – 5x + 14 is positive?
Solution:
Here a = 1, b = -5, c = 14
∆ = b² – 4ac
= 25 – 56
= -31 < 0
∴ ∆ < 0 ∵ a = 1 > 0 and ∆ < 0
⇒ x² – 5x + 14 is positive ∀ x ∈ R.

Question 5.
If α, β, γ are the roots of 4x³ – 6x² + 7x + 3 = 0, then find the value of αβ + βγ + γα.
Solution:
α, β, γ are the roots of 4x³ – 6x² + 7x + 3 = 0
α + β + γ = \(-\frac{a_1}{a_0}=\frac{6}{4}\)
αβ + βγ + γα = \(\frac{a_2}{a_0}=\frac{7}{4}\)
αβγ = \(-\frac{a_3}{a_0}=-\frac{3}{4}\)
∴ αβ + βγ + γα = \(\frac{7}{4}\)

Question 6.
Find the number of 4-digit numbers that can be formed using the digits 1, 2, 3, 4, 5, 6 that are divisible by 2.
Solution:

Take 4 blank places. First, the unit place can be filled by an even digit in 3 ways (2 or 4, or 6).
The remaining three places can be filled with the 6 digits in 6 ways each.
Thus they can be filled in 6 × 6 × 6 = 6³ ways.
Therefore, the number of 4 digited numbers divisible by 2 is 3 × 6³ = 3 × 216 = 648

Question 7.
Find the number of ways of arranging 4 boys and 3 girls around a circle so that all the girls sit together.
Solution:
Treat all the 3 girls as one unit. Then We have 4 boys and 1 unit of girls. They can be arranged around a circle in 4! ways.
Now, the 3 girls can be arranged among themselves in 3! ways.
∴ The number of required arrangements = 4! × 3!
= 24 × 6
= 144

Question 8.
Find the term independent of x in the expansion of \(\left(4 x^3+\frac{7}{x^2}\right)^{14}\).
Solution:
The general term in \(\left(4 x^3+\frac{7}{x^2}\right)^{14}\) is

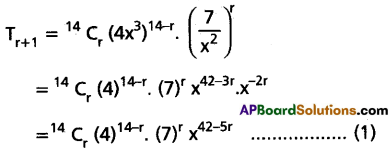
For term independent of x, put 42 – 5r = 0
⇒ r = \(\frac{42}{5}\) which is not an integer.
Hence term independent of x in the given expansion is zero.

Question 9.
Find the variance of the following data 5, 12, 3, 18, 6, 8, 2, 10.
Solution:

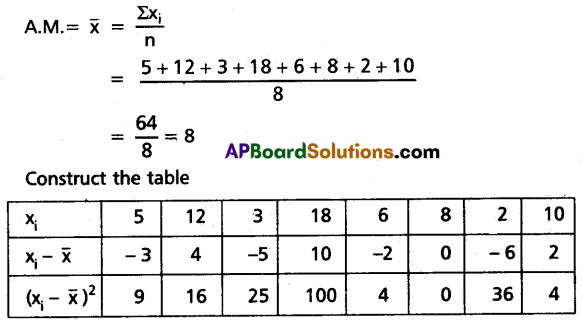
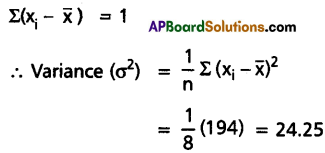
Question 10.
The probability that a person chosen at random is left-handed (in handwriting) is 0.1. What is the probability that in a group of 10 people, there is one who is left-handed?
Solution:
Here n = 10, p = \(\frac{1}{10}\) = 0.1 and q = 0.9
We have to find P(X = 1)
the probability that exactly one out of 10 is left-handed
P(X = 1) = ¹⁰C₁ p¹ q^10-1
= 10 × 0.1 × (0.9)⁹
= (0.9)⁹

Section – B
(5 × 4 = 20 Marks)

II. Short Answer Type Questions.

• Answer any five Questions.
• Each Question carries 4 marks.

Question 11.
Find the real values of x and y if \(\frac{x-1}{3+i}-\frac{y-1}{3-i}=i\).
Solution:
Given \(\frac{x-1}{3+i}-\frac{y-1}{3-i}=i\)
⇒ \(\frac{(x-1)(3-i)+(y-1)(3+i)}{9-i^2}\) = i
⇒ 3x – xi – 3 + i + 3y – iy – 3 – i = 10i
⇒ (3x + 3y – 6) + i(-x + y) = 0 + 10i
Now equating real and imaginary parts.
3x + 3y – 6 = 0
⇒ x + y- 2 = 0 …….(1)
-x + y = 10
⇒ x – y + 10 = 0 ……..(2)
(1)+(2) ⇒ 2x + 8 = 0
⇒ x = -4
From (1), -4 + y – 2 = 0
⇒ y = 6
∴ x = -4, y = 6

Question 12.
Find the changes in the sign of 4x – 5x² + 2 for x ∈ R and find the extreme value.
Solution:
The roots of 4x – 5x² + 2 = 0
⇒ 5x² – 4x – 2 = 0
Roots are \(\frac{2 \pm \sqrt{14}}{5}\)
∴ \(\frac{2-\sqrt{14}}{5}\) < x < \(\frac{2+\sqrt{14}}{5}\) sign of 4x – 5x² + 2 is positive.
x < \(\frac{2-\sqrt{14}}{5}\) or x > \(\frac{2+\sqrt{14}}{5}\), the sign of 4x – 5x² + 2 is negative.
Since a = -5 < 0, then
Maximum value = \(\frac{4 a c-b^2}{4 a}=\frac{4(-5)(2)-(4)^2}{4(-5)}=\frac{-56}{-20}=\frac{14}{5}\)
Hence extreme value = \(\frac{14}{5}\)

Question 13.
Find the number of 4-digit numbers that can be formed using the digits 2, 3, 5, 6, 8 (without repetition). How many of them are divisible by (i) 2 (ii) 3.
Solution:
The number of 4-digit numbers that can be formed using the 5-digits 2, 3, 5, 6, 8 is ⁵P₄ = 120
(i) Divisible by 2: For a number to be divisible by 2, the unit’s place should be filled with an even digit. This can be done in 3 ways (2 or 6 or 8).

Now, the remaining 3 places can be filled with the remaining 4 digits in ⁴P₃ = 24 ways.
Hence the number of 4-digit numbers divisible by 2 is 3 × 24 = 72

(ii) Divisible by 3: A number is divisible by 3 if the sum of the digits in it is a multiple of 3.
Since the sum of the given 5 digits is 24, we have to leave either 3 or 6 and use the digits 2, 5, 6, 8 or 2, 3, 5, 8.
In each case, we can permute them in 4! ways. Thus the number of 4-digit numbers divisible by 3 is 2 × 4! = 48

Question 14.
Find the number of 5-letter words that can be formed using the letters of the word NATURE that begin with ‘N’ when repetition is allowed.
Solution:
First, we can fill up the first place with N in one way.

The remaining 4 places can be filled with any one of the 6 letters in 6 × 6 × 6 × 6 = 6⁴ ways.
∴ The number of 5-letter words that can be formed using the letters of the word NATURE that begin with N when repetition is allowed = 1 × 6⁴ = 1296

Question 15.
Resolve \(\frac{x^3+x^2+1}{\left(x^2+2\right)\left(x^2+3\right)}\) into partial fractions.
Solution:
Let \(\frac{x^3+x^2+1}{\left(x^2+2\right)\left(x^2+3\right)}=\frac{A x+B}{x^2+2}+\frac{C x+D}{x^2+3}\) = \(\frac{(A x+B)\left(x^2+3\right)}{\left(x^2+2\right)}+\frac{(C x+D)\left(x^2+2\right)}{\left(x^2+3\right)}\)
∴ x³ + x² + 1 = (Ax + B) (x² + 3) + (Cx + D) (x² + 2) ………(1)
⇒ x³ + x² + 1 = (A + C)x³ + (B + D)x² + (3A + 2C)x + (3B + 2D)
Comparing the coefficients of x³, x², x and constant terms
A + C = 1, B + D = 1, 3A + 2C = 0, 3B + 2D = 1
Solve 3A + 2C = 0 & 2A + 2C = 2
∴ A = -2, C = 3
Solve 3B + 2D = 1 & 2B + 2D = 2
∴ B = – 1, D = 2
∴ \(\frac{x^3+x^2+1}{\left(x^2+2\right)\left(x^2+3\right)}=\frac{-2 x-1}{x^2+2}+\frac{3 x+2}{x^2+3}=\frac{3 x+2}{x^2+3}-\frac{(2 x+1)}{x^2+2}\)

Question 16.
Three screws are drawn at random from a slot of 50 screws, 5 of which are defective. Find the probability of the event that all 3 screws are non-defective, assuming that the drawing is (a) with replacement and (b) without replacement.
Solution:
Let S be the sample space
∴ The total number of screws = 50
The number of defective screws is 5 and the remaining 45 screws are non-defective.
Let A be the event of getting a drawing of the 3 screws that are non-defective.
(a) With Replacement

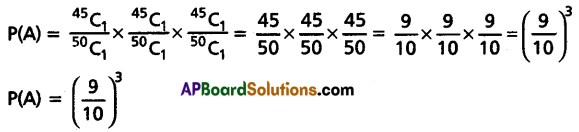
(b) Without Replacement

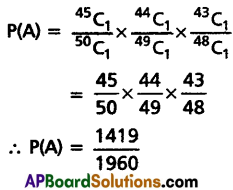
Question 17.
A Bag contains 4 red, 5 black, and 6 blue balls. Find the probability that two balls drawn at random simultaneously from the bag are a red and a black ball.
Solution:
Total number of balls in the bag = 4 + 5 + 6 = 15
From out of these balls, two balls can be drawn in ¹⁵C₂ = \(\frac{15 \times 14}{2}\) = 105 ways.
Out of 4 Red balls, one ball can be drawn in ⁴C₁ = 4 ways,
and out of 5 black balls, one ball can be drawn in ⁵C₁ = 5 ways.
If E is the event of getting a red and a black ball in a draw,
the number of cases favourable to E = 4 × 5 = 20
∴ The required probability is \(\frac{20}{105}=\frac{4}{21}\)

Section – C
(5 × 7 = 35 Marks)

III. Long Answer Type Questions.

• Answer any five Questions.
• Each Question carries 7 marks.

Question 18.
If 1, ω, ω² are the cube roots of unity, then find the value of (a + b)³ + (aω + bω²)³ + (aω² + bω)³
Solution:
Since 1, ω, ω² are the cube root of unity.
⇒ 1 + ω + ω² = 0 and ω³ = 1
Now (a + b)³ = a³ + 3a²b + 3ab² + b³ ………(1)
(aω + bω²)³ = [ω(a + bω)]³
= ω³ (a + bω)³
= (1) (a + bω)³
= a³ + 3a²bω + 3ab²ω² + b³ω³
= a³ + 3a²bω + 3ab²ω² + b³ ……..(2)
and (aω² + bω)³ = [ω(aω + b)]³
= ω³ (aω + b)³
= (1) (aω + b)³
= a³ω³ + 3a²bω³ + 3ab²ω + b³
= a³ (1) + 3a²bω² + 3ab²ω + b³
∴ (aω² + bω)³ = a³ + 3a²bω² + 3ab²ω + b³ ………(3)
adding (1), (2) & (3)
(a + b)³ + (aω + bω²)³ + (aω² + bω)³ = 3a³ + 3a²b(1 + ω + ω²) + 3ab² (1 + ω + ω²) + 3b³
= 3(a³ + b³) + 3a²b (0) + 3ab² (0)
= 3(a³ + b³)
∴ (a + b)³ + (aω + bω²)³ + (aω² + bω)³ = 3(a³ + b³)

Question 19.
Solve 3x⁴ + 16x³ + 24x² – 16 = 0, given that it has multiple roots.
Solution:
Let f(x) = 3x⁴ + 16x³ + 24x² – 16
f'(x) = 12x³ + 48x² + 48x
= 12x(x² + 4x + 4)
= 12x(x + 2)²
f”(-2) = 0
f(-2) = 3(16) + 16(-8) + 24(4) – 16 = 0
∴ x + 2 is a factor of f'(x) and f(x)
∴ -2 is multiple root of f(x) = 0

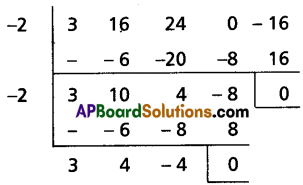
3x² + 4x – 4 = 0
⇒ 3x² + 6x – 2x – 4 = 0
⇒ 3x(x + 2) – 2(x + 2) = 0
⇒ (x + 2) (3x – 2) = 0
⇒ x = -2, \(\frac{2}{3}\)
∴ The roots of the given equation are -2, -2, -2, \(\frac{2}{3}\)

Question 20.
Find the co-efficient of x⁸ in \(\frac{(1-x)^2}{\left(1-\frac{2}{3} x\right)^3}\).
Solution:

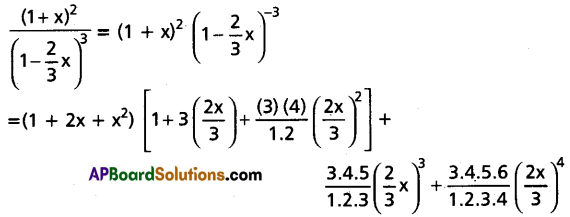
Question 21.
Prove that \(\frac{C_1}{2}+\frac{C_3}{4}+\frac{C_5}{6}+\frac{C_7}{8}+\ldots \ldots=\frac{2^n-1}{n+1}\).
Solution:

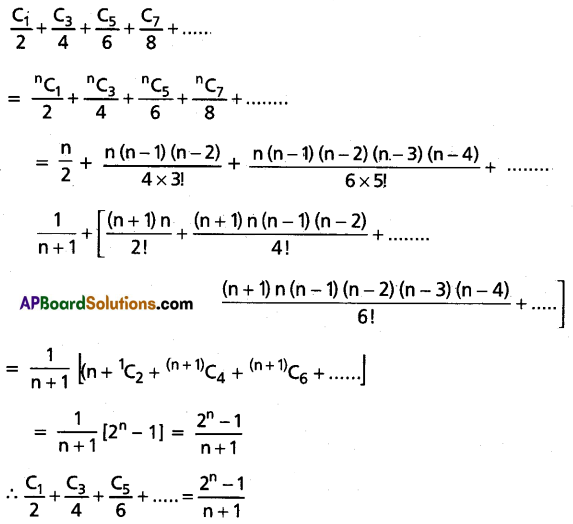
Question 22.
The following table gives the daily wages of workers. Compute the standard deviation and the coefficient of variance of the wages of the workers.

Wages (Rs.)	125-175	175-225	225-275	275-325	325-375	375-425	425-475	475-525	525-575
Number of Workers	2	22	19	14	3	4	6	1	1

Solution:
To solve this problem using the step deviation method.
Here h = 50
Let Assumed mean A = 300 Then y_i = \(\frac{x_i-300}{50}\)
Construct Table:

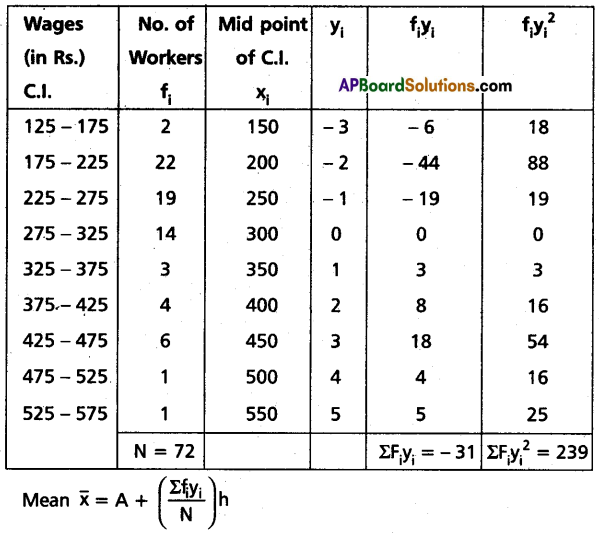
Question 23.
In a certain college, 25% of the boys and 10% of the girls are studying mathematics. The girls constitute 60% of the student’s strength. If a student selected at random is found studying mathematics, find the probability that the student is a girl.
Solution:
The probability that a student selects to be a girl
P(G) = \(\frac{60}{100}=\frac{6}{10}\)
The probability that a student selects to be a boy
P(B) = \(\frac{40}{100}=\frac{4}{10}\)
The probability that a boy studying mathematics
P(M/B) = \(\frac{25}{100}=\frac{1}{4}\)
Similarly, the probability that a girl studying mathematics
P(M/G) = \(\frac{10}{100}=\frac{1}{10}\)
We have to find P(G/M)
By Baye’s theorem

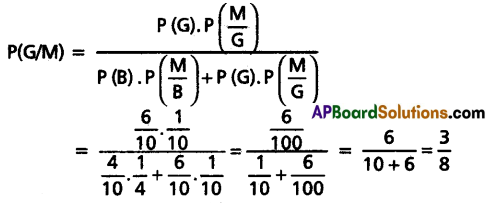
Question 24.

X = x	-2	-1	0	1	2	3
P(X = x)	0.1	K	0.2	2K	0.3	K

is the probability distribution of a random variable X. Find the value of K and the variance of X.
Solution:
The Sum of the probabilities = 1
⇒ 0.1 + K + 0.2 + 2K + 0.3 + K = 1
⇒ 4K + 0.6 = 1
⇒ 4K = 1 – 0.6 = 0.4
⇒ K = \(\frac{0.4}{4}\) = 0.1
Mean = (-2) (0.1) + (-1) K + 0 (0.2) + 1 (2K) + 2 (0.3) + 3K
= -0.2 – K + 0 + 2K + 0.6 + 3K
= 4K + 0.4
= 4(0.1) + 0.4
= 0.4 + 0.4
= 0.8
∴ µ = 0.8
Variance (σ²) = \(\sum_{i=1}^n x_i^2 P\left(x=x_i\right)-\mu^2\)
Variance = 4 (0.1) + 1 (K) + 0 (0.2) + 1 (2K) + 4 (0.3) + 9K – µ²
= 0.4 + K + 0 + 2K + 4(0.3) + 9K – (0.8)²
= 12K + 0.4 + 1.2 – (0.8)²
= 12(0.1) + 1.6 – 0.64
= 1.2 + 1.6 – 0.64
= 2.8 – 0.64
= 2.16
∴ σ² = 2.16