AP Inter 2nd Year Maths 2A Model Paper Set 1 with Solutions

Thoroughly analyzing AP Inter 2nd Year Maths 2A Model Papers Set 1 helps students identify their strengths and weaknesses.

AP Inter 2nd Year Maths 2A Model Paper Set 1 with Solutions

Time: 3 Hours
Maximum Marks: 75

Note: This Question Paper consists of three sections A, B, and C.

Section – A
(10 × 2 = 20 Marks)

I. Very Short Answer type Questions.

• Answer all Questions.
• Each Question carries 2 marks.

Question 1.
Find the square root of 7 + 24i.
Solution:

Question 2.
If x + iy = cis α . cis β, then find the value of x² + y².
Solution:
Given x + iy = cis α . cis β
⇒ x + iy = (cos α + i sin α) (cos β + i sin β)
⇒ x + iy = cos (α + β) + i sin (α + β)
Equating real arid imaginary parts
x = cos (α + β) and y = sin (α + β)
∴ x² + y² = cos²(α + β) + sin²(α + β) = 1

Question 3.
Find the value of (1 + i√3)³.
Solution:
Let 1 + i√3 = r (cos θ + i sin θ)
Equating real and imaginary parts
r cos θ = 1 and r sin θ = √3
⇒ r² (1) = 1 + 3 = 4
⇒ r = 2
∴ cos θ = \(\frac{1}{2}\) and sin θ = \(\frac{\sqrt{3}}{2}\) ⇒ θ = \(\frac{\pi}{3}\)
1 + i√3 = (2) [cos \(\frac{\pi}{3}\) + i sin \(\frac{\pi}{3}\)]
(1 + i√3)³ = (2)³ [cos \(\frac{\pi}{3}\) + i sin \(\frac{\pi}{3}\)]³
= 8[cos 3(\(\frac{\pi}{3}\)) + i sin 3(\(\frac{\pi}{3}\))]
= 8[cos π + i sin π]
= 8(-1)
= -8

Question 4.
Solve x² – 4x – 21 ≥ 0 by algebraic method.
Solution:
x² – 4x – 21 ≥ 0
⇒ x² – 7x + 3x – 21 ≥ 0
⇒ x(x – 7) + 3(x – 7) ≥ 0
⇒ (x + 3) (x – 7) ≥ 0
Co-efficient of x² = 1 > 0,
The given expression is ≥ 0
x does not lie between -3 and 7
i.e., {x / x ∈ (-∞, -3) ∪ [7, ∞)}

Question 5.
If α, β, γ are the roots of x³ + px² + qx + r = 0, then find \(\Sigma \frac{1}{\alpha^2 \beta^2}\).
Solution:

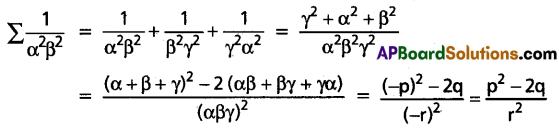
Question 6.
Find the number of ways of arranging the letters of the word a⁴b³c⁵ in its expanded form.
Solution:
The expanded form a⁴b³c⁵ is aaaa bbb ccccc.
This word has 12 letters of which there are 4a’s, 3b’s, and 5c’s.
We know that the number of linear permutations of n things in which p like things of one, q like things of second, and r like things of the third kind is \(\frac{n !}{p ! q ! r !}=\frac{12 !}{4 ! 3 ! 5 !}\)

Question 7.
If ¹²C_r = 495, find the possible values of r.
Solution:

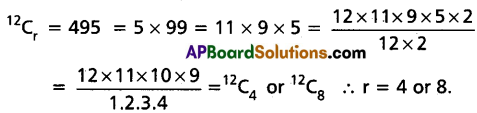
Question 8.
Find the coefficient of x¹⁰ in the expansion of \(\frac{1+2 x}{(1-2 x)^2}\).
Solution:
\(\frac{1+2 x}{(1-2 x)^2}\) = (1 + 2x) (1 – 2x)^-2
= (1 + 2x) [1 + 2(2x) + 3(2x)² + 4(2x)³ + 5(2x)⁴ + 6(2x)⁵ + 7(2x)⁶ + 8(2x)⁷ + 9(2x)⁸ + 10(2x)⁹ + 11 (2x)¹⁰ + …… + (r – 1).(2x)^r + ……]
∴ The coefficient of x¹⁰ in \(\frac{1+2 x}{(1-2 x)^2}\) is (11) (2)¹⁰ + 10 (2) (2)⁹
= 2¹⁰ (11 + 10)
= 21 × 2¹⁰

Question 9.
The coefficient of variation of two distributions are 60 and 70 and their standard deviations are 21 and 16 respectively. Find their arithmetic means.
Solution:
Given the co-efficient of variance C.V. = 60
Standard deviation σ = 21
We know C.V. = \(\frac{\sigma}{\bar{x}} \times 100\)
⇒ \(\overline{\mathrm{x}}=\frac{\sigma}{\mathrm{C} . \mathrm{V} .} \times 100\)
= \(\frac{21}{60}\) × 100
= 35
Arithmetic mean = 35
Given the co-efficient of variance C.V. = 70
Standard deviation σ = 16
We know CV. = \(\frac{\sigma}{\bar{x}} \times 100\)
⇒ \(\overline{\mathrm{x}}=\frac{\sigma}{\mathrm{C} . \mathrm{V} .} \times 100\)
= \(\frac{16}{70}\) × 100
= 22.85

Question 10.
A Poisson variable satisfies P(X = 1) = P(X = 2). Find P(X = 5).
Solution:
We have P(X = r) = \(\frac{e^{-\lambda} \lambda^r}{r !}\), λ > 0
Given that P(X = 1) = P(X = 2)
⇒ \(\frac{\lambda \mathrm{e}^{-\lambda}}{1 !}=\frac{\lambda^2 \mathrm{e}^{-\lambda}}{2 !}\)
⇒ λ² = 2λ
⇒ λ(λ – 2) = 0
∴ λ = 2 (since λ > 0)
Hence P(X = 5) = \(\frac{e^{-2} 2^5}{5 !}\)

Section – B
(5 × 4 = 20 Marks)

II. Short Answer Type Questions.

• Answer any five Questions.
• Each Question carries 4 marks.

Question 11.
Express the 1 – i in modulus-amplitude form.
Solution:
Let 1 – i = r (cos θ + i sin θ)
Equating real and imaginary parts,
r cos θ = 1
r sin θ = -1
⇒ θ lies in IV Quadrant.
Squaring and Adding
r² (cos²θ + sin²θ) = 1 + 1 = 2
⇒ r² = 2
⇒ r = √2
tan θ = -1
⇒ θ = \(-\frac{\pi}{4}\)
∴ 1 – i = \(\sqrt{2}\left[\cos \left(-\frac{\pi}{4}\right)+i \sin \left(-\frac{\pi}{4}\right)\right]\)

Question 12.
Find the range of \(\frac{2 x^2-6 x+5}{x^2-3 x+2}\).
Solution:
y = \(\frac{2 x^2-6 x+5}{x^2-3 x+2}\)
⇒ yx² – 3yx + 2y = 2x² – 6x + 5
⇒ (y – 2)x² + (6 – 3y)x + (2y – 5) = 0
x ∈ R ⇒ (6 – 3y)² – 4(y – 2) (2y – 5) ≥ 0
⇒ 36 + 9y² – 36y – 4(2y² – 9y + 10) ≥ 0
⇒ 36 + 9y² – 36y – 8y² + 36y – 40 ≥ 0
⇒ y² – 4 ≥ 0
⇒ y² – 4 = 0
⇒ y² = 4
⇒ y = ±2
y² – 4 ≥ 0
⇒ y ≤ -2 or y ≥ 2
⇒ y does not lie between -2, 2
∴ y² coefficient is > 0 and exp is also ≥ 0
∴ Range of \(\frac{2 x^2-6 x+5}{x^2-3 x+2}\) is (-∞, -2] ∪ [2, ∞)

Question 13.
Find the number of ways of arranging the letters of the words.
(i) PERMUTATION
(ii) COMBINATION
Solution:
(i) The word PERMUTATION contains 11 letters in which there are 2 T’s that are alike and the rest are different.
∴ The number of required arrangements = \(\frac{(11) !}{2 !}\)

(ii) The word COMBINATION contains 11 letters in which there are 2 O’s are alike, 2 I’s are alike, 2 N’s are alike and the rest are different.
∴ The number of required arrangements = \(\frac{(11) !}{2 ! 2 ! 2 !}\)

Question 14.
Find the number of numbers that are greater than 4000 which can be formed using the digits 0, 2, 4, 6, and 8 without repetition.
Solution:
While forming any digit number with the given digits, zero cannot be filled in the first place. We can fill the first place with the remaining 4 digits.
The remaining places can be filled with the remaining 4 digits.
All the numbers of 5 digits are greater than 4000. In the 4-digit numbers, the numbers starting with 4, or 6, or 8 are greater than 4000.
The number of 4 digit numbers which begin with 4 or 6 or 8 = 3 × ⁴P₃
= 3 × 24
= 72
The number of 5-digit numbers = 4 × 4!
= 4 × 24
= 96
The number of numbers greater than 4000 is 72 + 96 = 168

Question 15.
Resolve \(\frac{x^3}{(2 x-1)(x-1)^2}\) into partial fractions.
Solution:
Let \(\frac{x^3}{(2 x-1)(x-1)^2}=\frac{1}{2}+\frac{A}{2 x-1}+\frac{B}{x-1}+\frac{C}{(x-1)^2}\)
Multiplying with 2(2x – 1) (x – 1)²
2x³ = (2x – 1) (x – 1)² + 2A(x – 1)² + 2B(2x – 1) (x – 1) + 2C(2x – 1)
Put x = \(\frac{1}{2}\),
2(\(\frac{1}{8}\)) = 2A(\(\frac{1}{4}\))
⇒ A = \(\frac{1}{2}\)
Put x = 1,
2(1) = 2C(1)
⇒ C = 1
Put x = 0,
0 = (-1) (1) + 2A(1) + 2B(-1) (-1) + 2C(-1)
⇒ 2A + 2B – 2C = 1
⇒ 2B = 1 + 2C – 2A
⇒ B = 1 + 2 – 1
⇒ B = 1
∴ \(\frac{x^3}{(2 x-1)(x-1)^2}=\frac{1}{2}+\frac{1}{2(2 x-1)}+\frac{1}{(x-1)}+\frac{1}{(x-1)^2}\)

Question 16.
Two squares are chosen at random on a chessboard. Show that the probability that they have a side in common is \(\frac{1}{18}\).
Solution:
The number of ways of choosing the first square is 64 and that of the second is 63.
∴ The number of ways of choosing the first and second squares = 64 × 63
∴ n(S) = 64 × 63
Let E be the event that these squares have a side in common.
If the first square happens to be one of the squares in the four corners of the chess board, the second square (with a common side) can be chosen in 2 ways.
If the first square happens to be any one of the remaining 24 squares along the four sides of the chess board other than the comer, the second square can be choosen in 3 ways.
If the first square happens to be any one of the remaining 36 inner squares, then the second square can be choosen in 4 ways.
Hence the number of cases favourable to E is (4 × 2) + (24 × 3) + (36 × 4) = 224
∴ The required probability = \(\frac{n(E)}{n(S)}=\frac{224}{64 \times 63}=\frac{1}{18}\)

Question 17.
If A and B are two events then show that
(i) P(A ∩ B^C) = P(A) – P(A ∩ B)
(ii) The probability that one of them occurs is given by P(A) + P(B) – 2P(A ∩ B)
Solution:
(i) We have A = (A ∩ B) ∪ (A ∩ B^C) and (A ∩ B) ∩ (A ∩ B^C) = φ
Hence P(A) = P(A ∩ B) + P (A ∩ B^C)
∴ P(A ∩ B^C) = P(A) – P(A ∩ B)

(ii) Let E be the event that exactly one of them, i.e., either A or B occurs.
Then, E = (A – B) ∪ (B – A) = (A ∩ B^C) ∪ (B ∩ A^C)
So, P(E) = P(A ∩ B^C) + P (B ∩ A^C) (Since (A ∩ B^C) ∩ (B ∩ A^C) = φ)
= P(A) – P(A ∩ B) + P(B) – P(B ∩ A) (∵ Using (i))
= P(A) + P(B) – 2P(A ∩ B)

Section – C
(5 × 7 = 35 Marks)

III. Long Answer Type Questions.

• Answer any five Questions.
• Each Question carries 7 marks.

Question 18.
Find the common roots of x¹² – 1 = 0 and x⁴ + x² + 1 = 0.
Solution:
Consider x¹² – 1 = 0
⇒ x¹² = 1
⇒ x¹² = (cos 0 + i sin 0)
⇒ x¹² = (cos 2kπ + i sin 2kπ), k is a positive integer.
⇒ x = (cos 2kπ + i sin 2kπ)^1/12
⇒ x = cis \(\frac{2 \mathrm{k} \pi}{12}\)
⇒ x = cis \(\frac{k \pi}{6}\), k = 0, 1, 2, 3, …….., 11

Question 19.
Find the roots of x⁴ – 16x³ + 86x² – 176x + 105 = 0.
Solution:
Let f(x) = x⁴ – 16x³ + 86x² – 176x + 105
Now f(1) = 1 – 16 + 86 – 176 + 105 = 0
∴ 1 is a root of f(x) = 0
⇒ x – 1 is a factor of f(x)

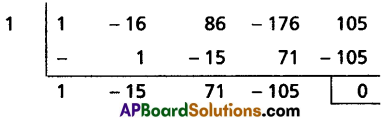
∴ f(x) = (x – 1) (x³ + 15x² + 71x – 105)
= (x – 1) g(x)
where g(x) = x³ – 15x² + 71x – 105
g(1) = 1 – 15 + 71 – 105 = -48 ≠ 0
g(2) = -15 ≠ 0
g(3) = 27 – 135 + 213 – 105 = 0
∴ 3 is a root of g(x) = 0
⇒ x – 3 is a factor of g(x)

∴ g(x) = (x – 3) (x² – 12x + 35) = (x – 3) (x – 5) (x – 7)
∴ f(x) = (x – 1) (x – 3) (x – 5) (x – 7)
∴ 1, 3, 5, 7 are the roots of f(x) = 0.

Question 20.
Find the numerically greatest term in the expansion of (4 + 3x)¹⁵ when x = \(\frac{7}{2}\).
Solution:

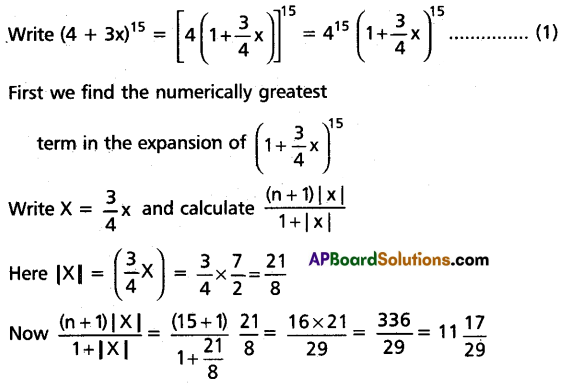
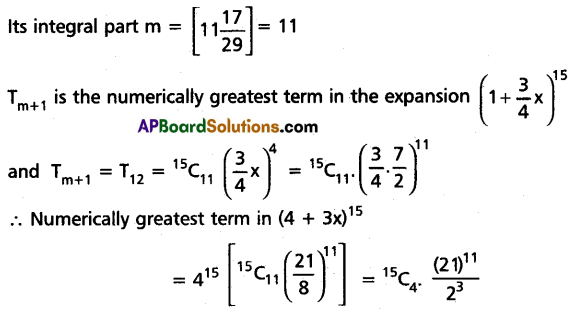
Question 21.
If n is a positive integer, prove that \(\sum_{r=1}^n r^3 \cdot\left(\frac{{ }^n C_T}{{ }^n C_{T-1}}\right)^2=\frac{n(n+1)^2(n+2)}{12}\).
Solution:

Question 22.
The scores of two cricketers A and B in 10 innings are given below. Find who is a better run-getter and who is a more consistent player.

Scores of A: xi	40	25	19	80	38	8	67	121	66	76
Scores of B: yi	28	70	31	0	14	111	66	31	25	4

Solution:



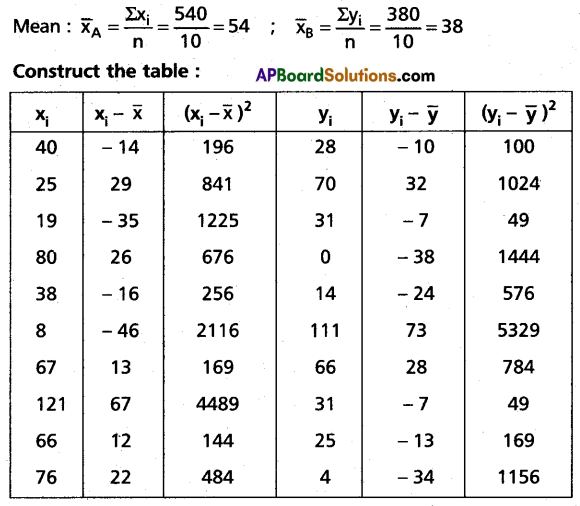
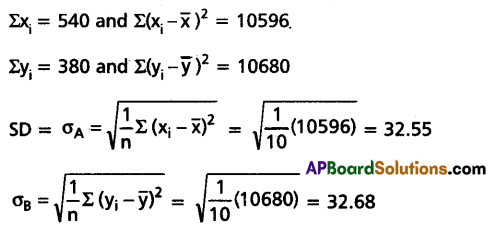
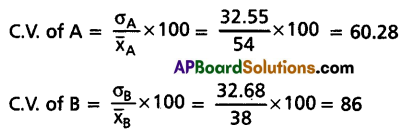
Since \(\bar{x}_A>\bar{x}_B\)
∴ Cricketer A is a better run-getter.
Since C.V. of A < C.V. of B.
Hence Cricketer A is a more consistent player.

Question 23.
A, B, and C are 3 Newspapers from a city. 20% of the population read A, 16% read B, 14% read C, 8% both A and B, 5% read Both A and C, 4% read both B and C and 2% all three. Find the percentage of the population who read atleast one newspaper.
Solution:

Given P(A) = \(\frac{20}{100}\) = 0.2
P(B) = \(\frac{16}{100}\) = 0.16
P(C) = \(\frac{14}{100}\) = 0.14
P(A ∩ B) = \(\frac{8}{100}\) = 0.08
P(B ∩ C) = \(\frac{4}{100}\) = 0.04
P(A ∩ C) = \(\frac{5}{100}\) = 0.05
P(A ∩ B ∩ C) = \(\frac{2}{100}\) = 0.02
P(A ∪ B ∪ C) = P(A) + P(B) + P(C) – P(A ∩ B) – P(B ∩ C) – P(C ∩ A) + P(A ∩ B ∩ C)
= 0.2 + 0.16 + 0.14 – 0.08 – 0.04 – 0.05 + 0.02
= 0.52 – 0.17
= 0.35
Percentage of the population who read atleast one newspaper = 0.35 × 100 = 35%

Question 24.
A cubical die is thrown. Find the mean and variance of X, giving the number on the face that shows up.
Solution:
Let S be the sample space and X be the random variable associated with S, where the following table gives P(X).