AP Inter 1st Year Physics Question Paper May 2019

Thoroughly analyzing AP Inter 1st Year Physics Model Papers and AP Inter 1st Year Physics Question Paper May 2019 helps students identify their strengths and weaknesses.

AP Inter 1st Year Physics Question Paper May 2019

Time: 3 Hours
Maximum Marks: 60

Section – A (10 × 2 = 20)

Note :

• Answer all questions.
• Each question carries two marks.
• All are very short answer type questions.

Question 1.
What are are the fundamental forces in nature ?
Answer:
The four fundamental forces in nature are :

1. Gravitational force
2. Electromagnetic force
3. Strong nuclear force
4. Weak nuclear force.

Question 2.
The error in measurement of radius of sphere is 1 %. What is the error in the measurement of volume ?
Answer:
Radius of the sphere
\(\frac{\Delta r}{r}\) × 100 = 1%
Volume (V) = \(\frac{4}{8}\) πr³
⇒ \(\frac{\Delta \mathrm{V}}{\mathrm{V}}\) × 100 = 3 × \(\frac{\Delta r}{r}\) × 100
= 3 × 1%
= 3%.

Question 3.
What is the acceleration of projectile at the top of its trajectory ?
Answer:
The acceleration of a projectile at the top of its trajector is vertically downwards.

Question 4.
What happens to the coefficient of frictions if the weight of the body is doubled ?
Answer:
If the weight of a body is doubled, coefficient friction does not change. Coefficient of friction is independent of normal reaction.

Question 5.
Given the expression for the excess pressure in a soap bubble in air.
Answer:
Soap bubble have two interfaces, hence excess pressure inside a soap bubble is P_i – P_o = \(\frac{4 s}{r}\)
Where S = Surface tension
r = Radius of soap bubble.

Question 6.
What is the principle behind the carburetor of an automobile ?
Answer:
The carburetor of automobile has a venturi channel (nozzle) through which air flows with a large speed. The pressure is then lowered at the narrow neck and the petrol is sucked up in the chamber to provide the correct mixture of air to fuel necessary for combustion.

Question 7.
State Wien’s displacement law.
Answer:
The wavelength (λm) corresponding to maximum energy emitted by a black body is inversely proportional to its absolute temperature (T).
i.e., λ_m ∝ \(\frac{1}{\mathrm{~T}}\)

Question 8.
Why gaps are left between rails on a railway track ?
Answer:
The length of the rails increases in summer due to high temperature. Therefore a gap is left to allow this expansion.

Question 9.
Define mean free path.
Answer:
The average distance covered by a molecule between two successive collision is called the mean free path.

Question 10.
The absolute temperature of a gas is increased 3 times. What will be increase in rms velocity of the gas molecule ?
Answer:
V_rms = \(\sqrt{\frac{3 R T}{M}}\)
⇒ V ∝ √T
⇒ \(\frac{V_2}{V_1}=\sqrt{\frac{T_2}{T_1}}=\sqrt{\frac{3 T_1}{T_1}}\) = √3
⇒ V₂ = √3 V₁ = 1.732 V₁
Increase in r.m.s velocity = V₂ – V₁ = 1.732 V₁ – V₁ = 0.732 VV₁.

Section – B (6 × 4 = 24)

Note :

• Answer any six of the following questions.
• Each question carries four marks.
• All are short answer type questions.

Question 11.
Show that the maximum height reached by a projectile launched at an angle 45° is one quarter of the range.
Answer:
The horizontal distance travelled by a projectile during its time of flight is called Range.
We know that Range R = \(\frac{u^2 \sin 2 \theta}{g}\) and maximum height
h = \(\frac{u^2 \sin ^2 \theta}{2 g}\)
It is clear that R is maximum, when θ = 45°
Maximum height H_max = \(\frac{u^2 \sin ^2 \theta}{2 g}\) = \(\frac{u^2}{2 g}\)(sin 45°)
= \(\frac{u^2}{2 g}\)(\(\frac{1}{\sqrt{2}}\))² = \(\frac{u^2}{4 g}\) ………. (1)
Maximum Range R_max = \(\frac{u^2}{g}\) sin 2θ = \(\frac{u^2}{g}\) sin 90° = \(\frac{u^2}{g}\) ………. (2)
∴ From (1) & (2), H_max = \(\frac{R_{\text {max }}}{4}\)
Thus, maximum Height is one quarter of the Range.

Question 12.
If |\(\overline{\mathbf{a}}\) + \(\overline{\mathbf{b}}\)| = |\(\overline{\mathbf{a}}\) – \(\overline{\mathbf{b}}\)| I prove that the angle between a and b is 90°.
Solution:
Given, |\(\overline{\mathbf{a}}\) + \(\overline{\mathbf{b}}\)| and |\(\overline{\mathbf{a}}\) – \(\overline{\mathbf{b}}\)|
⇒ \(\sqrt{a^2+b^2+2 a b \cos \theta}\) = \(\sqrt{a^2+b^2-2 a b \cos \theta}\)
Squaring on both sides
⇒ a² + b² + 2ab cos θ = a² + b² – 2ab cos θ
⇒ 2ab cos θ = – 2 ab cos0
⇒ 4 ab cos θ = 0
⇒ cos θ = 0
⇒ cos θ = cos 90°
⇒ θ = 90°

Question 13.
Explain the advantages and disadvantages of friction.
Answer:
Advantages :

1. We cannot walk without friction between feet and ground.
2. ‘Brakes’ are able to stop the vehicles only due to friction between brake shoes and the inner surface of the brake drum.
3. We are able to pick up a Book only because of friction between Hand and the Book.
4. In a Machine, power is transmitted from the Motor to different parts of the Machine only by using friction between the Belt and the Wheels.

Disadvantages :

1. A part of the energy delivered by the Motor is wasted to overcome friction.
2. Friction between different parts of the Machine produces uneven ‘wear and tear’ which gradually takes the Machine to a condemned stage.

Question 14.
Write equations of motion for a particle rotating about a fixed point.
Answer:
When a body is rotating with constant angular acceleration (a), the rotational kinematical equations are :
1) ω = ω₀ + αt
2) θ = ω₀t + \(\frac{1}{2}\)αt²
3) ω₂ – ω₀² = 2αθ
Where ω₀ = Initial angular velocity
ω – angular velocity after time ‘t’.
α = angular acceleration
θ = angular displacement.

Question 15.
Define angular acceleration and torque. Establish the relation between angular acceleration and torque.
Answer:
Angular acceleration (α) : The rate of change of angular velocity is called angular acceleration
α = \(\frac{\omega}{t}\) or \(\frac{\mathrm{d} \omega}{\mathrm{dt}}\)
Torque (τ) : Torque is defined as the product of force and perpendicular distance of the line of action of the force from the point.
\(\bar{\tau}\) = \(\bar{r}\) × \(\overline{\mathrm{F}}\) = rF sin θ
Relation between angular acceleration and torque :
torque (τ) = Perpendicular distance × force
⇒ \(\bar{\tau}\) = \(\bar{r}\) × \(\overline{\mathrm{F}}\) = r × ma =rm (rα)
⇒ x = mrα
∴ τ = Iα

Question 16.
Derive the relation between acceleration due to gravity (g) at the surface of a planet and Gravitational constant (G).
Answer:
Relation between g and G : Consider a body of mass ‘m’ is placed on the surface of a planet of mass. ‘M’ and radius ‘R’. The distance between the centres of the planet and the body is equal to the radius of the planet (R).
According to Newton’s law of gravitation the gravitational force on the body is
F = \(\frac{\mathrm{GMm}}{\mathrm{R}^2}\) ________ (1)
Where ‘G’ is universal gravitational constant.
The force acting on the body due to gravitational pull of the planet is F = mg ________ (2)
From equations (1) and (2), we have mg = \(\frac{\mathrm{GMm}}{\mathrm{R}^2}\)
∴ g = \(\frac{G M}{R^2}\) ________ (3)

Question 17.
Define stress and explain the types of stress.
Answer:
Stress : The restoring force per unit area is called stress
∴ Stress = \(\frac{\text { Restoring Force }}{\text { Area }}\) = \(\frac{F}{A}\)
Stress is classified into three types :
1) Longitudinal stress
2) Volume (or) Bulk stress
3) Tangential (or) shearing stress.

1. Longitudinal stress (or) Linear stress : When a normal stress changes the length of a body, then it is called longitudinal stress.
∴ Longitudinal stress = \(\frac{F}{A}\).

2. Volume (or) Bulk stress : When a normal stress changes the volume of a body, then it is called volume stress.
Volume stress = \(\frac{\text { Restoring Force }}{\text { Area }}\) = pressure.

3. Tangential (or) shearing stress : When the stress is tangential , to the surface due to the application of forces parallel to the surface, then the stress is called tangential stress.
Tangential stress = \(\frac{F}{A}\).

Question 18.
Pendulum clocks generally go fast in winter and slow in summer. Why ?
Answer:
The time period of a pendulum clock is given by
T₁ = \(2 \pi \sqrt{\frac{l}{g}}\) ⇒ T ∝ l
The pendulum of a clock expands in summer, so its time period increases. Hence, it makes less number of oscillations than required per day. Hence, it will lose time or clock goes slow. The pendulum of a clock contracts in winter, its length decreases so, its time period decreases. Hence, it makes more number of oscillations than required per day. Hence it will gain time or clock goes fast.

Section – C (2 × 8 = 16)

Note :

• Answer any two of the following questions.
• Each question carries eight marks.
• All are long answer type questions.

Question 19.
a) State and prove law of conservation of energy in case of freely falling body.
b) A machine gun fires 360 bullets per minute and each bullet travels with a velocity of 600 m/s. If the mass of each of bullet is 5 gm. Find the power of machine gun.
Answer:
a) Law of conservation of energy: Energy can neither be created nor be destroyed’.
It can be converted from one form to anothe form. (Or) Total energy remains constant in a closed system.

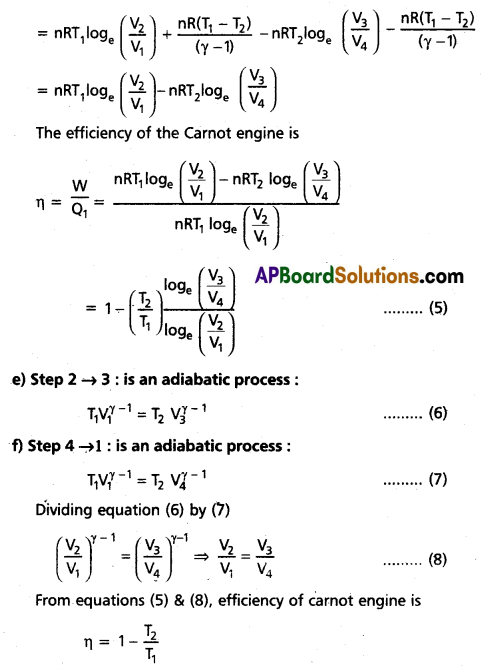
Proof : Consider a freely falling body of mass’m’ released from a point ‘A’, at a height ‘h’ above the ground, as shown in the figure.

At Point A :
Potential Energy P.E = mgh
Velocity at A is v_A = u = 0
Here, Kinetic Energy
K.E = \(\frac{1}{2} m v_A^2\) = \(\frac{1}{2}\) m(0)² = 0
∴ Total Energy
T.E = P.E + K.E
= mgh + 0 = mgh ________ (1)

At Point B :
Let the body travels a distance x and reaches the point B.
Now, the height of the body from the ground is (h – x)
∴ P.E = mg(h – x) = mgh – mgx
Also, at the point B we have s = x, u = 0, v = v_B, a = +g
∴ v² – u² = 2as ⇒ v_B² = 2gx
Here K.E = \(\frac{1}{2} m v_B^2\) = \(\frac{1}{2}\) m(2gx) = mgx
∴ T.E = P.E + K.E = mgh – mgx + mgx = mgh ________ (2)

At Point C :
Let the body hits the ground at C
At point C we have h = 0
∴ P.E = mgh = mg(0) = 0
Also, at the point C we have s = h, u = 0, v = v_c, a = +g
∴ v² – u² = 2as ⇒ v_C² = 2gh
Here K.E = \(\frac{1}{2} m v_C^2\) = \(\frac{1}{2}\)m(2gh) = mgh
∴ T.E = P.E + K.E = 0 + mgh = mgh ________ (3)
From (1), (2), (3) it is clear that the total energy T.E is always constant.
Thus, the law of conservation of energy is verified.

b) A machine gun fires 360 bullets per minute and each bullet travels with a velocity of 600 m/s. If the mass of each of bullet is 5 gm. Find the power of machine gun.
Solution:
Here, n = 360; t = 60 sec; v = 600 mts
m = 5 gm = 5 × 10^-3kg
Power, P = \(\frac{n\left(\frac{1}{2} m v^2\right)}{t}\)
⇒ P = \(\frac{\frac{1}{2} \times 5 \times 10^{-3} \times 360 \times 600 \times 600}{60}\)
⇒ P = 5400 w = 5.4 kw.

Question 20.
Derive the equation for the kinetic energy and potential energy of a simple harmonic oscillator and show that the total energy of a particle in simple harmonic motion is constant at any point on its path.
Answer:
Kinetic Energy : We know the displacement of a particle executing SHM is y = A sin ωt

∴ The kinetic energy of the particle is given by
K.E = \(\frac{1}{2}\)mv² = \(\frac{1}{2}\)mω² (A² – y²) ________ (1)

Potential energy : Potential energy of a simple harmonic oscillator is equal to the workdone against the restoring force in producing the displacement ‘y’.
Average Force = \(\frac{0+F}{2}\) = \(\frac{F}{2}\)
Workdone = Average Force displacement
⇒ ω = \(\frac{F}{2}\)y = \(\frac{(\mathrm{ma}) \mathrm{y}}{2}\) [∵ F = ma]
But a = ω²y
∴ w = \(\frac{m\left(\omega^2 y\right) y}{2}\)y = \(\frac{m \omega^2 y^2}{2}\)
This work done is equal to the Potential energy (P.E.) of the oscillator
∴ P.E = \(\frac{1}{2}\)mω²y² ________ (2)
Now, from (1) and (2);
Total Energy T.E = K.E + P.E = \(\frac{1}{2}\)mω² (A² – y²) + \(\frac{1}{2}\)mω²y²
\(\frac{1}{2}\)mω²(A² – y² + y²)
= \(\frac{1}{2}\)mω² A² constant
Thus, the total energy of simple harmonic oscillator is constant and it is independent of time and position.
Also, at mean position T.E = K.E [∵ P.E = 0] and at extreme position T.E = P.E [∵ K.E = 0]

Question 21.
Explain reversible and irreversible processes. Describe the working of Carnot engine. Obtain an expression for the efficiency.
Answer:
Reversible process : A process that can be retraced back in the opposite direction is called a reversible process.
Ex : Fusion of ice and vaporisation of water.

Irreversible process : A process that cannot be retraced back in the opposite direction is caleld an irtevesible process.
Ex : Work done against friction.

Carnot engine : A reversible heat engine operating between two temperatures is called a Carnot engine.

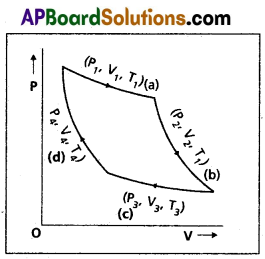
Working of Carnot engine : The carnot engine undergoes a cycle or processes called carnot cycle. It consists of two isothermal processes connected by two adiabatic processes. Ideal gas acts as the working substance in carnot erigine.

The steps of Carnot cycle:
a) Step 1 → 2 : Isothermal expansion of the gas taking its state from (P₁, V₁, T₁) to (P₂, V₂, T₁). The heat absorbed by the gas (Q₁) from the reservoir at temperature T₁ equals the work done.
W_{1 → 2} by the gas on the environment.

W_{1 → 2} = Q₁ = nRT₁ log_e (\(\frac{V_2}{V_1}\)) ……. (1)

b) Step 2 → 3 : Adiabatic expansion of the gas from (P₂, V₂, T₁) to (P₃, V₃, T₂) :
Work done by the gas is
W_{2 → 3} = \(\frac{n R\left(T_1-T_2\right)}{(\gamma-1)}\) ………… (2)

c) Step 3 → 4 : Isothermal compression of the gas from (P₃,V₃, T₂) to (P₄, V₄, T₂) : Heat released (Q₂) by the gas to the reservoir at temperature T₂ is equal to the work done on the gas by the environment.
W_{3 → 4} = Q₂ = nRT₂ log_e (\(\frac{V_3}{V_4}\)) ……. (3)

d) Step 4 → 1 : Adiabatic compression for the gas from (P₄,V₄, T₂) to (P₁, V₁ T₁) :
Work done on the gas is W_{4 → 1} = \(\frac{n R\left(T_1-T_2\right)}{(\gamma-1)}\) ………… (4)
Total workdone by the gas in one complete cycle is
W = W_{1 → 2} + W_{2 → 3} + W_{3 → 4} + W_{4 → 1}