AP Inter 1st Year Physics Question Paper April 2022

Thoroughly analyzing AP Inter 1st Year Physics Model Papers and AP Inter 1st Year Physics Question Paper April 2022 helps students identify their strengths and weaknesses.

AP Inter 1st Year Physics Question Paper April 2022

Time: 3 Hours
Maximum Marks: 60

Section – A (10 × 2 = 20)

Note :

• Answer ALL questions.
• Each Question carries TWO marks.
• ALL are very short answer type questions.

Question 1.
What is the discovery of C.V. Raman ?
Answer:
In elastic scattering of light by molecules.

Question 2.
How can systematic errors be minimised or eliminated ?
Answer:
Systematic errors can be minimised by improving experimental techniques, selecting better instruments and removing personal bias as far as possible. For a given set up, these errors may be estimated to a certain extent and the necessary corrections may be applied to the readings.

Question 3.
\(\vec{A}\) = \(\vec{i}\) + \(\vec{j}\), what is the angle between vector and X-axis ?
Answer:
\(\vec{A}\) = \(\vec{i}\) + \(\vec{j}\)
cos α = \(\frac{A x}{|A|}\) (A_x = 1)
= \(\frac{1}{\sqrt{1^2+1^2}}\) = \(\frac{1}{2}\)
α cos^-1 (\(\frac{1}{2}\)) = 45°

Question 4.
A horse has to pull harder during the start of the motion than latter. Explain.
Answer:
We know the limiting frictional force is greater than kinetic frictional force. For starting motion of the cart, the limiting friction is to be overcome. Once motion is set, frictional force reduces. Therefore, the horse has to pull harder during starting of the cart.

Question 5.
Define average pressure. Is it a scalar or a vector ?
Answer:
Average pressure (P_av): Average power is defined as the normal force acting per unit area.
P_av = \(\frac{F}{A}\)
units → N / m² (or) pascal
Dimensional formula → [ML^-1 T^-1]
Pressure is a scalar quantity.

Question 6.
Why liquid drops and bubbles are spherical ?
Answer:
The surface tension of a liquid tends to have minimum surface area. For a given volume, the surface area is minimum for a sphere. Hence rain drops are spherical shape.

Question 7.
Why gaps are left between rails on a railway track ?
Answer:
The length of the rails increases in summer due to high temperature. Therefore a gap is left to allow this expansion.

Question 8.
Find the increase in the temperature of aluminium rod if its length is to be increased by 1% (α for aluminium = 25 × 10^-6/ °C).
Answer:
Percentage increase in length = \(\frac{l_2-l_1}{l_1}\) × 100
α(t₂ – t₁) × 100 [∴ \(\frac{l_2-l_1}{4}\) = α(t₂ – t₁)]
Here, Percentage increase in length = 1
α = 25 × 10^-6/ °C
1 = 25 × 10^-6(t₂ – t₁) × 100
t₂ – t₁ = \(\frac{1}{25 \times 10^{-4}}\) = \(\frac{10^4}{25}\) = 400°C

Question 9.
Define mean free path.
Answer:
The average distance covered by a molecule between two successive collisions is called the mean free path.

Question 10
When does a real gas behaves like an ideal gas ?
Answer:
At low pressures and high temperatures real gases behave like an ideal gas.

Section – B (6 × 4 = 24)

Note :

• Answer any SIX questions.
• Each Question carries FOUR marks.
• ALL are short answer type questions.

Question 11.
A car travels the first third of a distance with a speed of 10 kmph, the second third at 20 kmph and the last third at 60 kmph. What is its mean speed over the entire distance ?
Answer:
V₁ = 10 kmph, V₂ = 20 kmph, V₃ = 60 kmph
<V> = \(\frac{3 V_1 V_2 V_3}{V_1 V_2+V_2 V_3+V_3 V_1}\)
= \(\frac{3 \times 10 \times 20 \times 60}{200+1200+600}\)
= \(\frac{36000}{2000}\)
<V> = 18 kmph

Question 12.
State Parallelogram law of vectors. Derive an expression for the magnitude and direction of the resultant vector.
Answer:
Statement: If two vectors acting at a point are represented by the adjacent sides of a parallelogram in magnitude and direction, then their resultant is represented by the diagonal of the parallelogram in magnitude and direction drawn from the same point.

Explanation : Let two forces \(\overrightarrow{\mathrm{P}}\) and \(\overrightarrow{\mathrm{Q}}\) act at a point O. Let θ be the angle between two forces. Let the side OA = \(\overrightarrow{\mathrm{P}}\) and OB = \(\overrightarrow{\mathrm{Q}}\). The parallelogram OACB is compelted. The points O and C are joined. Now OC = \(\overrightarrow{\mathrm{R}}\)

Resultant magnitude :
in fig \(\overrightarrow{\mathrm{OA}}\) = \(\overrightarrow{\mathrm{P}}\), \(\overrightarrow{\mathrm{OB}}\) = \(\overrightarrow{\mathrm{Q}}\). \(\overrightarrow{\mathrm{OC}}\) = \(\overrightarrow{\mathrm{R}}\)
in the triangle COD, OC² = OD² + CD²
OC² = (OA + AD)² + CD² (∵ OD = OA + AD)
OC² = OA² + AD² + 2OA. AD + CD62²
OC² = OA² + AC² + 2OA. AD
From Δ^le CAD, AD² + CD² = AC²

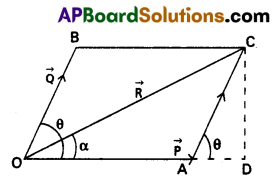
From Δ^leCAD, cos θ = \(\frac{A D}{A C}\) ………… (1)
AD = AC cos θ ………. (2)
∴ R² = p² + Q² + 2PQ cos θ
R= \(\sqrt{P^2+Q^2+2 P Q \cos \theta}\) …………… (3)

Resultant direction :
Let a be the angle made by the resultant vector with \(\overrightarrow{\mathrm{R}}\) with \(\overrightarrow{\mathrm{P}}\)
Then tan α = \(\frac{C D}{O D}\)
tan α = \(\frac{C D}{O A+A D}\) ………… (4)
In the triangle CAD, sin θ = \(\frac{C D}{A C}\)
CD = AC sin θ
CD = Q sin θ ………. (5)
tan α = (\(\frac{\mathrm{Q} \sin \theta}{\mathrm{P}+\mathrm{Q} \cos \theta}\)) (∵ AD – Q cos θ) ………… (6)
a = tan^-1\(\frac{\mathrm{Q} \sin \theta}{\mathrm{P}+\mathrm{Q} \cos \theta}\)

Question 13.
Mention the methods used to decrease friction.
Answer:

• Polishing : By polishing the surfaces of contact, friction can be reduced.
• Bearings : The rolling friction is less than the sliding friction hence free wheels of a cycle, motor car, dynamos etc., are provided with ball bearings to reduce friction. Bearings convert sliding motion into rolling motion.
• Lubricants : The lubricant forms a thin layer between surfaces of contact. It reduces the friction. In light vehicles or machines, oils like “three in one” are used as lubricants. In heavy machines grease is used. In addition to this they guard the mechanical parts from over heating.
• Streamlining : Automobiles and Aeroplanes are stream-lined to reduce the friction due to air.

Question 14.
Distinguish between centre of mass and centre of gravity.
Answer:

Centre of mass	Centre of gravity
1. Point at which entire mass of the body is supposed to be concentrated, and the motion of the point represents motion of the body.	1. Fixed point through which the weight of the body act.
2. It refers mass of to body.	2. It refers to the weight acting on all particles of the body
3. In a uniform gravitational field centre of mass and centre of gravity coincide	3. In a non-uniform gravitational field, centre of gravity and centre of mass do not coincide.
4. Centre of mass of the body is defined to describe the nature of motion of a body as a whole.	4. Centre of gravity of body is defined to know the amount of stability of the body when supported.

Question 15.
Define vector product. Explain the properties of a vector product with two examples.
Answer:
The cross product of two vectors is given by \(\vec{C}\) = \(\vec{A}\) × \(\vec{B}\) . The magnitude of the vector defined from cross product of two vectors is equal to product of magnitudes of the vectors and sine of angle between the vectors.

Direction of the vectors is given by right hand corkscrew rule and is perpendicular to the plane containing the vectors.
∴ | \(\vec{C}\) | = AB sin θ. and \(\vec{C}\) = AB sin θ n̂.
When, n̂ is the unit vector perpendicular to the plane containing the vectors \(\vec{A}\) and \(\vec{B}\)

Example :
1) Torque is cross product of position vector and Force.
i.e., \(\vec{T}\) = \(\vec{r}\) × \(\vec{F}\)

2) Angular momentum is cross product of position vector and momentum
i.e., \(\vec{L}\) = \(\vec{r}\) × \(\vec{P}\)

Properties :
1) Cross product does not obey commutative law. But its magnitude obey’s commutative law.
\(\vec{A}\) × \(\vec{B}\) ≠ \(\vec{B}\) × \(\vec{A}\) = (\(\vec{A}\) × \(\vec{B}\)) = – (\(\vec{B}\) × \(\vec{A}\)) , |(\(\vec{A}\) × \(\vec{B}\))| = |(\(\vec{B}\) × \(\vec{A}\))|

2) It obeys distributive law \(\vec{A}\) × (\(\vec{B}\) × \(\vec{C}\)) = \(\vec{A}\) × \(\vec{B}\) + \(\vec{A}\) × \(\vec{C}\)

3) The magnitude of cross product of two vectors which are parallel is zero.
Since θ = 0; | \(\vec{A}\) × \(\vec{B}\) | = AB sin 0° = 0

4) For perpendicular vectors, θ = 90°, | \(\vec{A}\) × \(\vec{B}\) | = AB sin 90° | n̂ | = AB

Question 16.
What is a geostationary satellite ? State its uses.
Answer:
Geo – Stationary satellite : If the period of revolution of an artificial satellite is equal to the period of rotation of earth, then such a satellite is called geostationary satellite.
Tjme period of geo – stationary satellite is 24 hours.

Uses :

1. Study the upper layers of atmosphere.
2. Fore most the changes in atmosphere.
3. Know the shape and size of the earth.
4. Identify the minerals and natural resources present inside and on the surface of the earth.
5. Transmit the T.V. programmes to distant objects
6. Under, take space research i.e., to know about the planets, satellites, comets etc.

Question 17.
Define strain and explain the types of strain.
Answer:
Stress : The restoring force per unit area is called stress
∴ Stress = \(\frac{\text { Restoring Force }}{\text { Area }}\) = \(\frac{F}{A}\)

Stress is classified into three types :
1) Longitudinal stress
2) Volume (or) Bulk stress
3) Tangential (or) shearing stress

1. Longitudinal stress (or) Linear stress : When a normal stress changes the length of a body, then it is called longitudinal stress.
Longitudinal stress = \(\frac{F}{A}\).

2. Volume (or) Bulk stress : When a normal stress changes the volume of a body, then it is called volume stress.
Volume stress = \(\frac{\text { Force }}{\text { Area }}\) = pressure.

3. Tangential (or) shearing stress : When the stress is tangential to the surface due to the application of forces parallel to the surface, then the stress is called tangential stress.
Tangential stress = \(\frac{F}{A}\) .

Question 18.
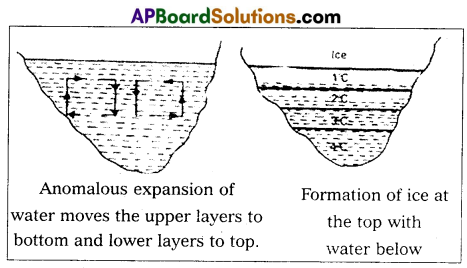
In what way is the anomalous behaviour of water advantageous to aquatic animals ?
Answer:
In cold countries, as atmospheric temperature decreases, the upper layer of the lakes, rivers etc., cool, contract and sink to the bottom (fig). This goes on until the whole of the water reaches the temperature of 4°C. When the top layers cool further temperature falls below 4°C, it expands and becomes lighter. It does not sink downwards and remains at the top. With further cooling the top layer gradually form ice at the top (fig). Ice and water are bad conductors of heat. So the lower layers are protected against freezing by the layers of ice and cold water at 1°C, 2°C and 3°C. This results in water remaining at the bottom at 4°C. So that aquatic animals survive in those layers of water.

Section – C (2 × 8 = 16)

Note :

• Answer any TWO questions.
• Each Question carries EIGHT marks.
• ALL are short answer type questions.

Question 19.
What are collisions ? Explain the possible types of collisions. Develop the theory of one dimensional elastic collision.
Answer:
Collisions : A strong interactions between bodies that occurs for a very short interval during which redistribution of momenta occur ignoring the effect of other forces are called collisions.

Collisions are of two types :

1. Elastic collision : The collision in which both momentum and kinetic energy is constant is called elastic collision.
2. Inelastic collision : The collision in which momentum remains constant but not kinetic energy is called Inelastic collision.

Elastic collision in one dimension : Consider two spheres (bodies) which have smooth, non-rotating of masses m₁ and m₂(m₁ > m₂) are moving along the straight line joining their centres of mass with initial velocities u₁ and u₂ (u₁ > u₂).’They undergo head on collision and move along the same line after collision with final velocities v₁ and v₁. These two bodies exert forces on each other during collision.

Hence both momentum and kinetic energy are conserved. According to law of conservation of linear momentum.

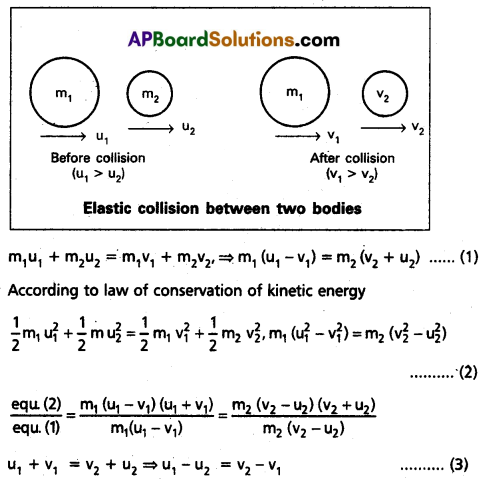
From the above equation, in one dimensional elastic collision, the relative velocity of approach before collision is equal to the relative velocity of separation after collision.
From equation (3) u₁ – u₂ = – v₁ + v₂, v₂ = u₁ – u₂ + v₁ …….. (4)
Sub equation (4) in equation (1) we get

Question 20.
Show that the motion of a simple pendulum is simple harmonic and hence derive an equation for its time period. What is seconds pendulum ?
Answer:

Let ‘S’ be the point of suspension of a simple pendulum. Let ‘l’ be its length, which is equal to the distance between the point of suspension and the centre of mass of the bob. Let ‘A’ be its mean position.

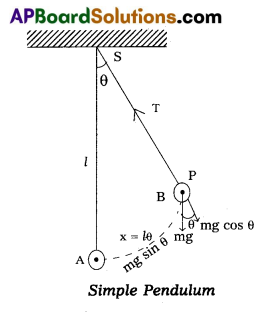
Let the simple pendulum be displaced through a small angle and released. Let the bob be in the position B at some instant.
AB = x = displacement from the mean position.
At B the forces acting on the bob are,
1) Weight ‘mg’ of the bob acting vertically downwards.
2) Tension ‘T’ in the string.

Weight can be resolved into two components, they are mg cosθ, mg sinθ.
mg cos θ balances the tension ‘T’ in the string.
The unbalanced component of mg is mg sin θ. This accelerates the bob towards the centre that is why it is known as restoring force.
∴ Restoring force F = – mg sin θ
∴ Acceleration a = \(\frac{\text { Force }}{\text { mass }}\) = \(\frac{-m g \sin \theta}{m}\)
= – g sin θ
If θ is small, then sin θ ≅ θ
∴ a = – gθ
But angle θ = \(\frac{\text { arc }}{\text { radius }}\) = \(\frac{x}{l}\)
a = -g \(\frac{x}{l}\)
a = -(\(\frac{g}{l}\))x → (1)
Since ‘g’ and ‘l’ are constants as, a ∝ – x
So the acceleration ∝ – displacement and it is directed towards mean position “O”. Hence it executes SHM.
The general equation for S.H.M. is
a = – ω²y → (2)
Comparing (1) and (2)
ω² = \(\frac{g}{l}\)
ω = \(\sqrt{\frac{g}{l}}\)
\(\frac{2 \pi}{T}\) = \(\sqrt{\frac{g}{l}}\)
T = \(\frac{2 \pi}{\sqrt{\frac{g}{l}}}\)
⇒ T = 2π\(\sqrt{\frac{l}{g}}\)
Where T is the time period of the simple pendulum.

Seconds pendulum : A pendulum whose time period is equal to 2 seconds is called seconds pendulum. It is used in pendulum clocks.
Its length changes with acceleration due to gravity.

Problem :
T = 2π\(\sqrt{\frac{l}{g}}\)
T = 2 sec, g = 9.8 m/s²
2 = 2π\(\sqrt{\frac{l}{g}}\)
l = \(\frac{\mathrm{g}}{\pi^2}\) = \(\frac{9.8}{(3.14)^2}\) = lm (or) 10 cm.

Question 21.
Explain reversible and irreversible processes. Describe the working of Carnot engine obtain an expression for the efficiency.
Answer:
Reversible process : A process that can be retraced back in the opposite direction in such away that the system passes through the same states as in the direct process, and finally the system and the surroundings return in their original states, is called a reversible process.
A reversible process is only a purely idealised process.

Examples :

1. Slow isothermal and slow adiabatic changes.
2. Peltier effect and seeback effect.
3. Fusion of ice and vaporisation of water.

Irreversible process : “A process that cannot be retraced back in the opposite direction” is called as irreversible process.
In this process the system does not pass through the same intermediate states as in the revesible process.
All natural processes such as conduction, radiation, radioactivity etc., the irreversible.

Example :

1. Work done against friction.
2. Heat produced in conductors by passing a current through it. (Joule heating)
3. Diffusion of gases.

Carnot Engine : A reversible heat engine operating between two temperatures is called a carnot engine. The cycle operating it is known as carnot’s cycle. In this cycle the working substance (say an ideal gas) is taken through a cycle by means of two isothermals and two adiabatics. The four operations are shown in P – V (indicator) diagram.

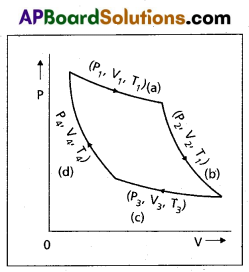
Step 1 → 2 : Isothermal expansion of the gas taking its state from (P₁, V₁, T₁) to (P₂, V₂, T₂). It is shown in curve (a).
The heat absorbed by the gas (Q₁) from the reservoir at temperature T₁ equals the workdone by the gas. i.e.
W_{1 → 2} = Q₁ = μRT₁
log_e \(\frac{V_2}{V_1}\) → (1)

Step 2 → 3 : Adiabatic expansion of the gas from (P₂, V₂, T₁) to (P₃, V₃, T₂). It is shown in curve (b). The work done by the gas is given by
W_{2 → 3} = \(\frac{\mu R\left(T_1-T_2\right)}{(r-1)}\) → (2)

Step 3 → 4 : Isothermal compression of the gas from (P₃, V₃, T₂) to (P₄, V₄, T₂). It is shown in curve (c).
Heat released (Q₂) by the gas to the reservoir at temperature T₂ equals the work done on the goes.
i.e., W_{3 → 4} = μRT₂ log_e\(\frac{V_4}{V_3}\) = – μ RT₂ log_e\(\frac{V_3}{V_4}\)

Step _{4 → 1} : Adiabatic compression of the gas from (P₄, V₄, T₂) to (P₁, V₁, T₁). It is shown incurve (d).
W_{4 → 1} = μR \(\frac{\left(T_2-T_1\right)}{(r-1)}\) = – μR \(\frac{\left(T_1-T_2\right)}{(r-1)}\)
Total workdone by the gas in one complete cycle is
W = W_{1 → 2} + W_{2 → 3} + W_{3 → 4} + W_{4 → 1}