AP Inter 1st Year Physics Important Questions Chapter 12 Thermal Properties of Matter

Students get through AP Inter 1st Year Physics Important Questions 12th Lesson Thermal Properties of Matter which are most likely to be asked in the exam.

AP Inter 1st Year Physics Important Questions 12th Lesson Thermal Properties of Matter

Very Short Answer Questions

Question 1.
Distinguish between heat and temperature.
Answer:

HEAT	TEMPERATURE
1) Fleat is a form of energy.	1) Temperature is a measure of thermal energy.
2) C.G.S unit: Calorie S.I unit: joule	2) C.G.S unit: °C S.I unit: kelvin
3) A calorimeter is used to measure the amount of heat in a substance	3) A thermometer is used to measure the temperature of a substance.

Question 2.
What are the Sower and upper fixing points in Celsius and Fahrenheit scales? [AP 19]
Answer:
On Celsius scale of temperature, the lower fixed point is 0°C and the upper fixed point is 100HC. On Fahrenheit scale of temperature, the lower fixed point is 32°F and the upper fixed point is 212°F.

Question 3.
Do the values of coefficients of expansion differ when the temperatures are measured on Centigrade scale or on Fahrenheit scale? [Imp.Q]
Answer:
Yes. One degree interval on Fahrenheit scale is less than one degree interval on Celsius scale. Since, x(°C)^-1 = x × \(\frac{5}{9}\)(°F)^-1

Question 4.
Can a substance contract on heating? Ciive an example. [TS 16,18][AP 18, 22]
Answer:
Yes.
Ex: Cast iron, Natural Rubber( an alloy of lead, tin & antimony), type metal and pure water between 0°C to 4°C.

Question 5.
Why gaps are left between rails on a railway track?
Answer:
A small gap is left between the ends of successive rails on a railway track.
This is to allow linear expansion of rails in summer.

Question 6.
Why do liquids have no linear and areal expansions? [TS 19][Imp.Q]
Answer:
Liquids have no shape of their own. They always take the shape of the vessel. Flence they do not have coefficients of Linear and Areal expansion.

Question 7.
What is latent heat of fusion?
Answer:
Latent heat of fusion of ice :
The latent heat of fusion of ice is the amount of heat required to convert ‘unit mass of water’ at 0°C into ice at 0°C.
For water, the latent heat of fusion is 80 calgm^-1 (or) 3.33 × 10⁵ Jkg^-1

Question 8.
What is latent heat of vapourisation? [Imp.Q]
Answer:
Latent heat of vapourisation of water :
The amount of heat required to change ‘unit mass of a liquid’ into vapour, at constant temperature is called Latent heat of Vapourisation.

For water the latent heat of vapourisation 540 calgm^-1 (or) 2.26 × 10⁶ J/kg.

Question 9.
What is specific gas constant? Is it same for all gases?
Answer:
The universal gas constant per unit mass is called ‘specific gas constant’, i.e r = \(\frac{R}{M}\)

No. It is not same for all gases. It is different for different gases.

Question 10.
What are the units and dimensions of specific gas constant? [Imp.Q]
Answer:
S.I Unit: J Kg^-1 K^-1 ;
Dimensional formula: [ M° L² T^-2 K^-1]

Question 11.
Why utensils are coated black? Why the bottom of the utensils are made of copper? [AP, TS 18]
Answer:
Since black bodies are good absorbers of heat, utensils are coated black to absorb heat energy falling on them. Copper is a good conductor of heat. Hence it promotes the distribution of heat over the bottom of a vessel for uniform cooking.

Question 12.
State Weins displacement law? [TS 20][AP 17, 19]
Answer:
Weins displacement law :
The wavelength(λ_m) for which energy is maximum is inversely proportional to absolute temperature of the body.

Wein’s constant is 2.9 × 10^-3 mK

Question 13.
Ventilators are provided in rooms just below the roof. Why?
Answer:
Hot air has less density. So it moves upwards due to convection.

To escape this hot air outoff the room, ventilators are provided just below the roof.

Question 14.
Does the body radiate heat at OK? Does it radiate heat at 00C? [Imp.Q]
Answer:

1. No, the body does not radiate heat at OK.
2. Yes, the body radiates heat at 0°C.

Question 15.
State the different modes of transmission of heat. Which of these modes require medium? [TS 18][Imp.Q]
Answer:
There are three distinct modes of heat transfer :

1. Conduction
2. Convection and
3. Radiation

Conduction and convection of heat are required material medium.

Question 16.
Define coefficient of thermal conductivity and temperature gradient. [Imp.Q]
Answer:
The quantity of heat flowing normally per second through unit area of the substance per unit temperature gradient is called “coefficient of thermal conductivity”.

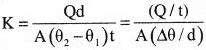
The change in temperature per unit distance moved in the direction of flow of heat is called temperature gradient. Temperature gradient = \(\frac{\left(\theta_2-\theta_1\right)}{\mathrm{d}}=\frac{\Delta \theta}{\mathrm{d}}\)

Question 17.
What is thermal resistance of a conductor? On what factors does it depend? [Imp.Q]
Answer:
The resistance offered by the conductor for the flow of heat through it is called “Thermal resistance”.

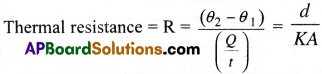
Thermal resistance depends on
i) the nature of the material (i.e thermal conductivity K)
ii) the geometry of the object (d/A).

Question 18.
State the units and dimensions of coefficient of convection. [Imp.Q]
Answer:

Question 19.
Define emissive power and emissivity. [Imp.Q]
Answer:
Emissive Power :
The energy radiated by a body per second per unit area of the body, at a given temperature and wave length, is called emissive power of the body.

Emissivity :
The ratio of the emissive power of a body to that of black body, at the same temperature is called Emissivity.

Question 20.
What is greenhouse effect? Explain global warming. [Imp.Q][TS 19; AP 15]
Answer:
Greenhouse effect :
The thermal radiation from earth’s surface absorbed by atmospheric greenhouse gases(carbon dioxide, methane, nitrous oxide) is re-radiated in all directions.

A part of this re-radiation reflects back towards the surface of the earth. It results in heating up of earth’s surface and atmosphere.

Global warming :
Global warming is the ‘observed and projected increase’ in the average temperature of Earth’s atmosphere and oceans. The Earth’s average temperature has increased by 0.3°C to 0.6°C since the beginning of this century’.

Question 21.
Define absorptive power of a body. What is the absorptive power of a perfect blackbody.
Answer:
Absorptive power :
The ratio between energy flux absorbed in certain time to total energy flux incident on the body in the same time is known as absorptive power.

The absorptive power of a black body is 1.

Question 22.
State Newton’s law of cooling. [TS 18, 19][AP 15, 16, 18, 20]
Answer:
Newton’s law of cooling states that the ‘rate of loss of heat of a hot body’ is directly proportional to the ‘difference in temperature’ between the ‘body and its surroundings’.

Question 23.
State the conditions under which Newton’s law of cooling is applicable. [TS 15]
Answer:
Newton’s law of cooling is applicable when

1. Heat lost by the body is mainly due to convection
2. Loss of heat is negligible by conduction
3. The hot body is cooled by forced convection
4. The temperature of every part of the body is same

Question 24.
The roof of buildings are often painted white during summer. Why? [TS 15, 17][AP 16]
Answer:
White paint is a good reflector of heat. Good reflector is a bad absorber of heat.
So buildings that are painted white to keep cool during summer.

Short Answer Questions

Question 1.
Explain Celsius and Fahrenheit scales of temperature. Obtain the relation between Celsius and Fahrenheit scales of temperature. [TS 19, 22]
Answer:
Celsius scale :
This scale was invented by Celsius. It is used in scientific works. On this scale, the ice point is taken as 0°C and the steam point is taken as 100°C. This interval 100° is divided into 100 equal parts, each part corresponding to 1°C

Fahrenheit scale :
This was invented by Fahrenheit. lt is used in clinical works. On this scale, the ice point is taken as 32°F and the steam point is taken as 212°F. This interval 180° is divided into 180 equal parts, each part corresponding to 1°F.

Relation between Celsius and Fahrenheit scales:

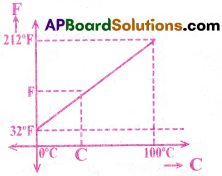
A relationship for converting temperature from one scale to the other may be obtained from a graph of Fahrenheit F
temperature versus Celsius temperature C is a straight line as shown in the figure, from graph

This equation is in the form of y = mx + c. So the graph is a straight line.

Question 2.
Two identical rectangular strips one of copper and the other of steel are riveted together to form a compound bar. What will happen on heating?
Answer:

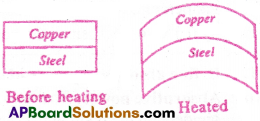
1. The coefficient of linear expansion of copper is greater than that of steel.
2. Therefore, when bimetallic strip made of copper and steel is heated, copper strip expands more than the Before heating steel strip.
3. Since the two are rivetted together, the bimetallic strip bends so as to allow more expansion in the copper strip.
4. As a result, the copper strip lies on convex side of the bent bimetallic strip.

Question 3.
Pendulum clocks generally go fast in winter and slow in summer. Why? [TS 17, 19][AP 19]
Answer:

1. The time period of pendulum clock is given by T = 2π\(\sqrt{\frac{l}{g}}\)
   At a given place, T ∝ √l (∵ g is constant)
2. The pendulum of a clock expands in summer, so its time period increases.
   Hence, it makes less number of oscillations than required per day. Hence it will lose time or clock goes slow.
3. The pendulum of a clock contracts in winter, its length decreases so its time period decreases. Hence, it makes more number of oscillations than required per day.
4. Hence it will gain time or clock goes fast.

Question 4.
In what way is the anomalous behaviour of water advantageous to aquatic animals? [TS 18; AP 17, 18, 22]
Answer:

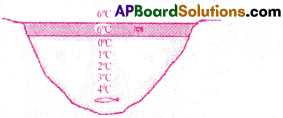
1. When temperature increases from 0°C to 4°C water contracts instead of expansion. Hence water attains maximum density at 4°C. This is called anomalous behaviour of water.
2. During winter, when the temperature of the atmosphere falls below 0°C, the surface of lakes and rivers gradually freezes to ice.
3. But ice is bad conductor of heat. Under the frozen upper layers, the water remains in its liquid form and does not freeze.
4. Thus aquatic animals like fish are survived in this water.

Question 5.
Explain conduction, convection and radiation with examples. [AP 19, 20; AP, TS 15, 16, 20]
Answer:
Conduction :
The heat transfer from one place to another place without the actual movement of the particles is called conduction. [TS 18]
Ex: Heat transfer takes place from the hot end of the rod to the other end by conduction.

Convection :
The Heat transfer from one place to another place with the actual movement of particles is called convection. It is possible in only in fluids. Convection can be natural or forced. Ex: Sea breeze, Land breeze, Trade wind

Radiation :
Heat transfers from one place to another place without the help of the material of the medium is called Radiation. It arises due to electro magnetic radiation emitted by a body by virtue of tis temperature. Radiation is the quickest mode of heat transmission.
Ex: Transfer of heat energy from the Sun.

Question 6.
Write short notes on Triple point of water? [TS 15; AP 16]
Answer:

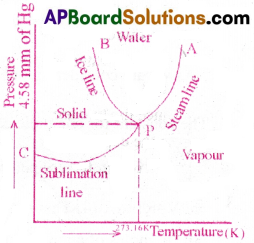
The point at which the three phases of matter co-exist in equilibrium is called Triple point.

Its coordinates for water are P (273.16K, 4.58 mm of Hg) A graph is drawn between temperature and pressure of a substance. It describes distinct phases of physical states at equilibrium and is called Phase diagram.

Ice Line(PB) :
The temperature at which the solid and liquid states are in equilibrium is called the Melting point. It is along the curve PB and is called ice line.

Steam Line (PA) :
The temperature at which liquid and vapour states are in equilibrium is called Steam point. It is along the curve PA and is called steam line.

Sublimation line :
The temperature at which solid and vapour states are in equilibrium is called Sublimation point. It is along the curve PC and is called sublimation line.

The 3 curves PB, PA and PC meet at a single point ‘P’, called the Triple point of water.

Long Answer Questions

1. State Boyle’s Saw and Charle’s law. Hence derive ideal gas equation. Which of the two laws is better for the purpose of thermometry and why? [AP, TS 15]
Answer:
Boyle’s law :
At a given temperature, the pressure of a given mass of a gas is inversely proportional to its volume. [AP 18]

Charles law :
At constant pressure, the volume of a given mass of a gas is directly proportional to its temperature (in Kelvin scale). [AP 18]

Ideal gas equation :
Consider one mole of an ideal gas initially at a pressure P0, volume V0 and temperature T0 (in Kelvin scale).

i) Keeping the pressure PQ constant, let the temperature of the gas be changed to T.

By Charles law, at constant pressure P0, the volume V0 at temperature T0 is changed to new volume V1 at temperature T. Then the relation between these quantities is as follows:

The constant for one mole of the gas is denoted by R and is called Universal gas constant.
\(\frac{P_0V_0}{T_0}\) = R for one mole then equation (3) becomes \(\frac{PV}{T}\) = R

⇒ PV = RT …….. (4) This is the ideal gas equation for one mole of an ideal gas.
For ‘n’ moles of a gas, the ideal gas equation is given by PV = nRT ……… (5)

Charles law is better for the purpose of thermometry:
Because in case of Boyle’s law, temperature is kept constant. So it is not useful for thermometry. But incase of Charles law, by keeping volume constant, we can measure different temperatures at different pressures. Similarly, by keeping pressure constant, we can measure different temperatures at different volumes. So we can use Charles law for the purpose of thermometry.

Question 2.
Explain thermal conductivity and coefficient of thermal conductivity.
A copper bar of thermal conductivity 401 W/(mK) has one end at 104°C and the other end at 24°C. The length of the bar is 0.10 m and the cross-sectional area is 10 x 10^-6m². What is the rate of heat conduction along the bar?
Answer:
Thermal conductivity :
The ability to conduct heat in solids by conduction is called thermal conductivity.

Coefficient of thermal conductivity :
Consider a rectangular slab of area ‘A’. Its two faces ‘E’ and ‘F’ are maintained at temperatures θ₂°C and θ₁°C respectively [θ₂°C > θ₁°C ]. Let ‘Q’ be the amount of heat transmitted by conduction at steady state conditions between the faces ‘E’ and ‘F’ separated by a distance ‘d’ as shown in figure.

The amount of heat transmitted between these two faces by thermal conduction is directly proportional to
(i) the area of the cross-section of the slab ‘A’.
(ii) the temperature difference between the faces (θ₂ – θ₁)°C
(iii) the time of flow of heat(t)
(iv) inversely proportional to the distance between the two faces (d) i.e.,

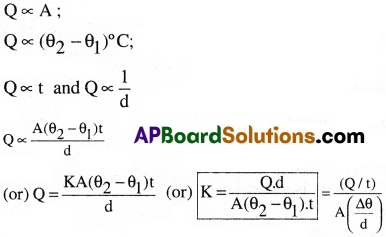
Where ‘K’ is known as the coefficient of thermal conductivity.

Definition :
The coefficient of thermal conductivity of a material is defined as the quantity of heat flowing normally per second through unit area of the substance per unit temperature gradient.

Question 3.
State and explain Newton’s law of cooling. State the conditions under which Newton’s law of cooling is applicable. [TS 16, 22]
A body cools down from 60°C to 50″C in 5 minutes and to 40″C in another 8 minutes. Find the temperature of the surroundings. [May 13]
Answer:
Newton’s law of cooling :
Newton’s law of cooling states that the rate of loss of heat of a hot body is proportional to the difference in temperatures between the body and its surroundings. Here, the difference in temperatures should be small and the nature of the radiating surface should remain same.

If the average temperature of the body is T, temp, of its surrounding is T_S and rate of loss of

Conditions for Newton’s law of cooling:

1. Heat lost by the body is mainly due to convection
2. Loss of heat is negligible by conduction
3. The hot body is cooled by forced convection
4. The temperature of every part of the body is same
5. Temperature differences are moderate.

Problem:

Exercise Problems

Question 1.
What is the temperature for which the readings on Kelvin and Fahrenheit scales are [May 2010]
Solution:

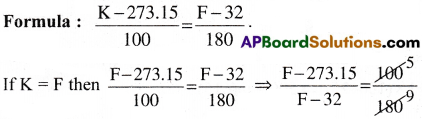
⇒ 9(F – 273.15) = 5(F – 32) ⇒ 9F – 9(273.15) = 5F – 5(32)
⇒ 4F = 9(273.15) – 5(32) ⇒ F = 574.6
∴ 574.6 K = 574.6° F

Question 2.
Find the increase in temperature of aluminium rod if its length is to be increased by 1%. (a for aluminium = 25 × 10^-6/°C). [AP 15, 22]
Solution:
Given that a = 25 × 10^-6/°C

Question 3.
The mass of a litre of gas is 1.562g at 0″C under a pressure of 76 cm of mercury. The temperature is increased to 250″C and the pressure to 78cm of mercury. What is the mass of one litre of the gas under new conditions?
Solution:
Given that m₁ = 1.562g, V₁ = 1 L, P₁ = 76cm of Hg.
T₁ = 0°C = 273°K, P₂ = 78cm of Hg, V₂ = 1 L, T₂ = 250°C = 250 + 273 = 523 K

Question 4.
The volume of a mass of gas at 37°C and a pressure of 75cm of mercury is 620cc. Find the volume at N.T.P.
Solution:
Given that P₁ = 75cm ofHg. V₁ = 620cc, T₁ = 273 + 37 = 310°K At
At NTP, P₂ = 76cm of Hg, T₂ = 273K

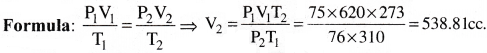
Question 5.
How much steam at 100°C is to be passed into water of mass 100g at 20°C to raise its temperature by 5°C? (Latent heat of steam is 540 cal/g and specific heat of water is 1 cal/g°C).
Solution:
Given that t₂ =100°C, m₁ = 100g, t₁ = 20°C, t₃ = t₁ + 5 = 20 + 5 = 25°C
L = 540 cal/gm, S = 1 cal/g°C.
Heat gained by cold body = Heat lost by hot body
If m is the mass of vapour to be added, then m₁s (t₃ – t₁) = mL + ms (t₂ – t₃)
⇒ 100 × 1 × (25 – 20) = m(540 + 1 × (100 – 25)) ⇒ 500 = m(615)
⇒ m = \(\frac{500}{615}\) = 0.813gm

Question 6.
2kg of air is heated at constant volume. The temperature of air is increased from 293K to 313K. If the specific heat of air at constant volume is 0.718 k.J/kg K, find the amount of heat absorbed in kJ and keal. (J = 4.2 k.)/kcnl)
Solution:
Given tha, m = 2kg, T₁ = 273 K, T₂ = 313 K
Also, C_v = 0.718 kJ/Kg K, J = 4.2 kJ /k cal
∴ Q = mC_v(T₂ – T₁) = 2 × 0.718 × (313 – 273) = 28.72 kJ = \(\frac{28.72}{4.2}\) = 6.838 k cal.

Question 7.
A clock with a brass pendulum keeps correct time at 200C but loses 8.212 sec per day, when the temperature rises to 300C. Calculate the coefficient of linear expan¬sion of brass.
Solution:
Time loss by the pendulum clock per a day = \(\frac{1}{2}\) α ∆t × 86400 sec
Given Time loss per a day = 8.212 sec, ∆t= (30 – 20) = 10°C
⇒ 8.212 = \(\frac{1}{2}\) α × 10 × 86400
∴ α = \(\frac{8.212\times2}{10\times86400}\) = 0.019 × 10^-3 = 19 × 10^-6/°C

Question 8.
If the volume of nitrogen of mass 14 kg is 0.4 m3 at 30°C, calculate the pressure.
Solution:
PV = nRT
Here V = 0.4 m³, T = 30 + 273 = 303K, R = 8.314 J/mole x K

Question 9.
A body cools from 60°C to 40″C in 7 minutes. What will be its temperature after next 7 minutes, if the temperature of its surrounding is 10°C?
Solution:

Question 10.
If the maximum intensity of radiation for a black body is found at 2.65 pm. Find the temperature of the radiating body. [TS 19]
Solution:
Given λ_m = 2.65 pm = 2.65 × 10^-6 m
From Wein’s displacement law λ_m T = b
Where b is Wein’s constant, b = 2.9 × 10^-3 mK,

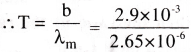
= 1.094 × 10³ K = 1094 K

Multiple Choice Questions

Question 1.
The temperature at which the reading of a Fahrenheit thermometer will be double that of a centigrade thermometer is
1) 160°C
2) 180°C
3) 32°C
4) 100°C
Answer:
4) 100°C

Question 2.
The variation of density of a solid with temperature is given by the formula

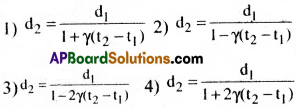
Answer:
1

Question 3.
Water has maximum density at
1) 4°C
2) 32°F
3) 0°C
4) 4°C
Answer:
1) 4°C

Question 4.
The apparent coefficient of expansion of a liquid, when heated in a copper vessel is ‘C’ and when heated in a silver vessel is ‘S’. If ‘A’ is the linear coefficient of expansion of copper, then the linear, coefficient of expansion of silver is

Answer:
2

Question 5.
The pressure of a given mass of gas is 100cm at 127°C. The pressure of the same mass of gas having the same volume at 27°C is
1) 75 cm
2) 76 cm
3) 84 cm
4) 64 cm
Answer:
1) 75 cm

Question 6.
A perfect gas at 27°C is heated at constant pressure so as to double its volume. The temperature of the gas will be
1) 273°C
2) 327°C
3) 237°C
4) 360°C
Answer:
1) 273°C

Question 7.
One mole of gas occupies 100ml at 50 mm pressure. The volume of 2 moles of the gas at 100 mm pressure and same temperature is
1) 50 ml
2) 100 ml
3) 200 ml
4) 500 ml
Answer:
2) 100 ml

Question 8.
The pressure of a gas in a closed vessel is increased by 0.4%, if the temperature of the gas is increased by 1°C, the initial temperature of the gas is
1) 23°C
2) 250°C
3) -23°C
4) 300K
Answer:
3) -23°C

Question 9.
The temperature of the sun is about 6000K and maximum intensity is emitted at 4800A° from it. If the sun cools to 3000K, then the peak intensity would occur at
1) 4800A°
2) 9600A°
3) 2400A°
4) 19200A°
Answer:
1) 4800A°

Question 10.
If the temperature of the sun were to increase from T to 2T and its radius from R to 2R, then the ratio of the radiant energy received on earth to what it was previously will be
1) 4
2) 16
3) 32
4) 64
Answer:
4) 64

Question 11.
If λ_m denotes the wavelength at which the radiative emission from a black body at a temperature T K is maximum, then
1) λ_m = T⁴
2) λ_m is independent of T
3) λ_m ∝ T
4) λ_m ∝ T^-1
Answer:
4) λ_m ∝ T^-1

Question 12.
A black body has maximum wavelength λ_m at 2000 K. Its corresponding wavelength at 3000 K will be

Answer:
2

Question 13.
A black body at 1227°C emits radiations with maximum intensity at a wavelength of 5000 A°. If the temperature of the body is increased by 1000°C, the maximum intensity will be observed at
1) 3000 A°
2) 4000 A°
3) 5000 A°
4) 6000 A°
Answer:
1) 3000 A°

Question 14.
Mercury thermometer can be used to measure temperature upto
1) 260°C
2) 100°C
3) 360°C
4) 500°C
Answer:
3) 360°C

Question 15.
The value of coefficient of volume expansion of glycerin is 5 × 10^-4 K^-1. The fractional change in the density of glycerin for a rise of 40°C in its temperature, is
1) 0.025
2) 0.010
3) 0.015
4) 0.020
Answer:
4) 0.020

Question 16.
The density of water at 20°C is 998 kg/m³ and at 40°C is 992 kg/m³. The coefficient of volume expansion of water is
1) 3 × 10^-4/°C
2) 2 × 10^-4/°C
3) 6 × 10^-4/°C
4) 10^-4/°C
Answer:
1) 3 × 10^-4/°C

Question 17.
Thermal capacity of 40 g of aluminium (s = 0.2 cal/g K) is
1) 168 J/K
2) 672 J/K
3) 840 J/K
4) 33.6 J/K
Answer:
4) 33.6 J/K

Question 18.
If 1 g of steam is mixed with 1 g of ice, then resultant temperature of the mixture is
1) 100°C
2) 230°C
3) 270°C
4) 50°C
Answer:
1) 100°C

Question 19.
Equal masses of liquids A, B and C have temperatures 10°C, 25°C and 40°C respectively. If A and B are mixed, the mixtures has a temperature of 15°C. If B and C are mixed, the mixture has a temperature of 30°C. If A and C are mixed then the temperature of mixture is
1) 10°C
2) 35°C
3) 20°C
4) 25°C
Answer:
1) 10°C

Question 20.
Which of the following rods, (given radius r and length l) each made of the same material and whose ends are maintained at the same temperature will conduct most heat?
1) r = r₀, l = l₀
2) r = 2r₀, l = l₀
3) r = r₀, l = 2l₀
4) r = 2r₀, l = 2l₀
Answer:
4) r = 2r₀, l = 2l₀

Question 21.
The quantities of heat required to raise the temperature of two solid copper spheres of radii r( and r2 (r, = 1.5r2) through 1 K are in the ratio
1) 27/8
2) 9/4
3) 3/2
4) 5/3
Answer:
1) 27/8

Question 22.
A black body is at a temperature of 500K. It emits energy at a rate which is proportional to
1) (500)³
2) (500)⁴
3) 500
4) (500)²
Answer:
2) (500)⁴

Question 23.
If the temperature of the sun is doubled, the rate of energy received on earth will be increased by a factor of
1) 2
2) 4
3) 8
4) 16
Answer:
4) 16

Question 24.
A bimetallic strip is formed out of two identical strips one of copper and the other of brass. The coefficient of linear expansion of the two metals α_c and α_b. On heating, the temeprature of the strip increases by ∆t and strip bends in the form of axe of radius R. Then R is proprotional to

Answer:
2

Question 25.
A glass Hast if volume one litre is filled completely with mercury at 0°C, the flask is heated 100°C. Coefficient of volume expansion of mercury is 1.82 × 10^-4/°C and coefficient of linear expansion of glass is 0.1 × 10^-4/°C .During this process amount of mercury which over flask is
1) 450
2) 1000
3) 1800
4) 225
Answer:
3) 1800