AP Inter 1st Year Physics Important Questions Chapter 11 Mechanical Properties of Fluids

Students get through AP Inter 1st Year Physics Important Questions 11th Lesson Mechanical Properties of Fluids which are most likely to be asked in the exam.

AP Inter 1st Year Physics Important Questions 11th Lesson Mechanical Properties of Fluids

Very Short Answer Questions

Question 1.
Define average pressure. Mention it’s unit and dimensional formula. Is it a scalar or a vector?
Answer:
The average pressure is defined as the normal force acting per unit area.
P_avg = \(\frac{F}{A}\)
S.I unit: Nm^-2 (or) Pascal
Dimensional formula: [ML^-1T^-2]
It is a scalar quantity.

Question 2.
Define Viscosity. What are it’s units and dimensions? [May 13][AP, TS 15, 16, 18]
Answer:
Viscosity :
The property of a fluid which opposes the relative motion between different layers is called viscosity.
The S.I unit of viscosity is poiseiulle (pi) (or) pa s The dimensions of viscosity are [ML-1T-1]

Question 3.
What is the principle behind the carburetor of an automobile? [TS 17, 18; AP 15, 19, 19]
Answer:
The carburetor of an automobile works on Bernoulli’s principle.

Working :
The carburetor of automobile has a Venturi channel(nozzle) through which air flows with a large speed. The pressure is lowered at the narrow neck and the petrol is sucked up in the chamber to provide the correct mixture of air to fuel necessary for combustion.

Question 4.
What is magnus effect? [AP 15; TS 16, 19, 22]
Answer:
When a ball is moving forward with spinning then the velocity of air above the ball is larger and below it is smaller. Stream lines thus get crowded above and rarified below. This difference in the velocities of air results in the pressure difference between the lower and upper faces and there is a net upward force on the ball. This dynamic lift due to spinning is called Magnus effect.

Question 5.
Why arc drops and bubbles spherical? [IPE’ 13, 14, 14][AP, TS 16, 17, 18, 22]
Answer:
Due to surface tension rain drops and water bubbles are spherical in nature.

For a given volume, Sphere has minimum surface area. So liquid drops attain spherical shape.

Question 6.
Give the expression for the excess pressure in a liquid drop. [Imp.Q][TS 17, 20]
Answer:
Liquid drop in air has one interface.
Hence excess pressure in a liquid drop = P_inside – P_outside ⇒ P_excess = \(\frac{2T}{r}\)
Where r = radius of a liquid drop
T = surface tension of liquid-air interface.

Question 7.
Give the expression for the excess pressure in an air bubble inside the liquid. [Imp.Q]
Answer:
An air bubble inside the liquid has only one free surface.
The excess pressure is P_excess = \(\frac{2T}{r}\)

Question 8.
Give the expression for the excess pressure in the soap bubble in air. [AP 19; TS 16, 22]
Answer:
Soap bubble in air has two interfaces.
Hence excess pressure in soap bubble = P_inside – P_outside ⇒ P_excess = \(\frac{2T}{r}\)
Where r = radius of soap bubble;
T = surface tension of liquid-air interface.

Question 9.
What are water proofing agents and water wetting agents? What do they do? [AP 20]
Answer:
Water proofing agents are materials or fabrics that are impervious (not allowing fluid to pass through) to water. They increase the angle of contact between the water and fibres. Water Wetting agents are Soaps, detergents, and dying substances.
They increase penetrating and spreading ability.
They reduce the angle of contact as well as the surface tension of water.

Question 10.
Why water droplets wet the glass surface and does not wet lotus leaf? [TS 15]
Answer:
For glass surface angle of contact θ < 90°. So water drops wet the glass.
For lotus leaf angle of contact θ > 90°. So water drops does not wet the lotus leaf.

Question 11.
What is angle of contact? [TS 20][IPE, 14][AP 16]
Answer:
Angle of contact :
When a solid body is dipped in a Liquid,the angle between solid surface and the tangent drawn to the liquid surface, at the point of contact, inside the liquid, is called Angle of contact.
For Pure Water and glass, angle of contact is 0°.
For Mercury, angle of contact is 140°.

Question 12.
Mention any two examples that obey Bernoullis theorem and justify them. [Imp.Q][AP 18]
Answer:
Examples:
1) In heavy winds, house roofs are blown off, when the velocity of wind is greater on the rooftop than inside the house. Then the pressure on the rooftop becomes less than that inside the house. This pressure difference causes the dynamic lift and hence the roof is blown off.

2) When fan is rotating, papers are blown off the table top. The velocity of wind on the paper increases due to fan and hence pressure decreases.

Question 13.
When water flows through a pipe, which of the layers moves fastest and slowest?
Answer:
The water layer which is in contact with the walls of the pipe moves slower.
And the Central layer moves faster.

Question 14.
Terminal velocity is more if surface area of the body is more. True or false? Give reason. [Imp.Q]
Answer:
True.
Terminal velocity v_t ∝ r² ⇒ v_t ∝ 4πr² ⇒ V_t ∝ A, [Since, A = 4πr² = surface area of sphere]

Short Answer Questions

Question 1.
What is atmospheric pressure and how is it determined using Barometer? [Imp.Q]
Answer:
The pressure of atmosphere at any point is equal to the weight of air column of unit cross-sectional area extending from that point to the top of the atmosphere.

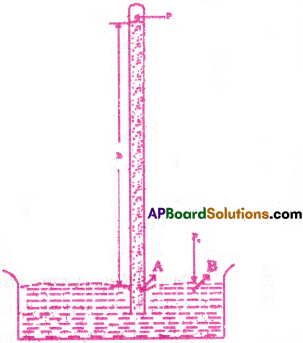
Barometer :
Mercury barometer consists of a long glass tube closed at one end and filled with mercury. It is inverted into a trough of mercury as shown in figure. The space above the mercury column in the tube contains only mercury vapour whose pressure(P) may be neglected. Points A and B are at same level.
Hence pressure at A = pressure at B
P_a = hρg
Where ρ = density of mercury
h = height of the mercury column in the tube
p_a = atmospheric pressure

Question 2.
What is gauge pressure and how is a manometer used for measuring pressure difference. [Imp.Q]
Answer:
The excess pressure (P – P_a) at a depth below the surface of a liquid open to the atmosphere is called a ‘gauge pressure’ at that point.

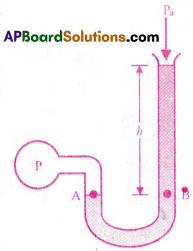
Manometer:
An open-tube manometer consists of a U-tube containing a suitable liquid. One end of the tube is open to the atmosphere and other end is connected to the system whose pressure we want to measure.
The pressure at A = pressure at B
P = P_a + hρg ⇒ P – P_a = hρg ∴ Gauge pressure = hρg
This gauge pressure is proportional to difference in heights(h) of mercury levels in manometer.

Question 3.
State Pascal’s law and verify it with the help of an experiment. [Imp.Q]
Answer:
Pascal’s law :
The pressure in a fluid at rest is the same at all points if they are at the same height.

Verification :
Consider an element ABCDEF in the form of a right-angled prism in the interior of a fluid at rest. This element is small so that the effect of gravity can be ignored. The areas of faces BEFC, ADFC and ADEB are A_a, A_b and A_c respectively. The fluid exerts pressures P_a, P_b and P_c on this element corresponding to the normal forces F_a, F_b and F_c as shown in figure.

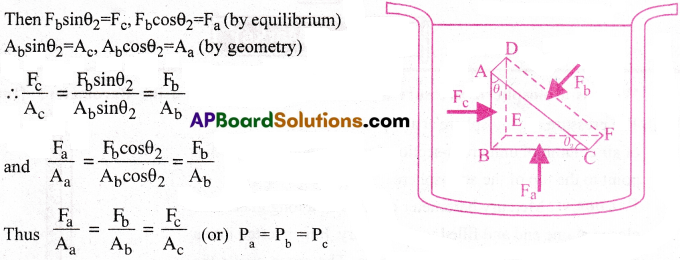
Hence pressure exerted is same in all directions in a fluid at rest.

Question 4.
Explain hydraulic lift and hydraulic brakes.
Answer:
Hydraulic lift :
In a hydraulic lift two pistons are separated by the space filled with a liquid. A piston of small cross-section A₁ is used to exert a force F₁ directly on the liquid. According to Pascals law, the pressure is transmitted through the liquid to a larger piston of area A₂. The upward force exerted on larger piston is

Thus a small force F₁ applied on the smaller piston can be used to exert a large force F₂ on the bigger piston. This is the principle of a hydraulic machine.

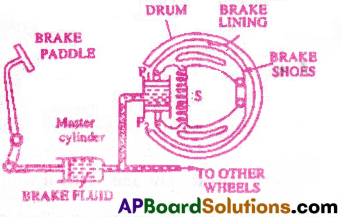
Hydraulic brakes :
When a small force is applied on the pedal with our foot the master piston moves inside the master cylinder. Then the pressure caused is transmitted through the brake oil to act on a piston of larger area.

A large force acts on the piston and is pushed down expanding the brake shoes against brake lining. In this way a small force on the pedal produces a large retarding force on the wheel.

Question 5.
What is hydrostatic paradox? [TS 19]
Answer:
Hydrostatic paradox :
It states that the liquid pressure is same at all points at the same horizontal level (same depth) and is independent of the shape of the container (or) base area.

Illustration of hydrostatic paradox:
Consider three vessels A, B and C of different shapes as shown in figure. They are connected at the bottom by a horizontal pipe.On filling with water, the level in the three vessels is the same, though they hold different amounts of water. This is so because water at the bottom has the same pressure below each section of the vessel.

Question 6.
Explain how pressure varies with depth.
Answer:
Consider a fluid at rest in a container. The pressures at points 1 and 2 are p₁ and p₂ respectively. Consider a cylindrical element of fluid having area of base A and height h. The horizontal forces acting on the cylindrical surface of the fluid column are mutually balanced. Three vertical forces acting on cylindrical element are

1. Force P₁ A acts vertically downwards on the top face of the column.
2. Force P₂A at the bottom face acts vertically upwards.
3. Weight mg of the fluid acts vertically downwards through the centre of gravity of the cylindrical column.

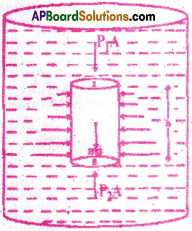
Since the element under consideration is in equilibrium.
∴ ∑F_Y = 0
P₁A + mg – P₂A = 0 (or) (P₂ – P₁)A = mg
If ρ is the density of the fluid then mass of the fluid is m =(Vol) ρ = (Ah)ρ
Then (P₂ – P₁)A = (Ah)ρ g
(or) P₂ – P₁ = hρ g ……… (1)
If the point 1 is shifted to the top of the fluid which is open to the atmosphere then P₁ = P_a = Atmospheric pressure and we may replace p₂ by p.
Then equ(1) gives P – P_a = hpg (or) P = P_a + hρg ………. (2)
Thus the pressure at a point inside a fluid increases with the depth from the free surface.

Question 7.
What is Torricelli’s law? Explain how the speed of efflux is determined with an experiment.
Answer:
Torricelli’s Law :
The efflux velocity of a liquid through an orifice (small hole) of a vessel is equal to the velocity acquired by a freely falling body from a height which is equal to that of liquid level from the orifice.

Let P₁, v₁ and h₁ be the pressure, velocity and height of liquid level at the surface of the liquid.
Let P₂, v₂ and h₂ be the corresponding values at the orifice.
Let ‘ρ‘ be the density of the liquid.

According to Bernoulli’s equation

Question 8.
What is Venturi meter? Explain how it is used. [Imp.Q]
Answer:
The Venturi-meter is a device used for measuring the speed of incompressible fluid How. The Venturi meter consists of a tube with a broad diameter and a small constriction at the middle. A manometer in the form of a U-tube is also attached to it with one arm at the broad neck point of the tube and the other at constriction as shown in figure. The manometer contains a liquid (mercury) of density ρ_m. Let A₁, P_1, and V₁ be the cross-sectional area, fluid pressure and speed of fluid at the broad neck respectively. Let A₂, P_2, and V₂ be the cross-sectional area, fluid pressure and speed of fluid at the constriction respectively.
According to equation of continuity

Question 9.
What is Reynold’s number? What is it’s significance? [Imp.Q]
Answer:
Reynolds number is a dimensionless number which determines the type of flow of liquid through a pipe.

Significance:

1. For a laminar flow the value of Reynold’s number less than 1000.
2. For values of R_C greater than 2000, the flow will be turbulent.
3. For values of R_C lies between 1000 and 2000 the flow is unstable and switches from laminar flow to turbulent and vice-versas.
4. Reynolds number gives the ratio of inertial force and viscous force for a fluid in motion.
5. It has been found that geometrically similar flows become turbulent at the same critical value of R_C. This fact permits us to set up small scale laboratory model to study the character of fluid flow as well as to design ships, submarines, racing cars and aeroplanes.

Question 10.
Explain dynamic lift with example.
Answer:
Dynamic Lift :
Dynamic lift is the force that acts on a body by virtue of its motion through a fluid.

Lift on aircraft wing:

1. The wings of the aeroplane are designed in such a way that the streamlines are clustered on the upper side giving rise to a low pressure.
2. The wing has a curved part on the upper surface as shown in figure
3. As the aeroplane moves fast on the runway, the velocity of air is more at the upper surface of the wings than at its bottom.
4. According to Bemoullis principle, the pressure is less on the upper surface of wing and more on the bottom. The difference in pressure produces the required dynamic lift and allows the aeroplane to take off.

Question 11.
Explain surface tension and surface energy. [Imp. Q]
Answer:
Surface Tension :
The tangential force per unit length, acting at right angles on either side of a line, imagined to be drawn on the free liquid surface in equilibrium is called surface tension of the liquid.

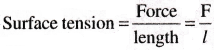
C.G.S Unit: dyne/cm
S.I Unit: N/m
Dimensional formula: [ML°T^-2]

Surface energy :
The amount of work done against the force of surface tension in increasing the liquid surface of a given area at a constant temperature is called the “surface energy”.
Surface Energy E = \(\frac{W}{A}\) S.I. unit = Joule/m²

Question 12.
Explain how surface tension can be measured experimentally.
Answer:

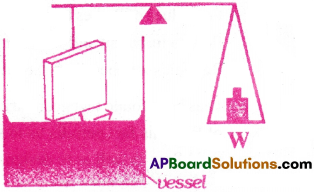
1. The experimental arrangement to measure the surface tension of the liquid-air interface is as shown in figure.
2. A flat vertical glass plate is suspended from one arm of the balance just above the liquid in a vessel.
3. The plate is balanced by weights on the other side, so that horizontal edge of the glass plate just over the liquid.
4. The vessel is slightly raised till the liquid just touches the glass plate.
5. Then the glass plate is pulled down a little because of surface tension.
6. Weights are added till the plate just clear water. If additional weight required is W then the surface tension of the liquid-air interface is
   T = \(\frac{W}{2l}=\frac{mg}{2l}\)
   Where ‘m’ is the extra mass and 7’ is the length of the glass plate edge.

Long Answer Questions

Question 1.
State Bernoulli’s principle. From conservation of energy in a fluid flow through a tube arrive Bernoulli’s equation. Give an application of Bernoulli’s theorem. [AP 15]
Answer:
Bernoulli’s Principle :
For an ideal fluid flow, the total energy( the sum of the pressure energy, kinetic energy, and potential energy) per unit volume of the fluid remains constant at all points in the path of the flow.

The Bernoulli’s equation: \(\frac{\mathrm{P}}{\rho}\) + gh + \(\frac{1}{2}\)v² = Constant.

Consider a nonviscous and incompressible fluid flowing steadily in a tube of non-uniform cross-section.

The liquid enters the tube at the end ‘A’ of cross sectional area ‘A₁‘ at a height ‘h₁‘ with a velocity ‘v₁’, and leaves the tube at narrow end ‘B’ of cross sectional area A₂, at a height h₂, with a velocity v₂.

The mass of the fluid entering into the tube = The mass of the fluid leaving the tube.
⇒ m = ρ₁A₁v₁dt = ρ₂A₂v₂dt
Fluid is incompressible ρ₁ = ρ₂ = ρ
According to equation of continuity A₁v₁ = A₂v₂ = \(\frac{\mathrm{m}}{\rho}\) ……. (1)

Pressure Energy :
Work done on the fluid due to pressure energy at A = P₁A₁v₁
Work done on the fluid due to pressure energy at B = P₂A₂v₂
Net work done due to pressure difference per second = P₁A₁v₁ – P₂A₂v₂ = P₁\(\frac{\mathrm{m}}{\rho}\) – P₂\(\frac{\mathrm{m}}{\rho}\) ……… (2)

Kinetic Energy Kinetic energy of the liquid per second at A = \(\frac{1}{2}\)mv₁²
Kinetic energy of the liquid per second at B = \(\frac{1}{2}\)mv₂²
∴ Gain in Kinetic energy = \(\frac{1}{2}\)m(v₂² – v₁²) ………….. (3)

Potential Energy :
Potential energy of the liquid per second at A = mgh₁
Potential energy of the liquid per second at B = mgh₂
Loss in Potential energy per second = mgh₁ – mgh₂ ……… (4)
According to law of conservation of energy
Loss in Potential Energy + Loss in Pressure Energy = Gain in Kinetic Energy

Application of Bernoulli’s theorem: [TS 15]
Dynamic Lift on air foil (or) an air craft :
An air foil or an air craft wing has a cross-sectional shape which has concave shape at the bottom.

According to Bernoulli’s equation, the pressure above the wings becomes less than the pressure below the wings. Due to this pressure difference, aeroplane is lifted up.

Dynamic Lift on a spinning ball :
Let a ball moves with certain velocity (v) in air. Stream lines are formed due to its spins.

According to Bernoulli’s principle, if the velocity of the fluid is high, the pressure is low, and vice versa. Here the pressure at the top is less when compared with at the bottom of the ball. Here the net upward force acting on the ball is called Dynamic lift.

Question 2.
Define coefficient of viscosity. Explain Stoke’s law and explain the conditions under which a raindrop attains terminal velocity. Give the expression for terminal velocity.
Answer:
Coefficient viscosity :
The coefficient of viscosity is defined as the tangential force per unit area of the layer required to maintain unit velocity gradient.
η = \(\frac{(\mathrm{F} / \mathrm{A})}{\left(\frac{\mathrm{dV}}{\mathrm{dx}}\right)}\)

Stoke’s Law :
According to Stoke’s law, the viscous force (F) acting on a small spherical body moving in a fluid is directly proportional to
i) coefficient of viscosity of fluid(η)
(ii) radius of the spherical body(r)
iii) velocity of the body(V) i.e., F_v ∝ ηrv
It can be derived using dimensional analysis (or) F_v = Kη^ar^bv^c.
[MLT^-2] = K(ML^-1T^-1)^a(L)^b(LT^-1)^C (or) F_v = Kηrv
Where K is a proportionality constant.
Experimentally, the value of K was found to be 6π.
Hence, F_v = 6πηrv
This relation is known as Stoke’s law.

Expression for Terminal velocity :
Consider a spherical raindrop of radius ‘r’ and density p falling under gravity through a fluid of density ρ₀
Now the forces acting on the raindrop are

i) Weight of the drop (W) acting downward W = \(\frac{4}{3}\)πr³ρg …………. (1)
ii) Force of buoyancy (F_B) acting upward F_B = \(\frac{4}{3}\)πr³ ρ₀g ……….. (2)
iii) Viscous force of the fluid (F_v) acting upward
F_v = 6πηrv (According to Stoke’s law)
InitiallyW > F_B + F_v and the spherical rain drop keeps on falling with acceleration
a = \(\frac{W-(F_v+F_B)}{m}\)
Where ‘m’ is the mass of the sphere.
The sphere continuously gains velocity which results in increase in the value of F_v.
For a given value of F_v we get W = F_B + F_v
The resultant force then becomes zero and the spherical raindrop acquires constant velocity which is known as terminal velocity.

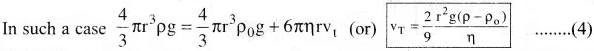
Solved Problems

Question 1.
What is the pressure on a swimmer 10m below the surface of a lake?(Take g = 10ms^-2)
Solution:
Pressure P = P_a + pρh
Here P_a = 1.01 × 10⁵ Pa, h = 10 m, ρ = 1000 kgm^-3
P = 1.01 × 10⁵ + 1000 × 10 × 10 = 2.01 × 10⁵ Pa ≅ 2 atm

Question 2.
The density of the atmosphere at sea level is 1.29 kg/m³. Assume that it does not change with altitude. Then how high would the atmosphere extend?
Solution:
P_a = ρgh
Here P_a = 1.01 × 10⁵ Pa, g = 9.8 m/s², ρ = 1.29 kg/m³.
1.01 × 10⁵ = 1.29 × 9.8 × h

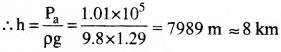
Question 3.
Two syringes of different cross sections and lengths filled with water are connected with a tightly fitted rubber tube filled with water. Diameters of the smaller piston and larger piston are 1 cm and 3 cm respectively. Find the force exerted on the larger piston when a force of 10 N is applied to the smaller piston.
Solution:

Question 4.
Sn a car lift compressed air exerts a force F₁ on a small piston having a radius of 5.0 cm. This pressure is transmitted to a second piston of radius 15cm. If the mass of the car to be lifted is 1350 kg. Calculate F₁. What is the pressure necessary to accomplish this task? (g = 9.8 ms^-2)
Solution:
Since pressure is transmitted undiminished throughout the fluid,

This is almost double the atmospheric pressure.

Exercise Problems

Question 1.
Calculate the work done in blowing a soap bubble of diameter 0.6cm against the surface tension T . (Surface tension of soap solution = 2.5 × 10^-2 Nm^-1)
Solution:
Given surface tension T =2.5 × 10^-2 Nm^-1
Diameter of at soap bubble = 0.6cm = 0.6 × 10^-2m
⇒ Radius of soap bubble r = 0.3 × 10^-2m.
Workdone W = 8πr²T = 8 × 3.14 × (0.3 × 10^-2)² × 2.5 × 10^-2 = 5.652 × 10^-6 joule.

Question 2.
How high does methyl alcohol rise in a glass tube of diameter 0.06 cm? (Surface tension of methyl alcohol = 0.023 Nm^-1 and density = 0.8 gmcm^-3. Assume that the angle of contact is zero)
Solution:

Question 3.
What should be the radius of a capillary tube, if the water has rise the height of 6cm in it? Surface tension of water = 7.2 × 10^-2N/m, g = 10m/sec². [May 2010]
Solution:

Question 4.
Find the depression of the meniscus in the capillary tube of diameter 0.4 mm dipped in a beaker containing mercury. (Density of mercury = 13.6 × 10³kg m^-3 and surface tension of mercury = 0.49 Nm^-1 and angle of contact = 135°)
Solution:
Diameter of the capillary tube = 0.4mm = 0.4 × 10^-3m.
⇒ Radius of the capillary tube r = 0.2 × 10^-3m.
Density of mercury ρ = 13.6 × 10³kg/m
Surface tension T = 0.49 Nm^-1
Angle of contact θ = 135°m

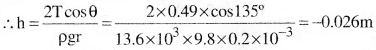
Question 5.
If the diameter of a soap bubble is 10 mm and its surface tension is 0.04 Nm^-1, find the excess jpressure inside the bubble. [AP 15][TS 16,18]
Solution:
Given r = 5 mm = 5 × 10^-3 m,
T = 0.04 Nm^-1
The excess pressure inside the bubble P = \(\frac{4T}{r}\)
∴ P = \(\frac{4 \times 0.04}{5 \times 10^{-3}}\) = 32Nm^-2

Question 6.
If work done by an agent to form a bubble of radius R is W, then how much energy is required to increase its radius to 2R?
Solution:
Work done to form a bubble W = 2(4πR²)T
Energy required to increase its radius to 2R is
W¹ =8rfT(R²₂ – R²₁)
= 8πT[(2R)² – R²] = 3[8πR²T] = 3W

Question 7.
If two soap bubbles of radii R₁ and R₂ (in vacuum) coalesce under isothermal conditions, what is the radius of the new bubble. Take T as the surface tension of soap solution.
Solution:
Work done in forming a soap bubble of radius, R₁ is W₁ = 8nR²₁T
Word done in forming a soap bubble of radius R₂ is W₂ = 8πR²₂T
Total work done w = W₁ + W₂ = 8πR²₁T + 8πR²₂T = 8π(R²₁ + R²₂)T
If the radius of bubble after merging is R then the work done in forming a soap bubble of radius R is W = 8πR²T

Multiple Choice Questions

Question 1.
If the surface tension of a soap water is 0.04 Nm^-1. The excess pressure inside a 10mm diameter soap bubble in Nm^-2 will be
1) 4
2) 16
3) 8
4) 32
Answer:
4) 32

Question 2.
The rise of a liquid due to surface tension in a narrow capillary tube of diameter’d’ is ‘h’. If the diameter is reduced to d/2 the rise will be
1) h
2) 2h
3) h/2
4) h/3
Answer:
2) 2h

Question 3.
If the surface tension of water is 73 × 10^-2Nm^-1, the excess pressure inside a spherical drop of water of radius 1mm is …… N/m²
1) 14
2) 7.3
3) 41
4) 7 × 10^-2
Answer:
1) 14

Question 4.
The angle of contact between pure water and clean glass is
1) 90°
2) 0°
3) 15°
4) 137°
Answer:
2) 0°

Question 5.
If temperature of a liquid is increased, then its surface tension in gerteral
1) decreases
2) increases
3) remaining the same
4) increasing and then decreases
Answer:
1) decreases

Question 6.
Surface tension arises due to
1) adhesive molecule forces
2) cohesive molecular forces
3) gravitational forces
4) molecular forces
Answer:
2) cohesive molecular forces

Question 7.
8000 identical water drops are combined to from a big drop. Then the ratio of final surface energy to the initial surface energy of all the drops together is
1) 1 : 10
2) 1 : 15
3) 1 : 20
4) 1:25
Answer:
3) 1 : 20

Question 8.
The surface energy of liquid film on a ring of area 0.15m²is (surface tension of liquid is equal to 5Nm^-1)
1) 0.75J
2) 1.5J
3) 2.25J
4) 3.0J
Answer:
2) 1.5J

Question 9.
A mercury drop of radius lcm is sprayed into 10⁶ drops of equal size, the energy expended in joules is (surface tension of mercury is 460 × 10^-3Nm^-1)
1) 0.057
2) 5.7
3) 5.7 × 10^-4
4) 5.7 × 10^-6
Answer:
1) 0.057

Question 10.
The work done increasing the size of a rectangular soap film with dimensions 8cm × 3.75cm to 10 cm × 6cm is 2 × 10^-4 J. The surface tension of the film in Nm^-1 is
1) 1.65 × 10^-2
2) 3.33 × 10^-2
3) 6.6 × 10^-2
4) 8.25 × 10^-2
Answer:
2) 3.33 × 10^-2

Question 11.
Drops of liquid of density ’d’ are floating half immersed in a liquid of density ρ. If the surface tension of the liquid is T, then the radius of the drop is

Answer:
3

Question 12.
Two soap bubbles are blown. In the first soap bubble excess pressure is 4 times of the second soap bubble. The ratio of radii of the first and .Second soap bubble is
1) 1 : 4
2) 1 : 2
3) 2 : 1
4) 4 : 1
Answer:
1) 1 : 4

Question 13.
An aeroplane of mass 3 × 10⁴kg and total wing area 120m² is in a level flight at some height. The difference in pressure between the upper and lower surfaces of its wings in kilo pascal is (g = 10m/s²)
1) 2.5
2) 5.0
3) 10.0
4) 12.5
Answer:
1) 2.5

Question 14.
The speed of air flow on the upper and lower surface of wing of an aeroplane V₁ and V₂ respectively. If A is the area of cross-section of the wire and p is the density of air, then the upward lift is

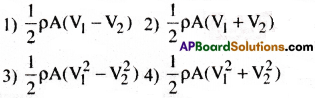
Answer:
3

Question 15.
Water in a river 20m deep is flowing at a speed of 10ms^-1. The shearing stress between the horizontal layers of water in the river in Nm^-2, is (coefficient of viscosity of water = 10^-3 SI units)
1) 1 × 10^-2
2) 0.5 × 10^-2
3) 1 × 10^-3
4) 0.5 × 10^-3
Answer:
4) 0.5 × 10^-3

Question 16.
A large tank filled with water to a height ’h’ is to be emptied through a small hole at the bottom. The ratio of times taken for the level of water to fall from h to h/2 and from h/2 to zero is

Answer:
3

Question 17.
A cylinder of weight 20m is completely filled with water. The velocity of efflux of water in (in ms^-1) through a small hole on the side wall of the cylinder near its bottom is
1) 10 ms^-1
2) 20 ms^-1
3) 25.5 ms^-1
4) 5 ms^-1
Answer:
2) 20 ms^-1

Question 18.
A rectangular film of liquid is extended from (4 cm × 2 cm) to (5 cm × 4 cm). If the work done is 3 × 10^-4J, the value of the surface tension of the liquid is
1) 0.250 Nm^-1
2) 0.125 Nm^-1
3) 0.2 N m^-1
4) 8.0 Nm^-1
Answer:
2) 0.125 Nm^-1

Question 19.
A capillary tube of radius r is immersed in water and water rises in it to a height h. The mass of the water in the capillary is 5g. Another capillary tube of radius 2r is immersed in water. The mass of water that will rise in this tube is
1) 2.5 g
2) 5.0 g
3) 10.0 g
4) 20.0 g
Answer:
3) 10.0 g

Question 20.
A small hole of area of cross-section 2 mm² is present near the bottom of a fully filled open tank of height 2 m. Taking g = 10 m/s², the rate of flow of water through the open hole would be nearly
1) 6.4 × 10^-6m³/s
2) 12.6 × 10^-6 m³/s
3) 8.9 × 10^-6m³/s
4) 2.23 × 10^-6 m³/s
Answer:
2) 12.6 × 10^-6 m³/s

Question 21.
The cylindrical tube of a spray pump has radius R, one end of which has n fine holes, each of radius r. If the speed of the liquid in the tube is V, the speed of the ejection of the liquid through the holes is

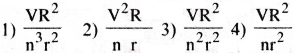
Answer:
4

Question 22.
The wettability of a surface by a liquid depends primarily on
1) density
2) angle of contact between the surface and the liquid
3) viscosity
4) surface tension.
Answer:
2) angle of contact between the surface and the liquid

Question 23.
Water rises to a height h in capillary tube. If the length of capillary tube above the surface of water is made less than h, then
1) water rises upto a point a little below the top and stays there
2) water does not rise at all
3) water rises upto the tip of capillary tube and then starts overflowing like a fountain
4) water rises upto the top of capillary tube and stays there without overflowing.
Answer:
3) water rises upto the tip of capillary tube and then starts overflowing like a fountain

Question 24.
Terminal velocity of a liquid drop of radius ‘r’ falling through air is V. If two such drops are combined to form a bigger drop, the terminal velocity with which the bigger drop falls through air is (Ignore buoyant force due to air)]

Answer:
3