AP Inter 1st Year Maths 1B Question Paper March 2023

by

Access to a variety of AP Inter 1st Year Maths 1B Model Papers and AP Inter 1st Year Maths 1B Question Paper March 2023 allows students to familiarize themselves with different question patterns.

AP Inter 1st Year Maths 1B Question Paper March 2023

Time : 3 Hours
Max. Marks : 75

Section – A
(10 × 2 = 20)

I. Very Short Answer Type Questions.

  1. Answer all questions.
  2. Each question carries two marks.

1. Find the distance between parallel lines 5x – 3y – 4 = 0 and 10x – 6y – 9 = 0.

2. Show that the points A(3, 2, -4), B(5, 4, -6) and C(9, 8, -10) are collinear.

3. Write the equation of plane 4x – 4y + 2z + 5 = 0 in intercepts form.

AP Inter 1st Year Maths 1B Question Paper March 2023

4. If the increase in side of square is 4%, then find the approximate percentage of increase in the area of square.

5. Transform the equation \(\sqrt{3}\)x + y + 10 = 0 into

  1. slope- intercept form
  2. normal form.

6. Find the second order derivative of y = tan-1\(\left(\frac{2 x}{1-x^2}\right)\).

7. Find the derivative of e2x.log (3x + 4) (x > \(\frac{-4}{3}\))

8. Verify Rolle’s theorem for the function f(x) = x2 – 1 on [-1, 1]

9. Compute \(\lim _{x \rightarrow 2^{+}}\)([x] + x) and \(\lim _{x \rightarrow 2}\) ([x] + x).

Section – B
(5 × 4 = 20)

II. Short Answer Type Questions.

  1. Answer ANY FIVE questions.
  2. Each question carries FOUR marks.

11. If f, given by
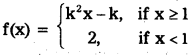
AP Inter 1st Year Maths 1B Question Paper March 2023 1
is a continuous function on R, then find values of k.

12. Find the derivative of ‘sec 3x’ from the first principle.

13. The volume of a cube is increasing at the rate of 8 cm3/sec. How fast is the surface area increasing when the length of an edge is 12 cm ?

14. Find the lengths of normal and sub-normal at a point on the curve
y = \(\frac{a}{2}\left(e^{x / a}+e^{-x / a}\right)\).

15. Find the equation of locus of ‘P’, if the ratio of distances from P to A(5, -4) and B(7, 6) is 2 : 3.

AP Inter 1st Year Maths 1B Question Paper March 2023

16. When the axes are rotated through an angle, find the transformed equation of 3x2 + 10xy + 3y2 = 0.

17. Find the point on the straight line 3x + y + 4 = 0 which is equidistant from the points (-5, 6) and (3, 2).

Section – C
(5 × 7 = 35)

III. Long Answer Type Questions.

  1. Answer ANY FIVE questions.
  2. Each question carries SEVEN marks.

18. Find the orthocentre of triangle formed by the lines x + 2y = 0, 4x + 3y – 5 = 0 and 3x + y = 0.

19. Find the angle between the lines joining the origin to the points of intersection of the curve x2 + 2xy + y2 + 2x + 2y – 5 = 0 and the line 3x – y + 1 = 0.

20. Show that the area of triangle formed by the lines ax2 + 2hxy + by2 = 0 and lx + my + n = 0 is \(\left|\frac{n^2 \sqrt{h^2-a b}}{a m^2-2 h l m+b l^2}\right|\)

21. Find the angle between the lines whose direction cosines are given by the equations 3l + m + 5n = 0 and 6mn – 2nl + 5lm = 0.

AP Inter 1st Year Maths 1B Question Paper March 2023

22. If xy + yx = ab, then show that \(\frac{d y}{d x}\) = –\(\left(\frac{y \cdot x^{y-1}+y^x \cdot \log y}{x^y \log x+x \cdot y^{x-1}}\right)\).

23. If the tangent at any point on the curve x2/3 + y2/3 = a2/3 intersects the co-ordinate axes in A and B, then show that the length AB is a constant.

24. The profit function P(x) of a company selling x items per day is given by P(x) = (150 – x) x – 1000. Find the number of items that the company should manufacture to get maximum profit. Also find the maximum profit.

Leave a Comment