AP Inter 1st Year Maths 1B Question Paper March 2018

Access to a variety of AP Inter 1st Year Maths 1B Model Papers and AP Inter 1st Year Maths 1B Question Paper March 2018 allows students to familiarize themselves with different question patterns.

AP Inter 1st Year Maths 1B Question Paper March 2018

Time : 3 Hours
Max. Marks : 75

Note : This question paper consists of THREE sections A, B and C.

Section – A
(10 × 2 = 20 Marks)

I. Very short answer type questions :

1. Answer all the questions.
2. Each question carries two marks.

Question 1.
Find the value of x, if the slope of the line passing through (2, 5) and (x, 3) is 2.
Solution:
Given the slope of the line passing through (2, 5) and (x, 3) is 2
⇒ \(\frac{3-5}{x-2}\) = 2
⇒ -2 = 2x – 4
⇒ 2x = 2 ⇒ x = 1

Question 2.
Find the sum of the squares of the intercepts of the line 4x – 3y = 12 on the axes of co-ordinates.
Solution:
Given line equation is 4x – 3y = 12
⇒ \(\frac{4 x}{12}-\frac{3 y}{12}\) = 1
⇒ \(\frac{x}{3}+\frac{y}{-4}\) = 1
a = X – intercept = 3
b = Y – intercept = – 4
a² + b² = 3² + (-4)² = 9 + 16 = 25

Question 3.
Show that the points (1, 2, 3), (2, 3, 1) and (3, 1, 2) form an equilateral triangle.
Solution:
Let A = (1, 2, 3)
B = (2, 3, 1)
C = (3, 1, 2)

Question 4.
Find the intercepts of the plane 4x + 3y – 2z + 2 = 0 on the co-ordinate axes.
Solution:
Given plane equation is 4x + 3y – 2z + 2 = 0
⇒ 4x + 3y – 2z = – 2
⇒ \(\frac{4 x}{-2}\) + \(\frac{3 y}{-2}\) – \(\frac{2 z}{-2}\) = \(\frac{-2}{-2}\)
⇒ \(\frac{x}{\frac{-1}{2}}+\frac{y}{\frac{-2}{3}}+\frac{z}{1}\) = 1
∴ X-intercept = \(\frac{-1}{2}\)
Y-intercept = \(\frac{-2}{3}\)
Z-intercept = 1.

Question 5.
Compute \(\lim _{x \rightarrow 0} \frac{e^{3 x}-1}{x}\)
Solution:

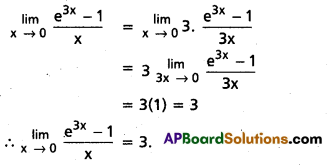
Question 6.
Compute \(\lim _{x \rightarrow \infty} \frac{11 x^3-3 x+4}{13 x^3-5 x^2-7}\)
Solution:

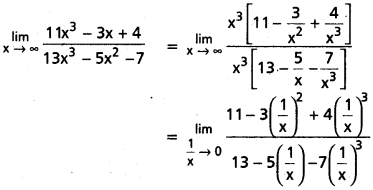
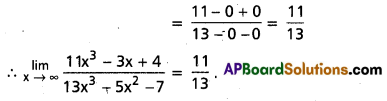
Question 7.
If f(x) = sin (log x), (x > 0) then find f'(x).
Solution:
Given f(x) = sin (log x)
differentiating w.r. to ’x’ on both sides, we have
f'(x) = cos (log x) \(\frac{d}{d x}\)(log x) dx
= cos (log x). \(\frac{1}{x}\).
∴ f'(x) = \(\frac{\cos (\log x)}{x}\)

Question 8.
If y = x⁴ + tan x then find y”.
Solution:
Given y = x⁴ + tan x
y’ = 4x³ + sec²x
y” = 4(3x²) + 2 sec x \(\frac{d}{d x}\) (sec x)
= 12x² + 2 sec x (sec x tan x)
= 12x² + 2 sec² x tan x.

Question 9.
If the increase in the side of a square is 4% then find the approximate percentage of increase in the area of the square.
Solution:
Let x, A be the side and area of a square respectively.
Given \(\frac{\Delta x}{x}\) × 100 = 4
A = x²
∆A = 2x ∆x
\(\frac{\Delta \mathrm{A}}{\mathrm{A}}\) × 100 = \(\frac{2 x \Delta x}{x^2}\) × 100
= 2 \(\frac{\Delta x}{x}\) × 100 = 2(4) = 8.
∴ The approximate increase in the area is 8 %.

Question 10.
Verify Rolle’s theorem for the function f(x) = x(x + 3) e^-x/2 in [-3, 0].
Solution:
Given f(x) = x(x + 3) e^-x/2
= (x² + 3x) e^-x/2
f is continuous on [-3, 0] and f is derivable on (-3, 0)
Also f(- 3) = 0 = f(0)
∴ f satisfies all the conditions of Roll’s Theorem.
∴ There exists c ∈ (- 3, 0) such that f'(c) = 0

⇒ -c² + c + 6 = 0
⇒ c² – c – 6 = 0
⇒ c² – 3c + 2c – 6 = 0
⇒ c(c – 2) + 2(c – 3) = 0
⇒ (c + 2)(c – 3) = 0
⇒ c = -2, 3
since c ∈ (-3, 0)
∴ c = -2 ∈ (-3, 0)
Hence Rolle’s theorem is verified.

Section – B
(5 × 4 = 20 Marks)

II. Short Answer Type Questions :

1. Attempt any five questions.
2. Each question carries four marks.

Question 11.
Find the equation of the locus of P, if A = (2, 3), B = (2, – 3) and PA + PB = 8.
Solution:
Given A = (2, 3)
B = (2, -3)
Let P(x, y) be any point on the locus.
Given geometric condition is PA + PB = 8

Question 12.
When the origin is shifted to (-1, 2) by the translation of axes, find the transformed equation of x² + y² + 2x – 4y + 1 = 0.
Solution:
Given equation is x² + y² + 2x – 4y + 1 = 0 ………… (1)
Here (h, k) = (-1, 2)
x = x + h = x – 1
y = y + k = y + 2
Required transformed equation is
(x – 1)² + (y + 2)² + 2(x – 1) – 4(y + 2) + 1 = 0
⇒ x² – 2x + 1 + y² + 4y + 4 + 2x – 2 – 4y – 8 + 1 = 0
⇒ x² + y² – 4 = 0

Question 13.
Show that the lines 2x + y – 3 = 0, 3x + 2y – 2 = 0 and 2x – 3y – 23 = 0 are concurrent and find the Point of concurrency.
Solution:
Given lines are 2x + y – 3 = 0 ……. (1)
3x + 2y – 2 = 0 ……. (2)
2x – 3y – 23 = 0 ………. (3)
solving (1) and (2)

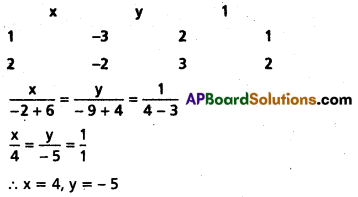
From (3)
2x – 3y – 23 = 2(4) – 3(-5) – 23
= 8 + 15 – 23
= 23 – 23 = 0
The point (4, -5) lies on (3)
∴ (1), (2), (3) are concurrent.
Point of concurrency = (4, -5).

Question 14.
Find the real constants a, b so that the function f given by

is continuous on R.
Solution:
Given f(x) = sin x, if x ≤ 0
= x² + a, if 0 < x < 1 = bx + 3, if 1 ≤ x ≤ 3 = -3, if x > 3

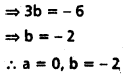
Question 15.
Find the derivative of the function sin 2x from the first Principle.
Solution:
Let f(x) = sin 2x
By first principle

Question 16.
A particle is moving along a line according to S = f(t) = 4t³ – 3t² + 5t – 1 where S is measured in metres and t is measured in seconds. Find the velocity and acceleration at time t. At what time the acceleration is zero ?
Solution:
Given s = f(t) = 4t³ – 3t² + 5t – 1
Velocity \(\frac{\mathrm{ds}}{\mathrm{dt}}\) = 4(3t²) – 3(2t) + 5(1) – 0 = 12t² – 6t + 5
Acceleration \(\frac{d^2 s}{d^2}\) = 12(2t) – 6(1) + 0 = 24t – 6
\(\frac{d^2 s}{d t^2}\) = 0 ⇒ 24t – 6 = 0
⇒ 24t = 6
⇒ t = \(\frac{1}{4}\)
∴ Acceleration is zero when t = \(\frac{1}{4}\) sec.

Question 17.
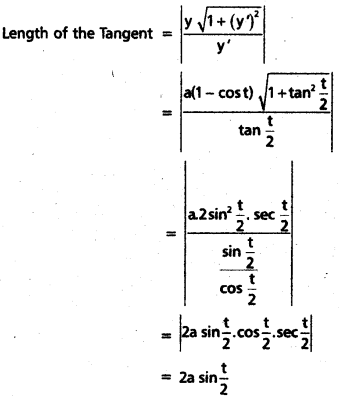
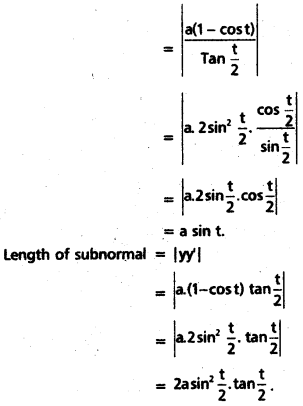
At any point t on the curve x = a(t + sin t); y = a(1 – cos t), find the lengths of tangent, normal, subtangent and subnormal.
Solution:
Given x = a(t + sin t)
differentiating w. r. to on bothsides, we have
\(\frac{d y}{d t}\) = a(1 + cos t)
Given y = a(1 – cost)
differentiating w.r. to ‘t’ on bothsides, we have

Section – C

III. Long Answer Type Questions :

1. Attempt any five questions.
2. Each question carries seven marks.

Question 18.
Find the circumcentre of the triangle whose vertices are(1, 3), (0, – 2) and (- 3, 1).
Solution:
Let A = (1, 3)
B = (0, -2)
C = (-3, 1)
Let S(α, β) be the circumcentre of the ∆ABC
∴ SA = SB = SC
SA = SB
\(\sqrt{(\alpha-1)^2+(\beta-3)^2}\) = \(\sqrt{(\alpha-0)^2+(\beta+2)^2}\)
⇒ (α – 1)² + (β – 3)² = α² + (β + 2)²
⇒ α² – 2α + 1 + β² – 6β + 9 = α² + β² + 4β + 4
⇒ 2α + 10β – 6 = 0
⇒ α + 5β – 3 = 0 ….. (1)
SB = SC
⇒ \(\sqrt{(\alpha-0)^2+(\beta+2)^2}\) = \(\sqrt{(\alpha+3)^2+(\beta-1)^2}\)
⇒ α² + (β + 2)² = (α + 3)² + (β – 1)²
⇒ α² + β² + 4β + 4 = α² + 6α + 9 + β² – 2β + 1
⇒ 6α – 6β + 6 = 0
⇒ α – β = 0 …… (2)
Solving (1) and (2)

Question 19.
If the equation ax² + 2hxy + by² = 0 represents a pair of intersecting lines then prove that the combined equation of the pair of bisectors of the angles between these lines is h(x² – y²) = (a – b)xy.
Solution:
Since the straight lines represented by the given equation pass through the origin, their separate equation pass through the origin, their separate equations (in symmetric form) can be taken as
x sin θ – y cos θ = 0 and x sin φ – y cos φ = 0.
H ≡ ax² + 2hxy + by²
≡ λ(x sin θ – y cos θ) (x sin φ – y cos φ)
for some real λ ≠ 0. From this, we obtain
sin θ sin φ = \(\frac{a}{\lambda}\), cos θ cos φ = \(\frac{b}{\lambda}\) and sin (θ + φ) = \(\frac{-2 h}{\lambda}\) …….. (1)
The equations of the straight lines bisecting the angles between the given pair of lines is therefore
(x sin θ – y cos θ) ± (x sin φ – y cos φ) = 0
Accordingly, their combined equation is

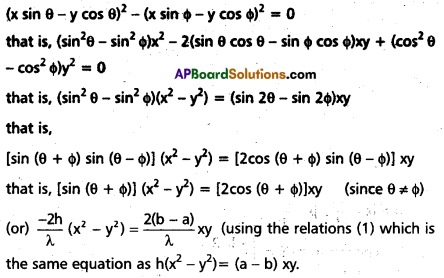
Question 20.
Find the angle between the straight lines joining the origin to the points of intersection of the curve 7x² – 4xy + 8y² + 2x – 4y – 8 = 0 with the straight line 3x – y = 2.
Solution:
Given curve equation is 7x² – 4xy + 8y² + 2x – 4y – 8 = 0 ……… (1)
Given line equation is 3x – y = 2
⇒ \(\frac{3 x-y}{2}\) = 1 ………. (2)
Homoginising (1) with the help of (2)
Combined equation of OA, OB is 7x² – 4xy + 8y² + 2x.1 – 4y.1 – 8.1² = 0

Question 21.
Find the direction cosines of two lines which are connected by the relations l – 5m + 3n = 0 and 7l² + 5m² – 3n² = 0.
Solution:
Given l – 5m + 3n = 0 ⇒ l = 5m – 3n …….. (1)
7l² + 5m² – 3n² = 0 ……… (2)
Eliminating ‘l’ from (1) and (2)
7(5m – 3n)² + 5m² – 3n² = 0
⇒ 7(25m² – 30mn + 9n²) + 5m³² – 3n² = 0
⇒ 175m² – 210mn + 63n² + 5m² – 3n² = 0
⇒ 180m² – 210mn + 60n² = 0
⇒ 6m² – 7mn + 2n² = 0
⇒ 6m² – 4mn – 3mn + 2n² = 0
⇒ 2m(3m – 2n) – n(3m – 2n) = 0
⇒ (3m – 2n) (2m – n) = 0
⇒ 3m – 2n = 0 ……….. (3)
⇒ 2m – n = 0 …….(4)
From (3), (1)

Question 22.
If y = x^{tan x} + (sin x)^{c0s x}, find \(\frac{\mathrm{dy}}{\mathrm{dx}}\).
Solution:
Given y = xtanx + (sinx)c0SX
Let u = xtan x and v = (sin x)cos x
log u = tan x. log x
\(\frac{1}{u} \cdot \frac{d u}{d x}\) = tanx.\(\frac{1}{x}\) + log x.sec²x

Question 23.
Find the angle between the curves y² = 8x, 4x² + y² = 32.
Solution:
Given curve equations are y² = 8x ……… (1)
4x² + y² = 32 …… (2)
From (1) & (2)
4x² + 8x = 32
⇒ x² + 2x = 8
⇒ x2 + 2x – 8 = 0
⇒ (x + 4)(x – 2) = 0
⇒ x = -4, 2
If x = 2 then y² = 16
⇒ y = ±4
The point of intersection of (1) & (2) are P(2, 4) and Q(2, -4).
Equation of the first curve is y² = 8x
differentiating w.r. to x on both sides, we have

Equation of the second curve is 4x² + y² = 32
differentiating w.r. to ‘x on both sides, we have

Question 24.
Find two positive integers whose sum is 16 and the sum of whose squares is minimum.
Solution:
Let x, y be two positive integers.
Given x + y = 16 ⇒ y = 16 – x
Let S = x² + y²
= x² + (16 – x)²
= x² + 256 – 32x + x²
= 2x² – 32x + 256
\(\frac{\mathrm{ds}}{\mathrm{dx}}\) = 2.2x – 32(1) + 0
\(\frac{\mathrm{ds}}{\mathrm{dx}}\) = 4x – 32
\(\frac{\mathrm{ds}}{\mathrm{dx}}\) = 0 ⇒ 4x – 32 = 0
⇒ 4x = 32
⇒ x = 8
\(\left(\frac{d^2 s}{d x^2}\right)_{x=8}\) = 4.1 – 0 = 4 >0
∴ S has minimum at x = 8
∴ y = 16 – 8 = 8
Hence x = 8, y = 8.