Access to a variety of AP Inter 1st Year Maths 1B Model Papers and AP Inter 1st Year Maths 1B Question Paper April 2022 allows students to familiarize themselves with different question patterns.
AP Inter 1st Year Maths 1B Question Paper April 2022
Time : 3 Hours
Max. Marks : 75
Section – A
(10 × 2 = 20)
I. Very Short Answer Type Questions.
- Answer all questions.
- Each question carries two marks.
1. Transform the equation 3x + 4y + 12 = 0 into
- Slope-intercept form
- intercept form
2. Find the value of p, if the straight lines x + P = 0, y + 2 = 0 and 3x + 2y + 5 = 0 are concurrent.
3. If (3, 2, -1), (4, 1, 1) and (6, 2, 5) are three vertices and (4, 2, 2) is the centroid of a tetrahedron, find the fourth vertex.
![]()
4. Find the equation of the plane whose intercepts on X, Y, Z- axes are 1, 2, 4 respectively.
5. Compute \(\lim _{x \rightarrow 0} \frac{e^x-1}{\sqrt{1+x}-1}\)
6. Compute \(\lim _{x \rightarrow \infty} \frac{8|x|+3 x}{3|x|-2 x}\)
7. If f(x) = sin (log x), (x > 0) find f(x).
8. Find the derivative of cos (log x + ex).
9. Find the slope of the normal to the curve x = a cos3θ, y = a sin3θ at θ = \(\frac{\pi}{4}\).
10. Find the intervals on which f(x) = x2 – 3x + 8 is increasing or decreasing.
Section – B
II. Short answer type questions :
- Attempt any five questions.
- Each question carries four marks.
11. If the distance from P to the points (2, 3) and (2, -3) are in the ratio 2 : 3, then find the equation of the locus of P.
12. A(5, 3) and B(3, -2) are two fixed points. Find the equation of the locus of P, so that the area of triangle PAB is 9.
13. A straight line with slope 1 passes through Q (-3, 5) and meets the straight line x + y – 6 = 0 at P, Find the distance PQ.
![]()
14. If f given by
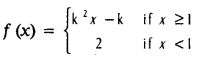
is a continuous function on R, then find the values of k.
15. Find \(\frac{\mathrm{d} y}{\mathrm{~d} x}\) for the function
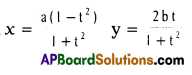
16. Find the angle between the curve 2y = \(e^{\frac{-x}{2}}\) and Y-axis.
17. Show that \(\frac{x}{1+x}\) < In (1 + x)< x, ∀ x > 0.
Section – C
(5 × 7 = 35)
III. Long answer type questions :
- Attempt any five questions.
- Each question carries seven marks.
18. If p and q are the lengths of the perpendiculars from the origin to the straight lines x secα + y cosecα = a and x cosα – y sinα = a cos2α, prove that 4p2 + q2 = a2.
19. Show that the pairs of straight lines 6x2 – 5xy – 6y2 = 0 and 6x2 – 5xy – 6y2 + x + 5y – 1 = 0 form a square.
20. Find the values of k if the lines joining the origin to the points of intersection of the curve 2x2 – 2xy + 3y2 + 2x – y – 1 = 0 and the line x + 2y = k are mutually perpendicular.
21. Find the direction cosines of two lines which are connected by the relations l + m + n = 0 and mn – 2nl – 2lm = 0.
![]()
22. If xy = yy then
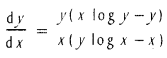
23. Show that the tangent at P(x1, y1) on the curve
= \(\sqrt{x}+\sqrt{y}\) = \(\sqrt{a}\) is
\(y y_1{ }^{\frac{-1}{2}}\) = \(a^{\frac{1}{2}}\)
24. The profit function P(x) of a company, selling x items per day is given by P(x) = (150 – x) x – 1600. Find the number of items that the company should sell for maximum profit. Also find the maximum profit.