AP Inter 1st Year Maths 1A Question Paper May 2019

Thoroughly analyzing AP Inter 1st Year Maths 1A Model Papers and AP Inter 1st Year Maths 1A Question Paper May 2019 helps students identify their strengths and weaknesses.

AP Inter 1st Year Maths 1A Question Paper May 2019

Time: 3 Hours
Maximum Marks: 75

Note: This question paper consists of three sections A, B, and C.

Section – A
(10 × 2 = 20 Marks)

I. Very Short Answer Type Questions.

• Attempt All questions.
• Each question carries Two marks.

Question 1.
If A = {-2, -1, 0, 1, 2} and f: A → B is a surjection defined by f(x) = x² + x + 1, then find B.
Solution:
Given A = {-2, -1, 0, 1, 2} and f(x) = x² + x + 1
f(-2) = (-2)² + (-2) + 1 = 4 – 2 + 1 = 3
f(-1) = (-1)² + (-1) + 1 = 1 – 1 + 1 = 1
f(0) = 0² + 0 + 1 = 0 + 0 + 1 = 1
f(1) = 1² + 1 + 1 = 1 + 1 + 1 = 3
f(2) = 2² + 2 + 1 = 4 + 2 + 1 = 7
Since f: A → B is a surjection.
∴ B = f(A) = {1, 3, 7}

Question 2.
Find the domain of the real-valued function f(x) = \(\sqrt{4 x-x^2}\).
Solution:
Given f(x) = \(\sqrt{4 x-x^2}\)
x ∈ R ⇒ 4x – x² ≥ 0
⇒ x² – 4x ≤ 0
⇒ x(x – 4) ≤ 0
⇒ x ∈ [0, 4]
∴ Domain of f = [0, 4]

Question 3.
If A = \(\left[\begin{array}{cc}
2 & -4 \\
-5 & 3
\end{array}\right]\), then find A + A’ and AA’.
Solution:
Given A = \(\left[\begin{array}{cc}
2 & -4 \\
-5 & 3
\end{array}\right]\)
A’ = \(\left[\begin{array}{cc}
2 & -5 \\
-4 & 3
\end{array}\right]\)

Question 4.
Find the rank of the matrix \(\left[\begin{array}{ccc}
1 & 4 & -1 \\
2 & 3 & 0 \\
0 & 1 & 2
\end{array}\right]\).
Solution:
Let A = \(\left[\begin{array}{ccc}
1 & 4 & -1 \\
2 & 3 & 0 \\
0 & 1 & 2
\end{array}\right]\)
det A = 1(6 – 0) – 2(8 + 1)
= 6 – 18
= -12 ≠ 0
∴ Rank of A = 3

Question 5.
If the position vectors of the points A, B and C are \(-2 \bar{i}+\bar{j}-\bar{k}\), \(-4 \bar{i}+2 \bar{j}+2 \bar{k}\) and \(6 \bar{i}-3 \bar{j}-13 \bar{k}\) respectively and \(\overline{\mathrm{AB}}=\lambda \overline{\mathrm{AC}}\), then find the value of λ.
Solution:

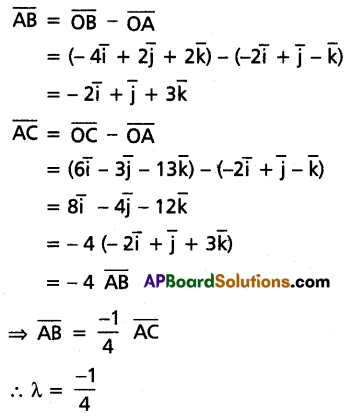
Question 6.
Find the vector equation of the plane passing through the points \(\overline{\mathrm{i}}-2 \overline{\mathrm{j}}+5 \overline{\mathrm{k}},-5 \overline{\mathrm{j}}-\overline{\mathrm{k}}\) and \(-3 \bar{i}+5 \bar{j}\).
Solution:

Question 7.
\(\bar{a}=2 \bar{i}-\bar{j}+\bar{k}, \bar{b}=\bar{i}-3 \bar{j}-5 \bar{k}\), Find the vector \(\bar{c}\) such that \(\bar{a}\), \(\bar{b}\) and \(\bar{c}\) form the sides of a triangle.
Solution:

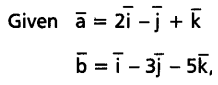
Question 8.
Sketch the graph of the function sin 2x in the interval (0, π).
Solution:

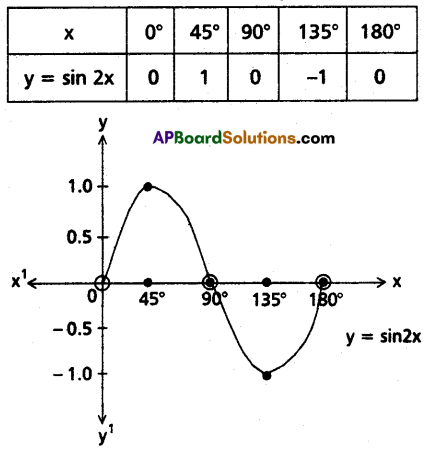
Question 9.
Evaluate \(\cos ^2 52 \frac{1}{2}^{\circ}-\sin ^2 22 \frac{1}{2}^{\circ}\).
Solution:

Question 10.
If sinh x = 3, then show that x = log_e(3 + √10).
Solution:
Given sinh x = 3
⇒ x = sinh^-1(3)
= log_e(3 + \(\sqrt{3^2+1}\))
= log_e(3 + \(\sqrt{10}\))

Section – B
(5 × 4 = 20 Marks)

II. Short Answer Type Questions.

• Attempt Any Five questions.
• Each question carries Four marks.

Question 11.
If A = \(\left[\begin{array}{lll}
a_1 & b_1 & c_1 \\
a_2 & b_2 & c_2 \\
a_3 & b_3 & c_3
\end{array}\right]\) is the non-singular matrix, then A is invertible and proves that \(A^{-1}=\frac{{Adj} A}{{det} A}\).
Solution:

Question 12.
If \(\bar{a}, \bar{b}, \bar{c}\) are non-coplanar vectors, prove that the following four points are co-planar \(6 \bar{a}+2 \bar{b}-\bar{c}, 2 \bar{a}-\bar{b}+3 \bar{c},-\bar{a}+2 \bar{b}-4 \bar{c}\), \(-12 \bar{a}-\bar{b}-3 \bar{c}\).
Solution:

Question 13.
If \(\bar{a}+\bar{b}+\bar{c}\) = 0, |\(\bar{a}\)| = 3, |\(\bar{b}\)| = 5 and |\(\bar{c}\)| = 7, then find the angle between \(\bar{a}\) and \(\bar{b}\).
Solution:

Question 14.
If a, b, c are non-zero real numbers and α, β are solutions of the equation a cos θ + b sin θ = c, then show that:
(i) sin α + sin β = \(\frac{2 b c}{a^2+b^2}\)
(ii) sin α . sin β = \(\frac{c^2-a^2}{a^2+b^2}\)
Solution:
Given a cos θ + b sin θ = c
⇒ a cos θ = c – b sin θ
⇒ a² cos²θ = (c – b sin θ)²
⇒ a² (1 – sin²θ) = c² + b² sin²θ – 2bc sin θ
⇒ a² – a² sin²θ = c² + b² sin²θ – 2bc sin θ
⇒ (a² + b²) sin²θ – 2bc sin C + (c² – a²) = 0 ………(1)
since α and β are solutions of the given equation.
∴ sin α, sin β are the roots of (1)
(i) sum of the roots = sin α + sin β
= \(\frac{-(-2 b c)}{a^2+b^2}\)
= \(\frac{2 b c}{a^2+b^2}\)
(ii) product of the roots = sin α . sin β = \(\frac{c^2-a^2}{a^2+b^2}\)

Question 15.
Solve the equation cot²x – (√3 + 1) cot x + √3 = 0; 0 < x < \(\frac{\pi}{2}\).
Solution:
Given cot²x -(√3 + 1) cot x + √3 = 0
⇒ cot²x – √3 cot x – cot x + √3 = 0
⇒ cot x (cot x – √3) – 1(cot x – √3) = 0
⇒ (cot x – 1) (cot x – √3) = 0
∴ cot x – 1 = 0
⇒ cot x = 1
⇒ tan x = 1
⇒ x = nπ + \(\frac{\pi}{4}\), n ∈ z
∴ cot x – √3 = 0
⇒ cot x = √3
⇒ tan x = \(\frac{1}{\sqrt{3}}\)
⇒ x = nπ + \(\frac{\pi}{6}\), n ∈ z
0 < x < \(\frac{\pi}{2}\)
∴ x = \(\frac{\pi}{6}\), \(\frac{\pi}{4}\)

Question 16.
Prove that \(\tan ^{-1} \frac{1}{7}+\tan ^{-1} \frac{1}{13}-\tan ^{-1} \frac{2}{9}\) = 0.
Solution:

Question 17.
Prove that \(\frac{1+\cos (A-B) \cos C}{1+\cos (A-C) \cos B}=\frac{a^2+b^2}{a^2+c^2}\)
Solution:
L.H.S = \(\frac{1+\cos (A-B) \cos C}{1+\cos (A-C) \cos B}\)

Section – C
(5 × 7 = 35 Marks)

III. Long Answer Type Questions.

• Attempt Any Five questions.
• Each question carries Seven marks.

Question 18.
Let f: A → B, g: B → C be bijections, then prove that (gof)^-1 = f^-1 o g^-1.
Solution:
f: A → B, g: B → C are bijections
⇒ gof: A → C is a bijection
Also g^-1: C → B and f^-1: B → A are bijections
⇒ f^-1 o g^-1: C → A is a bijection.
Let c be any element of C.
Then ∃ an element b ∈ B such that g(b) = c
⇒ b = g^-1(c)
Also ∃ an element a ∈ A such that f(a) = b
⇒ a = f^-1(b)
Now (gof) (a) = g(f(a) = g(b) = c
⇒ a = (g o f)^-1 (c)
⇒ (g o f)^-1 (c) = a
Also (f^-1 o g^-1) (c) = f^-1(g^-1(c))
= f^-1(b)
= a
From (1) and (2);
(g o f)^-1(c) = f^-1 o g^-1(c)
⇒ (g o f)^-1 = f^-1 o g^-1

Question 19.
Using mathematical induction, prove that:
\(\left(1+\frac{3}{1}\right)\left(1+\frac{5}{4}\right)\left(1+\frac{7}{9}\right) \ldots\left(1+\frac{2 n+1}{n^2}\right)=(n+1)^2\)
Solution:
Let p(n) be the statement.
\(\left(1+\frac{3}{1}\right)\left(1+\frac{5}{4}\right)\left(1+\frac{7}{9}\right) \ldots\left(1+\frac{2 n+1}{n^2}\right)=(n+1)^2\)
and let S(n) be the product on the LHS
since S(1) = 1 + 3 = 4 = (1 + 1)² = 4
∴ P(a) 4 time for n = 1
Assume that p(n) is true for n = K
S(K) = \(\left(1+\frac{3}{1}\right)\left(1+\frac{5}{4}\right)\left(1+\frac{7}{9}\right) \ldots\left(1+\frac{2 k+1}{k^2}\right)=(k+1)^2\)
We show that P(n) is true for n = K + 1
\(\left(1+\frac{3}{1}\right)\left(1+\frac{5}{4}\right)\left(1+\frac{7}{9}\right) \cdots\left(\frac{k^2+2 K+1}{K^2}\right)\left(1+\frac{2 k+2+1}{(K+1)^2}\right)\)
= (k + 1)² + 2k + 3
= k² + 2k + 1 + 2k + 3
= k² + 4k + 4
= (k + 2)²
= (k + 1 + 1)²
∴ P(n) is true for n = k + 1
By the principle of Mathematical Induction p(n) is true & n ∈ N

Question 20.
Find the value of x if \(\left|\begin{array}{ccc}
x-2 & 2 x-3 & 3 x-4 \\
x-4 & 2 x-9 & 3 x-16 \\
x-8 & 2 x-27 & 3 x-64
\end{array}\right|\) = 0
Solution:

⇒ (x – 2) (30 – 24) – (2x – 3) (10 – 6) + (3x – 4)(4 – 3) = 0
⇒ (x – 2) (6) – (2x – 3) (4) + (3x – 4) (1) = 0
⇒ 6x – 12 – 8x + 12 + 3x – 4 = 0
⇒ x – 4 = 0
⇒ x = 4

Question 21.
Examine whether the equations are consistent or inconsistent and if consistent find the complete solution:
x + y + z = 6, x – y + z = 2, 2x – y + 3z = 9
Solution:
Given system of equations are
x + y + z = 6
x – y + z = 2
2x – y + 3z = 9
Given the system of equations can be represented as a matrix equation AX = B


Here r₁ = 3, r₂ = 3 and n = 3
∴ r₁ = r₂ = n
∴ The given system of equations is consistent and it has unique solution.
∴ Given equations are equivalent to
x + y + z = 6 ………(1)
y = 2
z = 3
From (1), x + 2 + 3 = 6
⇒ x = 1
∴ x = 1, y = 2, z = 3

Question 22.
\(\bar{a}, \bar{b}, \bar{c}\) are three vectors, then prove that \((\bar{a} \times \bar{b}) \times \bar{c}=(\bar{a} \cdot \bar{c}) \bar{b}-(\bar{b} \cdot \bar{c}) \bar{a}\).
Solution:
Equation (1) is evidently true if a and b are parallel.
Now suppose that a and b are non-parallel.
Let O denote the origin. Choose points A and B such that \(\overline{\mathrm{OA}}=\overline{\mathrm{a}}\) and \(\overline{\mathrm{OB}}=\overline{\mathrm{b}}\)
Since \(\bar{a}\) and \(\bar{b}\) are non-parallel, the points O, A, and B are non-collinear. Hence they determine a plane.
Let i denote the unit vector along \(\bar{OA}\).
Let j be a unit vector in the OAB plane perpendicular to i.

Question 23.
If A, B, C are angles in a triangle, then prove that: sin²A + sin²B – sin²C = 2 sin A sin B cos C.
Solution:
Since A, B, C are angles in a triangle.
∴ A + B + C = 180°
L.H.S = sin²A + sin²B – sin²C
= sin²A + sin (B + C) sin (B – C)
= sin²A + sin(180 – A) sin (B – C)
= sin²A + sin A sin (B – C)
= sin A [sin A + sin (B – C)]
= sin A [sin(180 – (B + C)) + sin(B – C)]
= sin A [sin (B + C) + sin (B – C)]
= sin A [2 sin B cos C]
= 2 sin A sin B cos C
= R.H.S.
∴ sin²A + sin²B – sin²C = 2 sin A sin B cos C

Question 24.
In ΔABC, show that: (r₁ + r₂) \(\sec ^2 \frac{C}{2}\) = (r₂ + r₃) \(\sec ^2 \frac{A}{2}\) = (r₃ + r₁) \(\sec ^2 \frac{B}{2}\).
Solution: