AP State Syllabus AP Board 9th Class Maths Solutions Chapter 10 Surface Areas and Volumes Ex 10.4 Textbook Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 10th Lesson Surface Areas and Volumes Exercise 10.4
![]()
Question 1.
The radius of a sphere is 3.5 cm. Find its surface area and volume.
Solution:
Radius of the sphere, r = 3.5 cm

![]()
Question 2.
The surface area of a sphere is 1018\(\frac{2}{7}\) cm2 . What is its volume ?
Solution:
Surface area of sphere = 4πr2
= 1018\(\frac{2}{7}\) cm2
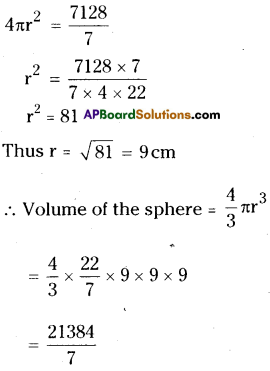
= 3054.857cm3
≅ 3054.86cm3
Question 3.
The length of equator of the globe is 44 cm. Find its surface area.
Solution:
Length of the equator of the globe 2πr = 44 cm.
2 × \(\frac{22}{7}\) × r = 44
∴ r = \(\frac{44 \times 7}{2 \times 22}\) = 7cm
∴ surface area = 4πr2
= 4 × \(\frac{22}{7}\) × 7 × 7
= 4 × 22 × 7
= 616cm2
![]()
Question 4.
The diameter of a spherical ball is 21 cm. How much leather is required to prepare 5 such balls?
Solution:
Diameter of the spherical ball d’ = 21 cm
Thus, its radius r = \(\frac{d}{2}=\frac{21}{2}\) = 10.5 cm
Surface area of one ball = 4πr2
= 4 × \(\frac{22}{7}\) × 10.5 × 10.5
= 88 × 1.5 × 10.5 = 1386 cm2
∴ Leather required for 5 such balls
= 5 × 1386 = 6930 cm2
Question 5.
The ratio of radii of two spheres is 2 : 3. Find the ratio of their surface areas and volumes.
Solution:
Ratio of radii r1 : r2 = 2 : 3
Ratio of surface area
= 4πr12 : 4πr22
= 22: 32 = 4 : 9
Ratio of volumes
= 4/3 πr13 : 4/3 πr23
= 23 : 33 = 8 : 27
Question 6.
Find the total surface area of hemisphere of radius 10 cm. (Use π = 3.14)
Solution:
Radius of the hemisphere = 10 cm
Total surface area of the hemisphere = 3πr2
= 3 × 3.14 × 10 × 10
= 9.42 × 100
= 942 cm2
![]()
Question 7.
The diameter of a spherical balloon increases from 14 cm. to 28 cm. as air is being pumped into it. Find the ratio of surface areas of the balloons in the
two cases.
Solution:
The diameter of the balloon, d = 14 cm
Thus, its radius, r = \(\frac{d}{2}=\frac{14}{2}\) = 7 cm
∴ Surface area = 4πr2 = 4 × \(\frac{22}{7}\) × 7 × 7
= 88 × 7 = 616cm2
When air is pumped, the diameter = 28 cm
thus its radius = \(\frac{d}{2}=\frac{28}{2}\) = 14 cm
Its surface area = 4πr2
= 4 × \(\frac{22}{7}\) × 14 × 14
= 88 × 28 = 2464 cm2
Ratio of areas = 616 : 2464
= 1 : 4
(OR)
Original radius = \(\frac{14}{2}\) = 7 cm
Increased radius = \(\frac{28}{2}\) = 14cm
Ratio of areas = r12 : r22
= 72 : 142
= 7 × 7 : 14 × 14
= 1:4
![]()
Question 8.
A hemispherical bowl is made of brass, 0.25 cm thickness. The inner radius of the bowl is 5 cm. Find the ratio of outer surface area to inner surface area.
Solution:
Inner radius of the hemisphere ‘r’ = 5 cm
Outer radius of the hemisphere ‘R’
= inner radius + thickness
= (5 + 0.25) cm = 5.25 cm
Ratio of areas = 3πR2: 3πr2
= R2 : r2
= (5.25)2: 52
= 27.5625 : 25
= 1.1025:1
= 11025 : 10000
= 441 : 400
[Note : If we read “radius as diameter” then we get the T.B. answer]
Question 9.
The diameter of a lead ball is 2.1 cm. The density of the lead used is 11.34 g/c3. What is the, weight of the ball ?
Solution:
The diameter of the ball = 2.1 cm
Thus, its radius, r = \(\frac{d}{2}=\frac{2.1}{2}\) = 1.05 cm
Volume of the ball V’ = \(\frac{4}{3}\)πr3
= \(\frac{4}{3} \times \frac{22}{7}\) x 1.053 = \(\frac{101.87}{21}\)
∴Weight of the ball = Volume × density
= 4.851 × 1.34
= 55.010
![]()
Question 10.
A metallic cylinder of diameter 5 cm 1 and height 3 \(\frac{1}{3}\) cm is melted and cast into a sphere. What is its diameter ?
Solution:
Diameter of the cylinder’d’ = 5 cm
Thus, its radius, r = \(\frac{d}{2}=\frac{5}{2}\) = 2.5 cm
Height of the cylinder,
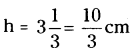
Volume of the cylinder
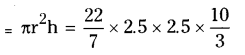
Given that cylinder melted to form sphere
∴ Volume of the sphere = Volume of the cylinder
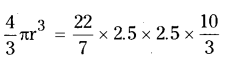
(Where r is the radius of the sphere)
r3 = \(\frac{3}{4}\) × 2.5 × 2.5 × \(\frac{10}{3}\)
r3 = 2.53
∴ r = 2.5 cm
Hence its diameter, d = 2r
= 2 × 2.5 = 5 cm
![]()
Question 11.
How many litres of milk can a hemispherical bowl of diameter 10.5 cm hold ?
Solution:
Diameter of the hemispherical bowl = 10.5 cm
Thus its radius = \(\frac{d}{2}=\frac{10.5}{2}\) = 5.25cm
Quantity of milk, the bowl can hold = Volume of the bowl = \(\frac{2}{3}\)πr3
= \(\frac{2}{3} \times \frac{22}{7}\) × 5.25 × 5.25 × 5.25
= 303.1875 cm3
= \(\frac{303.1875}{1000}\) lit = 0.303 lit.
Question 12.
A hemispherical bowl has diameter 9 cm. The liquid is poured into cylindrical bottles of diameter 3 cm and height 3 cm. If a full bowl of liquid is Riled in the bottles, find how many
bottles are required ?
Solution:
Diameter of the hemispherical bowl ‘d’ = 9 cm
Its radius, r = \(\frac{d}{2}=\frac{9}{2}\) = 4.5cm
Volume of its liquid = Volume of the bowl = \(\frac{2}{3}\) πr3
= \(\frac{2}{3} \times \frac{22}{7}\) × 4.5 × 45 × 4.5
Diameter of the cylindrical bottle, d = 3 cm
Its radius, r = \(\frac{d}{2}\)
= \(\frac{3.0}{2}\)
= 1.5cm
Height of the bottle, h = 3 cm
Let the number of bottles required = n
Then total volumes of these n bottles = n πr2h
But this is equal to volume of the bowl
Hence n. \(\frac{22}{7}\) × 1.5 × 1.5 × 3
= \(\frac{2}{3} \times \frac{22}{7}\) × 4.5 × 4.5 × 4.5
∴ n = \(\frac{2}{3} \times \frac{20.25}{1.5}\) = 9
∴ Number of bottles required = 9
