SCERT AP 10th Class Maths Textbook Solutions Chapter 5 వర్గ సమీకరణాలు Exercise 5.2 Textbook Exercise Questions and Answers.
AP State Syllabus 10th Class Maths Solutions 5th Lesson వర్గ సమీకరణాలు Exercise 5.2
ప్రశ్న 1.
కారణాంక పద్ధతిన క్రింది వర్గ సమీకరణాల మూలాలను కనుగొనుము.
(i) x2 – 3x – 10 = 0
సాధన.
x2 – 3x – 10 = 0
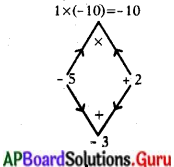
x2 – 5x + 2x – 10 = 0
x (x – 5) + 2(x – 5) = 0
(x – 5) (x + 2) = 0
x – 5 = 0
x = 5
x + 2 = 0
x = – 2.
∴ మూలాలు 5 మరియు – 2.
![]()
(ii) 2x22 + x – 6 = 0
సాధన.
2x2 + x – 6 = 0
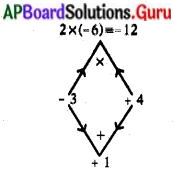
2x2 – 3x + 4x – 6 = 0
x (2x – 3) + 2(2x – 3) = 0
(2x – 3) (x + 2) = 0
2x – 3 = 0
2x = 3
x + 2 = 0
x = – 2
∴ మూలాలు , మరియు – 2.
(iii) √2x2 + 7x + 5√2 = 0
సాధన.
√2 x2 + 7x + 5√2 = 0
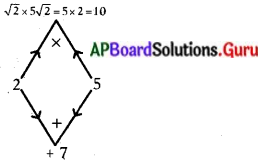
√2 x2 + 5x + 2x + 5√2 = 0
x(√2 x + 5) + √2 (√2 x + 5) = 0
(√2 x + 5) (x + √2) = 0
√2x + 5 = 0
√2x = – 5
x = \(\frac{-5}{\sqrt{2}}\)
x + √2 = 0
x = – √2
∴ మూలాలు \(\frac{-5}{\sqrt{2}}\), మరియు – √2.
![]()
(iv) 2x2 – x + \(\frac{1}{8}\) = 0
సాధన.
2x2 – x + \(\frac{1}{8}\) = 0
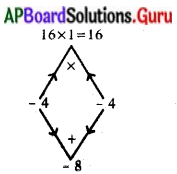
\(\frac{16 x^{2}-8 x+1}{8}\) = 0
∴ 16x2 – 4x + 4x + 1 = 0
4x(4x – 1) – 1(4x – 1) = 0.
(4x – 1)(4x – 1) = 0
4x – 1 = 0
4x = 1
x = \(\frac{1}{4}\)
4x – 1 = 0
4x = 1
x = \(\frac{1}{4}\)
∴ మూలాలు \(\frac{1}{4}\), మరియు \(\frac{1}{4}\)
(v) 100x2 – 20x + 1 = 0
సాధన.
100x2 – 20x + 1 = 0
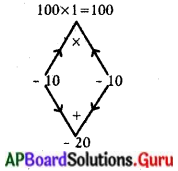
100x2 – 10x – 10x + 1 = 0
10x(10x – 1) – 1(10x – 1) = 0
(10x – 1) (10x – 1) = 0
(10x – 1)2 = 0
10x – 1 = 0
10x = 1
x = \(\frac{1}{10}\) ఈ సందర్భంలో మూలాలు సమానం.
∴ మూలాలు \(\frac{1}{10}\), \(\frac{1}{10}\).
![]()
(vi) x(x + 4) = 12
సాధన.
x(x + 4) = 12
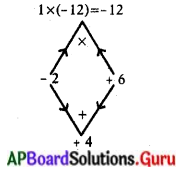
x2 + 4x = 12
x2 + 4x – 12 = 0
x2 – 2x + 6x – 12 = 0
x(x – 2) + 6(x – 2) = 0
(x – 2) (x + 6) = 0
x – 2 = 0
x = 2
x + 6 = 0
x = – 6
∴ మూలాలు 2 మరియు – 6.
(vii) 3x2 – 5x + 2 = 0
సాధన.
3×2 – 5x + 2 = 0
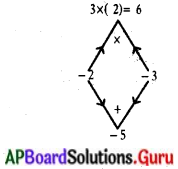
3x2 – 2x – 3x + 2 = 0
x (3x – 2) – 1(3x – 2) = 0
(3x – 2) (x – 1) = 0
3x – 2 = 0
3x = 2
x = \(\frac{2}{3}\)
x – 1 = 0
x = 1
∴ మూలాలు \(\frac{2}{3}\), మరియు 1.
![]()
(viii) x – \(\frac{3}{x}\) = 2
సాధన.
x – \(\frac{3}{x}\) = 2
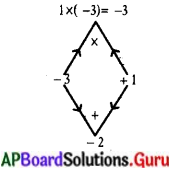
\(\frac{x^{2}-3}{x}\) = 2
x2 – 3 = 2x
x2 – 2x – 3 = 0
x2 – 3x + x – 3 = 0 –
x (x – 3) + 1(5 – 3) = 0.
(x – 3) (x + 1) = 0
x – 3 = 0
x = 3
x + 1 = 0
x = – 1
∴ మూలాలు 3 మరియు – 1.
(ix) 3(x – 4)2 – 5(x – 4) = 12
సాధన.
3(x – 4)2 – 5(x – 4) = 12
x – 4 = t అనుకొంటే
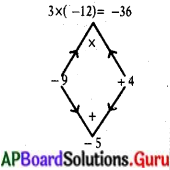
3t2 – 5t = 12.
3t2 – 5t – 12 = 0
3t2 – 9t + 4t – 12 = 0.
3t (t – 3) + 4(t – 3) = 0
(t – 3) (3t + 4) = 0
t – 3 = 0
t = 3
3t + 4 = 0
3 t = – 4
3 t = \(\frac{-4}{3}\)
కాని x – 4 = t
x – 4 = 3
x = 3 + 4 = 7
x – 4 = \(\frac{-4}{3}\)
x = \(\frac{-4}{3}\) + 4
x = \(\frac{-4+12}{3}\)
x = \(\frac{8}{3}\)
∴ మూలాలు 7 మరియు \(\frac{8}{3}\).
![]()
ప్రశ్న 2.
మొత్తము 27, లబ్ధము 182 అయ్యే విధంగా రెండు సంఖ్యలను – కనుగొనుము.
సాధన.
ఒక సంఖ్య = x అనుకొందాం.
రెండవ సంఖ్య = 27 – x
(∵ రెండు సంఖ్యల మొత్తం 27)
లెక్క ప్రకారం రెండు సంఖ్యల లబ్దం = 182
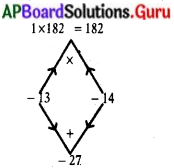
x(27 – x) = 182
27x – x2 = 182
– x2 + 27x – 182 = 0
x2 – 27x + 182 = 0
x2 – 13x – 14x + 182 = 0
x(x – 13) – 14(x – 13) = 0
(x – 13) (x – 14) = 0
x – 13 = 0
x = 13
x – 14 = 0
x = 14
ఒక సంఖ్య x = 13 అయిన రెండవ సంఖ్య = 27 – x = 27 – 13 = 14
ఒక సంఖ్య x = 14 అయిన రెండవ సంఖ్య = 27 – x = 27 – 14 = 13
∴ కావలసిన సంఖ్యలు 13, 14
సరిచూసుకోవడం :
13 × 14 = 182
![]()
ప్రశ్న 3.
రెండు వరుస ధన పూర్ణ సంఖ్యల వర్గాల మొత్తము 613 అయిన ఆ సంఖ్యలను కనుగొనుము.
సాధన.
మొదటి సంఖ్య = x అనుకొందాం.
రెండవ సంఖ్య = x + 1
(∵ రెండు సంఖ్యలు వరుస ధనపూర్ణ సంఖ్యలు)
రెండు వరుస ధనపూర్ణ సంఖ్యల వర్గాల మొత్తం = 613
x2 + (x + 1)2 = 613
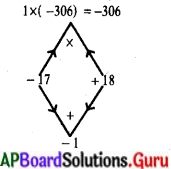
x2 + x2 + 2x + 1 = 613
2x2 +2x + 1 – 613 = 0
2x2 + 2x – 612 = 0
2(x2 + x – 306) = 0
x2 + x – 306 = 0
x2 – 17x + 18x – 306 = 0
x(x – 17) + 18(x – 17) = 0
(x – 17) (x + 18) = 0
x – 17 = 0
x = 17
x + 18 = 0
x = – 18
∴ x = – 18 ధనపూర్ణ సంఖ్య కాదు.
∴ x = 17 ధనపూర్ణ సంఖ్య
మొదటి సంఖ్య x = 17 .
రెండవ సంఖ్య = x + 1 = 17 + 1 = 18
సరిచూసుకోవడం :
172 + 182 = 289 + 324 = 613.
![]()
ప్రశ్న 4.
ఒక లంబకోణ త్రిభుజం యొక్క ఎత్తు దాని భూమి కంటే 7 సెం.మీ. తక్కువ. కర్ణము పొడవు 13 సెం.మీ. అయిన మిగిలిన రెండు భుజాలను కనుగొనుము.
సాధన.
ఒక లంబకోణ త్రిభుజం యొక్క భూమి = x సెం.మీ. . అనుకొనుము.
ఎత్తు = (x – 7) సెం.మీ.
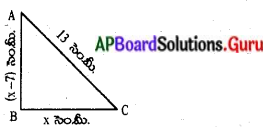
పైథాగరస్ సిద్ధాంతం ప్రకారం భుజము 2 + భుజము 2 = కర్ణము?
x2 + (x – 7)2 = 132
x2 + x2 – 14x + 49 = 169
2x2 – 14x + 49 – 169 = 0
2x2 – 14x – 120 = 0
2(x2 – 7x – 60) = 0
x2 – 7x – 60 = 0
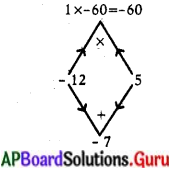
x2 – 12x + 5x – 60 = 0
(x – 12) + 5(x – 12) = 0
(x – 12) (x + 5) = 0
x – 12 = 0
x = 12
x + 5 = 0
x = – 5 త్రిభుజ భుజం కొలత రుణాత్మకం కాదు.
కావున x = 12 భూమి = 12 సెం.మీ.
ఎత్తు = x – 7 = 12 – 7 = 5 సెం.మీ.
సరిచూచుట :
భూమి 2 + ఎత్తు = 122 + 52
= 144 + 25 = 169
= (13)2 = కర్ణం2.
![]()
ప్రశ్న 5.
ఒక కుటీర పరిశ్రమలో ప్రతిరోజు ఒక నియమిత సంఖ్యలో వస్తువులను తయారు చేస్తారు. ఒక రోజు తయారైన ఒక్కొక్క వస్తువు ఖరీదు (రూపాయిలలో) ఆ రోజు తయారైన వస్తువుల సంఖ్యకు రెట్టింపు కంటే -3 ఎక్కువ. ఆ రోజు తయారైన మొత్తం వస్తువుల ఖరీదు ₹ 90 అయిన ఆ రోజు తయారైన మొత్తం వస్తువుల సంఖ్య మరియు ఒక్కొక్క వస్తువు ఖరీదును కనుగొనుము.
సాధన.
ఒక రోజు తయారైన వస్తువుల సంఖ్య = x అనుకొందాం.
ఆ రోజు తయారైన ఒక్కొక్క వస్తువు ఖరీదు = 2x + 3
(∵ ఆ రోజు తయారైన వస్తువుల సంఖ్యకు రెట్టింపు కంటే 3 ఎక్కువ).
ఆ రోజు తయారైన మొత్తం వస్తువుల ఖరీదు = ₹ 90
x(2x + 3) = 90
2x2 + 3x = 90
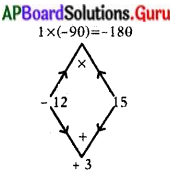
2x2 + 3x – 90 = 0.
2x2 – 12x + 15x – 90 = 0
2x (x – 6) + 15 (x – 6) = 0
(x – 6) (2x + 15) = 0
2x + 15 = 0
2x = – 15
x = \(\frac{-15}{2}\)
x – 6 = 0
x = 6
వస్తువుల సంఖ్య రుణాత్మకం కాదు.
కావున ఒక రోజు తయారైన వస్తువుల సంఖ్య = 6
ఆ రోజు తయారైన ఒక్కొక్క వస్తువు ఖరీదు = 2 × (6) + 3 = 12 + 3 = ₹ 15
సరిచూచుకోవడం :
మొత్తం ఖరీదు 6 × 15 = 90
![]()
ప్రశ్న 6.
ఒక దీర్ఘచతురస్రము యొక్క చుట్టుకొలత 28 మీ. మరియు దాని వైశాల్యం 40 చ.మీ. అయిన దీర్ఘచతురస్రము యొక్క కొలతలను కనుగొనుము.
సాధన.
దీర్ఘచతురస్ర పొడవు = x మీ.
దీర్ఘచతురస్ర వెడల్పు = y మీ. అనుకొనుము.

లెక్క ప్రకారం దీర్ఘచతురస్రం యొక్క చుట్టుకొలత = 28 మీ.
2 (x + y) = 28
⇒ x + y = \(\frac{28}{2}\) = 14
⇒ y = 14 – x …………. (1)
మరియు దీర్ఘచతురస్ర వైశాల్యం = 40 చ.మీ.
x . y = 40 ………… (2)
(1) & (2) ల నుండి
x (14 – x) = 40
14x – x2 = 40
– x2 + 14x – 40 = 0
x2 – 14x + 40 = 0
x2 – 10x – 4x + 40 = 0
x(x – 10) – 4(x – 10) = 0
(x – 10) (x – 4) = 0
x – 10 = 0
x = 10
x – 4 = 0
x = 4
పొడవు x = 10 మీ. అయితే ఈ వెడల్పు 14 – x = 14 -10 = 4 మీ.
పొడవు 4 మీ. అయితే వెడల్పు 14 – 4 = 10 మీ.
∴ దీర్ఘచతురస్ర కొలతలు 10 మరియు 4.
![]()
ప్రశ్న 7.
ఒక త్రిభుజము యొక్క భూమి, దాని ఎత్తు కంటే 4 సెం.మీ. ఎక్కువ. ఈ త్రిభుజ వైశాల్యము 48 చ.సెం.మీ. అయిన దాని భూమిని, ఎత్తును కనుగొనుము.
సాధన.
త్రిభుజము యొక్క ఎత్తు = x సెం.మీ. అనుకొనిన
భూమి = (x + 4) సెం.మీ.
లెక్క ప్రకారం త్రిభుజం యొక్క వైశాల్యము = 48 చ.సెం.మీ.
\(\frac{1}{2}\) × భూమి × ఎత్తు = 48
\(\frac{1}{2}\) × (x + 4) x = 48
\(\frac{1}{2}\) × (x2 + 4x) = 48
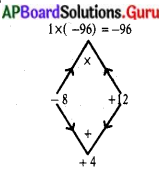
x2 + 4x = 96
x2 + 4x-96 = 0
x2 – 8x + 12x – 96 = 0
x(x – 8) + 12(x – 8) = 0
(x – 8) (x + 12) = 0
x – 8 = 0
x = 8
x + 12 = 0
x= – 12
త్రిభుజం యొక్క ఎత్తు రుణాత్మకం కాదు.
కావున x = 8.
∴ త్రిభుజం యొక్క ఎత్తు x = 8 సెం.మీ.
సరిచూచుకోవడం :
భూమి x + 4 = 8 + 4 = 12 సెం.మీ.
త్రిభుజ వైశాల్యం = \(\frac{1}{2}\) × 8 × 12 = 48 చ.సెం.మీ.
![]()
ప్రశ్న 8.
రెండు రైళ్లు ఒక స్టేషన్ నుంచి ఒకే సమయంలో ఒకటి పడమరకు, మరియొకటి ఉత్తరం వైపుకు బయలుదేరును. మొదటి రైలు, రెండవ రైలు కంటే 5 కి.మీ./గంట ఎక్కువ వేగంతో ప్రయాణిస్తుంది. అవి బయలుదేరిన రెండు గంటల తరువాత ఒకదానికొకటి 50 కి.మీ. దూరంలో వున్న ఒక్కొక్క రైలు సగటు వేగం ఎంత ?
సాధన.
రెండవ రైలు వేగం = x కి.మీ./గం. అనుకొనిన ,
మొదటి రైలు వేగం = (x + 5) కి.మీ/గం.
రెండు రైళ్ళు B వద్ద బయలుదేరాయి అనుకొంటే
దూరం = కాలం × వేగం
2 గంటలలో మొదటి రైలు ప్రయాణించిన దూరం BC = 2(x + 5) = 2x + 10
రెండవ రైలు ప్రయాణించిన దూరం BA = 2x
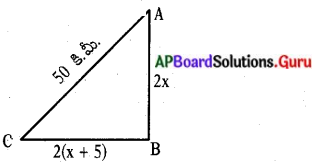
ABC లంబకోణ త్రిభుజము AB2 + BC2 = AC (∵ పైథాగరస్ సిద్ధాంతం ప్రకారం) ,
(2x)2 + (2x + 10)2 = 502
4x2 + (2x)2 + 2.2x. 10 + 102 = 2500
4x2 + 4x2 + 40x + 100 = 2500
8x2 + 40x + 100 – 2500 = 0
8x2 + 40x – 2400 = 0
8(x2 + 5x – 300) = 0
x2 + 5x – 300 = 0
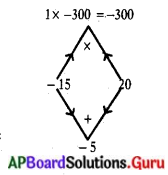
x2 – 15x + 20x – 300 = 0
x(x – 15) + 20(x – 15) = 0
(x – 15) (x + 20) = 0
x – 15 = 0
x = 15
x + 20 = 0
x = – 20
వేగము రుణాత్మకం కాదు. కావున x = 15.
∴ రెండవ రైలు వేగం x = 15 కి.మీ/గం.
మొదటి రైలు వేగం x + 5 = 15 + 5 = 20 కి.మీ/గం.
![]()
ప్రశ్న 9.
60 మంది విద్యార్థులు గల తరగతిలో ప్రతి అబ్బాయి, అమ్మాయిల సంఖ్యకు సమానమైన సొమ్మును, ప్రతి అమ్మాయి అబ్బాయిల సంఖ్యకు సమానమైన సొమ్మును చందాగా ఇచ్చారు. మొత్తం వసూలైన సొమ్ము ₹ 1600 అయిన తరగతిలో ఎంత మంది అబ్బాయిలు గలరు ?
సాధన.
తరగతిలోని అబ్బాయిల సంఖ్య = x
అనుకొనిన అమ్మాయిల సంఖ్య = 60 – x
(∵ తరగతిలో విద్యార్థులు 60 మంది)
తరగతిలోని ప్రతి అబ్బాయి చెల్లించే చందా = x (60 – x)
అబ్బాయిల చందా = x (60 – x) = 60x – x2
తరగతిలోని ప్రతి అమ్మాయి చెల్లించే చందా = x
అమ్మా యిల చందా = (60 – x)x = 60x – x2
మొత్తం వసూలైన సొమ్ము = ₹ 1600.
అబ్బాయిల చందా + అమ్మాయిల చందా= 1600.
60x – x2 + 60x – x2 = 1600
120x – 2x2 = 1600
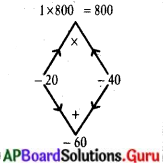
– 2x2 + 120x – 1600 = 0
– 2(x2 – 60x + 800) = 0
∴ x2 – 60x + 800 = 0
x2 – 20x – 40x + 800 = 0
x(x – 20) – 40 (x – 20) = 0
(x – 20) (x – 40) = 0
x – 20 = 0
x = 20.
x – 40 = 0
x = 40
తరగతిలోని అబ్బాయిల సంఖ్య x = 20 లేదా 40.
తరగతిలోని అమ్మాయిల సంఖ్య x = 40 లేదా 20.
![]()
ప్రశ్న 10.
గంటకు 3 కి.మీ వేగంతో ప్రయాణిస్తున్న ఒక నదిలో ఒక మోటారు బోటు 24 కి.మీ. దూరము ప్రయాణించి తిరిగి బయలుదేరిన స్థానానికి రావడానికి పట్టిన కాలం 6 గంటలైన బోటు స్థిరవేగంతో ప్రయాణించినదని భావించి దాని వేగమును కనుగొనుము.
సాధన.
నది ప్రవాహ వేగం = 3 కి.మీ./గం.
నిలకడ నీటిలో పడవ వేగం = x కి.మీ/గం. అనుకొనుము.
ప్రవాహ దిశలో పడవ వేగం = (x + 3) కి.మీ/గం||
24 కి.మీ ప్రయాణించుటకు పటుకాలం = దూరం/వేగం = 24/x + 3 గం.
ప్రవాహ దిశకు ఎదురుగా పడవ వేగం = (x – 3) కి.మీ/గం.
24 కి.మీ. ప్రయాణించుటకు పట్టు కాలం = \(\frac{24}{x-3}\) కి.మీ/గం.
మొత్తం ప్రయాణ కాలము = 6గం.
∴ \(\frac{24}{x+3}+\frac{24}{x-3}\) = 6
\(\frac{24(x-3)+24(x+3)}{(x+3)(x-3)}\) = 6
\(\frac{24 x-72+24 x+72}{x^{2}-9}\) = 6
\(\frac{48 x}{x^{2}-9}\) = 48x
6(x2 – 9) = 48x
6x2 – 54 = 48x
6x2 – 48x – 54 = 0
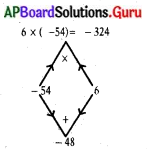
6x2 – 54x + 6x – 54 = 0
6x (x – 9) + 6(x – 9) = 0
(x – 9) (6x + 6) = 0
x – 9 = 0
6x + 6 = 0
6x = – 6
x = \(\frac{-6}{6}\)
x = – 1
పడవ వేగం రుణాత్మకం కాదు, కావున x = 9.
∴ నిలకడ నీటిలో పడవ వేగం x = 9 కి.మీ./గం.
సరిచూసుకోవడం :
ప్రవాహ దిశలో ప్రయాణ కాలం = \(\frac{24}{9+3}=\frac{24}{12}\) = 2 గం.
= \(\frac{24}{9-3}=\frac{24}{6}\) = 4 గం.
మొత్తం ప్రయాణ కాలం = 2 + 4 = 6 గం.
