Practice the AP 10th Class Maths Bits with Answers Chapter 6 Progressions on a regular basis so that you can attempt exams with utmost confidence.
AP State Syllabus 10th Class Maths Bits 6th Lesson Progressions with Answers
Question 1.
Which term of Answer:P., 18, 15, 12, ………….. equal to ‘0’ ?
Answer:
7
Explanation :
a = 18, d = 15 – 18 = -3
an = 0 ⇒ a + (n – 1)d = 0
18 + (n-1)(-3) = 0
(n-1)(-3) = -18
n – 1 = 6 ⇒ n = 7
![]()
Question 2.
Find the 21st term of an Answer:P., whose first two terms are – 3 and 4.
Answer:
137
Explanation :
a1 = -3, a2 = 4
⇒ d = 4 – (-3) = 7
a21 = a + 20d
= (-3) + 20(7)
= -3 + 140 = 137
Question 3.
Which term of G.P., 3, 3\(\sqrt{3}\) , 9,
equals to 243 ?
Answer:
9
Explanation :
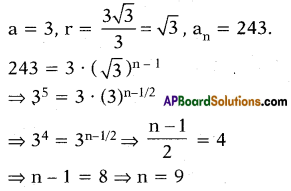
Question 4.
If a, b, c are in G.P., then find b’.
Answer:
\(\sqrt{\mathrm{ac}}\)
Question 5.
Find the sum of 10 terms of the progression log 2 + log 4 + log 8 + log 16 + ………………..
Answer:
55 log 2
![]()
Question 6.
Find nth term of a progression a, ar, ar2 ……………
Answer:
arn – 1
Question 7.
Find the sum of first 100 natural num-bers.
Answer:
5050
Question 8.
Find the common difference of Answer:P. log2 2, log2 4, log2 8.
Answer:
1
Explanation :
log22,log222 , log223
log22, 2 log22, 3 log22
1, 2, 3, ….
⇒ d = 1
Question 9.
In a GP, a1 = 20 and a4 = 540, then ‘ find ‘r’.
Answer:
3
Explanation :
a = 20, a4 = a – r3 = 540
⇒ 20.r3 = 540
⇒ r3 = \(\frac{540}{20}\) = 27 ⇒ r3 = 33 ⇒ r = 3
Question 10.
In an Answer:P., if a = 1, an = 20 and Sn = 399, then find ‘n’.
Answer:
38
Explanation :
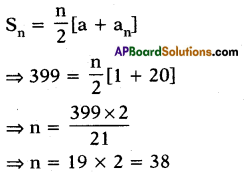
Question 11.
Find the common difference of the AP x – y, x, x + y.
Answer:
y
![]()
Question 12.
Find the common difference of the AP 1,-1, -3.
Answer:
– 2
Question 13.
If k, 2k + 1, 2k + 3 are three consecutive terms in Answer:P., then find the value of’k’.
Answer:
1
Explanation :
k + 1 – k = 2k + 3 – (2k + 1)
⇒ k + 1 = 2 ⇒ k = 1
Question 14.
Find the common difference in the AP 2a – b, 4a – 3b, 6a – 5b.
Answer:
2a – 2b.
Question 15.
Which term of the arithmetic progres-sion 24,21,18, is the first negative term ?
Answer:
10th term
Explanation :
a = 24, d = 21-24 = -3
an = a + (n – 1)d = 0
⇒ 24 + (n- 1) (-3) = 0
⇒ 24 – 3n + 3 = 0
⇒ 27 – 3n = 0
⇒ n = 9
∴ First negative term is ’10’.
Question 16.
Find the next term in Answer:P. \(\sqrt{3}, \sqrt{12}, \sqrt{27}\)
Answer:
\(\sqrt{48}\)
Question 17.
Find the common difference of an arithmetic progression in which
a25 – a12 = -52
Answer:
-4
Explanation :
a + 24d – (a + 11d) = – 52
an + 24d – a – 11d = – 52
⇒ 13d = – 52 ⇒ d = \(-\frac{52}{13}\) = – 4.
Question 18.
Find the sum of first ‘n’ odd natural numbers.
Answer:
n2
Question 19.
Find the common difference of an Answer:P. for which a18 – a14 = 32.
Answer:
8
Question 20.
Write a formula for sum of first ‘n’ terms in an AP.
Answer:
Sn = \(\frac{n}{2}\) [2a + (n – 1 )d] (or)
Sn = \(\frac{n}{2}\)[a + l]
Question 21.
Which term of the G.P. \(\frac{1}{3}, \frac{1}{9}, \frac{1}{27}, \ldots \ldots\) is \(\frac{1}{2187}\) ?
Answer:
7th
![]()
Question 22.
If an = \(\frac{\mathbf{n}}{\mathbf{n}+\mathbf{1}}\) then find a2017
Answer:
\(\frac{2017}{2018}\)
Question 23.
In an arithmetic progression, 4th term is 11 and 7th term is 17, then find its common difference.
Answer:
2
Explanation :
a4 = a + 3d = 11 and a7 = a + 6d = 17
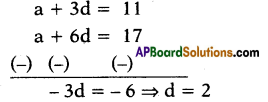
Question 24.
If x, x + 2, x + 6 are three consecutive terms in G.P. Find the value of’x’.
Answer:
2
Question 25.
The ’nth’ term of an Answer:P. is an = 3 + 2n, then find the common difference.
Answer:
2
Question 26.
If an = \(\frac{n(n+3)}{n+2}\)then find a17.
Answer:
\(\frac{340}{19}\)
Question 27.
In an AP an = \(\frac{5 n-3}{4}\), then find a7.
Answer:
8
Explanation :
a7 = \(\frac{5 \times 7-3}{4}=\frac{32}{4}\) = 8
![]()
Question 28.
Find the common difference of an arithmetic progression, whose 3rd term is 5 and 7th</sup? term is 9.
Answer:
1
Question 29.
If 4, a, 9 are in G.P., then find ‘a’,
Answer:
±6
Question 30.
If \(-\frac{2}{7}\) x , \(-\frac{7}{2}\) are in Geometric Progression, then find the value of x.
Answer:
1
Question 31.
If (i) – 1.0, – 1.5, – 2.0, – 2.5,…… and
(ii)- 1,-3, -9, -27, ………
ate two progressions, then which of them is a geometric progression ?
A) (i) only
B) (ii) only
C) (i) and (ii) both
D) None of them
Answer:
B) (ii) only
Question 32.
In a G.P., a = 81, r = \(-\frac{1}{3}\), then find a3.
Answer:
9
Explanation :
a3 = Answer:r2 = 81. (\(\left(\frac{-1}{3}\right)^{2}\)) ⇒ a3 = 9
Question 33.
Write a G.P. with r = 2 and a = 7.
Answer:
7, 14, 28 ………………..
Question 34.
If a, b, c are in AP, then find ’b’.
Answer:
\(\frac{a+c}{2}\) = b.
Question 35.
3, \(\frac{3}{2}\) , \(\frac{3}{4}\), …………. then find ‘r’.
Answer:
r = \(\frac{t_{2}}{t_{1}}=\frac{\frac{3}{2}}{3}=\frac{3}{2} \times \frac{1}{3}=\frac{1}{2}\)
Question 36.
Find the sum of first 1000 positive integers.
Answer:
500500
Question 37.
In the AP – 9, – 14, – 19, – 24, …………….. then find the value of a30 – a20.
Answer:
-50
Explanation :
a = – 9, d = -14 + 9 = -5
a30 = a + 29d
= – 9 + 29 (- 5)
= -9-145 = -154
a20 = a + 19d
= -9 + 19 (-5)
= -9-95 = -104
∴ a30 – a20 = – 154 + 104 = – 50
Question 38.
If 4, x, 9 are in G.P., then find ‘x’.
Answer:
6
![]()
Question 39.
Find 15th term of the AP x – 7, x – 2, x + 3, …………………….
Answer:
x + 63
Question 40.
\(\frac{1}{3}, \frac{1}{9}, \frac{1}{27}, \ldots\) find a7.
Answer:
\(\frac{1}{2187}\)
Question 41.
Write a formula 12 + 22 + 32 + … + n2.
Answer:
Σn2 = \(\frac{n(n+1)(2 n+1)}{6}\)
Question 42.
1 + \(\frac{1}{2}+\frac{1}{2^{2}}\) + ………….. then find ‘r’.
Answer:
\(\frac { 1 }{ 2 }\)
Question 43.
Find the common ratio of the G.P. 2, \(\sqrt{8}\), 4.
Answer:
\(\sqrt{2}\)
Question 44.
1,4,7,10, ……………… find ‘d’.
Answer:
3
Question 45.
If an = \(\frac{\mathbf{n}}{\mathbf{n}+\mathbf{2}}\), then find a3.
Answer:
\(\frac{3}{5}\)
![]()
Question 46.
Write an in G.P.
Answer:
arn-1 = an
Question 47.
2, \(\frac{5}{2}\), 3, find S25.
Answer:
S25 = 200
Explanation :
a = 2, d = \(\frac{5}{2}\) – 2 = \(\frac{1}{2}\)
S25 = \(\frac{n}{2}\)[2a + (n- 1) d]
= \(\frac{25}{2}\) [2(2) + 24 (1/2)]
= \(\frac{25}{2}\)[4 + 12]
= \(\frac{25}{2}\) x 16 = 25 x 8 = 200
Question 48.
Write G.M of a and b.
Answer:
\(\sqrt{\mathrm{ab}}\) = G.M.
Question 49.
In an Answer:P. a1 = -4, a6 = 6, then find a2
Answer:
-2.
Question 50.
If a, b, c are in Answer:P., then find ‘b’.
Answer:
\(\frac{a+c}{2}\) = b.
Question 51.
Which term of the G.P. 2, 6, 18, 54,…. is 2 x 310 ?
Answer:
11th term
Explanation :
a = 2, r = 3, an = 2 x 310
Answer:rn-1 = 2x 310
2 x 3n-1 = 2 x 310
⇒ n – 1 = 10 ⇒ n = 11
Question 52.
Find the sum of 15 terms of the Answer:P. 4, 7, 10, ………………
Answer:
375
Question 53.
Which term of the Answer:P. 100, 90, 80, …………… is zero ?
Answer:
11th term
Explanation :
a = 100, d = 90 – 100 = -10
an = a + (n – 1)d = 0
⇒ 100 + (n- 1)(- 10) = 0
⇒ (n – 1) (- 10) = – 100
⇒ n- 1 = 10
⇒ n = 11
Question 54.
Is the numbers, – 15, -11,-7, – 3, are in Answer:P. ? If so, find’d’.
Answer:
Yes, it is in Answer:P., with d = 4.
![]()
Question 55.
\(\frac{1}{\sqrt{2}},-2, \frac{8}{\sqrt{2}}\) find a5
Answer:
\(32 \sqrt{2}\)
Question 56.
Find AM of 24 and 16.
Answer:
20
Question 57.
In the Answer:P. – 11,-9, – 7, find d’.
Answer:
2
Question 58.
Which term of Answer:P. 21, 18, 15, …………… is -81 ?
Answer:
35th term
Question 59.
Write a G.P. your own with r = – 2.
Answer:
5,- 10, 20,-40, ……………
Question 60.
Find the sum of first ’n’ natural num-bers.
Answer:
1 + 2 + 3 + 4 ……………+ n = Σ \(\frac{\mathrm{n}(\mathrm{n}+1)}{2}\)
Question 61.
In AP a12 = 37, d = 3, then find S12.
Answer:
246
Explanation :
a12 = 37, d = 3
⇒ a + 11d = 37
⇒ a + 11 x 3 = 37
⇒ a = 37 – 33 = 4
S12 = \(\frac { 12 }{ 2 }\)[2 x 4 + 11 x 3]
= 6[8 + 33] = 6 x 41 = 246
Question 62.
If 3, x, 11 are in Answer:P., then find ‘x’.
Answer:
7 = x
Explanation :
x – 3 = 11- x ⇒ 2x = 14 ⇒ x = 7
Question 63.
In an AP 7a7 = 11a11, then find a18.
Answer:
0 = a18
Question 64.
Find number of terms of the Answer:P.
-5 + (-8) + (- 11) + + (-230).
Answer:
76
Explanation :
a = -5, d = -8 + 5 = -3, an ⇒ a + (n – 1) d = – 230
⇒ – 5 + (n – 1) (- 3) = – 230
⇒ (n – 1)(-3) = -225
⇒ n – 1 = \(\frac{-225}{-3}\) = 75
⇒ n = 75 + 1 ⇒ n = 76
Question 65.
– 8, – 6, – 4, find a7.
Answer:
6 = a7.
![]()
Question 66.
1, – 1, 1, – 1, 1, – 1, ………………upto 131 terms, then find S131.
Answer:
1 = S131.
Question 67.
ind the next term of the Answer:P. 51, 59, 67,75.
Answer:
83
Question 68.
an = 9 – 5n, find a4.
Answer:
-11
Explanation :
Explanation :
an = 9 – 5n
⇒ a4 = 9- 5×4 = 9-20 = -11
Question 69.
3, 6, 12, then find ‘r’.
Answer:
r = \(\frac{6}{3}=\frac{12}{6}\) = 2
Question 70.
Which term of Answer:P. 7 + 4 + 1 + is – 56 ?
Answer:
22
Question 71.
n – 1, n – 2, n – 3, ….. find a10.
Answer:
n – 10 = a10
Question 72.
Write Answer:M. of M, P, C.
Answer:
\(\frac{M+P+C}{3}\)
Question 73.
In the formula an = 3.6, a = – 18.9, d = 2.5, then find ‘n’.
Answer:
10
Explanation :
an = 3.6, a = – 18.9, d = 2.5
⇒ a + (n – 1)d = 3.6
⇒ – 18.9 + (n – 1)(2.5) = 3.6
⇒ (n – 1)(2.5) = 3.6 + 18.9 = 22.5
⇒ n-1 = \(\frac{22.5}{2.5}\) = 9
⇒ n = 9 + 1 = 10
Question 74.
Write G.M. of a’ arid \(\frac{1}{a}\).
Answer:
G.M. = 1
Question 75.
In a series an = \(\frac{n(n+1)}{3}\), find a2.
Answer:
a2 = 2.
Question 76.
If a, b, c are in Answer:P., then find b – Answer:
Answer:
c – b
Question 77.
\(\frac{1}{4}, \frac{-1}{4}, \frac{-3}{4}, \frac{-5}{4}\) ………….. find ‘d’
Answer:
d = \(\frac{-1}{2}\)
![]()
Question 78.
Find 1 + 1 + 1 + + n terms.
Answer:
Sn = n
Question 79.
Find G.M. of x3 and \(\frac{1}{x^{3}}\)
Answer:
G.M. = 1
Question 80.
Write Answer:M. of x2 + y2 and x2 – y2.
Answer:
x2
Explanation :
Answer:M = \(\frac{x^{2}+y^{2}+x^{2}-y^{2}}{2}=\frac{2 x^{2}}{2}\) = x2
Question 81.
a, a2, a3, …… then find r.
Answer:
r = a .
Question 82.
Reciprocals of terms of G.P. are in which progression ?
Answer:
G.P.
Question 83.
2, – 6, 18, – 54,………….find r.
Answer:
-3.
Question 84.
Find the value of – 5 + (- 8) + (- 11) + ………….. + (-230).
Answer:
-8930
Question 85.
In a G.P. 25, – 5,1, \(-\frac{1}{5}\),…. then find ‘r’.
Answer:
\(-\frac{1}{5}\) = r
Question 86.
If 2, x, 6 are in G.P., then find ‘x’.
Answer:
\(2 \sqrt{3}\) = x.
Question 87.
In a G.P. a8 = 192, r = 2, then find a12.
Answer:
3072 = a12.
Question 88.
Which term of G.P., 2,8,32, is 512?
Answer:
5
Question 89.
1, 2, 3, ……….. find sum to ’10’ terms.
Answer:
S10 = 55
Explanation :
a = 1,d = 1
S10 = \(\frac{10}{2}\)[21 + 9 x 1]
= 5[2 + 9] = 5 x 11 = 55
Question 90.
\(\frac{5}{2}, \frac{5}{4}, \frac{5}{8}\), …………. find an.
Answer:
\(\frac{5}{2^{n}}\) = an
Question 91.
4,16, , 256, ……….. then find
A,
64
![]()
Question 92.
In the Answer:P. 100, 103, 106, find d’.
Answer:
d = 3
Question 93.
Find the Answer:P. with first term is 8 and common difference is 2\(\frac { 1 }{ 2 }\).
Answer:
8, 10\(\frac { 1 }{ 2 }\), 13, …………….
Question 94.
How many terms of Answer:P. – 6, \(\frac { -11 }{ 2 }\), – 5, ……………. are needed to obtain a sum – 25 ?
Answer:
5 or 20 terms.
Explanation :
a = -6,d = \(\frac{-11}{2}\) + 6 = \(\frac{1}{2}\) Sn = -25
Sn = \(\frac{n}{2}\)[2a + (n – 1)d] = -25
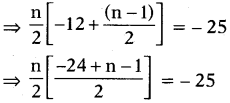
⇒ n (n – 25) – 100
⇒ n2 – 25n + 100 = 0
⇒ n2 – 20n – 5n + 100 = 0
⇒ n (n – 20) – 5 (n – 20) = 0
⇒ (n – 5) (n – 20) = 0
∴ n = 5 or 20
Question 95.
(a + 3d), (a + d), (a – d), ……….. find the next term of the Answer:P.
Answer:
a – 3d
Question 96.
Find the 103rd term of 1, -1,1,- 1, ….
Answer:
– 1
Question 97.
Find the sum of first 50 even numbers.
Answer:
2550
Explanation :
Sum of first 50 even numbers
= n(n + 1)
= 50(51) = 2550
Question 98.
Find the common ratio of the G.P.192, 36, 9, …………
Answer:
1/4
Question 99.
Find the 25th term of
– 300, – 290, – 280,
Answer:
-60.
Question 100.
a, b, c are in AP, then write, \(\frac{1}{a}, \frac{1}{b}, \frac{1}{c}\) are in which progression ?
Answer:
Harmonic progression (H.P)
Question 101.
In Answer:P. ap = q, aq = p, then find ap + q.
Answer:
0 = ap + q
Question 102.
a, b, c are in Answer:P., then 3a, 3b, 3c fire in which series ?
Answer:
In geometric Progression (G.P).
Question 103.
22, 32, 42, find a7.
Answer:
a7 = 82
![]()
Question 104.
an = 2n, then find a5.
Answer:
32 = a5.
Question 105.
Write G.M. of 5 and 125.
Answer:
25
Question 106.
Σn = 10, then Σn3.
Answer:
1000
Explanation :
(Σn)3 = (10)3 = 1000
Question 107.
Write G.M. of x, y, z.
Answer:
G.M. = \(\sqrt[3]{x y z}\)
Question 108.
Find the value of 16 + 11 + 6 + …. 23 terms.
Answer:
S23 = – 897.
Question 109.
Write a formula to 13 + 23 + 33 +….+ n3
Answer:
\(\frac{n^{2}(n+1)^{2}}{4}=\Sigma n^{3}\)
Question 110.
an = (n – 1) (n – 2), then find a2.
Answer:
a2 = 1
Question 111.
If a, b, c are in G.P., then find \(\frac{\mathbf{b}}{\mathbf{a}}\)
Answer:
\(\frac{b}{a}=\frac{c}{b}\)
Question 112.
-1, \(\frac{1}{4}, \frac{3}{2}\), ……….. find sum to 10 terms.
Answer:
46.25
Question 113.
Find the sum of first 40 positive integers which are divisible by 6.
Answer:
4920
Explanation :
Sn = 6 + 12 + 18 + 24 + …. + 240
= \(6\left[\frac{\mathrm{n}(\mathrm{n}+1)}{2}\right]=6\left[\frac{40 \times 41}{2}\right]\)
= 6 x 20 x 41
= 4920
Question 114.
If a, b, c are in G.P., then find b2.
Answer:
ac = b2
Question 115.
Calculate the common ratio of the G.P. 4, 20, 100, 500, ……………
Answer:
r = 5
![]()
Question 116.
In the Answer:P., first term is 4 and common difference is – 1, then find Answer:P.
Answer:
4,3, 2, Answer:P.
Question 117.
Find the sum of first 20 odd numbers..
Answer:
400 = S20.
Question 118.
How many numbers are divisible by ‘4’ lying between 101 and 250 ?
Answer:
37
Question 119.
If a7 – a3 = 32, then the common dif-ference of the Answer:P.
Answer:
8 = d
Question 120.
Which term of the Answer:P. 125, 120, 115, ………… is the first negative ?
Answer:
7th term.
Question 121.
If a7 ÷ a4 of a G.P is 343, then find the common ratio.
Answer:
r = 7.
Question 122.
If x, xy, xy2, xy3, …. forms a G.P, then find its 15th term.
Answer:
xy14
Question 123.
Find the nth term of a, a + d, a + 2d,…
Answer:
a + (n – 1) d = an
Question 124.
In a G.P. write a6.
Answer:
ar5 = a6.
Question 125.
Calculate the 16th term of 4, – 4, 4, – 4, ……..
Answer:
4 = a6.
Question 126.
In Answer:P. aa12. = 37, d = 3, then find ‘a’.
Answer:
4 = Answer:
Question 127.
3, – 32, 33, find a6.
Answer:
– 729 = a6.
Question 128.
If there are’n’AM’s between’a’and h’, then find d.
Answer:
d = \(\frac{b-a}{n+1}\)
![]()
Question 129.
7, 10, 13, find a5.
Answer:
19 = a5.
Question 130.
Find AM of 5 and 95.
Answer:
50 = AM
Question 131.
f 4, x, 16 are in G.P., then find ‘x’.
Answer:
8
Explanation :
b2 = ac ⇒ x = \(\sqrt{4 \times 16}=\sqrt{64}\) = 8
Question 132.
5, 1, – 3, – 7, find a10.
Answer:
– 31 = a10.
Question 133.
Write product of ‘n’ GM’s between a and b.
Answer:
(ab)n/2 = G.M.
Question 134.
If a, b, c are in GP, then b is called
Answer:
Geometric mean.
Question 135.
How many 3-digit numbers are divisible by 7 ?
Answer:
128
Question 136.
If a = 3 and a7 = 33, then find a11.
Answer:
53 = a11
Explanation :
a = 3,
a7 = a + (n – 1)d = 33
⇒ 3 + (7 – 1) d = 33
⇒ 6d = 30 ⇒ d = 5
a11 = a + 10d
= 3 + 10×5 = 3 + 50 = 53
Question 137.
Find the 10th term of the
AP:3, 11, 19, …………..
Answer:
75 = a10
![]()
Question 138.
aa28 – aa23 = 15, then find the common difference of the Answer:P.
Answer:
3 = d
Question 139.
If x – 1, x + 3, 3x – 1 are in Answer:P., then find ‘x’.
Answer:
4 = x
Question 140.
Find the common ratio of the G.P.
3, 6, 12, 24, …………..
Answer:
2
Question 141.
Find the 8th term from the end of the Answer:P., 7, 10, 13, …………. 1814.
Answer:
163
Question 142.
\(\frac{\mathbf{b}+\mathbf{c}-\mathbf{a}}{\mathbf{a}}, \frac{\mathbf{c}+\mathbf{a}-\mathbf{b}}{\mathbf{b}}, \frac{\mathbf{a}+\mathbf{b}-\mathbf{c}}{\mathbf{c}}\) are in AP, then write \(\frac{1}{a}, \frac{1}{b}, \frac{1}{c}\) are in ,
Answer:
Arithmetic Progression.
Question 143.
Which term of the Answer:P, 24, 21, 18, …. is the first negative ?
Answer:
a10 is first negative term.
Question 144.
Find AM of 10 and 20.
Answer:
15 = AM .
Question 145.
Write the next term of the
Answer:P. \(\sqrt{48}, \sqrt{75}, \sqrt{147}, \ldots \ldots \ldots\)
Answer:
\(\sqrt{192}\)
Question 146.
– 20, – 18, – 16, ………… which term of this Answer:P. is a first positive term ?
Answer:
12
Question 147.
Find the 17th term of 1.1, 2.2, 3.3, 4.4 …………….
Answer:
18.7 = a17
Question 148.
If \(\frac{a^{n+1}+b^{n+1}}{a^{n}+b^{n}}\) is the AM of ‘a’and ‘b’, then find ‘n’.
Answer:
n = 0.
Choose the correct answer satisfying the following statements.
Question 149.
Statement (A): Common difference of the AP : – 5, – 1, 3, 7, is 4.
Statement (B): Common difference of the a, a + d, a + 2d, is given by
d = 2nd term – 1st term.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)
Explanation :
Common difference, d = – 1 – (- 5)
= 4
So, both A and B are correct and B explains Answer: Hence, (i) is the correct option.
![]()
Question 150.
Statement (A) : an – an-1 is not independent of n, then the given sequence is an AP.
Statement (B) : Common difference d = an – an-1 is constant or independent of n.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(iii)
Explanation :
We have, common difference of an Answer:P. d = an – an-1 is independent of ‘n’ or constant. So, A is incorrect but B is correct. Hence, (iii) is the correct option.
Question 151.
Statement (A): The sum of the first ‘n’ terms of an AP is given by Sn = 3n2 -4n. Then its nth term an = 6n – 7.
Statement (B) : nth term of an AP, whose sum to ’n’ terms is Sn, is given
by an = Sn – Sn-1
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)
Explanation :
nth term of an AP be an = Sn – Sn-1
⇒ an = 3n2 – 4n – 3(n – 1)2 + 4 (n – 1)
⇒ an = 6n – 7
So, both A and B are correct and B explains Answer: Hence, (i) is the correct option.
Question 152.
Statement (A) : Common difference of an AP in which a21 – a7 = 84 is 14. Statement (B) : nth term of an AP is given by an = a + (n – 1) d.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(iii)
Explanation :
We have, an= a + (n – 1)d
a21 – a7 = {a + (21 – 1)}d – {a + (7-l)d} = 84
⇒ a + 20d – a – 6d = 84
⇒ 14d = 84
⇒ d = 84/14 = 6
⇒ d = 6
So, A is incorrect but B is correct. Hence, (iii) is the correct option.
Question 153.
Statement (A) : Three consecutive terms 2k + 1, 3k + 3 and 5k – 1 from an AP, then k is equal to 6.
Statement (B) : In an AP
a, a + d, a + 2d, the sum to n terms of the AP be Sn = \(\frac{\mathrm{n}}{2}\) [2a + (n – 1)d].
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)
Explanation :
For 2k + 1, 3k + 3 and 5k- 1 to form an Answer:P.
(3k + 3)-(2k + 1) = (5k- l)-(3k + 3)
⇒ k + 2 = 2k-4
⇒ 2 + 4 = 2k – k = k
⇒ k = 6
So, both A and B are correct but B does not explain Answer:
Hence, (i) is the correct option.
Question 154.
Statement (A) : 10th term from the end of AP : 100, 95, 90, 85,……………. 10 is 55.
Statement (B): The nth term from the end of an AP having last term L and common difference d is L – (n – 1) d.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)
![]()
Question 155.
Statement (A) : If the sum of first ‘n’ terms of an AP is an2 + bn, then its common difference is 2Answer:
Statement (B): In an AP with first term a and last term l, sum of n terms is
given by Sn = \(\frac{n}{2}\)(a + l).
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(iii)
Question 156.
Statement (A) : The sum of all natural numbers between 100 and 1000 which are multiple of 7 is 70336.
Statement (B) : The 10th term of an AP is 31 and 20th term is 71. Then t30 = 111
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(ii)
Question 157.
Statement (A): 1, 2, 4, 8,……………. is a G.P., 4, 8, 16, 32 is a G.P. and 1 + 4, 2 + 8, 4 + 16, 8 + 32, …. is also a G.P.
Statement (B) : Let general term of a G.P. with common ratio ‘r’ be Tk + 1 and general term of another G.P., with common ratio ‘r’ be Tk + v then the series
whose general term Tk + 1 = Tk + 1 + Tk + 1 is also a G.P. with common ratio ‘r’.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)
Explanation :
Let Tk + 1 = ark and Tk + 1 = brk
Since T”k + 1 = ark + brk = (a + b)rk ,
∴ T”k + 1 is general term of a G.P.
Option (i) is correct.
Question 158.
Statement (A) : 1111 …………. 1 (upto 91 terms) is a prime number.
Statement (B) : If \(\frac{b+c-a}{a}\), \(\frac{c+a-b}{b}, \frac{a+b-c}{c}\) are in Answer:P., then \(\frac{1}{a}, \frac{1}{b}, \frac{1}{c}\) are also in Answer:P.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(iii)
Explanation :
Since 11 11 ………..,
= \(\frac{10^{91}-1}{10-1}\) = divisible by 9.
The given number is not prime. So, A is false, but B is true.
∴ Option (iii) is correct.
Question 159.
Statement (A) : Let the positive numbers a, b, c be in Answer:P, then \(\frac{1}{\mathrm{bc}}, \frac{1}{\mathrm{ac}}, \frac{1}{\mathrm{ab}}\) are also in Answer:P.
Statement (B): If each term of an Answer:P. is divided by abc, then the resulting sequence is also in Answer:P.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)
Question 160.
Statement (A) : Let three distinct positive real numbers a, b, c are in G.P., then a2, b2, c2 are in G.P.
Statement (B) : If we square each term of a G.P., then the resulting sequence is also in G.P.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)
Question 161.
Statement (A) : The sum of the series with the nth term, tn = (9 – 5n) is 465, when number of terms n = 15.
Statement (B) : Given series is in Answer:P. and sum of ‘n’ terms of an Answer:P. is
Sn = \(\frac{\mathrm{n}}{2}\)[2a + (n- 1) d]
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(iii)
Read Che below passages and answer to the following questions.
Following given series are in Answer:P.
2, 4, 6, 8, …………..
3,6,9,12, ……….
First series contains 30 terms, while the second series contains 20 terms. Both of the above given series contains some terms, which are common to both of them.
![]()
Question 162.
Find the last term of both the above given Answer:P. are
Answer:
(60, 60)
Explanation :
For 2, 4, 6, 8, …………..
Last term, t30 = 2 + (30 – 1)2
= 2 + 2 (29) = 60
3,6,9,12,
Last term, t20 = 3 + (20 – 1)3 x = 3 + 57 = 60
Question 163.
Find the sum of both the above given Answer:P. are
Answer:
(930, 630).
Explanation :
For 2, 4, 6, 8,
S30 = \(\frac { 30 }{ 2 }\) (2 + 60) = 930
For 3, 6, 9, 12,
S20 = \(\frac { 20 }{ 2 }\) (3 + 60) = 630
Question 164.
Write number of terms identical to both the above given Answer:P. are
Answer:
10
Explanation :
Let mth term of the first series is common with the nth term of the second series.
tm = tn
2 + (m – 1)2 = 3 + (n – 1) 3
2 + 2m -2 = 3 + 3n – 3
2m = 3n
\(\frac{m}{3}=\frac{n}{2}=k \text { (let) }\)
m = 3k, n = 2k.
Hence, k = 1, 2, 3, , 10.
[ ∵ 1 ≤ m ≤ 30, 1 ≤ n ≤ 20
1 ≤ 3k ≤ 30, 1 ≤ 2k ≤ 20
\(\frac{1}{2}\) ≤ k ≤ 10, \(\frac{1}{2}\) ≤ k ≤ 10]
For each value of k, we get one identical term.
Thus, number of identical terms =10.
There are 25 trees at equal distances of 5 m in a line with a well, the distance of the well from the nearest tree being 10 m. A gardener waters all the trees separately starting from the well and he returns to the well after watering each tree to get water for the next.
Question 165.
Where the well located in the garden?
Answer:
Obviously the well must be on one side of the trees.
Question 166.
How much the distance between the trees ?
Answer:
5 m.
Question 167.
Which mathematical concept is used to find the total distance the gardener will cover in order to water all the trees?
Answer:
Arithmetic Progression.
Question 168.
Column – II give common difference for Answer:P. given column -1, match them cor-rectly.

Answer:
A – (iv), B – (iii).
Question 169.
Column – II give common difference for Answer:P. given column -1, match them cor. rectly.

Answer:
A – (ii), B – (i).
![]()
Question 170.
Column – II give nth term for Answer:P. given column -I, match them correctly.

Answer:
A – (iv), B – (iii).
Question 171.
Column – II give n,h term for Answer:P. given column -I, match them correctly.

Answer:
A – (ii), B – (i).
Question 172.

Answer:
A – (i), B – (ii).
Question 173.

Answer:
A – (iv), B – (iii).
Question 174.
In which progression are the perimeters of triangles formed by joining the midpoints of sides of triangles succes-sively in the given figure.

Answer:
Geometric Progression.