Bit Bank

Andhra Pradesh SCERT AP State Board Syllabus SSC 10th Class Maths Important Bits with Answers in English and Telugu Medium are part of AP SSC 10th Class Textbook Solutions.

Students can also read AP SSC 10th Class Maths Solutions for board exams.

AP State Syllabus 10th Class Maths Important Bits with Answers in English and Telugu

Maths Bits for 10th Class

1. Real Numbers Bits for 10th Class
2. Sets Bits for 10th Class
3. Polynomials Bits for 10th Class
4. Pair of Linear Equations in Two Variables Bits for 10th Class
5. Quadratic Equations Bits for 10th Class
6. Progressions Bits for 10th Class
7. Coordinate Geometry Bits for 10th Class
8. Similar Triangles Bits for 10th Class
9. Tangents and Secants to a Circle Bits for 10th Class
10. Mensuration Bits for 10th Class
11. Trigonometry Bits for 10th Class
12. Applications of Trigonometry Bits for 10th Class
13. Probability Bits for 10th Class
14. Statistics Bits for 10th Class

10th Class Maths Bits in Telugu Medium

• 1st Lesson వాస్తవ సంఖ్యలు Bits
• 2nd Lesson సమితులు Bits
• 3rd Lesson బహుపదులు Bits
• 4th Lesson రెండు చరరాశులలో రేఖీయ సమీకరణాల జత Bits
• 5th Lesson వర్గ సమీకరణాలు Bits
• 6th Lesson శ్రేఢులు Bits
• 7th Lesson నిరూపక రేఖాగణితం Bits
• 8th Lesson సరూప త్రిభుజాలు Bits
• 9th Lesson వృత్తాలకు స్పర్శరేఖలు మరియు ఛేదనరేఖలు Bits
• 10th Lesson క్షేత్రమితి Bits
• 11th Lesson త్రికోణమితి Bits
• 12th Lesson త్రికోణమితి అనువర్తనాలు Bits
• 13th Lesson సంభావ్యత Bits
• 14th Lesson సాంఖ్యక శాస్త్రం Bits

AP State Syllabus Bits with Answers

Practice the AP 9th Class Maths Bits with Answers Chapter 8 Quadrilaterals on a regular basis so that you can attempt exams with utmost confidence.

AP State Syllabus 9th Class Maths Bits 8th Lesson Quadrilaterals with Answers

Choose the correct answer :

Question 1.
The sum of the four interior angles of a quadrilateral is
A) 360 right angles
B) 4 right angles
C) 2 right angles
D) right angle
Answer:
B) 4 right angles

Question 2.
A quadrilateral in which one pair of opposite sides are parallel is a
A) parallelogram
B) kite
C) trapezium
D) rhombus
Answer:
C) trapezium

Question 3.
In the figure ∠D =

A) 110°
B) 70°
C) 60°
D) 120°
Answer:
D) 120°

Question 4.
□ABCD is a trapezium in which AB//CD. If ∠A = 45° then ∠D =

A) 45°
B) 55°
C) 135°
D) 125°
Answer:
C) 135°

Question 5.
□ABCD is a parallelogram. If ∠D = 80° then ∠A, ∠B, ∠C are
A) 80°, 100°, 100°
B) 100°, 80°, 100°
C) 80°, 100°, 80°
D) 100°, 80°, 80°
Answer:
B) 100°, 80°, 100°

Question 6.
□ABCD is a parallelogram and BC is extended. If ∠A = 40° then ∠DCE =

A) 40°
B) 140°
C) 50°
D) 60°
Answer:
A) 40°

Question 7.
The bisectors of any two interior angles of a rhombus meet at
A) accute angle
B) right angle
C) obtuse angle
D) none
Answer:
B) right angle

Question 8.
Diagonals are equal in a
A) rhombus
B) quadrilateral
C) parallelogram
D) rectangle
Answer:
D) rectangle

Question 9.
Angle between the diagonals of a rhombus is
A) acute
B) obtuse
C) right angle
D) none
Answer:
C) right angle

Question 10.
In a parallelogram ABCD, ∠BAD = 65° then ∠ADC =

A) 25°
B) 115°
C) 65°
D) 35°
Answer:
C) 65°

Question 11.
Each angle of a rectangle is
A) right angle
B) acute angle
C) obtuse angle
D) reflex angle
Answer:
A) right angle

Question 12.
In parallelogram ABCD the bisectors of ∠A and ∠B meet at ’O’. Then the value of x° is

A) 180°
B) 90°
C) 60°
D) can’t be determined
Answer:
B) 90°

Question 13.
In ΔABC, BC = 8 cm and D, E are the midpoints of AB and AC; also AF = \(\frac{1}{2}\)AD and AG = \(\frac{1}{2}\)AE then FG =

A) 4 cm
B) 32 cm
C) 3 cm
D) 2 cm
Answer:
D) 2 cm

Question 14.
In ΔABC; D, E and F are the mid points of the sides, then ΔDEF =

A) \(\frac{1}{3}\)ΔABC
B) \(\frac{1}{2}\)ΔABC
C) \(\frac{1}{4}\)ΔABC
D) 3ΔABC
Answer:
C) \(\frac{1}{4}\)ΔABC

Question 15.
If the diagonals of a quadrilateral bisect each other then it is a
A) rhombus
B) parallelogram
C) square
D) rectangle
Answer:
B) parallelogram

Question 16.
Two adjacent sides of a parallelogram are 4.7 cm and 6.3 cm then its perimeter is
A) 11 cm
B) 5.5 cm
C) 22 cm
D) 29.51 cm
Answer:
C) 22 cm

Question 17.
If each pair of opposite angles are equal then it is a
A) rectangle
B) square
C) trapezium
D) parallelogram
Answer:
D) parallelogram

Question 18.
In □ABCD; AB = DC and AD = BC also ∠A = 90° then □ABCD is a
A) rectangle
B) square
C) parallelogram
D) rhombus
Answer:
A) rectangle

Question 19.
The figure formed by joining the midpoints of sides of a rectangle is
A) square
B) rhombus
C) rectangle
D) parallelogram
Answer:
B) rhombus

Question 20.
The figure formed by joining the mid-points of sides of a rhombus is
A) rhombus
B) rectangle
C) parallelogram
D) square
Answer:
B) rectangle

Question 21.
The sum of four angles of a quadrilateral is
A) 2 right angles
B) 3 right angles
C) 4 right angles
D) 8 right angles
Answer:
C) 4 right angles

Question 22.
One of the diagonals of the quadrilateral ABCD is
A) AB
B) AC
C) BC
D) CD
Answer:
B) AC

Question 23.
The opposite vertices of the quadrilateral PQRS are
A) P, Q
B) Q, R
C) R, S
D) Q, S
Answer:
D) Q, S

Question 24.
If a parallelogram has all its angles as right angles, then it is a
A) rectangle
B) rhombus
C) square
D) trapezium
Answer:
A) rectangle

Question 25.
In a parallelogram ABCD, if ∠DAB = 50°, then ∠ABC =

A) 100°
B) 25°
C) 130°
D) 50°
Answer:
C) 130°

Question 26.
Two given sides of a parallelogram are 8 cm and 3 cm, then its perimeter is
A) 11 cm
B) 22 cm
C) 24 cm
D) 14 cm
Answer:
B) 22 cm

Question 27.
In a parallelogram, which of the following is true?
A) All sides are equal
B) Each angle is 90°
C) Diagonals are equal
D) Diagonals bisect each other
Answer:
D) Diagonals bisect each other

Question 28.
Which of the following statements is false?
A) Every parallelogram is a trapezium.
B) All trapeziums are parallelograms.
C) All parallelograms are quadrilaterals.
D) A square is a rhombus.
Answer:
B) All trapeziums are parallelograms.

Question 29.
If each pair of opposite sides of a quadrilateral is equal, then it is a
A) Parallelogram
B) Rhombus
C) Isosceles trapezium
D) Trapezium
Answer:
A) Parallelogram

Question 30.
A diagonal of a parallelogram divides it into two
A) Equal triangles
B) Similar triangles
C) Congruent triangles
D) Right triangles
Answer:
C) Congruent triangles

Question 31.
The given figure ABCD is a parallelogram. Diagonals intersect at ‘O’, then

A) ∠AOB = ∠OAB
B) ∠ACD = ∠CAB
C) OA = OB
D) ∠AOD = ∠AOB
Answer:
B) ∠ACD = ∠CAB

Question 32.
The angle bisectors of a parallelogram form a
A) Square
B) Rectangle
C) Parallelogram
D) Rhombus
Answer:
B) Rectangle

Question 33.
In the parallelogram PQRS, ∠P = 40°, then ∠R =
A) 40°
B) 50°
C) 140°
D) 80°
Answer:
A) 40°

Question 34.
The ratio of two consecutive angles of a parallelogram is 1 : 2, then the greater angle is
A) 60°
B) 30°
C) 120°
D) 150°
Answer:
C) 120°

Question 35.
ΔABC is an equilateral triangle. D, E are the mid points of AB and AC respectively. If DE = 3 cm, then the perimeter of ΔABC is

A) 9 cm
B) 12 cm
C) 15 cm
D) 18cm
Answer:
D) 18cm

Question 36.
ABCD is a parallelogram. If ∠BAD = 110°, then ∠DCE =

A) 70°
B) 55°
C) 35°
D) 60°
Answer:
A) 70°

Question 37.
In the parallelogram PQRS, \(\frac{1}{2}\)∠P + \(\frac{1}{2}\)∠Q =
A) 180°
B) 120°
C) 90°
D) 60°
Answer:
C) 90°

Question 38.
In the given figure, AC ⊥ BD and AC ≠ BD, then ABCD is a

A) Square
B) Rhombus
C) Rectangle
D) Parallelogram
Answer:
B) Rhombus

Question 39.
ABC is an equilateral triangle with side 10 cm. The perimeter of the triangle formed by joining the mid points of the sides of ΔABC is
A) 30 cm
B) 20 cm
C) 15 cm
D) 5 cm
Answer:
C) 15 cm

Question 40.
The quadrilateral in which the diagonals are equal but not perpendicular to each other is
A) Square
B) Rhombus
C) Parallelogram
D) Rectangle
Answer:
D) Rectangle

Question 41.
Statement – 1: In a parallelogram, two adjacent angles are equal then it is called Rectangle.
Statement – 2: If one angle of Rhombus is right angle then it’s square.
A) Both 1 & 2 are true
B) Both 1 & 2 are false
C) 1 is true & 2 is false
D) 1 is false & 2 is true
Answer:
A) Both 1 & 2 are true

Question 42.
If one of the angles of the quadrilateral is 120° and the remaining three angles are equal then the measure of each angle is
A) 120°
B) 80°
C) 60°
D) 40°
Answer:
B) 80°

Question 43.
Among the following the correct statement is………………
i) A Rhombus is a Square
ii) Product of two odd integers even
iii) All even numbers are composite
iv) 3 is a prime
A) i and iii
B) ii and iv
C) only ii
D) only iv
Answer:
D) only iv

Question 44.
In a Trapezium ABCD, if \(\overline{\mathbf{A B}}\) || \(\overline{\mathbf{D C}}\) and ∠D = x° then ∠A = ?
A) 180 – x°
B) 90 – x°
C) x°
D) 360 – x°
Answer:
A) 180 – x°

Question 45.
From the adjacent figure, PQ || RS, ∠RPQ = 52°, ∠RPS = 65°, ∠PSR = x° and ∠PRQ = 3y° + 5, then the value of x + y is

A) 115°
B) 137
C) 200
D) 74
Answer:
A) 115°

Question 46.
Opposite angles of a cyclic quadrilateral are………………….
A) Complimentary
B) Supplementary
C) Conjugate
D) Reflective
Answer:
B) Supplementary

Question 47.
Match the following.

A) (K, 1) (L, 2) (M, 3)
B) (K, 3) (L, 1) (M, 2)
C) (K, 2) (L, 1) (M, 3)
D) (K,3)(L, 2)(M, 1)
Answer:

Question 48.
The area of a parallelogram whose base is ‘b’ units, height is ‘h’ units (in sq. units)
A) bh
B) \(\frac{1}{2}\)bh
C) \(\frac{1}{2}\) × d₁ × d₂
D) \(\frac{1}{2}\) × h (a + b)
Answer:
A) bh

Question 49.
If the perimeters of a square and rectangle are equal, then
A) Both the areas are equal
B) Area of square is more than area of rectangle.
C) Area of rectangle is more than area of square.
D) Area of square is less than area of rectangle.
Answer:
A) Both the areas are equal

Question 50.
In a parallelogram, if one set of opposite angles are complementary, then the biggest angle in it is
A) 270°
B) 45°
C) 90°
D) 135°
Answer:
D) 135°

Question 51.
In the given figure AB || CD, AB = CD, \(\overline{\mathbf{A C}}\) and \(\overline{\mathbf{B D}}\) intersects at O. From the given information which of these is false?

A) ΔABC ≅ ΔBDC
B) ∠OBA = ∠ODC
C) ΔOAB ≅ ΔOCD
D) ‘O’ is the bisecting point of \(\overline{\mathbf{A C}}\), \(\overline{\mathbf{B D}}\)

→ Read the following information and answer the questions from 12 to 16.
Name of Quadrilateral – Properties
1. □ ABCD Only one set of opposite sides are parallel.
2. □ PQRS Diagonals bisects at each other.
3. □ KLMN All the sides and angles are qual.
Answer:
A) ΔABC ≅ ΔBDC,
D) ‘O’ is the bisecting point of \(\overline{\mathbf{A C}}\), \(\overline{\mathbf{B D}}\)

Question 52.
In □ ABCD if BC || AD, and \(\overline{\mathbf{B D}}\) is a transversal, ∠ADB = 100° – 4x°,
∠CBD = 180° – 5x°, then x° = …………………..
A) 270°
B) 80°
C) 100°
D) 180°
Answer:
B) 80°

Question 53.
In □ KLMN, KM is the diagonal, then ∠KML = ……………….
A) 180°
B) 45°
C) 90°
D) 135°
Answer:
B) 45°

Question 54.
In □ PQRS, \(\overline{\mathbf{P X}}\) and \(\overline{\mathbf{Q Y}}\) are the angle bisectors at P, ∠Q which meets at O, then ∠POQ = …………………….
A) 180°
B) 45°
C) 90°
D) 135°
Answer:
C) 90°

Question 55.
Which of the following is not correct?
A) In □ KLMN diagonals are equal
B) All the properties of □ PQRS hold good for □ KLMN
C) All the angles are equal in □ PQRS
D) All the properties of □ KLMN hold good for □ PQRS
Answer:
C) All the angles are equal in □ PQRS

Question 56.
In □ ABCD if \(\overline{\mathbf{A B}}\) || \(\overline{\mathbf{C D}}\) , then ∠A and ∠D are
A) Linear pair to each other
B) Complementary to each other
C) Supplementary to each other
D) Conjugate angles to each other
→ Read the following information and answer 17-21 :
In the parallelogram ABCD, X, Y are the mid points of \(\overline{\mathbf{C D}}\), \(\overline{\mathbf{A D}}\) respectively. Area of □ ABCD is 64 cm².

Answer:
C) Supplementary to each other

Question 57.
If AB =16 cm, then the distance between \(\overline{\mathbf{A B}}\), \(\overline{\mathbf{C D}}\) is
A) 16
B) 4
C) 8
D) 8.5
Answer:
B) 4

Question 58.
Area of Δ CYD : Area of □ ABCD is
A) 1 : 5
B) 1 : 2
C) 1 : 3
D) 1 : 4
Answer:
B) 1 : 2

Question 59.
If X and Y are joined and A and C are joined, then the area of trapezium □ XYAC Cm cm²)
A) 28
B) 4
C) 16
D) 24
Answer:
C) 16

Question 60.
In the given figure which one is wrong?
A) Area of ΔBAY = Area of ΔBCX
B) Area of ΔDAX + Area of ΔBCX = Area of ΔABX
C) Area of ΔBCY = \(\frac{1}{2}\) Area of □ ABCD
D) ΔDCY ≅ ΔBAY
Answer:
D) ΔDCY ≅ ΔBAY

Question 61.
Which of the following are in the same ratio as Area of □ ABXD : Area of □ ABCD?
A) Both Area of □ABCX: Area of □ABCD and Area of □ABCY : Area of □ABCD.
B) Area of □ABCX : Area of □ABCD
C) Area of □ABCY : Area of □ABCD
D) Area of □ABCD : Area of □BCDY
Answer:
B) Area of □ABCX : Area of □ABCD

Question 62.
In the given quadrilateral □ PQRS, PR, QS are the diagonals intersecting at ‘O’. From the given information which figure are congruent?

A) ΔORS ≅ ΔOPS
B) ΔOPQ ≅ ΔOQR
C) ΔOQR ≅ ΔORS
D) ΔPQS ≅ ΔQRS
Answer:
D) ΔPQS ≅ ΔQRS

Question 63.
From the given figure ΔKLM ≅ ΔKMN (A.S.A. rule) under CPCT ML =

A) MK
B) KL
C) MN
D) KN
Answer:
D) KN

Question 64.
From a rectangular shape of paper if you cut 3 triangles the area of biggest triangle is
A) Equal in areas
B) \(\frac{1}{4}\)^th area of rectangle
C) \(\frac{1}{2}\)^th area of rectangle
D) \(\frac{3}{4}\)^th area of rectangle
Answer:

Question 65.
In the given figure □ ABHI, □ BCDE, QACGF are parallelograms. Which among these is bigger in area?

A) All are equal
B) □ ABHI
C) □ BCDE
D) □ ACGF
Answer:
A) All are equal

Question 66.
In a rhombus a diagonal divides it into
A) Two equilateral triangles.
B) Two right angled triangles.
C) Two scalened triangles.
D) Two isosceles triangles.
Answer:
B) Two right angled triangles.

Question 67.
The opposite angles of a parallelogram are (3x – 20)° and (x + 70)° then the value of x.
A) 60°
B) 55°
C) 45°
D) 30°
Answer:
C) 45°

Question 68.
The figure formed by joining the midpoints of sides of parallelogram
A) Rhombus
B) Square
C) Parallelogram
D) Rectangle
Answer:
C) Parallelogram

Question 69.
ABCD is a parallelogram. \(\overline{\mathbf{A O}}\) and \(\overline{\mathbf{B O}}\) are bisectors of ∠A and ∠B, then ∠AOB =

A) 90°
B) 120°
C) 180°
D) 360°
Answer:
A) 90°

Question 70.
The points A, B, C and D on a circle form a quadrilateral ABCD. If ∠A = 45° then measure of ∠C =
A) 45°
B) 135°
C) 225°
D) 315°
Answer:
B) 135°

Question 71.
The side of a rhombus is 4 cm. What is its perimeter?
A) 8 cm
B) 12 cm
C) 16 cm
D) 20 cm
Answer:
C) 16 cm

Question 72.
Which of the following statement is FALSE?
A) All rectangles are parallelogram
B) All squares are parallelogram
C) All rhombus are parallelogram
D) All trapeziums are parallelogram
Answer:
D) All trapeziums are parallelogram

Question 73.
Which of the following quadrilateral satisfies the following two conditions?
i) Opposite sides are equal and adja-cent sides are unequal.
ii) Opposite angles are equal and ad-jacent angles are unequal.
A) Rectangle
B) Square
C) Parallelogram
D) Rhombus
Answer:
C) Parallelogram

Question 74.
Which of the following is TRUE?

A) P is convex & Q is convex
B) P is convex & Q is concave
C) P is concave & Q is convex
D) P is concave & Q is concave
Answer:
A) P is convex & Q is convex

Practice the AP 9th Class Maths Bits with Answers Chapter 9 Statistics on a regular basis so that you can attempt exams with utmost confidence.

AP State Syllabus 9th Class Maths Bits 9th Lesson Statistics with Answers

Choose the correct answer :

Question 1.
Information collected in the form of facts, numerical figures, tables etc., is called
A) mean
B) median
C) mode
D) data
Answer:
D) data

Question 2.
Data collected from a source like registers is called
A) primary data
B) secondary data
C) pictograph
D) bar graph
Answer:
B) secondary data

Question 3.
Range of the data “18, 24, 15, 17, 33, 16, 29, 45, 12, 3, 33, 21” is
A) 33
B) 42
C) 48
D) 30
Answer:
B) 42

Question 4.
0 – 10, 11 – 20, 21 – 30, 31 – 40. The real lower limit of the class 21 – 30 is
A) 21
B) 30
C) 20.5
D) 21.5
Answer:
C) 20.5

Question 5.
In the above problem, the classes are called
A) inclusive
B) exclusive
C) continuous
D) none
Answer:
A) inclusive

Question 6.
The temperatures of a city recorded during a week are 42°, 35°, 44°, 33°, 39°, 45° and 42°. The average temperature is
A) 42°
B) 35°
C) 39°
D) 40°
Answer:
D) 40°

Question 7.

The mean of the above table is
A) 2.9
B) 3.9
C) 4.9
D) 3.7
Answer:
B) 3.9

Question 8.
In a deviation problem Σf_id_i = – 12 and A = 15; Σf = 20 then \(\overline{\mathbf{x}}\) =
A) 15.6
B) 14.6
C) 14.4
D) 12.4
Answer:
C) 14.4

Question 9.
Median of 3, 7, 4, 6 and 12 is
A) 7
B) 6
C) 4
D) 12
Answer:
B) 6

Question 10.
Median of the data 5,8, 9, x, 11, 13 is 9.5 (given that data is arraned in ascending order) then x is
A) 8
B) 9.5
C) 10
D) 10.5.
Answer:
C) 10

Question 11.
Formula to find mean for a grouped data is
A) A + \(\frac{\Sigma \hat{f}_{i} \mathrm{~d}_{\mathrm{i}}}{\mathrm{f}_{\mathrm{i}}}\)
B) A + \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{d}_{\mathrm{i}}}{\mathrm{C}}\)
C) A + \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{d}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\) × C
D) None
Answer:
A) A + \(\frac{\Sigma \hat{f}_{i} \mathrm{~d}_{\mathrm{i}}}{\mathrm{f}_{\mathrm{i}}}\)

Question 12.
Mode of the data 3, 7,8, 8, 7,6, 8, 4, 3, 11 is
A) 3
B) 7
C) 8
D) 11
Answer:
C) 8

Question 13.
Mean of the data x₁, x₂, x₃, x₄, x₅ is 15. If each observation is multiplied 3 then the mean becomes
A) 5
B) 45
C) 18
D) 12
Answer:
B) 45

Question 14.
If the mean of the data 12, 8, 6, 3, 9 is 7.6. If 5 is added to each observation then the new mean is
A) 2.6
B) 32.6
C) 12.6
D) 13.6
Answer:
C) 12.6

Question 15.
Mean of the data 8, 7, 6, 14, 12, 10, 20, 16, 15 and 14 is 12.2. If each observation is multiplied by 2 and then 3 is added, the new mean is
A) 38.6
B) 61
C) 27
D) 27.4
Answer:
D) 27.4

Question 16.
In the above problem the new median is
A) 29
B) 41
C) 40
D) 28
Answer:
A) 29

Question 17.
The median of n observations arranged in ascending order when n is even
A) \(\frac{\mathrm{n}}{2}\) observation
B) \(\frac{\mathrm{n}}{2}\) + 1 observation
C) average of \(\frac{\mathrm{n}}{2}\) and \(\frac{\mathrm{n}}{2}\) + 1 observations
D) none
Answer:
C) average of \(\frac{\mathrm{n}}{2}\) and \(\frac{\mathrm{n}}{2}\) + 1 observations

Question 18.
A data having two modes is
A) unimodal data
B) bi-modal data
C) tri modal data
D) none
Answer:
B) bi-modal data

Question 19.
The mode of the data 8,5, 3, 8,3,6, 5, 3, 7, 5 and 11 is
A) 5
B) 8
C) 3
D) 5 and 3
Answer:
D) 5 and 3

Question 20.
The difference between any two lower limits is called
A) size of the class
B) range
C) frequency
D) upper limit
Answer:
A) size of the class

Question 21.
The mean of the observations x – 1, x and x + 1 is
A) 3x
B) x
C) 2x
D) 0
Answer:
B) x

Question 22.
The median of first 10 natural numbers is
A) 11
B) 4.5
C) 6.5
D) 5.5
Answer:
D) 5.5

Question 23.
The classes 30 – 39, 40 – 49, 50 – 59, ……………… are called
A) Inclusive classes
B) Exclusive classes
C) Overlapping classes
D) Real classes
Answer:
A) Inclusive classes

Question 24.
The mode of the distribution 2, 5, 7, 5, 3, 1, 5, 8, 7, 5 is
A) 7
B) 6
C) 2
D) 4
Answer:
A) 7

Question 25.
The median value of the series 15, 12, 14, 20, 16, 10 is
A) 15
B) 14.5
C) 15
D) 14
Answer:
B) 14.5

Question 26.
The mid value of the class is used to calculate
A) Mode
B) Median
C) Arithmetic Mean
D) None of these
Answer:
C) Arithmetic Mean

Question 27.
Which of the following is not a measure of central tendency?
A) Range
B) Mean
C) Median
D) Mode
Answer:
A) Range

Question 28.
The mode of the observations 8,9,10, 11, 12, 8, 9, 12, 9, 8, 9,11, 9, 8 is
A) 8
B) 9
C) 10
D) 12
Answer:
B) 9

Question 29.
The median of the observations 6, 21, 9, 19, 15 and 13 is
A) 13
B) 19
C) 15
D) 14
Answer:
D) 14

Question 30.
The lower limit of the class 60 – 69 is
A) 9
B) 64.5
C) 60
D) 69
Answer:
C) 60

Question 31.
The upper limit of the class 30 – 40 is
A) 40
B) 30
C) 75
D) 10
Answer:
A) 40

Question 32.
The modal class of the following frequency distribution is

Class interval	Frequency
10 – 20	4
20 – 30	9
30 – 40	12
40 – 50	15
50 – 60	8
60 – 70	2

A) 30 – 40
B) 40 – 50
C) 50 – 60
D) 20- 30
Answer:
B) 40 – 50

Question 33.
The mean of first ten odd natural numbers is
A) 19
B) 10
C) 20
D) 5
Answer:
B) 10

Question 34.
The width of the class interval 40 – 50 is
A) 50
B) 45
C) 10
D) 40
Answer:
C) 10

Question 35.
The value of the observation which occurs most frequently is called
A) Mean
B) Median
C) Range
D) Mode
Answer:
D) Mode

Question 36.
The average weight of 5 packets is 24 kgs and the average weight of another 10 packets is 12 kgs, then average weight of 15 packets is ……………….
A) 6 Kgs
B) 16 Kgs
C) 10 Kgs
D) 36 Kgs
Answer:
B) 16 Kgs

Question 37.
Mode of the scores 7, 8, 5, 6, 3, 6, 7, 6, 1 is ………………….
A) 7
B) 5
C) 6, 7
D) 6
Answer:
C) 6, 7

Question 38.
12.5 is the class mark of the class interval
A) 10 – 15
B) 0 – 25
C) Both A and B
D) None
Answer:
B) 0 – 25

Question 39.
Mean of three consecutive even numbers is 16. The numbers are
A) -14,-16,-18
B) 13, 15, 17
C) -13, -15, -17
D) 14, 16, 18
Answer:
D) 14, 16, 18

Question 40.
10, 12, 12, 11, 8, 15 are the marks obtained by a group of IX class students in mathematics. Even though when two students Bhanu and Roja joined with them the median doesn’t changed. The possible marks of Bhanu and Roja are
A) 13, 18
B) 6, 9
C) 17, 18
D) 9, 18
Read the following information and answer the questions from 6 – 10.
Marks of students of a class were given

Answer:
D) 9, 18

Question 41.
From the given table the lower limit of highest frequency class
A) 30
B) 15
C) 20
D) 25
Answer:
C) 20

Question 42.
In the class no. of students more than 25 marks obtained is
A) 30
B) 5
C) 14
D) 25
Answer:
B) 5

Question 43.
If three students with marks 26, 27 and 28 were joined, which class frequency changes?
A) 30 – 35
B) 10 – 15
C) 20 – 25
D) 25 – 30
Answer:
D) 25 – 30

Question 44.
In the given data ‘ 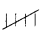’ represents
A) 20
B) 10
C) 15
D) 5
Answer:
D) 5

Question 45.
While drawing a bar graph, which class bar is the smallest in it’s length?
A) 15 – 20
B) 10 – 15
C) 25 – 30
D) 30 – 35
Answer:
D) 30 – 35

Question 46.
While writing the expansion form of 5161 we use some digits. Mode of the digits used in the expansion is
A) 0
B) 6
C) 5
D) 1
Answer:
C) 5

Question 47.
Given below are the marks obtained in a Mathematics examination of Class IX:

The above data was classified as 0 – 25, 25 – 50, 50 – 75, 75 – 100.
In which class the frequency is more?
A) 75 – 100
B) 0 – 25
C) 25 – 50
D) 50 – 75
Answer:
A) 75 – 100

Question 48.
In an ungrouped data there are 10 scores. After arranging them which term is the median?
A) Average of \(\frac{n^{\text {th }}}{2}\) term and
(\(\frac{n}{2}\) + 1)^th term
B) \(\frac{n^{\text {th }}}{2}\) term
C) (\(\frac{n}{2}\) + 1)^th term
D) (\(\frac{n+1}{2}\))^th term
Answer:

Question 49.
For an ungrouped data of 10 scores
Arithmetic mean is 12. If one more socre is joined to the previous scores the mean increases by 0.5 with this information.

Ravi: Ravi says that the new score will be 0.5 more than 12.
Harsha : Harsha says that the new score will be 5.5 more than 12.
Ritu : Ritu says that sum of 11 scores is 17.5 greater than sum of 10 scores. Now, which of these is correct?
A) All are correct.
B) Ravi and Harsha are correct.
C) Harsha and Ritu are correct.
D) Ravi and Ritu are correct.
Answer:
C) Harsha and Ritu are correct.

Question 50.
While doing a project work on weights of students in the class-room Sekhar found mean wt of the class as 28 kg, median as 29.5 kg and mode as 27 kg. While doing his project two students Eswar & Nawaz were absent in the class. If those two were attended mean, median and mode will not change. Then the possible wt’s of these two students are (in kgs)
A) 27, 29
B) 28, 28
C) 27.5, 28.5
D) 20, 36

Read the following and answer question 16 to 20 :
Data given of marks obtained by the students in an examination.

Marks obtained	No. of Students
Upto 5	5
Upto 10	11
Upto 15	19
Upto 20	25

Answer:
A) 27, 29

Question 51.
No. of students who got more than 15 marks:
A) 6
B) 25
C) 19
D) 11
Answer:
B) 25

Question 52.
If 6 students were failed, then the no. of students who passed and got up to 15 marks are
A) 13
B) 5
C) 6
D) 11
Answer:
A) 13

Question 53.
No. of students who are in the class of 10 – 15 is
A) 20
B) 6
C) 8
D) 14
Answer:
A) 20

Question 54.
If 5 more students are joined with marks 12,15,8,19,6 in the class, then the no. of students who got more than 15 marks are
A) 7
B) 10
C) 9
D) 8
Answer:
D) 8

Question 55.
In 10 – 15 class 10 is called as
A) Upper boundary of 10 – 15 class
B) Lower limit of 10 – 15 class
C) Upper limit of 10 – 15 class
D) Lower boundary of 10 – 15 class
Answer:
D) Lower boundary of 10 – 15 class

Question 56.
To find mean weight of 3 types of vegetables which are 4 kg, 6 kg, 8 kg, Usha and Laxmi do like these :
Usha : Weight given = 4 kg, 6 kg, 8 kg
Mean weight = \(\overline{\mathrm{X}}\) = \(\frac{3}{18}=\frac{1}{6}\) kg

Laxmi : Weight given = 4 kg, 6 kg, 8 kg
Mean weight = \(\overline{\mathrm{X}}\) = \(\frac{4 \times 6 \times 8}{3}\) = 64kg

From the above information
A) Both are wrong.
B) Usha only wrong.
C) Laxmi only wrong.
D) Both are right.
Answer:
A) Both are wrong.

Question 57.
A paper is folded several times. When it was opened it was observed that it contained 22 triangles and 22 quadrilaterals and 12 pentagons. From the above mode is
A) Both triangles and quadrilaterals
B) Triangles
C) Quadrilaterals
D) Pentagons
Answer:
B) Triangles

Question 58.
Means of first 10 whole numbers and first 10 natural numbers is in the ratio of
A) 9: 11
B) 10 : 11
C) 11 : 10
D) 11 : 9
Answer:
A) 9: 11

Question 59.
\(\overline{\mathrm{X}}\) = A + \(\frac{\mathbf{\Sigma f}_{\mathbf{i}} \mathbf{d}_{\mathbf{i}}}{\mathbf{\Sigma} \mathbf{f}_{\mathbf{i}}}\) is the formula to find
mean for an ungrouped data. In this formula letter A represents for
A) Assumed mean
B) Arithmetic mean
C) Frequency
D) Deviation value
Answer:
A) Assumed mean

Question 60.
Mean of first five even natural numbers is
A) 6
B) 8
C) 30
D) 10
Answer:
A) 6

Question 61.
Median of 10, 15, 7, x, 27, 30 is 16, then x =
A) 15
B) 17
C) 16
D) 18
Answer:
B) 17

Question 62.
Pulse rates per minute of a patient observed by the doctor are 72, 78, 90, 102 and 73. Then the average pulse rate is
A) 76
B) 79
C) 82
D) 83
Answer:
D) 83

Question 63.
In a cricket match an over contains six balls. In a T-20 Cricket match it was already 5 balls bowled in the last over. If Sachin hits six for the last ball the mean becomes 4 runs per ball in the over. But Sachin hits four runs. Then the mean score per ball in that over is
A) 3
B) 3\(\frac{2}{3}\)
C) 4
D) 6
3
Answer:
A) 3

Question 64.
The mid value of the class 10 – 19 is
A) 14
B) 14.5
C) 15
D) 15.5
Answer:
B) 14.5

Question 65.
For the given scores \(\overline{\mathrm{X}}\) = 12 and Σx₁ = 192, then n =
A) 12
B) 15.8
C) 16
D) 18
Answer:
C) 16

Question 66.
The mode of the scores 12, 11, 12, 9, 10, 9, 12 is
A) 9
B) 10
C) 11
D) 12
Answer:
D) 12

Question 67.
If the mean height of 3 boys is 142 cm. and the mean height of another 7 students is 145 cm., then the mean height of 10 students.
A) 144 cm
B) 144.1 cm
C) 144.2 cm
D) 144.4 cm
Answer:
B) 144.1 cm

Question 68.
The median of rational numbers \frac{1}{2}, \frac{2}{3}, \frac{5}{6}, \frac{1}{4} and \(\frac{3}{5}\)
A) \(\frac{1}{2}\)
B) \(\frac{3}{5}\)
C) \(\frac{2}{3}\)
D) \(\frac{5}{6}\)
Answer:
B) \(\frac{3}{5}\)

Question 69.
Mean of 2.5, \(\frac{5}{2}\), 5.2, \(\frac{2}{5}\) is ………………..
A) 0.4
B) 2.5
C) 2.65
D) 5.2
Answer:
C) 2.65

Question 70.
In the formula, \(\overline{\mathrm{X}}\) = \(\frac{\sum \mathbf{x}_{\mathbf{1}}}{\mathbf{n}}\) the letter \(\overline{\mathrm{X}}\) represents
A) No. of observations
B) Sum of observations
C) Product of observations
D) Mean of observations
Answer:
D) Mean of observations

Question 71.
a data is represented using the classes 20 – 29, 30 – 39, ………….., 120 – 129. What is the length of the class interval 90 – 99 ?
A) 90
B) 89.5
C) 10
D) 9
Answer:
C) 10

Question 72.
Two students collected two different data sets P and Q for a project.
P :A table with the weights of all students of a class. The data was collected by a student for the project.
Q: A table with lists of daywise absentees in a class. The data was collected by using the class attendance register.
Which of the following is true about P and Q?
A) P is primary data & Q is primary data
B) P is secondary data & Q is primary data
C) P is primary data & Q is secondary data
D) P is secondary data & Q is secondary data
Answer:
C) P is primary data & Q is secondary data

Question 73.
For a data, the range is
A) Maximum Value – Minimum Value
B) Maximum Value + Minimum Value
C) Maximum Value × Minimum Value
D) Maximum Value / Minimum Value
Answer:
A) Maximum Value – Minimum Value

Question 74.
A data of n observations (n is odd number) is arranged in descending order, then which observation represents median?
A) [ (\(\frac{n}{2}\))^th + 1] observation
B) (\(\frac{n}{2}\))^th observation
C) [latex]\frac{n+1}{2}[/latex]^th observation
D) [latex]\frac{n-1}{2}[/latex]^th observation
Answer:
C) [latex]\frac{n+1}{2}[/latex]^th observation

Question 75.
For the data, 0, 1, – 1, 1, 2, which of the following is TRUE?
A) Mean = Median = Mode
B) Mean = Median ≠ Mode
C) Mean ≠ Median ≠ Mode
D) Mean ≠ Median = Mode
Answer:
C) Mean ≠ Median ≠ Mode

Question 76.
If each observation of the data 5, 6, 8, 10, 12, 14, 14, 15, 16, 20 is multiplied by 2, then median of new data is ……………….
A) 28
B) 26
C) 25
D) 24
Answer:
B) 26

Question 77.
Cumulative frequency is used in finding, which of the following?
A) Mean
B) Median
C) Mode
D) Range
Answer:
B) Median

Question 78.
Mode of the given data 6, 7, 8, 6, 7, 7, 9,8
A) 7
B) 8
C) 6
D) 9
Answer:
A) 7

Practice the AP 9th Class Maths Bits with Answers Chapter 10 Surface Areas and Volumes on a regular basis so that you can attempt exams with utmost confidence.

AP State Syllabus 9th Class Maths Bits 10th Lesson Surface Areas and Volumes with Answers

Choose the correct answer :

Question 1.
Surface area of a cuboid whose length, breadth and height are 10 cm, 8 cm and
8 cm is
A) 640 cm²
B) 224 cm²
C) 448 cm²
D) 288 cm²
Answer:
C) 448 cm²

Question 2.
Lateral surface area of a cube whose edge is 3.5 cm is
A) 12.25 cm²
B) 42.875 cm²
C) 73.5 cm²
D) 49 cm²
Answer:
D) 49 cm²

Question 3.
Volume of a right prism is
A) lbh
B) base perimeter × height
C) 2(lb + bh + lh)l + b + h
D) none
Answer:
A) lbh

Question 4.
The volume of a cuboid whose side 8 cm is
A) 144 cm³
B) 216 cm³
C) 512 cm³
D) 384 cm³
Answer:
C) 512 cm³

Question 5.
The volume of a pyramid is
A) \(\frac{1}{3}\) × Area of base × height
B) \(\frac{1}{2}\) × Area of base × height
C) Area of base × height
D) Perimeter of base × height
Answer:
A) \(\frac{1}{3}\) × Area of base × height

Question 6.
The volume of isosceles right angled triangular prism where the equal sides are 6 cm and 6 cm and height is 4 cm
A) 144 cm³
B) 48 cm³
C) 72 cm³
D) 60 cm³
Answer:
C) 72 cm³

Question 7.
The volume of a square pyramid whose base area is 16 cm and height 8 cm is
A) 128 cm³
B) 144 cm³
C) 64 cm³
D) 256 cm³
Answer:
A) 128 cm³

Question 8.
The volume of a cube is 729 cm³ ,then its side is
A) 27 cm
B) 9 cm
C) 7 cm
D) 36 cm
Answer:
B) 9 cm

Question 9.
The volume, length and breadth of a cuboid are 60 cm³, 5 cm, 4 cm then its height is
A) 3 cm
B) 4 cm
C) 5 cm
D) 1.5 cm
Answer:
A) 3 cm

Question 10.
If each dimension of a cuboid is increased by 4 times, then the total surface area becomes …………….. times the original area.
A) 4
B) 8
C) 12
D) 16
Answer:
D) 16

Question 11.
The base of a prism is a triangle with sides 5 cm, 12 cm, 13 cm the volume of the prism if its height is 6 cm
A) 180 cm³
B) 60 cm³
C) 360 cm³
D) can’t be determined
Answer:
A) 180 cm³

Question 12.
The C.S.A. of a right circular cylinder whose r = 21 cm and h = 7 cm
A) 924 cm²
B) 6468 cm²
C) 9702 cm
D) 67914 cm²
Answer:
A) 924 cm²

Question 13.
Total surface area of a cylinder whose diameter is 14 cm and height 7 cm
A) 1848 cm²
B) 1884 cm²
C) 1488 cm²
D) 392 cm²
Answer:
A) 1848 cm²

Question 14.
Volume of a cylinder when d = 7 cm and h = 3 cm
A) 118 cm³
B) 115.5 cm³
C) 155.5 cm³
D) 808.5 cm³
Answer:
B) 115.5 cm³

Question 15.
A rectangular piece of length 12 cm and breadth 4 cm is folded to form a cylinder. Find its curved surface area.
A) 16 cm²
B) 192 cm²
C) 48 cm²
D) 576 cm²
Answer:
C) 48 cm²

Question 16.
C.S.A of a cone is
A) \(\frac{1}{3}\)πr²h
B) πr²l
C) πrh
D) πrl
Answer:
D) πrl

Question 17.
The radius of the base and height of a cone are 5 cm and 12 cm then its slant height
A) 17 cm
B) 7 cm
C) 13 cm
D) 6 cm
Answer:
C) 13 cm

Question 18.
The C.S.A of a cone whose d = 7 cm, l = 4 cm
A) 34 cm²
B) 24 cm²
C) 54 cm²
D) 44 cm²
Answer:
D) 44 cm²

Question 19.
The T.S.A of a cone whose d = 14 cm, h = 24 cm
A) 504 cm²
B) 3696 cm²
C) 704 cm²
D) 528 cm²
Answer:
C) 704 cm²

Question 20.
Volume of a cone whose base radius is 4.2 cm and height is 4 cm
A) 73.92 cm²
B) 52.8 cm²
C) 48.6 cm²
D) 40.8 cm²
Answer:
A) 73.92 cm²

Question 21.
Surface area of a sphere is
A) 4πr²
B) 3πr²
C) 2πr²
D) 5πr²
Answer:
A) 4πr²

Question 22.
Volume of a sphere is
A) \(\frac{2}{3}\)πr³
B) \(\frac{4}{3}\)πr³
C) πr³
D) \(\frac{5}{6}\)πr³
Answer:
B) \(\frac{4}{3}\)πr³

Question 23.
Surface area of a hemisphere is
A) 2πr²
B) 3πr²
C) 4πr²
D) πr²
Answer:
B) 3πr²

Question 24.
The volume of a sphere whose radius is 7 cm
A) 1437.3 cm³
B) 4337 cm³
C) 2588 cm³
D) 4678 cm³
Answer:
A) 1437.3 cm³

Question 25.
The total surface area of a hemisphere whose radius is 14 cm
A) 2156 cm²
B) 616 cm²
C) 1258 cm²
D) 1848 cm²
Answer:
D) 1848 cm²

Question 26.
Which of the following is not a 3-D object?
A) Cone
B) Circle
C) Sphere
D) Cylinder
Answer:
B) Circle

Question 27.
Which of the following is a 3-D object?
A) Rectangle
B) Circle
C) Square
D) Cylinder
Answer:
D) Cylinder

Question 28.
The number of surfaces of a cuboid is
A) 4
B) 8
C) 6
D) 2
Answer:
C) 6

Question 29.
The lateral surface area of a cuboid with dimensions 12 cm × 9 cm × 5 cm is
A) 540 cm²
B) 210 cm²
C) 426 cm²
D) 213 cm²
Answer:
B) 210 cm²

Question 30.
The total length of all the edges of a cube of side 15 cm is
A) 225 cm
B) 120 cm
C) 180 cm
D) 60 cm
Answer:
C) 180 cm

Question 31.
The edge of a cube whose volume is 1000 cm³
A) 10 cm
B) 100 cm
C) 50 cm
D) 20 cm
Answer:
A) 10 cm

Question 32.
The lateral surface area of cube with side 8 cm is
A) 512 cm²
B) 64 cm²
C) 384 cm²
D) 256 cm²
Answer:
D) 256 cm²

Question 33.
Total surface area of a cylinder is
A) 2πr (r + h)
B) πrl
C) πr (l + r)
D) 2πrh
Answer:
A) 2πr (r + h)

Question 34.
Volume of a cone is
A) πr²h
B) \(\frac{1}{3}\)πr²h
C) πh (R² – r²)
D) 3πr²h
Answer:
B) \(\frac{1}{3}\)πr²h

Question 35.
A cone whose height and radius are 6 cm and 8 cm respectively. Then its
slant height is
A) 14 cm
B) 10 cm
C) 11 cm
D) 12 cm
Answer:
B) 10 cm

Question 36.
The radius and slant height of a cone are 8 cm and 17 cm respectively. Then its height is
A) 15 cm
B) 12 cm
C) 9 cm
D) 16 cm
Answer:
A) 15 cm

Question 37.
The height and slant height of a cone are 7 cm and 25 cm respectively. Then its radius is
A) 10 cm
B) 14 cm
C) 24 cm
D) 12.5 cm
Answer:
C) 24 cm

Question 38.
Volume of a hemisphere is
A) \(\frac{4}{3}\)πr³
B) \(\frac{2}{3}\)πr³
C) \(\frac{1}{3}\)πr²h
D) πr²h
Answer:
B) \(\frac{2}{3}\)πr³

Question 39.
The ratio of two spheres is 1 : 2, then the ratio of their surface areas is
A) 4 : 1
B) 1 : 8
C) 1 : 4
D) 8 : 1
Answer:
C) 1 : 4

Question 40.
The horizontal cross – section of a cyl-inder is a
A) circle
B) triangle
C) rectangle
D) isosceles triangle
Answer:
A) circle

Question 41.
The vertical cross – section of a cylinder is
A) square
B) rectangle
C) circle
D) sector
Answer:
B) rectangle

Question 42.
The vertical cross – section of a cone is
A) triangle
B) circle
C) isosceles triangle
D) right angled triangle
Answer:
C) isosceles triangle

Question 43.
When a cone is opened along its slant height, it gets the shape of a
A) sector
B) rectangle
C) square
D) equilateral triangle
Answer:
A) sector

Question 44.
When a cylinder is opened along its height, it gets the shape of a
A) square
B) circle
C) rectangle
D) sphere
Answer:
C) rectangle

Question 45.
Area of an equilateral triangle whose side is 2 cm is
A) 2√3 cm²
B) √3 cm²
C) 4 cm²
D) 8 cm²
Answer:
B) √3 cm²

Question 46.
Volume of a pyramid whose base area is 18 cm² and height 8 cm is
A) 48 cm³
B) 64 cm³
C) 72 cm³
D) 96 cm3
Answer:
A) 48 cm³

Question 47.
A regular square pyramid has its base edge 6 cm and height 5 cm. Then its volume is
A) 36 cm³
B) 25 cm³
C) 11 cm³
D) 60 cm³
Answer:
D) 60 cm³

Question 48.
Volume of the cylinder formed by a sheet as shown in the given figure.

A) 220 cm³
B) 1540 cm³
C) 770 cm³
D) 440 cm³
Answer:
B) 1540 cm³

Question 49.
How does the total surface area of a box changed if each dimension is doubled?
A) T.S.A. of the box will become 4 times of original area.
B) T.S.A. of the box will become 3 times of original area.
C) T.S.A. of the box will become 6 times of original area.
D) T.S.A. of the box will become 8 times of original area.
Answer:
A) T.S.A. of the box will become 4 times of original area.

Question 50.
A rectangle of length 44 cm is folded along with its breadth and formed a cylinder. Then the radius of the cylinder (cms) is
A) 44
B) 22
C) 11
D) 7
Answer:
D) 7

Question 51.
Find curved surface area of a cylinder having r = x cm and h = y cm.
A) 2πx (x + y)
B) πx²y
C) πxy
D) 2πxy
Answer:
D) 2πxy

Question 52.
The ratio of volumes of cylinder and cone having same radii and heights is
A) 1 : 2
B) 1 : 3
C) 3 : 1
D) 2 : 1
Answer:
C) 3 : 1

Question 53.
Total surface area of the cylinder whose radius is 3.5 cm and height 2.1 cm.
A) 123.2 cm²
B) 46.2 cm²
C) 73.5 cm²
D) 7.35 cm²
Answer:
A) 123.2 cm²

Question 54.
Formula to find the slant height of a cone is
A) l = h² + r²
B) l² = h + r
C) l = \(\sqrt{h^{2}+r^{2}}\)
D) l = h + r
Answer:
C) l = \(\sqrt{h^{2}+r^{2}}\)

Question 55.
Surface area of a sphere whose radius is 1 unit.
A) 2π
B) 4π
C) 4πr²
D) 2πr²
Answer:
B) 4π

Question 56.
A cone and cylinder have equal bases and heights. Their volumes in the ratio of
A) 1 : 3
B) 3 : 1
C) 2 : 3
D) 3 : 2
Answer:
A) 1 : 3

Question 57.
The total surface area of cube is 96 cm², then it’s volume is
A) 8 cm³
B) 27 cm³
C) 64 cm³
D) 125 cm³
Answer:
C) 64 cm³

Question 58.
If the radius of sphere is 14 cm then it’s surface area is
A) 1464 cm²
B) 2464 cm²
C) 3464 cm²
D) 4464 cm²
Answer:
B) 2464 cm²

Question 59.
If the radius and height of a cylinder is x cm and y cm respectively, then the curved surface area of cylinder.
A) 2πx (x + y) cm²
B) 2π xy cm²
C) π x²y
D) 2π x²y cm²
Answer:
B) 2π xy cm²

Question 60.
The height of a cone is 12 cm. and its radius is 5 cm. then the slant height of cone is in cm.
A) 13
B) 17
C) 7
D) 12
Answer:
A) 13

Question 61.
If the radius of a cylinder doubled, keeping its lateral surface area the same then its height is……………….
A) Increased by 50%
B) Increased by 100%
C) Decreased by 50%
D) Decreased by 100%
Answer:
C) Decreased by 50%

Question 62.
Base of a coloured flag which is in the shape of triangle is 2 + √2 units and height is 2 – √2 units. Then the area of flag in square units.
A) 2
B) \(\frac{1}{2}\)
C) 1
D) 4
Answer:
C) 1

Question 63.
In a cylinder, if radius is halved and height is doubled, then volume will be
A) Doubled
B) Halved
C) Four times
D) Same
Answer:
B) Halved

Question 64.
The length of the longest flag pole that can be put in a store room of dimensions 10m × 10m × 5m is
A) 16m
B) 10m
C) 12m
D) 15m
Akshra playing with building blocks, which are of the shape of cubes, has built a structure as shown in given figure. If the edge of each cube is 3 cm, then answer the following questions from 10 to 14 :

Answer:
D) 15m

Question 65.
The volume of the structure built by Akshra
A) 305 cm³
B) 405 cm³
C) 505 cm³
D) 205 cm³
Answer:
B) 405 cm³

Question 66.
If Akshra formed a cuboid using all that cubes, then the total surface area of cuboid is
A) 177 cm²
B) 354 cm²
C) 405 cm²
D) 144 cm²
Answer:
C) 405 cm²

Question 67.
Minimum number of small cubes further more required to form a cube
A) 12
B) 36
C) 48
D) 8
Answer:
D) 8

Question 68.
If the ratio of volumes of two cubes is 8 : 27, then ratio of their total surface areas is
A) 2 : 3
B) 3 : 2
C) 3 : 1
D) 4 : 9
Answer:
D) 4 : 9

Question 69.
The radius of the sphere is 2x, then its volume will be
A) 4πx³
B) \(\frac{8 \pi}{3}\)x³
C) \(\frac{32}{3}\)πx³
D) \(\frac{4}{3}\)πx³
Answer:
C) \(\frac{32}{3}\)πx³

Question 70.
A pyramid is a three dimensional figure the base of which is
A) Only a square
B) Only a rectangle
C) Any polygon
D) Only a triangle
Answer:
B) Only a rectangle

Question 71.
The steps from solids to points are
A) solids – lines – surface – points
B) lines – points – surface – solids
C) lines – surface – points – solids
D) solids – surface – lines – points
Answer:
D) solids – surface – lines – points

Question 72.
A one side open cylindrical drum has inner radius 28 cm and height 2.1 m. then how much water store in the drum in litres?

(Hint : 1000 cubic cm = 1 litre)
A) 517.44
B) 51.744
C) 51744
D) 5174.40
Answer:
D) 5174.40

Question 73.
On a particular day, the rainfall recorded in a terrace of dimensions 6 m and 5 m is 15 cm. The quantity of water collected in terrace is
A) 450 litres
B) 3000 litres
C) 4500 litres
D) 300 litres
Answer:
A) 450 litres

Question 74.
The cost of construction of a wall 8 m long, 4 m height and 20 cm thick at the rate ₹ 25 per m³ is
A) ₹ 80
B) ₹ 160
C) ₹ 320
D) ₹ 16
Answer:
B) ₹ 160

Question 75.
Which of the following is the solid combination of cylinder and cone ?
A) Capsule
B) Ice cream
C) Rocket
D) Top
Answer:
C) Rocket

Question 76.
If the surface area of sphere is 154 cm², then its radius in cms.
A) 7
B) 14
C) 21
D) \(\frac{7}{2}\)
Answer:
B) 14

Question 77.
The total surface area of a cube is 96 cm², then its volume is
A) 27 cm³
B) 64 cm³
C) 512 cm³
D) 8 cm³
Answer:
B) 64 cm³

Question 78.
A hemispherical bowl has a radius of 3.5 cm, then its curved surface area is
A) 77 cm²
B) \(\frac{231}{2}\)cm²
C) \(\frac{539}{6}\)cm²
D) \(\frac{77}{2}\)cm²
Answer:
A) 77 cm²

Question 79.
If the surface area of sphere is 616 cm2, then its radius is
A) 3.5 cm
B) 7 cm
C) 14 cm
D) 21 cm
Answer:
B) 7 cm

Question 80.
In a cylinder, if radius is halved and height is doubled, then the volume will be
A) Same
B) Doubled
C) Halved
D) Four times
Answer:
C) Halved

Question 81.
Match the following group A to B. Choose correct.
Group – A
1) Volume of the Sphere
2) Volume of the cylinder
3) CSA of cone
4) Total surface area of Hemisphere

Group – B
a) 3πr²
b) πrl
c) \(\frac{4}{3}\)πr³
d) πr²h
A) 1 – a, 2 – b, 3 – d, 4 – c
B) 1 – b, 2 – c, 3 – a, 4 – d
C) 1 – c, 2 – d, 3 – b, 4 – a
D) 1 – d, 2 – a, 3 – c, 4 – b
Answer:
C) 1 – c, 2 – d, 3 – b, 4 – a

Question 82.
The cost of construction a wall whose dimensions are 8 m × 4 m × 20 cm at the rate of Rs. 25 per m³ is
A) Rs. 16
B) Rs. 80
C) Rs. 160
D) Rs. 320
Answer:
C) Rs. 160

Question 83.
If the area of the equilateral triangle is 8√3 cm², then its perimeter is in cms
A) 64
B) 32
C) 12√2
D) 4√2
Answer:
C) 12√2

Question 84.
Which of the following represents the flat surface area of hemisphere ?
A) πr²
B) 2πr²
C) 3πr²
D) 4πr²
Answer:
A) πr²

Question 85.
The curved surface area of a cylinder having r = x cm, h = y cm is ……… an
A) 2πr (x + y)
B) πx²y
C) πxy
D) 2πxy
Answer:
D) 2πxy

Question 86.
The ratio of volumes of cylinder and cone having same radii and heights
A) 1 : 3
B) 3 : 1
C) 1 : 2
D) 2 : 1
Answer:
B) 3 : 1

Question 87.
In a Rhombus the lengths of two diagonals are 10 cm and 13 cm then it’s area is……………………
A) 130 cm²
B) 65 cm²
C) 32.5 cm²
D) 46 cm²
Answer:
B) 65 cm²

Question 88.
In this figure Area of the parallelogram PQRS is…………………

A) PQ × SM
B) RS × KQ
C) PS × QN
D) All
Answer:
A) PQ × SM

Question 89.
A designer wanted to make a design with Iron rod. He has a rod of length 68 cm. He can do a rhombus of diagonals 16 cm, 30 cm and also a square. Which is a better option to cover more area with the given length?
A) Always both square & Rhombus
B) Square only
C) Rhombus only
D) Sometimes square and sometimes rhombus
D) Sometimes square and sometimes rhombus
Answer:
B) Square only

Question 90.
Area of the given figure is

A) 32 cm²
B) 12 cm²
C) 16 cm²
D) 28 cm²
Answer:
D) 28 cm²

Question 91.
≅ ABCD as shown in the figure is a field of a farmer. He sold ΔABX and ΔDCY to tally for ₹1.5 lakh in order to make it as a rectangular field AXYD. If he sells his total field, he might have get

A) ₹ 6 lakh
B) ₹ 1.5 lakh
C) ₹ 3 lakh
D) ₹ 45 lakh
Answer:
C) ₹ 3 lakh

Question 92.
A toy rocket is like a cone exactly mounted on a cylinder the vertical cross-section of the toy is
A) Hexagon
B) Parallelogram
C) Rhombus
D) Trapezium
Answer:
A) Hexagon

Question 93.
In a cyclic quadrilateral one set of opposite angles are in the ratio of 2 : 3, then the angles are
A) 40° 60°
B) 60°, 90°
C) 90°, 135°
D) 72° , 108°
Answer:
D) 72° , 108°

Question 94.
From a metal sheet which is in the shape of a circle a biggest square with 10 cm as side was taken. Then the radius of the circle is (in ems)
A) 5√2
B) 10√2
C) 5
D) 7.5
Answer:
B) 10√2

Question 95.
If the diagonal of a Rhombus are 12 cm. and 8.5 cm, then its area is
A) 51 cm²
B) 102 cm²
C) 56 cm²
D) 153 cm²
Answer:
A) 51 cm²

Question 96.
From a metal sheet which is in the shape of a circle a biggest square with 10 cm as side was taken. Then the radius of the circle is (in ems)
A) 5√2
B) 10√2
C) 5
D) 7.5
Answer:
B) 10√2

Practice the AP 9th Class Maths Bits with Answers Chapter 7 Triangles on a regular basis so that you can attempt exams with utmost confidence.

AP State Syllabus 9th Class Maths Bits 7th Lesson Triangles with Answers

Choose the correct answer :

Question 1.
Figures having same shape and size are called …………… figures.
A) congruent
B) identical
C) similar
D) different
Answer:
A) congruent

Question 2.
Two squares are congruent if they have same
A) shape
B) side
C) angles
D) none
Answer:
B) side

Question 3.
If ∆PQR = ∆ABC then ∠R =
A) ∠A
B) ∠B
C) ∠C
D) right angle
Answer:
C) ∠C

Question 4.
Any two circles are
A) similar
B) congruent
C) equal
D) not equal
Answer:
A) similar

Question 5.
In the figure ΔABC = ΔCDA by

A) S.A.S.
B) R.H.S.
C) A.S.A.
D) S.S.S. B
Answer:
D) S.S.S. B

Question 6.
In the figure PQ = RS; bisect at ‘O’ then ΔPOR ≅ ΔQOS by

A) A.S.A
B) S.S.S
C) A.A.S.
D) S.A.S.
Answer:
D) S.A.S.

Question 7.
APQR is an isosceles triangle and ‘S’ is the mid-point of \(\overline{\mathrm{QR}}\), then ∆PQS =

A) ∆PSR
B) ∆RSP
C) ∆SPR
D) ∆PRS
Answer:
D) ∆PRS

Question 8.
\(\overline{\mathrm{XY}}\) is the perpendicular bisector of \(\overline{\mathrm{PQ}}\). Then ∆POX = ∆QOX by

A) S.A.S
B) A.S.A
C) S.S.S
D) A.A.A.
Answer:
A) S.A.S

Question 9.
If in ∆DEF; DF is the longest side then the greatest angle is
A) ∠D
B) ∠E
C) ∠F
D) right angle
Answer:
B) ∠E

Question 10.
If in ∆PQR, PQ > QR then
A) ∠R < ∠P
B) ∠P > ZQ
C) ∠R > ∠P
D) ∠P < ∠Q
Answer:
C) ∠R > ∠P

Question 11.
In ∆ABC, which of the following is true ?
A) AB + BC < AC
B) AB – AC > AC
C) BC + CA < AB
D) AB + BC > AC
Answer:
D) AB + BC > AC

Question 12.
In ∆XYZ, W is a point on YZ such that XW = XZ then

A) XY = XW
B) XY > XW
C) XY < XW
D) XY < XZ
Answer:
B) XY > XW

Question 13.
In the figure AB is a line segment and PQ is an arc with centre A then

A) ∠QAB < ∠PAB
B) ∠QAB < ∠PAB
C) ∠QAB = ∠PAB
D) None
Answer:
A) ∠QAB < ∠PAB

Question 14.
In the figure PA = PB and QA = QB then ∠POA is angle.

A) Acute
B) obtuse
C) right
D) reflex
Answer:
C) right

Question 15.
In rhombus ABCD, ∆AOB ≅

A) ∆BOC
B) ∆COD
C) ∆DOA
D) All of the above
Answer:
D) All of the above

Question 16.
In the figure PQ = SQ; PR = SR then ∆PQR ≅ ∆SQR by …………. congruence.

A) R.H.S.
B) S.A.S.
C) S.S.S.
D) A.S.A.
Answer:
C) S.S.S.

Question 17.
In ∆ABC, altitudes BD and CE are equal then ∆DCB ≅ ∆EBC by ………….. congruence

A) A.S.A.
B) S.A.S.
C) S.S.S.
D) R.H.S.
Answer:
D) R.H.S.

Question 18.
In ∆PQR, PQ = PR and RT and QU are medians then ∆QRT = ∆RQU by congruence.

A) R.H.S.
B) S.A.S.
C) A.S.A.
D) S.S.S.
Answer:
B) S.A.S.

Question 19.
∆ABC is isosceles with sides AB = AC; AD is the altitude, if ∠BAD = 50° then ∠CAD =
A) 40°
B) 130°
C) 50°
D) None
Answer:
C) 50°

Question 20.
If three angles of a triangle are equal to three angles of anothertriangle then they are
A) congruent
B) equal
C) similar
D) can’t be said
Answer:
A) congruent

Question 21.
From the given figures, we observe that

A) ∆ DEF ≈ ∆ ABC
B) ∆ EDF ≈ ∆ ABC
C) ∆ FDE ≈ ∆ ABC
D) None of the above
Answer:
C) ∆ FDE ≈ ∆ ABC

Question 22.
In the given figure AB and CD are in-tersecting at ‘O’. OA = OB, OP = OC, then

A) AD = BC
B) AD // BC
C) AB = CD
D) ∆ AOD ≈ ∆ COB
Answer:
B) AD // BC

Question 23.
In the given figure, AB // DC and AD // BC, then

A) ∆ ABC ≅ ∆ CDA
B) ∆ ABC ≅ ∆ DAC
C) ∆ ABC ≅ ∆ ADC
D) ∆ ABC ≅ ∆ ACD
Answer:
A) ∆ ABC ≅ ∆ CDA

Question 24.
In ∆ ABC, ∠BAD = ∠CAD and BD = DC, then

A) ∆ ABC is equilateral
B) ∆ ABC is scalene
C) ∆ ABC is isosceles
D) ∆ ABC is right angled
Answer:
C) A ABC is isosceles

Question 25.
The angle of an equilateral triangle is
A) 30°
B) 45°
C) 90°
D) 60°
Answer:
D) 60°

Question 26.
In ∆ ABC, AB = AC and AP ⊥ BC, we can prove that ∠B = ∠C using

A) SSS congruency rule
B) RHS congruency rule
C) SAS congruency rule
D) ASA congruency rule B
Answer:
B) RHS congruency rule

Question 27.
In AABC, AB > AC, then

A) ∠C < ∠B
B) AB + AC < BC
C) ∠C > ∠B
D) AB – AC > BC
Answer:
C) ∠C > ∠B

Question 28.
Which of the following set of measure-ments is not possible to construct a triangle ?
A) 5 cm, 8 cm, 4 cm
B) 5 cm, 4 cm, 3 cm
C) 7 cm, 5 cm, 3 cm
D) 5 cm, 8 cm, 1 cm
Answer:
D) 5 cm, 8 cm, 1 cm

Question 29.
Which measurement is required to make a triangle along with sides 4 cm and 6 cm ?
A) 1 cm
B) 2 cm
C) 3 cm
D) 1.5 cm
Answer:
C) 3 cm

Question 30.
Which of the following statement is not correct ?
A) In ΔABC, ∠A + ∠B + ∠C = 180°
B) In ΔABC, if AB > BC, then C > A
C) In a right angled triangle, the hypot-enuse is the smallest side
D) In ΔABC, if AB = BC, then ∠C = ∠B
Answer:
C) In a right angled triangle, the hypot-enuse is the smallest side

Question 31.
Which congruency rule is applied in the following figures ?

A) R.H.S.
B) A.S.A.
C) SAS.
D) S.S.S
Answer:
C) SAS.

Question 32.
Which congruency rule is apt for the following figures ?

A) S.S.S.
B) S.A.S.
C) A.S.A.
D) R.H.S.
Answer:
A) S.S.S.

Question 33.
Which congruency rule is followed in the following figures ?

A) S.A.S.
B) A.S.A.
C) R.H.S.
D) S.S.S.
Answer:
B) A.S.A.

Question 34.
Which congruency rule is taken into consideration in the following figures ?

A) S.S.S
B) S.A.S
C) A.S.A
D) R.H.S
Answer:
D) R.H.S

Question 35.
In ΔPQR, PQ = 5 cm, QR = 12 cm and PR = 13 cm, then PQR is
A) an acute angled triangle
B) a right angled triangle
C) an obtuse angled triangle
D) an equilateral triangle
Answer:
B) a right angled triangle

Question 1.
Among the following a true statement in ΔABC is
A) \(\overline{\mathrm{AB}}+\overline{\mathrm{BC}}<\overline{\mathrm{AC}}\)
B) \(\overline{\mathrm{BC}}+\overline{\mathrm{CA}}<\overline{\mathrm{AB}}\) C) \(\overline{\mathrm{AC}}+\overline{\mathrm{AB}}>\overline{\mathrm{BC}}\)
D) \(\overline{\mathrm{AB}}+\overline{\mathrm{BC}}=\overline{\mathrm{AC}}\)
Answer:
C) \(\overline{\mathrm{AC}}+\overline{\mathrm{AB}}>\overline{\mathrm{BC}}\)

Question 2.
In ΔABC, AB = 8 cm, BC = 5 cm, CA = 9 cm then the greatest angle is
A) ∠A
B) ∠B
C) ∠C
D) ∠B, ∠C
Answer:
B) ∠B

Question 3.
In ΔABC, BC = 10 cm, CA = 15 cm then the measure of AB is
A) Less than 25 cm
B) Greater than 25 cm
C) Equal to 25 cm
D) Less than 5 cm
Answer:
B) Greater than 25 cm

Question 4.
In which figure represents Δ ABC ≅ Δ XYZ w.r.t. to the A.S.A. rule ?

Answer:
C

Question 5.
In ΔXYZ, if ∠X = 40°, ∠Y = 60°, ∠Z = 80° then the smallest side is …………….
A) \(\overline{X Y}\)
B) \(\overline{Y Z}\)
C) \(\overline{Y Z}\)
D) both B and C
Answer:
B) \(\overline{Y Z}\)

Question 6.
In Δ ABC, AB = AC and an exterior angle ∠ACD = 105° then ∠BAC – ?
A) 105°
B) 60°
C) 30°
D) 75°
Answer:
C) 30°

Question 7.
In a Δ ABC, AD and BE are medians of Δ ABC and BE || DF, then the ratio of CF : AC

A) 1 : 3
B) 3 : 1
C) 4 : 1
D) 1 : 4
Answer:
D) 1 : 4

Question 8.
In Two right angle triangles their hy-potenuse AB, EF are equal and AC = DE then which is true statement of the following ?
A) ΔABC ≅ ΔDEF
B) ΔABC ≅ ΔEFD
C) ΔACB ≅ ΔEDF
D) Both B and C
Answer:
D) Both B and C

Question 9.
Three angles of a Triangle are in the ratio 2:3:5 then the angles are
A) 30°, 60°, 90°
B) 36°, 54°, 90°
C) 40°, 50°, 90°
D) 40°, 60°, 80°
Answer:
B) 36°, 54°, 90°

Question 10.
The angles of a triangle are in the ra-tio 5 : 3 : 7 then, the triangle is
A) An obtuse angled triangle
B) Right angle triangle
C) An Isosceles triangle
D) An acute angled triangle
Answer:
D) An acute angled triangle

Question 11.
From the adjacent figure, the value of x + y is

A) 110°
B) 140°
C) 170°
D) 30°
Answer:
A) 110°

Question 12.
In ΔABC, ∠A = 40°. If \(\overrightarrow{\mathbf{B O}}\) and \(\overrightarrow{\mathbf{C O}}\) are the bisectors of ZB and ZC, then the value of ∠BOC is

A) 110°
B) 70°
C) 40°
D) 140°
Answer:
A) 110°

Question 13.
If one angle of a triangle is equal to the sum of the other two angles, then the triangle is
A) An isosceles triangle
B) An obtuse triangle
C) An equilateral triangle
D) A right triangle
Answer:
C) An equilateral triangle

Question 14.
The ratio of angles in a triangle is 1:2:3 then the triangle is
A) Equilateral
B) Isosceles
C) Obtuse angled
D) Right angled
Answer:
D) Right angled

Question 15.
Which is not Pythagorean triplet in the following
A) (3, 4, 5)
B) (1, 2, 3)
C) (6, 8, 10)
D) (5, 12, 13)
Answer:
B) (1, 2, 3)

Question 16.
From the given figure area of ΔABC is

A) \(\frac { 1 }{ 2 }\) x AC x BC
B) \(\frac { 1 }{ 2 }\) x AB x BC
C) \(\frac { 1 }{ 2 }\) x AB x AC
D) \(\frac { 1 }{ 2 }\) x AB x BC x AC
Answer:
C) \(\frac { 1 }{ 2 }\) x AB x AC

Question 17.
Which of these is a postulate ?
A) A.A.A.
B) A.S.A.
C) S.S.S.
D) S.A.S.
Answer:
A) A.A.A.

Question 18.
In the given diagram BD = AD and AC = CD, then ∠CAB : ∠ABD

A) 3 : 1
B) 1 : 3
C) 1 : 4
D) 4 : 1
Answer:
A) 3 : 1

Question 19.
In ΔABC, D, E are the mid points of \(\overline{\mathbf{A}} \overline{\mathbf{B}}, \overline{\mathbf{A C}}\) . F, G are the mid-points of \(\overline{\mathrm{AD}}, \overline{\mathrm{AE}}\) . If \(\overline{\mathbf{F G}}\) = 2 cm, then BC =
A) 10 cm
B) 4 cm
C) 6 cm
D) 8 cm
Answer:
D) 8 cm

Question 20.
ΔPQR is an equilateral triangle. X, Y, Z are the mid-points of the sides and A, B, C are the mid-points of sides of ΔXYZ. If the perimeter of ΔPQR is 8.4 cm, then the perimeter of ΔABC =
A) 4.2 cm
B) 8.4 cm
C) 2.1 cm
D) 2.8 cm
Answer:
D) 2.8 cm

Read the given data and answer the questions form 21 to 25.

Question 21.
From the data given, in APQR, PQ + PR = …………….cm.
A) 25
B) 19
C) 9.4
D) 10.4
Answer:
D) 10.4

Question 22.
The exterior angle at R in ΔPQR is
A) 120°
B) 60°
C) 80°
D) 100°
Answer:
C) 80°

Question 23.
Which are congruent in the given tri-angles?
A) None of these
B) ΔABC ≅ ΔXYZ
C) ΔXYZ ≅ ΔPQR
D) ΔABC ≅ ΔPQR
Answer:
D) ΔABC ≅ ΔPQR

Question 24.
In ΔXYZ the biggest angle is at which vertex ?
A) X + Y + Z
B) X
C) Y
D) Z
Answer:
B) X

Question 25.
ΔABC ≅ ΔPQR under which congru-ency criterion ?
A) A. A. A
B) S. S. S
C) S. A. S
D) A. S. A
Answer:
A) A. A. A

Question 26.
In the given triangle is it possible to exist all exterior angles as right angles.
A) Never possible
B) Always possible
C) Sometimes possible
D) There can be 2 rights angles
Answer:
D) There can be 2 rights angles

Question 27.
“In a triangle median divides the tri-angle into two triangles whose areas are equal.” Rough diagram for the above statement is

Answer:
B

Question 28.
From the given figure, what is the additional information needed to prove ΔOBE ≅ ΔOCD ?

A) BE = CD
B) ΔBOE = ΔCOD
C) ΔOBE = ΔOCD
D) BD = CE
Answer:
B) ΔBOE = ΔCOD

Question 29.
□ABCD is a Rhombus prove that the diagonals divide the rhombus into four congruent triangles, (let the point of intersection is O.) For the above problem what is R.T.P. ?
A) ΔABC ≅ ΔACD ≅ ΔABD ≅ ΔBCD
B) ΔABC ≅ ΔACD
C) ΔABD ≅ ΔBCD
D) ΔOAB ≅ ΔOBC ≅ ΔOCD ≅ ΔOAD
Answer:
D) AOAB ≅ AOBC ≅ AOCD ≅ AOAD

Question 30.
From the given figure, what is the ad-ditional information needed to prove ΔOBE ≅ ΔOCD ?

A) BE = CD
B) ∠BOE = ∠COD
C) ∠OBE = ∠OCD
D) BD = CE
Answer:
D) BD = CE

Question 31.
In ΔABC, \(\overline{\mathrm{AD}}, \overline{\mathrm{BE}}\) are medians \(\overline{\mathrm{BE}} \| \overline{\mathrm{DF}}\)
To prove CF = \(\frac { 1 }{ 4 }\) AC it was written as
In ΔABC ‘D’ is the mid-point of \(\overline{\mathrm{BC}}\) and BE || DF. As per triangle mid-point of \(\overline{\mathrm{CE}}\) .
CF = \(\frac { 1 }{ 2 }\) CE

Which of the following is the next step ?
A) CF = \(\frac { 1 }{ 2 }\)AC
B) 2CF = CE
C) CF = \(\frac { 1 }{ 2 }\) (\(\frac { 1 }{ 2 }\) AC)
D) 4CF = AC
Answer:
B) 2CF = CE

Question 32.
In ΔABC, ∠B = ∠C and if AB = x – 8, AC = 2x – 53, then x =
A) 45 units
B) 37 units
C) 29 units
D) 25 units
Answer:
A) 45 units

Question 33.
In triangle ABC, D is the mid-point of \(\overline{\mathrm{BC}}\) and \(\overline{\mathbf{A}} \overline{\mathbf{B}}=\overline{\mathbf{A C}}\) . If A and D are joined ΔABD ≅ ΔACD under the congruency rule.
A) A.S.A
B) S.A.S
C) A.A.A
D) S.S.S
Answer:
B) S.A.S

Question 34.
The circle which passes through all the three vertices of a triangle is
A) Incircle
B) Orthocircle
C) Circumcircle
D) Outercircle
Answer:
C) Circumcircle

Question 35.
The exterior angle of an equilateral triangle is
A) 30°
B) 60°
C) 90°
D) 120°
Answer:
D) 120°

Question 36.
Which one is not a congruency axiom of triangle ?
A) S.S.S.
B) S.A.S.
C) A.S.A
D) A.A.A
Answer:
D) A.A.A

Question 37.
Which congruency property is related to satisfy ΔABC ≅ ΔABD in the given figure

A) S. A. S
B) A.S.A
C) S.S.S
D) R.H.S
Answer:
A) S. A. S

Question 38.
The area of triangle of base 8 cm is 20 sq.cm then, length of the altitude of the triangle is ………..
A) \(\frac { 5 }{ 2 }\) cm
B) 5 cm
C) 80 cm
D) 160 cm
Answer:
B) 5 cm

Question 39.
If a, b and c are the lengths of sides of a triangle, which of the following is TRUE?
A) a + b>c, a-b>c
B) a + b < c, a-bc, a-b<c
D) a + b < c, a – b > c
Answer:
C) a + b>c, a-b ∠A > ∠C
C) ∠A < ∠B < ∠C
D) ∠B < ∠A < ∠C Answer: B) ∠B > ∠A > ∠C

Question 40.
If AB = QR, BC = PR and CA = PQ, then
A) ΔABC ≅ ΔPQR
B) ΔCBA ≅ ΔPRQ
C) ΔBAC ≅ ΔRPQ
D) ΔPQR ≅ ΔBCA
Answer:
B) ΔCBA ≅ ΔPRQ

Question 41.
What is the number of triangles that can be constructed with all positive integer sides if two sides are 3 cm, 3cm?
A) 3
B) 5
C) 6
D) 9
Answer:
B) 5

Question 42.
Number of independent measure-ments required to construct a triangle
A) 3
B) 2
C) 1
D) 0
Answer:
A) 3

Question 43.
Which of the following triangle con-gruency criteria is used to prove ΔABD ≅ ΔACD ?

A) SSS Congruency
B) SAS Congruency
C) ASA Congruency
D) RHS Congruency
Answer:
B) SAS Congruency

Question 44.
In triangle ABC, AB = 5 cm, BC = 4 cm, CA = 3 cm, which of the following is TRUE?
A) ∠A = ∠B = ∠C
B) ∠B > ∠A > ∠C
C) ∠A < ∠B < ∠C
D) ∠B < ∠A < ∠C Answer: B) ∠B > ∠A > ∠C

Question 45.
In a right triangle ABC, AB = AC, then which of the following is FALSE ?
A) (∠B + ∠C) > ∠A
B) ∠A > ∠B, ∠A > ZC
C) ∠A = ∠B + ∠C
D) ∠A = 2∠B = 2∠C
Answer:
C) ∠A = ∠B + ∠C

Practice the AP 9th Class Maths Bits with Answers Chapter 12 Circles on a regular basis so that you can attempt exams with utmost confidence.

AP State Syllabus 9th Class Maths Bits 12th Lesson Circles with Answers

Choose the correct answer :

Question 1.
The point which is at equidistant from the circumference of a circle is called
A) centre
B) incentre
C) radius
D) circumcentre
From the figure answer the following questions (2 and 3).

Answer:
A) centre

Question 2.
If ‘O’ is the centre of the circle then AB is
A) radius
B) diameter
C) semicircle
D) tangent
Answer:
B) diameter

Question 3.
If AC and AD are at equidistant from’O’ then
A) AC = CO
B) AD = DO
C) AC = AD
D) AO = AC
Answer:
C) AC = AD

Question 4.
Area enclosed by two radii and the arc between them is called
A) triangle
B) circle segment
C) sector
D) cyclic quadrilateral
Answer:
C) sector

Question 5.
Angle in the major segment of a circle is
A) Obtuse angle
B) Right angle
C) Straight angle
D) Acute angle
Answer:
D) Acute angle

Question 6.
Angle in the minor segment of a circle is
A) obtuse angle
B) zero angle
C) acute angle
D) right angle
Answer:
A) obtuse angle

Question 7.
A diameter divides the circle into two
A) unequal segments
B) equal segments
C) can’t say
D) none
Answer:
B) equal segments

Question 8.
Let ‘O’ be the centre of a circle. The distance of chord AB from O is greater than the distance of chord CD from ‘O’ then
A) AB = CD
B) AB > CD
C) AB < CD
D) Diameter = AB + CD
Answer:
B) AB > CD

Question 9.
In the figure, ‘O’ is the centre of the circle and A, AB = CD then ∠AOB =

A) ∠OAB
B) ∠OBC
C) ∠DOC
D) ∠OCD
Answer:
C) ∠DOC

Question 10.
In the above figure, if ∠AOB = ∠DOC
A) AB = DC
B) AB = OC
C) DC = OA
D) AB ≠ CD
Answer:
A) AB = DC

Question 11.
In the figure, the value of x is

A) 40°
B) 80°
C) 320°
D) 50°
Answer:
B) 80°

Question 12.
In the above figure, if ∠C = 60° then y =
A) 40°
B) 80°
C) 240°
D) 120°
Answer:
C) 240°

Question 13.
In the figure, ‘O’ is the centre of the circle, then

A) EF > CD > AB
B) EF = CD = AB
C) AB > CD > EF
D) None
Answer:
C) AB > CD > EF

Question 14.
In the figure, ∠AOB = ∠COD; AB = 3 cm then CD = …………………..

A) 1.5 cm
B) 6 cm
C) 3.5 cm
D) 3 cm
Answer:
D) 3 cm

Question 15.
In the figure, 0M AB and AM = 6 cm where ‘O’ is the centre of the circle then AB =

A) 6 cm
B) 12 cm
C) 3 cm
D) 6 √6 cm
Answer:
B) 12 cm

Question 16.
In the figure, ∠OMA =

A) 45°
B) 90°
C) 180°
D) None
Answer:
B) 90°

Question 17.
Number of points required to describe a circle is
A) one
B) two
C) three
D) infinite
Answer:
C) three

Question 18.
Number of circles that can be drawn through a given point is
A) 1
B) 2
C) 3
D) many
Answer:
D) many

Question 19.
Number of circles that can be drawn through two non-collinear points is
A) 2
B) 4
C) many
D) none
Answer:
C) many

Question 20.
Number of circles that can be drawn through three non-collinear points is
A) 4
B) 3
C) 2
D) 1
Answer:
D) 1

Question 21.
In the figure, ∠ADB =

A) 45°
B) 65°
C) 25°
D) 115°
Answer:
B) 65°

Question 22.
In the figure, ∠ABC is

A) 55°
B) 125°
C) 35°
D) cant be determined
Answer:
B) 125°

Question 23.
If a quadrilateral is cyclic then it is a
A) parallelogram
B) convex polygon
C) rhombus
D) rectangle
Answer:
D) rectangle

Question 24.
Angle subtended by an arc at its centre is ‘x°’ then, angle subtended by it at any other point on the circle is
A) \(\frac{\mathrm{x}^{\circ}}{2}\)
B) 2x°
C) x°
D) 180 – x°
Answer:
A) \(\frac{\mathrm{x}^{\circ}}{2}\)

Question 25.
The perpendicular from the centre of a circle to a chord
A) bisects it
B) equals to it
C) trisects it
D) none
Answer:
A) bisects it

Question 26.
The measure of the angle in a semicircle is
A) 90°
B) 180°
C) 60°
D) 45°
Answer:
A) 90°

Question 27.
Angles in the same segment are
A) unequal
B) cyclic
C) equal
D) complementary
Answer:
C) equal

Question 28.
The circle that passes through the vertices of a triangle is called its
A) In circle
B) Semi-circle
C) Quadrant
D) Circum circle
Answer:
D) Circum circle

Question 29.
If ABCD is a cyclic quadrilateral, then ∠A + ∠C =
A) 360°
B) 180°
C) 90°
D) 120°
Answer:
B) 180°

Question 30.
If the sum of the pairs of opposite angles of a quadrilateral is 180°, then the quadrilateral is
A) Cyclic
B) Symmetric
C) Eccentric
D) Genetic
Answer:
A) Cyclic

Question 31.
In the given figure, the value of x is

A) 55°
B) 90°
C) 70°
D) 60°
Answer:
C) 70°

Question 32.
In the given figure, ‘O’ is the centre of the circle, then the value of y is

A) 45°
B) 90°
C) 60°
D) 30°
Answer:
B) 90°

Question 33.
Which part of a circle divides it into two semicircles?
A) Radius
B) Diameter
C) Chord
D) Secant
Answer:
B) Diameter

Question 34.
Concentric circles have
A) Same centre and different radii
B) Same centre but different radii
C) Different radii but do not have the same centre.
D) Same radii but different centres
Answer:
A) Same centre and different radii

Question 35.
In the given figure, if ‘O’ is the centre of the circle, then the measure of x is

A) 70°
B) 25°
C) 40°
D) 35°
Answer:
D) 35°

Question 36.
The number of a non-coilinear points required to describe a circle is
A) 1
B) 2
C) 3
D) 4
Answer:
C) 3

Question 37.
A cyclic rhombus is a
A) Rectangle
B) Square
C) Parallelogram
D) Trapezium
Answer:
B) Square

Question 38.
A cyclic parallelogram is a
A) Square
B) Trapezium
C) Rectangle
D) Rhombus
Answer:
C) Rectangle

Question 39.
The angle subtended by a semi-circle at its centre is
A) 180°
B) 90°
C) 360°
D) 120°
Answer:
A) 180°

Question 40.
In the given figure, ‘O’ is the centre of the circle and OP ⊥ AB. If AP = 6 cm, then AB =

A) 3 cm
B) 9 cm
C) 12 cm
D) 18 cm
Answer:
C) 12 cm

Question 41.
How many circles can be drawn through three non-collinear points?
A) 1
B) 2
C) 3
D) None of these
Answer:
A) 1

Question 42.
In the given figure, arc AB = arc CD and if ∠AOB = 40°, then ∠COD =

A) 80°
B) 40°
C) 140°
D) 90°
Answer:
B) 40°

Question 43.
In the given figure, ‘O’ is the centre of the circle. If ∠ACB = 35°, then ∠AOB =

A) \(\frac{1}{2}\) ∠ACB
B) 3 ∠ACB
C) 55°
D) 2 ∠ACB
Answer:
D) 2 ∠ACB

Question 44.
In the given figure, x + y =

A) 185°
B) 175°
C) 150°
D) 160°
Answer:
B) 175°

Question 45.
In the given figure, ‘O’ is the centre of the circle and OP ⊥ AB. If OP = 6 cm and AP = 8 cm, then the radius of the circle is

A) 10 cm
B) 4 cm
C) 3 cm
D) 7 cm
Answer:
A) 10 cm

Question 46.
An angle subtended by the arc in a semi circle is at centre is
A) 90°
B) 120°
C) 360°
D) 180°
Answer:
A) 90°

Question 47.
If the length of the longest chord in a circle is 24 cins then it’s radius is ………………….
A) 12 cm
B) 24cm
C) 6 cm
D) 4 cm
Answer:
A) 12 cm

Question 48.
Two circles having radii 12 cm and 5 cm touches externally then the distance between the centres of two circles is……………….
A) 7 cm
B) 12 cm
C) 5 cm
D) 17 cm
Answer:
D) 17 cm

Question 49.
Let ‘O’ be the centre of circle and AB and CD’ are chords. The distance of chord AB from ‘O’ is longer than the distance of chord CD from ‘O’ then one of the following is true.
A) AB = CD
B) AB > CD
C) AB < CD D) AB + CD = 0
Answer:
B) AB > CD

Question 50.
Which of the following figure represents largest angle at centre subtended by a chord. (Note : Radii are equal).

Answer:
(D)

Question 51.
Given below are the lengths of chords of a circle. Among these one chord is passing through the centre. Identify the length of chord which is passing through the centre.
A) 7 cm
B) 7.5 cm
C) 8 cm
D) 6.5 cm
Answer:
C) 8 cm

Question 52.
In the given figure AC is the diameter. 0 is the centre of the semi-circle. B is a point on the semi circle.
If ∠C = 48° = then ∠OBA =

A) 48°
B) 42°
C) 90°
D) 32°
Answer:
B) 42°

Question 53.
In the given figure ∠CDE = 112°, then ∠AFE =
(Note : In a cyclic quadrilateral opposite angles are supplementary).

A) 112°
B) 68°
C) 78°
D) 168°
Answer:
B) 68°

Question 54.
In the given circle ‘O’ is the centre. ∠ABC + ∠AOC = 2 right angles. Then ∠AOD =

A) 120°
B) 60°
C) 90°
D) 180°
Answer:
B) 60°

Question 55.
The length of a chord that passes through the centre of a circle is 14 cm then what is the distance
A) 88 cm
B) 44 cm
C) 28 cm
D) 7 cm
Answer:
D) 7 cm

Question 56.
Angle In a semi circle is …………………
A) Zero angle
B) Right angle
C) Straight angle
D) Complete angle
Answer:
B) Right angle

Question 57.
Number of circles that can be drawn through three collinear points is ……………………
A) 0
B) 1
C) 3
D) Infinitely many
Answer:
A) 0

Question 58.
Which of the following is a FALSE statement?
A) Two line segments of same length are congruent.
B) Two circles of same radii are congruent.
C) Two angles of same measure are congruent.
D) Two triangles of same area are congruent
Answer:
D) Two triangles of same area are congruent

Practice the AP 9th Class Maths Bits with Answers Chapter 6 Linear Equation in Two Variables on a regular basis so that you can attempt exams with utmost confidence.

AP State Syllabus 9th Class Maths Bits 6th Lesson Linear Equation in Two Variables with Answers

Choose the correct answer :

Question 1.
An equation of the form ax + by + c = 0 is called a …………… equation.
A) linear
B) square
C) circular
D) rectangular
Answer:
A) linear

Question 2.
\(\frac{x}{3}+\frac{y}{4}=\frac{1}{24}\) in the form of ax + by + c = 0 is
A) 3x + 4y = 2
B) 4x + 3y = 2
C) 8x + 6y + 1 = 0
D) 8x + 6y – 1 = 0
Answer:
D) 8x + 6y – 1 = 0

Question 3.
The cost of a mango and a banana is 36, it can be expressed as
A) x – y = 36
B) x = 36 + y
C) x + y = 36
D) x + y + 36 = 0
Answer:
C) x + y = 36

Question 4.
The equation \(\sqrt{2} x=\sqrt{3} y+5\) in the form of ax + by + c = 0 is
A) \(\sqrt{2} x – \sqrt{3} y+5\)
B) \(\sqrt{2} x – \sqrt{3} y-5\)
C) \(\sqrt{2} x – \sqrt{3} y\) = 0
D) x – y – 5 = 0
Answer:
B) \(\sqrt{2} x – \sqrt{3} y-5\)

Question 5.
Comparing 5x – 6y = 10 with ax + by + c = 0, value of c is
A) 5
B) 6
C) 10
D) – 10
Answer:
D) – 10

Question 6.
Comparing 6x = 7y with linear equation, value of c is
A) 6
B) 7
C) 13
D) 0
Answer:
D) 0

Question 7.
Comparing x = \(\frac{7}{3}\) y with linear form, 3
A) 1
B) \(\frac{7}{3}\)
C) 3
D) 0
Answer:
C) 3

Question 8.
Comparing \(\frac{-\mathbf{x}}{8}=\frac{\mathbf{y}}{\mathbf{4}}\) with linear form,
A) \(\frac{-1}{2}\)
B) \(\frac{1}{8}\)
C) \(\frac{1}{4}\)
D) 2
Answer:
D) 2

Question 9.
\(\frac{8}{9}\) x = -y in linear form is
A) 8x + 9y = 0
B) 8x – 9y = 0
C) – 8x + 9y = 0
D) 8x – y = 9
Answer:
A) 8x + 9y = 0

Question 10.
“The sum of two numbers is 12″ in linear form
A) x – y = 12
B) x = 12
C) x = y + 12
D) x + y = 12
Answer:
D) x + y = 12

Question 11.
‘The difference between a number and twice the second number is 14’ in linear form
A) x + y = 14
B) x – y = 14
C) x + 2y=14
D) x – 2y – 14 = 0
Answer:
D) x – 2y – 14 = 0

Question 12.
‘Two angles x, y are supplementary”, in the linear form is
A) x + y – 90 = 0
B) x – y + 90 = 0
C) x + y – 180 = 0
D) x + y + 180 = 0
Answer:
C) x + y – 180 = 0

Question 13.
Any pair of values for which x and y satisfy the linear equation ax + by + c = 0 is called its
A) coefficients
B) solution
C) variable value
D) origin
Answer:
B) solution

Question 14.
If x = 2 then solution of 2x + 3y = 13 is
A) (2, 9)
B) (2, 3)
C) (3, 2)
D) (9, 2)
Answer:
B) (2, 3)

Question 15.
A linear equation has solutions.
A) one
B) two
C) three
D) many
Answer:
D) many

Question 16.
The number of solutions to 3x – 5y = 8 is
A) 1
B) 2
C) 4
D) many
Answer:
D) many

Question 17.
One solution to 5x + 3y – 22 = 0 is
A) (1,2)
B)(1, 1)
C) (2, 4)
D) (3, 4)
Answer:
C) (2, 4)

Question 18.
If x = 3 and y. = 3 is a solution of 2x – 3y – k = 0 then the value of k is
A) 3
B) – 3
C) 0
D) – 6
Answer:
B) – 3

Question 19.
If x = 0 and y = 1 is a solution of 5x – by + 3 = 0 then the value of b is
A) 1
B) 5
C) – 3
D) 3
Answer:
D) 3

Question 20.
The graph of a linear equation is a
A) straight line
B) circle
C) square
D) parabola
Answer:
A) straight line

Question 21.
The line of the form y = mx passes through is
A) (0, 0)
B) (2, 1)
C) (2, 2)
D) (0, 2)
Answer:
A) (0, 0)

Question 22.
Equation of a line parallel to X-axis is
A) x = 3
B) x = -5
C) y = 0
D) y = 3
Answer:
D) y = 3

Question 23.
Equation of a line parallel to Y-axis is
A) x = 8
B) x = 0
C) y = 0
D) y = – 5
Answer:
A) x = 8

Question 24.
If a point P lies on X-axis, then it may
A) (0,3)
B) (0, – 8)
C) (0, \(\frac { -1 }{ 2 }\) )
D) (5, 0)
Answer:
D) (5, 0)

Question 25.
Equation of X – axis is
A) x = 2
B) x = – 2
C) y = 0
D) y = 1
Answer:
C) y = 0

Question 26.
If (2, 2) is a solution of 3x + ay = 8, find ‘a’.
A) 2
B) 0
C) 6
D) 1
Answer:
D) 1

Question 27.
2015 x + 2016 y = 4031 represents a ………….
A) Straight line
B) Parabola
C) Curved line
D) Circle
Answer:
A) Straight line

Question 28.
From the equation 4x + y = 9, find ‘y’ if x = \(\frac { 9 }{ 4 }\)
A) 0
B) 9
C) 1
D) 2
Answer:
A) 0

Question 29.
The graph of x = k is a line parallel to Y – axis at a distance of k units and passing through the point
A) (0, k)
B) (0, 0)
C) (k, 0)
D) none of these
Answer:
C) (k, 0)

Question 30.
The graph of y = k is a line parallel to X – axis at a distance of k units and passing through the point
A) (k, 0)
B) (1, 1)
C) (0, 0)
D) (0, k)
Answer:
D) (0, k)

Question 31.
Equation of X – axis is
A) y – 1 = 0
B) y = 0
C) x = 0
D) x + y= l
Answer:
B) y = 0

Question 32.
Equation of Y – axis is
A) x – 1 = 0
B) x + y = 0
C) x = 0
D) y = 0
Answer:
C) x = 0

Question 33.
Which of the following points satisfy the equation x + 2y = 6 ?
A) (2,0)
B) (- 2, 0)
C) (0, 3)
D) (2, 3)
Answer:
C) (0, 3)

Question 34.
The point that does not lie on the line y = – x + 2 is
A) (- 1, – 1)
B) (2, 0)
C) (0, 2)
D) (- 1, 3)
Answer:
A) (- 1, – 1)

Question 35.
Write – 2x = \(\frac { -3 }{ 5 }\) y +1 in linear form
A) – 2x + 3y – 5 = 0
B) – 10x + 3y + 5 = 0
C) – 10x + 3y – 5 = 0
D) – 2x – 3y – 5 = 0
Answer:
C) – 10x + 3y – 5 = 0

Question 36.
Write 3x – 4y = 5 in the linear form
A) 3x – 4y – 5 = 0
B) 3x + 4y – 5 = 0
C) – 3x – 4y + 5 = 0
D) 3x + 4y + 5 = 0
Answer:
A) 3x – 4y – 5 = 0

Question 37.
The line which passes through the origin is
A) x + y = 3
B) y = 3x
C) x = 5
D) y = 4
Answer:
B) y = 3x

Question 38.
Which of the following is not a solution of 3x – y = 0 ?
A) (4, 12)
B) (6, 18)
C) (5, 15)
D) (- 3, 9)
Answer:
D) (- 3, 9)

Question 39.
The point which does not satisfy the equation x + y = 0 is mi i
A) (1,1)
B) (1, – 1)
C) (- 1, 1)
D)(-2,2)
Answer:
A) (1,1)

Question 40.
Given that x – 2y = 3. The value of ‘y’ in terms of ‘x’ is
A) \(\frac { x+3 }{ 2 }\)
B) \(\frac { x-3 }{ 2 }\)
C) \(\frac { -x+3 }{ 2 }\)
D) \(\frac { -x-3 }{ 2 }\)
Answer:
B) \(\frac { x-3 }{ 2 }\)

Question 41.
Which of the following is solution of the equation 2x – 5y = 10 ?
A) (0, 2)
B) (1/2, 2)
C) (3, – 1)
D) (0, – 2)
Answer:
D) (0, – 2)

Question 42.
Express the following statement as a linear equation in two variables. ‘The sum of two numbers is 24″.
A) x + 4y = 24
B) 4x + y = 24
C) x + y = 24
D) xy = 24
Answer:
C) x + y = 24

Question 43.
The equation \(\frac{x}{4}-\frac{y}{7}\) = 3 in linear form is
A) 4x – 7y – 84 = 0
B) 7x – 4y – 84 = 0
C) 4x + 7y – 84 = 0
D) 7x + 4y + 84 = 0
Answer:
B) 7x – 4y – 84 = 0

Question 44.
If (- 3, 2) is a solution of 5x – 8y + k = 0, then the value of k is
A) 15
B) 16
C) 31
D) 13
Answer:
C) 31

Question 45.
If (2, – 1) is a solution of 4x + by + 4 = 0, then the value of ‘b’ is
A) 12
B) 8
C) 4
D) – 12
Answer:
A) 12

Question 46.
A line parallel to X – axis is
A) y = – 3
B) x = 2
C) x + y = 5
D) y = 2x
Answer:
A) y = – 3

Question 47.
The number of solutions of 7x – 3y – 15 = 0 is
A) 2
B) 1
C) Infinite
D) 3
Answer:
C) Infinite

Question 48.
A line parallel to Y – axis is
A) x = 4
B) 2x – 3y + 1 = 0
C) y = 3
D) x = –\(\frac { 1 }{ 2 }\)y
Answer:
A) x = 4

Question 49.
The equation of a line parallel to X – axis and passing through (7, – 2) is
A) x = 7
B) y = -2
C) 7x + 2y = 0
D) 2x – 7y = 0
Answer:
B) y = -2

Question 50.
If x = 3, y = 2 is a solution of the equation 5x – 7y = k, then the value of ‘k’ is
A) 1
B) -11
C) 29
D) 31
Answer:
A) 1

Question 51.
If x = -3, y = -2 is a solution 5x – 7y = k, then the value of ‘k’
A) 0
B) 1
C) -1
D) 2
Answer:
C) -1

Question 52.
If x = 1, then the solution \(\frac{\mathbf{x}}{2}-\frac{\mathbf{y}}{\mathbf{3}}\) = 3 is
A) \(\left(1, \frac{-15}{2}\right)\)
B) \(\left(1, \frac{21}{2}\right)\)
C) \(\left(\frac{-15}{2}, 1\right)\)
D) \(\left(\frac{21}{2}, 1\right)\)
Answer:
A) \(\left(1, \frac{-15}{2}\right)\)

Question 53.
In this, which figure represents the y = -2?

Answer:
D)

Question 54.
If (\(\sqrt{5}\), – 3) is a solution of 75 x-V7y = k then the value of k is
A) 21
B) – 16
C) 16
D) 26
Answer:
D) 26

Question 55.
if the age of ‘x’ is 4 times of the age of ‘y’ then represent the information as a linear equation in two variables is….
A) x = 4y
B) y = 4x
C) y + 4x = 0
D) x + 4y = 0
Answer:
A) x = 4y

Question 56.
An auto charges Rs. 15/- for first kilometre and Rs. 8/- for each subsequent kilometre. If Prameela travelled 7 km., how much amount she would have paid ?
A) Rs. 105/-
B) Rs. 56/-
C) Rs. 71/-
D) Rs. 63/-
Answer:
D) Rs. 63/-

Question 57.
The distance of x = – 4 from the Y – axis is:…………..
A) 0 units
B) 1 unit
C) 4 units
D) – 4 units
Answer:
C) 4 units

Instructions : From the adjacent graph, answer the following questions (Q. No. 8-12) : In a school students prepared toilet cleaning acid by taking acid and water as shown in the graph. The quantity of acid taken and water are shown along X, Y axis respectively.

Question 58.
What is the scale factor used on X- axis?
A) 5 Units
B) 10 Units
C) 20 Units
D) 1 Unit
Answer:
C) 20 Units

Question 59.
Above given information represent as linear equation in two variables :
A) y = 3x
B) 3x = 4y
C) 4x = 3y
D) x = 3y
Answer:
A) y = 3x

Question 60.
If the quantity of acid is 20, then the quantity of water in units
A) 40
B) 20
C) 10
D) 60
Answer:
D) 60

Question 61.
In the diluted acid water quantity is 45, then the quantity of concentrated acid in units. [D]
A) 30
B) 90
C) 135
D) 15
Answer:
D) 15

Question 62.
What is the percentage of water in the diluted acid
A) 25
B) 33.3
C) 75
D) 20
Answer:
B) 33.3

Question 63.

Which of the following linear equations represent the co-ordinate points given in the table ?
A) 2y + 2 = x
B) 2x = y + 2
C) 2x – y = 2
D) 2x + 2 = y

Question 64.
The equation 2x + 5y = 7 has a unique solution, if x, y are
A) Positive real numbers
B) Real numbers
C) Rational numbers
D) Natural numbers
Answer:
D) Natural numbers

Question 65.
Statement (A) : A linear equation 2x + 3y = 5 has a unique solution.
Statement (B) : The line parallel to the Y-axis at a distance 4 units to the left of Y-axis is given by the equation x = -4.
Statement (C) : The graph of the equation y = mx + c passes through the origin. By the above statement which of the following are correct ?
A) B and C are true, A is false.
B) B and C are false, A is true.
C) B is true and A and C are false.
D) A and B are true. C is false.

Question 66.

Choose correct matching from column -1 to column – II.
A) i – Q, ii – S, iii – P
B) i – Q, ii – P, iii – R
C) i – Q, ii – P, iii – S
D) i – S, ii – R iii – P
Answer:
B) i – Q, ii – P, iii – R

Question 67.
The linear equation that converts Fahrenheit (F) to Celsius (C) is given by the relation C = \(\frac{\mathbf{5 F}-\mathbf{1 6 0}}{\mathbf{9}}\) What is the numerical value of temperature which is same in both the scale ?
A) 30°
B) -40°
C) 40°
D) -30°
Answer:
B) -40°

Question 68.
The autorikshaw fare in a city is charged ₹ 8 for the first kilometre and ₹ 4 per kilometre for subsequent dis-tance covered. If distance ‘x’ km and for charged ‘y\ then this information express as a linear equation in two variables is
A) y = 4 (x + 1)
B) y = 4x + 8
C) y = 4x – 8
D) y = 4(x – 1)
Answer:
B) y = 4x + 8

Question 69.
The graph of y = 6 is a line
A) Parallel to y-axis at a distance 6 units from the origin.
B) Making an intercept 6 on the x – axis.
C) Making an intercept 6 on both the axis.
D) Parallel to x – axis at a distance 6 units from the origin.
Answer:
D) Parallel to x – axis at a distance 6 units from the origin.

Question 70.
The point of the form (a, a) always lies on
A) y – axis
B) On the line y = x
C) On the line x + y = 0
D) x – axis
Answer:
B) On the line y = x

Question 71.
The graph of the linear equation 2x + 3y = 12 at what points cuts the X- axis and Y-axis ?
A) (0, 4), (6, 0)
B) (4, 0), (0, 6)
C) (0, 2), (3, 0)
D) (2, 0), (0, 3)
Answer:
A) (0, 4), (6, 0)

Question 72.
Which of the following graph represents the linear equation x + y = 0 ?

Answer:
B

Question 73.
Which of the following represent a line parallel to x-axis ?
A) 2x + y = 7-
B) 2y – 3 = y + 1
C) x + 3 = 0
D) x + y = 3
Answer:
B) 2y – 3 = y + 1

Question 74.
If (2,0) is a solution of the linear equa-tion 2x + 3y = K, then the value of K is
A) 4
B) 6
C) 5
D) 2
Answer:
A) 4

Question 75.
From the linear equation F = \(\frac { 9 }{ 5 }\) C + 32, the equal temperature (in Fahren Heat) to 30°C is
A) 63°
B) 68°
C) 72°
D) 86°
Answer:
D) 86°

Question 76.
The equation 2018x + 2019y = 0 represents a
A) Point
B) Line
C) Line segment
D) Circle
Answer:
B) Line

Practice the AP 9th Class Maths Bits with Answers Chapter 5 Co-Ordinate Geometry on a regular basis so that you can attempt exams with utmost confidence.

AP State Syllabus 9th Class Maths Bits 5th Lesson Co-Ordinate Geometry with Answers

Choose the correct answer :

Question 1.
To locate the exact position of a point, the number of references we need is
A) 0
B) 1
C) 2
D) 4
Answer:
C) 2

Question 2.
The point (- 2, 3) lies in ………….. quadrant.
A) IV
B) III
C) II
D) I
Answer:
C) II

Question 3.
The point (0, – 5) lies
A) on X-axis
B) on Y-axis
C) in Q₃
D) in Q₄
Answer:
B) on Y-axis

Question 4.
The distance of a point from Y-axis is called
A) y co-ordinate
B) 2nd co-ordinate
C) abscissa
D) origin
Answer:
C) abscissa

Question 5.
The distance of a point from X – axis is called …………
A) x co-ordinate
B)abscissa
C) first co-ordinate
D) ordinate
Answer:
D) ordinate

Question 6.
The mathematician who developed the study of co-ordinate geometry is
A) Euler
B) John Venn
C) Euclid
D) Rene Descartes
Answer:
D) Rene Descartes

Question 7.
In a co-ordinate system the horizon¬tal line is called
A) Y-axis
B) X-axis
C) Origin
D) Reference
Answer:
B) X-axis

Question 8.
The meeting point of the two axes in the co-ordinate plane is called
A) Origin
B) X-axis
C) Y-axis
D) (2, 3)
Answer:
A) Origin

Question 9.
A point on the X-axis is
A) (2, 3)
B) (3, 2)
C) (0, 2)
D) (8, 0)
Answer:
D) (8, 0)

Question 10.
A point on the Y-axis is
A) (4,-2)
B) (- 8, 3)
C)(4,4)
D) (0, 1)
Answer:
D) (0, 1)

Question 11.
In the co-ordinate plane the axes are ……………….. to each other.
A) parallel
B) perpendicular
C) neither parallel no perpendicular
D) none
Answer:
B) perpendicular

Question 12.
The co-ordinates of origin are
A) (1,1)
B) (- 1,1)
C) (1,0)
D) (0, 0)
Answer:
D) (0, 0)

Question 13.
The point (-2,-8) lies in
A) Q₁
B) Q₃
C) Q₂
D) Q₄
Answer:
B) Q₃

Question 14.
The point which is not on the X-axis is
A) (-1,0)
B) (8,0)
C) (2, 0)
D)(0,4)
Answer:
D)(0,4)

Question 15.
The point which is not on the Y-axis is
A) (-2,0)
B) (0, 2)
C) (0, – 3)
D) (0, 4)
Answer:
A) (-2,0)

Question 16.
The point which lies on both the axes is
A) (1,1)
B) (- 1, – 1)
C) (2, 2)
D) (0,0)
Answer:
D) (0,0)

Question 17.
X-axis is denoted by £§| t ]
A) y = 0
B) x = 0
C) x = y
D) none
Answer:
A) y = 0

Question 18.
Y-axis is denoted by
A) y = 0
B) x = 0
C) x = y
D) all the above
Answer:
B) x = 0

Question 19.
If the distance of a point from X-axis is 8 units and its distance from Y-axis is 3 units then the point is denoted by
A) (8,3)
B) (-8,3)
C) (- 3, 8)
D) (3, 8)
Answer:
D) (3, 8)

Question 20.
The x co-ordinate of a point is also called
A) ordinate
B) 2nd co-ordinate
C) abscissa
D) none
Answer:
C) abscissa

Question 21.
The mathematician who found an as-sociation between algebraic equations and geometric curves and figures is
A) Rene Descartes
B) Euclid
C) John Venn
D) Archimedes
Answer:
A) Rene Descartes

Question 22.
The y – co-ordinate of the point A (-4, -3) exceeds its x – co-ordinate by
A) – 1
B) – 7
C) 1
D) 7
Answer:
C) 1

Question 23.
The number of quadrants that the co-ordinate axes divide the cartesian plane into is
A) 1
B) 2
C) 3
D) 4
Answer:
D) 4

Question 24.
Which of the following points is at a distance of 6 units from Y – axis mea-sured along positive X – axis ?
A) (8, 6)
B) (6, 8)
C) (0, 6)
D) (8, 2)
Answer:
B) (6, 8)

Question 25.
The x – co-ordinate of (4, 5) is called
A) abscissa
B) ordinate
C) direction
D) 4
Answer:
A) abscissa

Question 26.
The y – coordinate of (6, – 8) is called
A) – 8
B) abscissa
C) ordinate
D) location
Answer:
C) ordinate

Question 27.
Which of the following is on \(\overline{\mathbf{O X}}\) in graph?
A) (1,0)
B) (0, 1)
C) (0, 0)
D) (0, – 1)
Answer:
A) (1,0)

Question 28.
If x > 0, y > 0, then (x, y) lies in
A) Q₃
B) Q₁
C) Q₄
D) Q₂
Answer:
B) Q₁

Question 29.
If x < 0, y < 0, then (x, y) lies in
A) Q₄
B) Q₂
C) Q₁
D) Q₃
Answer:
D) Q₃

Question 30.
If x > 0, y < 0, then (x, y) lies in
A) Q₂
B) Q₁
C) Q₄
D) Q₃
Answer:
C) Q₄

Question 31.
If x < 0, y < 0, then (x, y) lies in
A) Q₁
B) Q₂
C) Q₃
D) Q₄
Answer:
C) Q₃

Question 32.
The point with abscissa 3 and whose ordinate is less than its abscissa by 4, is
A) (3, 4)
B) (-3, 4)
C) (-1, 3)
D) (3,-1)
Answer:
D) (3,-1)

Question 33.
The point which lies in Q₄ is
A) (1, 2)
B) (- 1, – 2)
C) (1, – 2)
D)(-1, 2)
Answer:
C) (1, – 2)

Question 34.
Which of the following is on \(\overline{\mathbf{O Y}}\) graph?
A) (4,0)
B) (0, 0)
C) (- 3, 0)
D) (- 3, – 2)
Answer:
B) (0, 0)

Question 35.
Which of the following points abscissa is more than its ordinate by 2 ?
A) (- 4, 2)
B) (2, 4)
C) (- 1, 1)
D)(1,-1)
Answer:
D)(1,-1)

Question 36.
The figure formed with vertices (0,0), (1, 0), (1,1) and (0, 1) is called a m
A) rectangle
B) square
C) circle
D) none
Answer:
B) square

Question 37.
The point (- 2, 0) lies on
A) OX
B) OX’
C) OY
D) OY’
Answer:
B) OX’

Question 38.
The point (0, – 3) lies on
A) OX
B) OX’
C) OY
D) OY’
Answer:
D) OY’

Question 39.
The abscissa of the point (- 7, 2) is
A) -7
B) 2
C) 7
D) – 5
Answer:
A) -7

Question 40.
The ordinate of the point (4, – 6) is
A) 2
B) – 2
C) – 6
D) 2
Answer:
C) – 6

Question 41.
The abscissa and ordinate of a point are – 2 and – 4 respectively. Hence the co-ordinates of the point are[ ]
A) (2,-4)
B) (-2, 4)
C) (- 2, – 4)
D) (2, 4)
Answer:
C) (- 2, – 4)

Question 42.
Which of the following points lie on the axis?
A) (7, 0)
B) (4, – 2)
A) (- 2, – 3)
D) (- 1, 4)
Answer:
A) (7, 0)

Question 43.
The quadrant in which the point (5, – 3) lies is
A) Q₁
B) Q₂
C) Q₃
D) Q₄
Answer:
D) Q₄

Question 44.
The quadrant in which the point (-2,4) lies is
A) Q₄
B) Q₃
C) Q₂
D) Q₁
Answer:
C) Q₂

Question 45.
The point which lies in is Q₃ is
A) (- 7, 4)
B) (2, 0)
C) (0, 4)
D) (- 1, – 3)
Answer:
D) (- 1, – 3)

Question 46.
The number of references needed to locate the exact position a point in a plane is
A) 1
B) 2
C) 3
D) 4
Answer:
B) 2

Question 47.
The quadrant in which the point (- x, – y) lies where x < 0, y < 0 is
A) Q₁
B) Q₂
C) Q₃
D) Q₄
Answer:
A) Q₁

Question 48.
The point which lies on both the axes is
A) (2,-3)
B) (- 5, – 8)
C) (0, 0)
D) (- 1, 4)
Answer:
C) (0, 0)

Question 49.
The points (0, 0), (0, 3), (4, 3) and (4, 0) are plotted in graph sheet. The figured formed by joining the points with straight lines is
A) triangle
B) circle
C) square
D) rectangle
Answer:
D) rectangle

Question 50.
A (2, 5) and B (3, 7) are points in a graph sheet. The ordinate of B is more than that of A by
A) 1
B) 2
C) 3
D) 4
Answer:
B) 2

Question 51.
Among the following a line passing through origin is (x, y ≠ 0)
A) x + y = 6
B)\(\frac{x}{2}-\frac{y}{3}\) = 3
C) y = 3x
D) \(\sqrt{2}\)x + 3y = 9
Answer:
C) y = 3x

Question 52.
The equation of line parallel to X-axis
A) x = 0
B) y = k
C) x = k
D) x = 9
Answer:
B) y = k

Question 53.
Any point on the X-axis is of the form
A) (x, y)
B) (0, y)
C) (x, 0)
D) (x, x)
Answer:
C) (x, 0)

Question 54.
The point at a distance of 4 units from X-axis and 5 units from Y-axis is
A) (5, 4)
B) (4, 5)
C) (5, 6)
D) (4, 6)
Answer:
A) (5, 4)

Question 55.
If x > 0, y < 0 the point (x – y, y – x) lies in
A) Q₁
B) Q₂
C) Q₃
D) Q₄
Answer:
D) Q₄

Question 56.
In which of the following, the ordinate is twice of its abscissa ?
A) (-2, 4)
B) (4, 2)
C) (4, -2)
D) (2, 4)
Answer:
D) (2, 4)

Question 57.
If the point (x₁, y₁) lies in Q₂ and the
point (X₂, y₂) lies in Q₃ then (x₁ y₂) lies in
A) Q₄
B) Q₁
C) Q₂
D) Q₃
Answer:
D) Q₃

Read the information given below and answer the questions from 31 to 35. Ram plotted points like these :
A(0, – 4), B(0, 6), C(3, 4), D(3, – 4), E(3,7), F(7,3), G(- 3,4), H(6,0), I(- 6,0).

Question 58.
From the given information the point on positive Y-axis is
A) I
B) A
C) B
D) H
Answer:
C) B

Question 59.
The distance between C and D is
A) 6 units
B) 0 units
C) 4 units
D) 8 units
Answer:
D) 8 units

Question 60.
The point for which x-co-ordinate is greater than y by 4 is
A) D
B) C
C) E
D) F
Answer:
D) F

Question 61.
The distance from Y-axis to the point G is
A)-4
B) -3
C) 3
D) 4
Answer:
B) -3

Question 62.
If (x, y) = (7, 3), then (x + y, x – y) lies in
A) Q₄
B) Q₁
C) Q₂
D) Q₃
Answer:
B) Q₁

Question 63.
From the given following, point on Y-axis is
A) (-3,-%
B) (0, 0)
C) (2, 3)
D) (-3, 2)
Answer:
B) (0, 0)

Question 64.
One of the solution for the point where x co-ordinate > y co-ordinate
A) (-6,-3)
B) (-4, -5)
C) (4, 6)
D)(-3,2)
Answer:
B) (-4, -5)

Question 65.
The point in Q₂ which is at a distance of 6 units from X-axis, 3 units from Y- axis is
A) (3, 6)
B) (3, -6)
C) (-3, 6)
D)(-3,-6)
Answer:
A) (3, 6)

Question 66.
A (2, 4), B (2, 8), C (6, 8), D (6, 4) are the points in first quadrant. If AB, BC, CD and DA joined then □ABCD is
A) Rectangle
B) Trapezium
C) Parallelogram
D) Square
Answer:
A) Rectangle

Question 67.
If (x, y) is a point in fourth quadrant, that
A) x > 0, y < 0 B) x > 0, y > 0
C) x < 0, y < 0
D) x < 0, y > 0
Answer:
A) x > 0, y < 0

Question 68.
The area of triangle formed by the points (0, 0), (5, 0) and (0, 5) is
A) 5 sq. units
B) 7.5 sq. units
C) 10 sq. units
D) 12.5 sq. units
Answer:
D) 12.5 sq. units

Question 69.
The mathematician, who developed Co-ordinate Goemetry
A) Euclid
B) Ronald Fisher
C) Pythagorus
D) Rene Descartes
Answer:
D) Rene Descartes

Question 70.
The equation of X – axis is
A) y = 0
B) x = 0
C) y = x
D) x + y = 1
Answer:
A) y = 0

Question 71.
If x < 0 and y > 0 then (- x, y) belongs to which quadrant
A) Q₁
B) Q₂
C) Q₃
D) Q₄
Answer:
B) Q₂

Question 72.
Which of the points lie on Y – axis
A) (2, 0), (3, 0)
B) (1, 2), (2, 2)
C) (0, – 2), (0, 2)
D) (- 5, 3), (2, 3)
Answer:
C) (0, – 2), (0, 2)

Question 73.
The distance of the point (2, -3) from X-axis
A) 5 units
B) 3 units
C) 2 units
D) 1 unit
Answer:
B) 3 units

Question 74.
The distance between origin and die point (-3, 0)
A) 0 units
B) 3 units
C) 6 units
D) 9 units
Answer:
B) 3 units

Question 75.
x < 0, y < 0 then the point (x + y, -x -y) lies in the
A) First quadrant
B) Second quadrant
C) Third quadrant
D) Fourth quadrant
Answer:
C) Third quadrant

Question 76.
The equation of X – axis is ……………..
A) x = 0
B) y = 0
C) 1/x = 0
D) 1/y = 0
Answer:
B) y = 0

Question 77.
What is the distance of the point (-2,-3) from Y – axis ?
A) 3 units
B) 2 units
C) – 2 units
D) – 3 units
Answer:
B) 2 units

Question 78.
The distance between origin and the point (- 3, 0)
A) 6 units
B) 3 units
C) 0 units
D) – 3 units
Answer:
B) 3 units

Question 79.
Which point lies on the X – axis ?
A) (-2,0)
B) (0, – 4)
C) (- 3, – 4)
D) (5, 1)
Answer:
A) (-2,0)

Practice the AP 9th Class Maths Bits with Answers Chapter 11 Areas on a regular basis so that you can attempt exams with utmost confidence.

AP State Syllabus 9th Class Maths Bits 11th Lesson Areas with Answers

Question 1.
Area of a parallelogram is the product of its
A) consecutive sides
B) opposite sides
C) base and height
D) diagonals
Answer:
C) base and height

Question 2.
If a triangle and a parallelogram are
on the same base and between the same parallels then, area of the triangle is ……………. the area of parallelogram.
A) twice
B) equal
C) half
D) none
Answer:
C) half

Question 3.
If the areas of two triangles are equal then they are congruent.
A) True
B) False ,
C) Can’t say
D) None
Answer:
C) Can’t say

Question 4.
Area is expressed in
A) square units
B) cubic units
C) units
D) circular units
Answer:
A) square units

Question 5.
If a figure A is formed by two plane figures B and C then the area of A is
A) Area of B + Area of C
B) Area of B – Area of C
C) 2 (Area of B + Area of C)
D) \(\frac{1}{2}\) (Area of B + Area of C)
Answer:
A) Area of B + Area of C

Question 6.
The areas of two congruent figures are
A) unequal
B) equal
C) can’t say
D) none
Answer:
B) equal

Question 7.
If 1 cm represents 2.5 m then area of a square with 10 m is
A) 10 cm²
B) 4 cm²
C) 2.5 cm²
D) 1 cm²
Answer:
B) 4 cm²

Question 8.
In the figure, area of ΔABC =

A) 24 cm²
B) 48 cm²
C) 10 cm²
D) 12 cm²
Answer:
D) 12 cm²

Question 9.
In the above figure if D is the midpoint of AC then area of ABCD =
A) 24 cm²
B) 48 cm²
C) 12 cm²
D) 6 cm²
Answer:
D) 6 cm²

Question 10.
Area of the figure ABCDE is

A) 66 cm²
B) 24 cm²
C) 18²
D) 42²
Answer:
D) 42²

Question 11.
In the figure, ABCD is a parallelogram. Then the area of ΔAOD =

A) ΔAOB
B) ΔBOC
C) ΔDOC
D) All the above
Answer:
D) All the above

Question 12.
In the figure, AB // CF then □ABCD =

A) □ABED
B) □ABEF
C) □ABCF
D) □ABCE
Answer:
B) □ABEF

Question 13.
In the figure, area of □ABCD if the area of ΔADE is 24 cm²

A) 24 cm²
C) 48 cm²
B) 36 cm²
D) 12 cm²
Answer:
C) 48 cm²

Question 14.
In the figure, ABCD is a parallelogram with area 36 cm² then ar ΔADE + ΔBCE =

A) 18 cm²
B) 9 cm²
C) 72 cm²
D) 45 cm²
Answer:
A) 18 cm²

Question 15.
□ABCD is a parallelogram, then ΔAEH + ΔBEF + ΔCGF + ΔDGB is (where E, F, G and H are the mid points of the sides

A) □ABCD
B) □EFGH
C) \(\frac{1}{2}\) □EFGH
D) 2 □EFGH
Answer:
B) □EFGH

Question 16.
In the figure, ar ΔPQR = 15 cm² then ar ΔPQS =

A) 7.5 cm²
B) 15 cm²
C) 30 cm²
D) 10 cm²
Answer:
B) 15 cm²

Question 17.
In the above figure, ar ΔPTS =
A) ΔPQT
B) ΔQRT
C) 2ΔTSR
D) \(\frac{1}{2}\) ΔPQT
Answer:
B) ΔQRT

Question 18.
In ΔPQR, A, B and C are the mid points of the sides, then □AQRC =

A) \(\frac{1}{2}\) ΔPQR
B) \(\frac{1}{4}\) ΔPQR
C) \(\frac{3}{4}\) ΔPQR
D) \(\frac{2}{3}\) ΔPQR
Answer:
C) \(\frac{3}{4}\) ΔPQR

Question 19.
If □PQRS = 30 cm² then PM =

A) 6 cm
B) 3 cm
C) 20 cm
D) None
Answer:
B) 3 cm

Question 20.
A polygon can be divided into …………………… regions.
A) Square
B) Rectangular
C) Circular
D) Triangular
Answer:
D) Triangular

Question 21.
ΔABC and parallelogram ABCD are on the same base AB and in between the parallel lines AB and EF. If ar (ΔABC) = 12.5 cm², then area of parallelogram ABCD =
A) 6.25 cm²
B) 25 cm²
C) 12.5 cm²
D) 10 cm²
Answer:
B) 25 cm²

Question 22.
E, F, G and H are respectively the mid points of the sides AB, BC, CD and AD of a parallelogram ABCD. If ar (ABCD) = 24 cm², then ar (EFGH) =

A) 12 cm²
B) 48 cm²
C) 36 cm²
D) none of these
Answer:
A) 12 cm²

Question 23.
In ΔABC, if ar (ΔABD) = ar (ΔACD), then AD is

A) an altitude
B) a diagonal
C) a median
D) the base
Answer:
C) a median

Question 24.
In the given figure, ΔABC, D, E, F are the mid points of sides BC, CA and AB
respectively. Then BDEF is a

A) square
B) rectangle
C) rhombus
D) parallelogram
Answer:
D) parallelogram

Question 25.
In ΔABC, E is the mid point of median AD. If ar (ΔABE) = 4.5 cm², then ar
(ΔABC) =

A) 9 cm²
B) 13.5 cm²
C) 18 cm²
D) 27 cm²
Answer:
C) 18 cm²

Question 26.
Area of a parallelogram is
A) base × altitude
B) \(\frac{1}{2}\) × base × height
C) Product of the diagonals
D) Half of the product of the diagonals
Answer:
A) base × altitude

Question 27.
Area of a Rhombus is
A) \(\frac{1}{2}\) × base x height
B) Product of the diagonals
C) Half of the product of the diagonals
D) \(\frac{1}{2}\) × sum of the parallel sides × distance between them
Answer:
C) Half of the product of the diagonals

Question 28.
Area of a parallelogram is 64 cm² with base 16 cm. Then its height is
A) 8 cm
B) 4 cm
C) 6 cm
D) 5 cm
Answer:
B) 4 cm

Question 29.
Area of the trapezium shown in the given figure is

A) (p + q)d
B) \(\frac{1}{2}\) pq
C) \(\frac{\mathrm{p}+\mathrm{q}}{\mathrm{d}}\)
D) \(\frac{1}{2}\) d(p + q)
Answer:
D) \(\frac{1}{2}\) d(p + q)

Question 30.
Area of Rhombus ABCD is 27 cm², if the diagonal BD is 6 cm, then the length of other diagonal AC is
A) 4.5 cm
B) 9 cm
C) 3 cm
D) 12 cm
Answer:
B) 9 cm

Question 31.
If parallelogram ABCD = 72 cm², then parallelogram ABEF =

A) 72 cm²
B) 36 cm²
C) 48 cm²
D) 60 cm²
Answer:
A) 72 cm²

Question 32.
ABCD is a parallelogram. The diagonals AC and BD intersect at ‘O’. If ar (ΔAOB) = 3.5 cm², then ar (ΔABC) =

A) 10.5 cm²
B) 21 cm²
C) 7 cm²
D) 14 cm²
Answer:
C) 7 cm²

Question 33.
In the given figure, D, E are points on the sides AB and AC respectively of ΔABC. Also ar (ΔDBC) = ar (ΔEBC), then

A) ar (ΔADE) = \(\frac{1}{2}\)ar (ΔDBC)
B) ar (ΔADE) = \(\frac{1}{2}\)ar (ΔEBC)
C) ar (ΔABE) = ar (ΔACD)
D) DE // BC
Answer:
D) DE // BC

Question 34.
Area of a rhombus with diagonals 6 cm and 10 cm is
A) 60 cm²
B) 30 cm²
C) 16 cm²
D) 15 cm²
Answer:
B) 30 cm²

Question 35.
ABCD is a trapezium in which AB // CD. If AB = 6.5 cm, CD = 3.5 cm and DE = 2 cm, then its area is

A) 13 cm²
B) 7 cm²
C) 20 cm²
D) 10 cm²
Answer:
D) 10 cm²

Question 36.
In the adjacent figure the ratio of ar (ΔAPB) and ar (ΔDQC) is ……………….

A) 1 : 2
B) 2 : 1
C) 1 : 1
D) 1 : 3
Answer:
C) 1 : 1

Question 37.
Sum of the exterior angles of an equilateral triangle
A) 360°
B) 180°
C) 120°
D) 90°
Answer:
A) 360°

Question 38.
In this figure ∠x + ∠y = ……………….

A) 80°
B) 260°
C) 180°
D) 160°
Answer:
B) 260°

Question 39.
In the given figure AC = 5.4 cm, BD = 5.8 cm and AD = 8.4 cm, BC = ………………

A) 2.6 cm
B) 2.8 cm
C) 3.0 cm
D) 3.2 cm
Answer:
B) 2.8 cm

Question 40.
The probability that a randomly thrown dart hits the square board in shaded region =

A) \(\frac{1}{4}\)
B) \(\frac{1}{2}\)
C) \(\frac{3}{4}\)
D) 1
Answer:
B) \(\frac{1}{2}\)

Question 41.
In the given diagram □ ABCD is the parallelogram with sides 3 cm and 2 cm, □ BEFP is also a parallelogram with sides 6 cm. and 1 cm. □ BQGH is another parallelogram with 4 cm. and 1.5 cm.

Which of these is more in area?
A) All are equal in areas.
B) □ ABCD
C) □ BEFP
D) □ BQGH
Answer:
A) All are equal in areas.

Question 42.
In any ΔABC, D is a point on BC such that ar (ΔABD) = ar (ΔADC then \(\overline{\mathrm{AD}}\) represents.
A) Altitude
B) Median
C) Angle bisector
D) Perpendicular Bisector
Answer:
B) Median

Question 43.
Which of the following pair of triangles have the same base and lie between the same parallels in the given figure

A) ΔAOB and ΔCOD
B) ΔAOD and ΔBOC
C) ΔABC and ΔABD
D) ΔABC and ΔADC
Answer:
C) ΔABC and ΔABD

Question 44.
In the following figure, DE = 7 cm, BC = ……………….

A) 3.5 cm
B) 7 cm
C) 14 cm
D) 49 cm
Answer:
C) 14 cm