Practice the AP 10th Class Maths Bits with Answers Chapter 7 Coordinate Geometry on a regular basis so that you can attempt exams with utmost confidence.
AP State Syllabus 10th Class Maths Bits 7th Lesson Coordinate Geometry with Answers
Question 1.
Write the nearest point to origin,
i) (2, – 3)
ii) (5, 0)
iii) (0, – 5)
iv) (1, 3)
Answer:
(1,3)
Question 2.
The distance of a point (3, 4) from the origin is how many units ?
Answer:
5 units.
Question 3.
Write the formula to find the area of a triangle.
Answer:
Δ = \(\frac { 1 }{ 2 }\) bh and
Δ = \(\sqrt{s(s-a)(s-b)(s-c)}\)
Question 4.
Find the mid point of (2, 3) and (-2,3).
Answer:
(0, 3)
![]()
Question 5.
Find the distance to X – axis from the point (3, – 4).
Answer:
4 units
Question 6.
Find the centroid of the triangle formed by these points (0, 3); (3, 0) and (0, 0).
Answer:
(1, 1)
Question 7.
Where do the points lie on co-ordinate axis ?
(- 4, 0), (2, 0), (6, 0), (- 8, 0)
Answer:
On X-axis.
Question 8.
The graph of y = 5 represents.
Answer:
Parallel to X – axis.
Question 9.
Find sum of the distances from A(3, 4) to X – axis and from B(5, 7) to Y – axis.
Answer:
9 units.
Question 10.
Find the distance from origin to (2,3).
Answer:
\(\sqrt{13}\) units.
Question 11.
Find slope of the line passing through the points (0, sin 60°) and (cos 30°, 0).
Answer:
m = – 1
Question 12.
If the mid point of (x – y, 8) and (2, x + y) is (5, 10), then find (x, y).
Answer:
(10,2)
Question 13.
Where the point (0, 5) lies ?
Answer:
On Y – axis.
Question 14.
Find the area of a triangle whose verti-ces (points) Eire (0, 0), (3, 0) and (0, 4).
Answer:
6 sq. units.
Question 15.
Write the slope of Y – axis.
Answer:
Not defined.
Question 16.
Find the mid point of line segment joined by (4, 5) and (- 6, 3).
Answer:
(-1,4)
![]()
Question 17.
(x, y), (2,0), (3,2) and (1,2) are vertices of a parallelogram, then find (x, y).
Answer:
(0, 0)
Question 18.
Find centroid of a triangle, whose ver-tices are (- a, 0), (0, b) and (a, 0).
Answer:
(0, \(\frac { b }{ 3 }\))
Question 19.
Find the distance between two points A (a cos 0, 0), B (0, a sin 0).
Answer:
a units.
Question 20.
Find the distance between (0, 0), (x1, y1) points.
Answer:
\(\sqrt{\mathrm{x}_{1}^{2}+\mathrm{y}_{1}^{2}}\)
Question 21.
If A(log2 8, log5 25) and B(log10 10, log10 100), then find the mid-point of AB.
Answer:
(2,2)
Question 22.
Find the distance between (0, 7) and (- 7, 0).
Answer:
7\(\sqrt{2}\) units.
Question 23.
Find slope of the line passing through the points (- 1, 1) and (1, 1).
Answer:
0
Question 24.
Find the slope of the line passing through the points (4, 6) and (2, – 5).
Answer:
\(\frac { 11 }{ 2 }\)
Question 25.
In the given figure, find the area of ΔOAB.
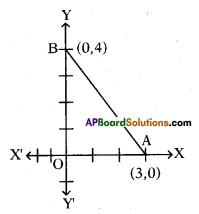
Answer:
6 sq. units.
Question 26.
A line makes 45° with X – axis, then find its slope.
Answer:
m = tan θ = tan 45° = 1
Question 27.
If a line is passing through (2, 3) and (2, – 3), then write the nature of that line.
Answer:
The line is parallel to Y – axis and The slope of the line is not defined.
Question 28.
Find area of the triangle formed by the points A(0, 0), B(1, 0) and C(0, 1).
Answer:
\(\frac { 1 }{ 2 }\) sq. units.
Question 29.
Find the distance from X – axis to (- 4, 3) is units.
Answer:
3 units.
Question 30.
Find the area of the triangle BOA is …………… sq. units.
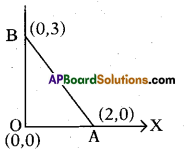
Answer:
3 sq. units.
![]()
Question 31.
Find the slope of the line that passes through the points P (x1, y1) and Q(x2, y2) and making an angle ‘θ’ with X – axis.
Answer:
m = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
Question 32.
The area of given triangle is 60 sq. units, then find x = …………units.
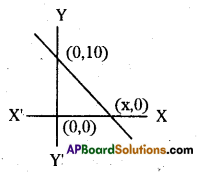
Answer:
12 units.
Question 33.
A line makes 45° with X – axis, then find its slope.
Answer:
1
Question 34.
Find the distance between the points (x1, y1) and (x2, y2) which are on the line parallel to Y – axis.
Answer:
|y – y2| or |y2 – y1 |
Question 35.
If the co-ordinates of the vertices of a rectangle are (0, 0), (4, 0), (4, 3) and (0, 3), then find the length of its di¬agonal.
Answer:
5 units.
Question 36.
Find the distance from Y-axis to (4, 0) is ……………. units.
Answer:
4 units.
Question 37.
Draw the graph represented by y = x.
Question 38.
If origin is the centroid of a triangle, whose vertices are (3, 2), (- 6, y) and (3, – 2), then calculate ‘y’.
Answer:
y = 0
Question 39.
In a coordinate plane, if line segment AB is parallel to X – axis, then write about points A and B.
Answer:
X – coordinates of points A and B are equal.
Question 40.
Find the distance between the points (0, 7) and (- 7, 0).
Answer:
7\(\sqrt{2}\) units.
Question 41.
Find the distance of the point (- 8, 3) from the origin.
Answer:
\(\sqrt{73}\) units
Question 42.
If points (x, 0), (0, y) and (1, 1) are collinear, then find \(\frac{1}{x}+\frac{1}{y}\).
Answer:
1
Question 43.
Write a point on the X – axis is of the form.
Answer:
(x, 0)
Question 44.
Find the points (- 3, 0), (0, 5) and (3, 0) are the vertices of which type of triangle ?
Answer:
Isosceles triangle.
Question 45.
Find the area of the triangle formed by (a, b + c), (b, c + a) and (c, a + b).
Answer:
0
Question 46.
Write a point on the Y – axis is of the form.
Answer:
(0, y)
Question 47.
The point which divides the line segment joining the points (3, 4) and (7, – 6) internally in the ratio 1 : 2 lies in the quadrant.
Answer:
Q4
![]()
Question 48.
Find the distance between the points (- 2, 3) and (2, – 3).
Answer:
\(\sqrt{52}\) units.
Question 49.
AOBC is a rectangle whose three ver-tices are A(4, 0), B(0, 3) and O (0, 0), then find its diagonal ?
Answer:
5 units.
Question 50.
Find the distance of the point (-8, -7) from Y – axis.
Answer:
8 units.
Question 51.
A circle is drawn with origin as centre and passing through (2, 3), then find its radius.
Answer:
\(\sqrt{13}\) units.
Question 52.
Find the perimeter of a triangle whose vertices are A(12, 0), 0(0,.0) and B(0, 5).
Answer:
30 units.
Question 53.
Find the distance of the point (- 4, 3) from X – axis.
Answer:
3 units.
Question 54.
If the distance between the points (4, y) and (1, 0) is 5, then find ‘y’.
Answer:
y = ± 4.
Question 55.
Write the distance of (x, y) from X-axis.
Answer:
y units.
Question 56.
Find the distance of the point (- 9, 40) from the origin.
Answer:
41 units
Question 57.
If (0, 0), (a, 0) and (0, b) are collinear, then write the relation between ‘a’ and b’.
Answer:
ab = 0
Question 58.
Which ratio the centroid divides each median ?
Answer:
2:1
Question 59.
Find the value of ‘p’ if the distance be-tween (2, 3) and (p, 3) is 5. ,
Answer:
p = 7
Question 60.
Find the angle between X – axis and Y – axis.
Answer:
90°
Question 61. Find the distance between the points (a cos θ, 0) and (0, a sin θ).
Answer:
‘a’ units
Question 62.
(- 2, 8) belongs to which quadrant ?
Answer:
Q2
![]()
Question 63.
Find the centroid of the triangle whose vertices are (2, – 3), (4, 6), (- 2, 8).
Answer:
(\(\frac{4}{3}, \frac{11}{3}\))
Question 64.
Guess shape of the closed figure formed by the points (- 2, 0), (2, 0), (2, 2), (0, 4) and (-2,-2).
Answer:
Pentagon
Question 65.
Find the midpoint of the line joining of (2, 3) and (- 2, 3).
Answer:
(0, 0)
Question 66.
If the centroid of the triangle formed with (a, b); (b, c) and (c, a) is O (0, 0), then the value of a3 + b3 + c3.
Answer:
3 abc
Question 67.
If the points (a, 2a), (3a, 3a) and (3,1) are collinear, then find k.
Answer:
k = \(\frac { -1 }{ 3 }\)
Question 68.
Write the coordinates of the midpoint joining P(x1, y1) and Q(x2, y2).
Answer:
\(\left(\frac{\mathrm{x}_{1}+\mathrm{x}_{2}}{2}, \frac{\mathrm{y}_{1}+\mathrm{y}_{2}}{2}\right)\)
Question 69.
Find the slope of line joining of (5, -1), (0, 8).
Answer:
\(-\frac{9}{5}\) =m
Question 70.
If the distance between the points (3, k) and (4, 1) is \(\sqrt{10}\), then find the value of k.
Answer:
4 (or)-2.
Question 71.
If (- 2, – 1), (a, 0), (4, b) and (1,2) are the vertices of a parallelogram, then find a’.
Answer:
a = 1
Question 72.
Write the slope of X – axis.
Answer:
0
Question 73.
P(2, 2), Q(- 4, 4) and R(5, – 8) are the vertices of a ΔPQR, then find length of median from ‘R’.
Answer:
\(\sqrt{157}\) units.
Question 74.
Find the value of ‘k’ if the distance be-tween (2, 8) and (2, k) is 3.
Answer:
k = 5.
Question 75.
Find the distance of a point (α, β) from the origin.
Answer:
\(\sqrt{\alpha^{2}+\beta^{2}}\)
Question 76.
If the points (1, 2), (-1, x) and (2, 3) are collinear, then find the value of x.
Answer:
x = 0.
Question 77.
If (- 2,8) and (6, – 4) are the end points of the diameter of a circle, then find the centre of the circle.
Answer:
(2, 2) = centre.
Question 78.
A(0, -1), B(2, 1) and C(0, 3) are the vertices of AABC, then find median
through ‘B’ has a length . units.
Answer:
2
Question 79.
Two vertices of a triangle are (3, 5) and (- 4, – 5). If the centroid of the triangle is (4, 3), find the third vertex.
Answer:
(13, 9).
Question 80.
If A, B, C are collinear, then find the area of AABC.
Answer:
Δ = 0
![]()
Question 81.
A circle drawn with origin as centre 13
passes through (\(\frac { 13 }{ 2 }\),0). Find the point which doesn’t lie in the interior of the circle.
Answer:
(-6,3)
Question 82.
Find area of triangle formed by (-4, 0), (0, 0) and (0, 5) is ……………… sq. units.
Answer:
10 sq.units.
Question 83.
Find the ratio in which the point (4, 8) divide the line segment joining the points (8, 6) and (0, 10).
Answer:
1:1
Question 84.
Write a formula to the coordinates of the point which divides the line join¬ing (x1, y1) and (x2, y2) in the ratio m: n internally.
Answer:
P = \(\left(\frac{m x_{2}+n x_{1}}{m+n}, \frac{m y_{2}+n y_{1}}{m+n}\right)\)
Question 82.
If A(4, 0), B(8, 0), then find \(\overline{\mathbf{A B}}\).
Answer:
4 units.
Question 83.
Find the slope of the line \(\frac{\mathbf{x}}{\mathbf{a}}+\frac{\mathbf{y}}{\mathbf{b}}\) = 1.
Answer:
m = \(\frac{-\mathrm{b}}{\mathrm{a}}\)
Question 87.
Find .the radius of the circle whose centre is (3, 2) and passes through (- 5, 6) is……………..units.
Answer:
4\(\sqrt{5}\) units.
Question 88.
In Heron’s formula ‘s’ represents.
Answer:
s = \(\frac{a+b+c}{2}\) = Semi perimeter
Question 89.
Slope of the line joining the points (2, 5) and (k, 3) is 2, then find k.
Answer:
k = 1.
Question 90.
If A(4, 5), B(7, 6), then find \(\overline{\mathbf{A B}}\).
Answer:
\(\sqrt{10}=\overline{\mathrm{AB}}\)
Question 91.
Write the distance of (x, y) from Y-axis.
Answer:
‘x’units.
Question 92.
A(2, 0), B(l, 2), C(l, 6), then find ∆ABC.
Answer:
∆ = 0, so the points are collinear.
Question 93.
Find the mid point of the line joining the points (1,1) and (0, 0).
Answer:
( \(\frac{1}{2}, \frac{1}{2}\) )
Question 94.
How much the slope of vertical line ?
Answer:
Not defined.
Question 95.
A(1, – 1), B(0, 6) and C(- 3, 0), then find G (centroid).
Answer:
G = (\(\frac{-2}{3}, \frac{5}{3}\))
Question 96.
A(a, b) and B(- a, – b), then find \(\overline{\mathbf{B A}}\).
Answer:
\(\overline{\mathrm{BA}}=2 \sqrt{\mathrm{a}^{2}+\mathrm{b}^{2}}\)
Question 97.
Find the centroid of the triangle formed with the line x + y = 6 with the coordinate axes.
Answer:
G .= (2, 2)
![]()
Question 98.
Find the area of triangle formed with (- 5,-1), (3,-5) and (5, 2).
Answer:
32 sq. units.
Question 99.
How much the slope of horizontal line?
Answer:
0 = m
Question 100.
Find the angle between the lines x = 2 and y = 3.
Answer:
θ = 90°.
Question 101.
Write the slope of the line y = mx.
Answer:
‘m’
Question 102.
The midpoint of the line joining the points (1, 2) and (1, p) is (1, – 1), then find p.
Answer:
p = – 4.
Question 103.
Name the point of concurrence of me-dians of a triangle is called
Answer:
Centroid
Question 104.
If AC = AB + BC, then the points A, B, C are called points.
Answer:
Collinear
Question 105.
ax + by + c = 0, represents a
Answer:
Straight line
Question 106.
If the points (k, k), (2, 3) and (4, – 1) are collinear, then find k.
Answer:
\(\frac{7}{3}\) = k
Question 107.
Write other name for x-coordinate of a points.
Answer:
Abscissa
Question 108.
Find the slope of the line joining the points A(-1.4, – 3.7) and B(-2.4, 1.3).
Answer:
m = – 5
Question 109.
If a < 0, then (- a, – a) belongs to which quadrant ?
Answer:
Q1
![]()
Question 110.
If θ is the angle made by a line with X – axis, then find slope’m’.
Answer:
m = tan θ
Question 111.
Find the area of square formed with the vertices (0, – 1), (2, 1), (0, 3) and (-2, 1) taken in order as vertices.
Answer:
∆ = 8 sq. units.
Question 112.
Name the person who was introduced coordinate geometry.
Answer:
Rene Descartes
Question 113.
Find the coordinates of centroid of the triangle formed with the vertices (-1,3), (6, -3) and (-3, 6).
Question 114.
In quadrilateral ABCD, AB = BC = CD = AD and \(\overline{\mathbf{A C}} \neq \overline{\mathbf{B D}}\), then it is Answer:……………..type of quadrilateral.
Answer:
Rhombus
Question 115.
Write the slope of the line joining the points (2a, 3b) and (a, – b).
Answer:
m = \(\frac{4 \mathrm{~b}}{\mathrm{a}}\)
Question 116.
Write a formula to distance of (x, y) from origin.
Answer:
\(\sqrt{x^{2}+y^{2}}\)
Question 117.
In rhombus all sides are……………….
Answer:
Equal in length.
Question 118.
If the slope of a line passing through (- 2, 3) and (4, a) is \(\frac { -5 }{ 3 }\), then find Answer:
Answer:
a = – 7.
119.
A(2a, 4a), B(2a, 6a), C(2a+ \(\sqrt{3}\), 5), then write ΔABC is a type of tri¬
angle.
Answer:
Equilateral triangle.
Question 120.
How much each angle in equilateral triangle ?
Answer:
60° = each angle.
Question 121.
In the below figure, G is the centroid then AG : GD = ………………
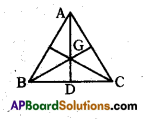
Answer:
2:1
Question 122.
In the below figure AD : GD =
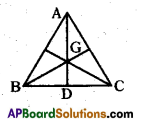
Answer:
3 : 1
Question 123.
Write the midpoint of a line segment divides it in the ratio.
im
Answer:
1 : 1
Question 124.
If the distance between the points (x1, y1) and (x2, y2) is |x1 – x2|, then they are parallel to ……………..
Answer:
x-axis.
Question 125.
Find slope of the line joining the points A(0,0), B(1/2,1/2)
Answer:
1 = m
Question 126.
Write the equation of X – axis.
Answer:
Y = 0
![]()
Question 127.
Write the point of concurrence of alti-tudes of a triangle is called ……………..
Answer:
Orthocentre
Question 128.
P(cos θ, – cos θ), Q (sin θ, sin θ), then find \(\overline{\mathbf{P Q}}\).
Answer:
\(\sqrt{2}\) units.
Question 129.
Diagonals in a parallelogram …………….. to each other.
Answer:
Bisect
Question 130.
Find slope of the line 3x – 2 = 0.
Answer:
Not defined = (\(\frac{0}{3}\))
Question 131.
If A(p, q), B(m, n) and C(p – m, q – n) are collinear, then find pn.
Answer:
qm
Question 132.
Write Y-axis can be represented as.
Answer:
X = 0
Question 133.
Write number of medians of a triangle.
Answer:
3
Question 134.
A(cot θ, 1), B(0, 0), then find \(\overline{\mathbf{B A}}\).
Answer:
cosec θ
Question 135.
If the point (4 – p) lie on X – axis, then find the value of p2 + 2p – 1.
Answer:
– 1
Question 136.
A(t, 2t), B(- 2, 6), C(3, 1) and ΔABC = 5 sq.units, then find ‘t’.
Answer:
t = 2
Question 137.
y-intercept of the line x – 2y + 1 = 0 is …………..
Answer:
b = \(\frac { 1 }{ 2 }\)
Question 138.
In the below figure find ‘x’.
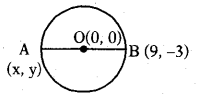
Answer:
-9 = x
Question 139.
In the below figure find ‘y’.
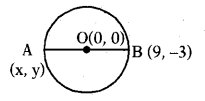
Answer:
3 = y
Question 140.
Where the X and Y axes will inter¬sects ?
Answer:
(0, 0)
Question 141.
If the point (a, 5) lies on Y – axis find the value of ‘a’.
Answer:
a = 0.
Question 142.
Write (3, 0), (8, 0), (1/2, 0) points lie on ………….
Answer:
X – axis.
Question 143.
Nature of the line that does not pass through origin and having a zero slope is
Answer:
Parallel to X – axis.
![]()
Question 144.
Y-intercept of the line y = mx + c is ….
Answer:
‘c’
Question 145.
In ΔABC, all the side are different, then it is called type of triangle.
Answer:
Scalene
Question 146.
A = (\(\frac{1}{2}, \frac{3}{2}\)) , B = (\(\frac{3}{2}, \frac{-1}{2}\)) then find \(\overline{\mathbf{B A}}\)
Answer:
\(\sqrt{5}\)
Question 147.
Find the area of below parallelogram, if ΔABC = 5 sq. units.
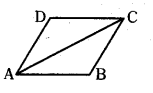
Answer:
10 sq. units
Question 148.
Find x-intercept of the line x – y +1 =0.
Answer:
– 1
Question 149.
In ΔPQR, PQ = QR, then it is called ……………… triangle.
Answer:
Isosceles
Question 150.
If (1, x) is at \(\sqrt{10}\) units from origin, then find the value of ‘x’.
Answer:
x = ± 3
Question 151.
A(1, – 1), B(2 1/2, 0), C(4, 1), then find area of ΔABC.
Answer:
Δ = 0.
Question 152.
Name the line joining the mid point of one side of a triangle from opposite vertex is called …………….
Answer:
Median
Question 153.
Find angle made by the line y = x with the positive direction of X – axis.
Answer:
45°.
Choose the correct answer satistying the following statements.
Question 154.
Statement (A): The point (0, 4) lies on Y – axis.
Statement (B) : The X co-ordinate of the point on Y – axis zero.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)
Question 155.
Statement (A): The value of y is 6, for which the distance between the points P(2, – 3) and Q(10, y) is 10.
Statement (B): Distance between two given points A(x1, y1) and B(x2, y2) is given by
AB = \(\sqrt{\left(x_{2}+x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(iii)
Question 156.
Statement (A) : The point (- 1, 6) di¬vides the line segment joining the points (- 3, 10) and (6, – 8) in the ratio 2 : 7 internally.
Statement (B): Three points A, B and C are collinear if area of AABC = 0.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)
Question 157.
Statement (A) : Centroid of a triangle formed by the points (a, b), (b, c) and (c, a) is at origin, then a + b + c = 0.
Statement (B) : Centroid of a AABC with vertices A(x1, y1), B(x2, y2) and C(x3, y3) is given by
\(\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right)\)
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)
![]()
Question 158.
Statement (A): The area of the triangle with vertices (- 5,-1), (3, – 5), (5, 2) is 32 square units.
Statement (B): The point (x, y) divides the line segment joining the points A(xj, y2) and B(x2, y2) in the ratio k : 1 externally, then
\(x=\frac{k x_{2}+x_{1}}{k+1}, y=\frac{k y_{2}+y_{1}}{k+1}\)
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(ii)
Question 159.
Statement (A): The ratio in which the segment joining the points (-3, 10) and (6, – 8) is divided by (- 1, 6) is 2 : 7.
Statement (B) : If A(x1, y1), B(x2, y2) are two points. Then the point C(x, y) such that C divides AB internally in the ratio k : 1 is given by
x = \(\frac{\mathrm{kx}_{2}+\mathrm{x}_{1}}{\mathrm{k}+1}, \mathrm{y}=\frac{\mathrm{ky}_{2}+\mathrm{y}_{1}}{\mathrm{k}+1}\)
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)
Question 160.
Statement (A) : If three vertices of a parallelogram taken in order are (- 1, – 6), (2, – 5) and (7, 2), then its fourth vertex is (4, 1).
Statement (B) : Diagonals of a paral-lelogram bisect each other.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)
Question 161.
Statement (A) : The points (k -I- 1, 1), (2k + 1, 3) and (2k + 2, 2k) are col- linear, then k = 4.
Statement (B) : Three points A(x1, y1), B(x2, y2) and C(x3, y3) are collinear if and only if
x1(y2 – y3) + x2(y3-y1) + x3(y1-y2) = 0
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(iii)
Question 162.
Statement (A) : Let the vertices of a ΔABC are A(- 5, – 2), B(7, 6) and C(5, – 4), then coordinate of circum- centre is (1, 2).
Statement (B) : In a right angle tri¬angle, mid-point of hypotenuse is the circumcentre of the triangle.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)
Question 163.
Statement (A): If A(2a, 4a) and B(2a, 6a) are two vertices of a equilat¬eral triangle ABC, then the vertex C is given by (2a + a\(\sqrt{3}\) , 5a).
Statement (B): In equilaterahtriangle all the coordinates of three vertices can be rational.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(ii)
Question 164.
Statement (A) : The equation of the straight line which passes through the point (2,-3) and the point of the inter-section of the lines x + y + 4 = 0 and 3x – y – 8 = 0 is 2x – y – 7 = 0.
Statement (B) : Product of slopes of two perpendicular straight lines is – 1.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)
Read Che below passages and answer to the following questions.
Let there be two points (4, 1) and (5,-2) in a two dimensional coordi¬nate system. A line which passes through the above give points and intersects the coordinate axes forms a triangle.
Question 165.
Write the equation of the line passing through the above given points.
Answer:
3x + y – 13 = 0.
Question 166.
Find the point of intersection of the above line with both the coordinate axes.
Answer:
(\(\frac { 13 }{ 3 }\),0) and (0, 13).
Question 167.
Find the area of the triangle so formed.
Answer:
\(\frac { 169 }{ 6 }\) sq. units.
In the diagram on a Lunar eclipse, if the position of Sun, Earth and Moon are shown by (- 4, 6) (k, – 2) and (5, – 6) respectively.
Question 168.
In Lunar eclipse what is the positions of Sun, Earth and Moon ?
Answer:
All are in same line, i.e., collinear.
Question 169.
To solve the above problem which mathematical concept is used ?
Answer:
Co-ordinate Geometry.
![]()
Question 170.
Which formula is used to find the value of k ?
Δ = \(\frac { 1 }{ 2 }\) |x1(y2 – y3) + x2(y3-y1) + x3(y1 – y2) | = 0
Manowbhiram calculated the dis¬tance between T(5, 2) and R(-4, -1) to the nearest length is 9.5 units.
Question 171.
Do you agree with Manowbhiram ?
Answer:
Yes, I agree with him.
Question 172.
Which mathematical concept is used to you support Manowbhiram ?
Answer:
Co-ordinate Geometry (or) (Distance formula).
Question 173.
Column – II gives distance between pair of points given in column -I, match them correctly.

Answer:
A – (iv), B – (i)
Question 174.
Column – II gives distance between pair of points given in column -I, match them correctly.

Answer:
A – (ii), B – (iii)
Question 175.
Column – II gives the coordinates of the point ’p’ that divides the line segment join¬ing the points given in column -I, match them correctly.

Answer:
A – (iv), B – (ii)
Question 176.
Column – II gives the coordinates of the point ‘p’ that divides the line segment join¬ing the points given in column -I, match them correctly.

Answer:
A – (iii), B – (i).
Question 177.
Column – II gives the area of triangles whose vertices are given in column -1, match them correctly.

Answer:
A – (iv), B – (iii).
Question 178.
Column – II gives the area of triangles whose vertices are given in column -1, match them correctly.

Answer:
A – (ii), B – (i).
Question 179.

Answer:
A – (iv), B – (iii).
Question 180.

Answer:
A – (iii), B – (i).
![]()
Question 181.
Name the quadrilateral, which satis¬fies both the conditions given below.
Statement (A) : Diagonals are equal
Statement (B) : All sides are equal
a) Rhombus
b) Parallelogram
c) Rectangle
d) Square
Answer:
(d)
Question 182.
Find the area of the shaded triangle, in the figure given below.
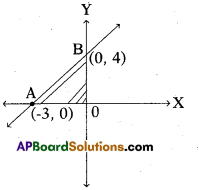
Answer:
6 sq. units
Question 183.
What is the slope of the line joining the points (2, 0) and (- 2, 0).
Solution:
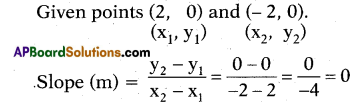
Question 184.
Name the point which is the point of intersection of medians of a triangle.
Answer:
Centroid of a triangle.