Practice the AP 10th Class Maths Bits with Answers Chapter 5 Quadratic Equations on a regular basis so that you can attempt exams with utmost confidence.
AP State Syllabus 10th Class Maths Bits 5th Lesson Quadratic Equations with Answers
Question 1.
If x2 – px + q = 0(p,q∈R and p ≠ 0, q ≠ 0) has distinct real roots, then write
the condition.
Answer: p2 > 4q.
Question 2.
If one root of 2x2 + kx – 6 is 2., then find k.
Answer:
k = – 1
Explanation:
2(2)2 + k(2) – 6 = 0
⇒ 8 + 2k – 6 = O
⇒ 2k + 2 = 0 ⇒ k = -1
Question 3.
If the equation x2 + 5x + k = 0 has real and distinct roots, then find the value of ‘k’.
Answer:
k > 6.25
Explanation:
Real and distinct roots so,
b2 – 4ac > 0
⇒ 25 – 4 . 1. k > 0
⇒ 25 > 4k = k > \(\frac{25}{4}\) > 6.25
![]()
Question 4.
Frame a quadratic equation, whose roots are 2 + \(\sqrt{3}\) and 2 – \(\sqrt{3}\) ?
Answer:
x2 – 4x + 1 = 0
Explanation:
x2 – (2 + \(\sqrt{3}\) +2 – \(\sqrt{3}\))x + (2 + \(\sqrt{3}\)) (2 – \(\sqrt{3}\))
⇒ x2 – 4x + 1 = 0
Question 5.
In a quadratic equation ax2 + bx + c = 0, if b2 – 4ac > 0, then write the nature of the roots.
Answer:
Roots are real and distinct.
Question 6.
Create the quadratic equation, whose zeroes are \(\sqrt{2}\) and – \(\sqrt{2}\) ?
Answer:
x2 – 2 = 0.
Explanation:
\(x^{2}-(\sqrt{2}-\sqrt{2}) x+(\sqrt{2})(-\sqrt{2})=0\)
⇒ x2 – 2 = 0
Question 7.
For which positive value of x the qua-dratic equation 4x\(\sqrt{3}\) -9 = 0 satisfies ?
Answer:
\(\frac{3}{2}\)
Question 8.
If the roots of x2 + 6x + 5 = 0 are a and P, then find the value of sum of the roots.
Answer:
-6
Explanation:
α + β = \(\frac{-b}{a}\) = — 6
Question 9.
Write the discriminant of 6x2 – 5x + 1 = 0.
Answer:
D = 1
Explanation:
D = b2 – 4ac = 25 – 4 . 6 . 1
⇒ 25 – 24 = 1 > 0 D = 1
Question 10.
Write the quadratic polynomial having \(\frac { 1 }{ 3 }\) and \(\frac { 1 }{ 2 }\) as its zeroes.
Answer:
x2 – \(\frac{5 x-1}{6}\) = 0 ⇒ 6x2 – 5x + 1 = 0
Explanation:
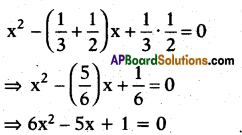
Question 11.
If a number is 132 smaller than its square, then find the number.
Answer:
12
Explanation:
x + 132 = x2
⇒ x2 – x – 132 = 0
By solve the equation, ∴ x = 12
Question 12.
Write the general form of a quadratic equation in variable ‘x’.
Answer:
ax2 + bx + c = 0 (a ≠ 0).
Question 13.
Make the quadratic polynomial, whose zeroes are 2 and 3.
Answer:
x2 – 5x + 6.
Question 14.
If α, β are the roots of x2 – 10x + 9 = 0, thep find the value of | α – β |.
Answer:
8
Explanation:
x2 – 9x – x + 9 = 0
⇒ x(x – 9) – 1 (x – 9) = 0
⇒ (x-9)(x- 1) = 0
x = 9 and 1, |α – β| = |9- 1| = 8
Question 15.
Write the discriminant of adjacent dia-gram indicates.
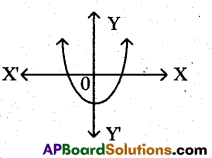
Answer:
b2 – 4ac > 0.
Question 16.
If the roots of a quadratic equation px2 + qx + r = 0 are imaginary, then write the condition of discriminant.
Answer:
q2 < 4pr (or) q2 – 4pr < 0.
![]()
Question 17.
Two angles are complementary. If the large angle is twice the measure of a smaller angle, then find the value of smaller angle.
Answer:
30°
Explanation:
x + y = 90°
⇒ x + 2x = 90°
⇒ 3x = 90° ⇒ x = 30°
Question 18.
Observe the following graphs.
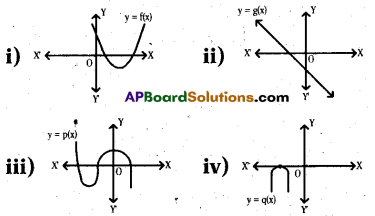
Which as them are the graphs of qua-dratic polynomials ?
Answer:
(i) and (iv).
Question 19.
Write the possible number of roots to a quadratic equation.
Answer:
At a maximum of 2.
Question 20.
If 1 is a common root of ax2 + ax + 2 = 0 and x2 + x + 6 = 0, then find a-b.
Answer:
2
Question 21.
Find the product of roots of quadratic equation ax2 + bx + c = 0.
Answer:
\(\frac{\text { c }}{\text { a }}\)
Question 22.
Write the number of diagonals in a polygon, having ‘n’ sides.
Answer:
\(\frac{n(n-3)}{2}\)
Question 23.
Find the discriminant of quadratic equation 2x2 + x – 4 = 0.
Answer:
33
Question 24.
A quadratic equation ax2 + bx + c = 0 has two distinct real roots, then write the condition.
Answer:
b2 – 4ac >0.
Question 25.
Draw the shape of quadratic equation which having distinct roots ?
Answer:
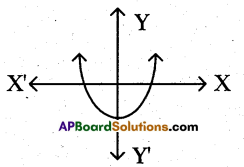
Question 26.
The sum of a number and its reciprocal is \(\frac { 5 }{ 2 }\) then find the number.
Answer:
2 or \(\frac { 1 }{ 2 }\)
Explanation:
x + \(\frac{1}{x}=\frac{5}{2}\)
⇒ \(\frac{x^{2}+1}{x}=\frac{5}{2}\)
⇒ 2x2 + 2 = 5x
⇒ 2x2 – 5x + 2 = 0
⇒ 2x2 – 4x r x + 2 = 0
⇒ 2x(x – 2) – 1 (x – 2) – 0 ⇒ (x – 2) (2x – 1) = 0 1
∴ x = 2 or 1/2.
![]()
Question 27.
Find the roots of the equation 4x2 – 4\(\sqrt{3}\) x + 3 = 0.
Answer:
\(-\frac{\sqrt{3}}{2}\)
Question 28.
Find the positive root of \(\sqrt{3 x^{2}+6}=9\)
Answer:
5
Explanation:
3x2 + 6 = 81
⇒ 3x2 = 81 – 6 = 75
⇒ x2 = \(\) = 25 ⇒ x = 5
Question 29.
Find the roots of the quadratic equation (7x – 1) (2x + 3) = 0.
Answer:
\(\frac{1}{7}, \frac{-3}{2}\)
Question 30.
If the sum of the squares of two con-secutive odd numbers is 74, then find the smaller number.
Answer:
5 (or)-7
Explanation:
(2x + 1)2 + (2x + 3)2 – 74
⇒ 4x2 + 4x + 1 + 4x2 + 12x + 9 — 74′
⇒ 8x2 + 16x + 10 = 74
⇒ 8x2 + 16x – 64 = 0
⇒ 8(x2 + 2x – 8) = 0
⇒ x2 + 4x – 2x – 8 = 0
⇒ x(x + 4) – 2 (x + 4) = 0
⇒ x = – 4, 2
∴ x = – 4, then smaller number
= 2 . (-4) + 1 = -8 + 1 = -7
∴ x = 2, then smaller number
= 2 . (2) + 1 = 4 + 1 = 5
Question 31.
Write the standard form of a cubic polynomial.
Answer:
ax3 + bx2 + cx + d = 0; (a ≠ 0).
Question 32.
Write the discriminant of 5x2– 3x – 2 = 0.
Answer:
49
Question 33.
Create the quadratic equation whose roots are – 2 and – 3.
Answer:
x2 + 5x + 6 = 0
Question 34.
Find the roots of the quadratic equation \(\frac{x^{2}-8}{x^{2}+20}=\frac{1}{2}\)
Answer:
±6
Explanation:
2x2 – 16 = x2 + 20
⇒ x2 – 36 ⇒ x = ±6.
Question 35.
Find the roots of the equation 3x2 – 2\(\sqrt{6}\) x + 2 = 0.
Answer:
\(\sqrt{\frac{2}{3}}, \sqrt{\frac{2}{3}}\)
Question 36.
Find the roots of the quadratic equa- tion \(\left(x-\frac{1}{3}\right)^{2}\) = 9.
Answer:
\(\frac { 10 }{ 3 }\) (or) \(\frac { -8 }{ 3 }\).
Explanation:
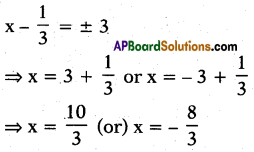
Question 37.
On solving x2 + 5 = – 6x, find the value of ‘x’
Answer:
– 1 or – 5.
Question 38.
Simplified form of \(\frac{\mathbf{x}}{\mathbf{x}-\mathbf{y}}-\frac{\mathbf{y}}{\mathbf{x}+\mathbf{y}}\)
Answer:
\(\frac{x^{2}+y^{2}}{x^{2}-y^{2}}\)
Question 39.
Find the sum of roots of bx2 + ax + c = 0.
Answer:
\(\frac{-a}{b}\)
![]()
Question 40.
Find the roots of 2x2 – x + \(\frac { 1 }{ 8 }\) = 0.
Answer:
\(\frac{1}{4}, \frac{1}{4}\)
Question 41.
If x + \(\frac{1}{x}\) = 2, then find \(x^{2}+\frac{1}{x^{2}}\).
Answer:
2
Explanation:
x + \(\frac { 1 }{ x }\) = 2
⇒ \(x^{2}+\frac{1}{x^{2}}\) + 2 = 4 ⇒ x2 + \(x^{2}+\frac{1}{x^{2}}\) = 2
Question 42.
If 3y2 — 192, then find ‘y’.
Answer:
y = ± 8
Question 43.
How many diagonals has a pentagon?
Answer:
’9′
Question 44.
If α and β are the roots of the quadratic equation x2 – 3x + 1 = 0, then find \(\left(\frac{1}{\alpha^{2}}+\frac{1}{\beta^{2}}\right)\)
Answer:
7
Question 45.
If \(\mathbf{a}^{\mathbf{x}^{2}-4 \mathbf{x}+3}\) = 1, then find x (a # 0).
Answer:
1 or 3.
Question 46.
Find discriminant of the quadratic equation x + \(\frac { 1 }{ x }\) = 3.
Answer:
5
Question 47.
Create the quadratic equation with 2 < x < 3.
Answer:
x2 – 5x + 6 < 0.
Explanation:
x2 – (2 + 3)x + 2 . 3 < 0
⇒ x2 – 5x + 6 < 0
Question 48.
p(x) = x2 + 2x + 1, then find p(x2).
Answer:
x4 + 2x2 + 1
Question 49.
x2 – 7x – 60 = 0, then find ‘x’.
Answer:
12 and -5.
Question 50.
\(\frac{1}{a+3}+\frac{1}{a-3}+\frac{6}{9-a^{2}}\) is equal to ?
Answer:
\(\frac{2}{a+3}\)
Question 51.
Find the roots of \(\sqrt{2} x^{2}+7 x+5 \sqrt{2}\) = 0.
Answer:
\(\frac{-5}{\sqrt{2}} \text { or }-\sqrt{2}\)
Question 52.
Find the roots of a quadratic equation \((\sqrt{2} x+3)(5 x-\sqrt{3})=0\)
Answer:
\(\frac{-3}{\sqrt{2}}, \frac{\sqrt{3}}{5}\)
Question 53.
4x2 + ky – 2 = 0 has no real roots, then find ‘k’.
Answer:
k < – \(\sqrt{32}\)
![]()
Question 54.
The sum of a number and its reciprocal is \(\frac { 50 }{ 7 }\), then find the number.
Answer:
7 (or) \(\frac { 1 }{ 7 }\)
Explanation:
x + \(\frac{1}{x}=\frac{50}{7}\)
⇒ \(\frac{x^{2}+1}{x}=\frac{50}{7}\)
⇒ 7x2 + 7 — 50x
⇒ 7x2 – 50x + 7 — 0
⇒ 7x2 – 49x – x + 7 = 0
⇒ 7x (x – 7) – 1 (x – 7) – 0
⇒ (x – 7) (7x – 1) – 0
=+ x = 7 (or) 1/7
Question 55.
Find the roots of the quadratic equation \(\frac{9}{x^{2}-27}=\frac{25}{x^{2}-11}\)
Answer:
±6;
Question 56.
Write the nature of the roots of a qua-dratic equation 4x2 – 12x + 9 = 0.
Answer:
Real and equal.
Question 57.
3x2 + (- k)x + 8 = 0 has no real roots, then find k’.
Answer:
k < 4\(\sqrt{6}\)
Explanation:
No real roots. So D < 0,
(-k)2 – 4 . 3 . 8 < 0
⇒ k2 – 96 < 0
⇒ k2 < 96
⇒ k < \(\sqrt{96}\)
⇒ k < \(4 \sqrt{6}\)
Question 58.
Find the discriminant of 3x2 – 2x = \(\frac{-1}{3}\).
Answer:
D = 0
Question 59.
Find the product of the roots of 1 =x2.
Answer:
-1
Question 60.
x(x + 4) = 12, then find ‘x’.
Answer:
– 6 or 2.
Question 61.
Form a quadratic equation from, x3 – 4x2 – x + 1 = (x – 2)3.
Answer:
2x2 – 13x + 9 = 0.
Explanation:
x3 – 4x2 – x + 1 = x3 – 3 . x2 . 2 + 3 . x . 22 – 23
⇒ x3 – 4x2 – x + 1 = x3 – 6x2 + 12x – 8
⇒ x3 – 4x2 – x + 1 = x3 + 6x2 – 12x + 8 = 0
⇒ 2x2 – 13x + 9 = 0
Question 62.
Find the product of the roots of x2 + 7x = 0.
Answer:
0
Question 63.
\(\frac{2 a^{2}+a-1}{a+1}+\frac{3 a^{2}+5 a+2}{3 a+2}+\frac{4-a^{2}}{a+2}\) is equal to ?
Answer:
2 (a +1)
Question 64.
1 and \(\frac { 3 }{ 2 }\) are the roots of which qua-dratic equation ?
Answer:
2x2 – 5x + 3 = 0.
Question 65.
If b2 < 4ac, then draw the shape of graph.
Answer:
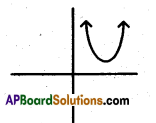
Question 66.
\(\sqrt{\mathbf{k}+\mathbf{1}}\) = 3, then find ‘k’.
Answer:
k = 8
Question 67.
\(\sqrt{x}=\sqrt{2 x-1}\), then find ‘x’.
Answer:
x = 1
![]()
Question 68.
If \(\frac{1}{x-2}+\frac{2}{x-1}=\frac{6}{x}\) then find ‘x’
Answer:
3 or \(\frac { 4 }{ 3 }\)
Question 69.
Find the coefficient of ‘x’ in a pine qua-dratic equation.
Answer:
0
Question 70.
Write number of distinct line segments that can be formed out of n – points.
Answer:
\(\frac{n(n-1)}{2}\)
Question 71.
The product of two consecutive positive integers is 306, then find the largest number.
Answer:
18
Explanation:
x(x + 1) = 306 ⇒ x2 + x – 306 = 0
by solving thik Q.E., x = 17
∴ Largest number = x + 1
= 17 + 1 = 18.
Question 72.
Write the nature of roots of 3x2 + 13x – 2 = 0.
Answer:
Real and unequal.
Question 73.
If α and β are the roots of x2 – 2x + 3 = 0, then find α2 + β2
Answer:
α2 + β2 = – 2.
Question 74.
If (2x – 1) (2x + 3) = 0, then find ‘x’.
Answer:
\(\frac { 1 }{ 2 }\) or \(\frac { -3 }{ 2 }\)
Question 75.
Write the quadratic equation whose one root is 2 – \(\sqrt{3}\) .
Answer:
x2 – 4x + 1 = 0
Question 76.
If b2 – 4ac > 0, then write nature of the roots of the quadratic equation.
Answer:
Real and distinct.
Question 77.
Find product of the roots of ax2 + bx + c = 0. c
Answer:
c/a
Question 78.
Write the nature of the roots of a qua-dratic equation 4x2 + 5x + 1 = 0.
Answer:
Real and distinct.
Question 79.
Write the quadratic equation whose roots are – 1,6.
Answer:
x2 – 5x – 6 = 0.
Question 80.
Create the quadratic equation whose roots are – 3 and – 4.
Answer:
x2 + 7x 4- 12 = 0.
Question 81.
Find the roots of the quadratic equation (3x + 4)2 – 49 = 0.
Answer:
1, \(\frac{-11}{3}\)
Question 82.
If x2 – 2x + 1 = 0, then find x + \(\frac{1}{x}\).
Answer:
2
Question 83.
Write nature of the roots of 5x2 – x + 1 = 0.
Answer:
Imaginary roots.
![]()
Question 84.
Write the nature of the roots of qua-dratic equation 3x2 + x + 8 = 0.
Answer:
Imaginary roots.
Question 85.
Find product of the roots of the qua-dratic equation 3x2 – 6x + 11 = 0.
Answer:
\(\frac{11}{3}\)
Question 86.
Form a quadratic equation whose roots are k and 1/k.
Answer:
x2 – (\(\mathrm{k}+\frac{1}{\mathrm{k}}\))x + 1 = 0
Question 87.
If k2 – 8kx + 16 = 0 has equal roots, then find the value of ‘k’.
Answer:
k = ± 1.
Explanation:
(-8k)2 – 4(1) (16) = 0
⇒ 64k2 = 64 ⇒ k2 = 1 ⇒ k = ±1
Question 88.
If the roots of a quadratic equation ax2 + bx + c = 0 are real and equal, then find ‘b2‘.
Answer:
4ac
Question 89.
3(x – 4)2 – 5(x – 4) = 12, then find ‘x’.
Answer:
7 (or) 8/3.
Explanation:
3(x – 4)2 – 5 (x – 4) = 12
3[x2 + 16 – 8x] – 5x + 20 — 12
3x2 + 48 – 24x – 5x + 20 – 12 — 0
⇒ 3x2 – 29x + 56 = 0
⇒ 3x2 – 21x – 8x + 56 — 0
⇒ 3x (x – 7) – 8 (x – 7) = 0
⇒ (x – 7) (3x – 8) = 0
⇒ x = 7 (or) x = \(\frac { 8 }{ 3 }\)
Question 90.
If a and pare the roots of x2 + x + 1 = 0, then find α2 + β2.
Answer:
α2 + β2 = – 1.
Question 91.
\(\frac{1-\frac{1}{1+x}}{\frac{1}{1+x}}\) is equal to ?
Answer:
x
Question 92.
Find sum of the roots of a pure quadratic equation.
Answer:
0
Question 93.
\(\frac{\mathbf{x}}{\mathbf{a}-\mathbf{b}}=\frac{\mathbf{a}}{\mathbf{x}-\mathbf{b}}\) , then find ‘x’.
Answer:
b – a (or) – a
Question 94.
\(\frac{1}{x+4}-\frac{1}{x-7}=\frac{11}{30}\) x ≠ -4 x or 7 find x’.
Answer:
2 or 1
Question 95.
(1 – 5x) (9x +1) is equal to ?
Answer:
1 + 4x – 5x2.
Question 96.
From the figure, find ’x’.
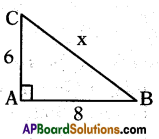
Answer:
± 10
Explanation:
By Pythagoras theorem,
x2 = 62 + 82 = 64 + 36 = 100
x = \(\sqrt{100}\) = ± 10
![]()
Question 97.
Find the sum of the roots of the equation 3x2 – 7x + 11 = 0.
Answer:
7/3
Question 98.
Find the roots of the quadratic equation \((\sqrt{5} x-3)(\sqrt{5} x-3)\) – 0.
Answer:
\(\frac{3}{\sqrt{5}}, \frac{3}{\sqrt{5}}\)
Question 99.
Write the nature of the roots of the quadratic equation \(\sqrt{3} x^{2}-2 x-\sqrt{3}\).
Answer:
Real and distinct.
Question 100.
If 5x2 – kx + 11 = 0 has root x = 3, then find ’k’.
Answer:
k = \(\frac{56}{3}\)
Explanation:
5(3)2 – k(3) + 11 = 0
⇒ 45 + 11 – 3k = 0
⇒ 56 – 3k = 0
⇒ 3k = 56 ⇒ k = \(\frac { 56 }{ 3 }\)
Question 101.
Find the value of ‘p’ for which 4x2 – 2px + 7 = 0 has a real roots.
Answer:
p > 2\(\sqrt{7}\)
Question 102.
If one root of a quadratic equation is 7 – 7\(\sqrt{3}\) , then find the quadratic equation.
Answer:
x2 – 14x + 46 = 0.
![]()
Question 103.
If b2 – 4ac = 0, then write nature of the roots of the quadratic equation.
Answer:
Real and equal.
Question 104.
Find sum of the roots of ax2 + bx + c = 0.
Answer:
\(-\frac{b}{a}\)
Question 105.
If the equation x2 – kx + 1 = 0 has equal roots, then find the value of ‘k’.
Answer:
k = ± 2
Explanation:
b2 – 4ac = (- k)2 – 4 . 1 . 1 = 0
⇒ k2 – 4 = 0
⇒ k2 = 4 ⇒ k = \(\sqrt{4}\) = ± 2.
Question 106.
Find (he product of the roots of the qua-dratic equation \(\sqrt{2} \mathrm{x}^{2}-3 \mathrm{x}+5 \sqrt{2}\) = 0.
Answer:
5
Question 107.
Write the nature of roots of 3x2 + 6x – 2 = 0.
Answer:
Real and distinct.
Question 108.
If the sum of the roots of the quadratic equation 3x2 + (2k + 1)x – (k + 5) = 0 is equal to the product of the roots, then find the value of k.
Answer:
4
Explanation:
Sum of the roots = product of the roots
⇒ \(\frac{-(2 k+1)}{3}=\frac{-(k+5)}{3}\)
⇒ – 2k- 1 = -k – 5 ⇒ k = 4
![]()
Question 109.
Find the product of zeroes in the above equation.
Answer:
\(\frac{-11}{5}\)
Question 110.
Find the degree of any quadratic equation.
Answer:
2
Question 111.
In the quadratic equation
x2 + x – 2 = 0, find the value of a + b + c.
Answer:
a + b + c = 0.
Question 112.
Find the value of \(\left(x+\frac{1}{x}\right)^{2}-\left(y+\frac{1}{y}\right)^{2}-\left(x y-\frac{1}{x y}\right) \cdot\left(\frac{x}{y}-\frac{y}{x}\right)\)
Answer:
0
Question 113.
Form a quadratic equation from x(2x + 3) = x2 + 1.
Answer:
x2 + 3x – 1 = 0.
Explanation:
2x2 + 3x = x2 + 1
⇒ x2 + 3x – 1 = 0
Question 114.
(x – α) (x – β) = 0, then find the product.
Answer:
x2 – (α + β)x + αβ = 0.
Question 115.
If α and β are die roots of x2 – 5x + 6 = 0, then find the value of α – β.
Answer:
± 1.
Question 116.
For what values of m’ are the roots of the equation mx2 + (m + 3)x + 4 = 0 are equal ?
Answer:
9 or 1.
Explanation:
(m + 3)2 – 4 . m . 4 = 0
⇒ (m + 3)2 – 16m = 0
⇒ m2 + 9 + 6m- 16m = 0
⇒ m2 – 10m + 9 = 0
⇒ m2 – 9m – m + 9 = 0
⇒ m(m – 9) – 1 (m – 9) = 0
∴ m = 9 or 1
Question 117.
Find the roots of 2x2 + x – 4 = 0.
Answer:
x = \(\frac{-1 \pm \sqrt{33}}{4}\)
Question 118.
If kx (x – 2) + 6 = 0 has equal roots, then find k’.
Answer:
k = 6.
Explanation:
kx2 – 2kx + 6 = 0
⇒ (2k)2 – 4 . k . 6 = 0
⇒ 4k2 – 24k = 0
⇒ 4k (k – 6) = 0 ⇒ k = 6
Question 119.
If ‘2’ is a root of x2 + 5x + r = 0, then find ‘r’.
Answer:
r = -14
Question 120.
(α + β)2 – 2αβ is sequal to ……………
Answer:
α2 + β2
Question 121.
Find the value of \(\sqrt{\mathbf{a}+\sqrt{\mathbf{a}+\sqrt{\mathbf{a + \ldots \ldots \infty}}}}\)
Answer:
\(\frac{1+\sqrt{1+4 a}}{2}\)
Question 122.
If the sum of the roots of kx2 – 3x + 1 = 0 is \(\frac{-4}{3}\) then find ‘k’.
Answer:
\(\frac{-9}{4}\)
Explanation:
\(\frac{3}{\mathrm{k}}=\frac{-4}{3} \Rightarrow \frac{3 \times 3}{-4}=\mathrm{k} \Rightarrow \mathrm{k}=\frac{-9}{4}\)
Question 123.
\(\frac{n(n+1)}{2}\) = 55, then find ‘n’
Answer:
10
Explanation:
⇒ n2 + n = 110 = 0
⇒ n2 + n – 110 = 0
⇒ n = 10
![]()
Question 124.
If ‘α’ is β root of ax2 + bx + c = 0, then find aα2 + bα + c.
Answer:
0
Question 125.
If α and β are the roots of the quadratic equation 2x2 + 3x – 7 = 0, then find \(\frac{\alpha^{2}+\beta^{2}}{\alpha \beta}\)
Answer:
\(\frac{-37}{14}\)
Question 126.
Find the sum of the roots of -7x + 3x2 – 1 = 0.
Answer:
\(\frac{7}{3}\)
Question 127.
Find the roots of a quadratic equation \(\frac{\mathbf{x}}{\mathbf{p}}=\frac{\mathbf{p}}{\mathbf{x}}\)
Answer:
x = p
Explanation:
x2 = p2 ⇒ x = p
Question 128.
If (x – 3) (x + 3) = 16, then find the value of ‘x’.
Answer:
± 5.
Question 129.
Write the roots of a quadratic equation ax2 + bx + c = 0.
Answer:
x = \(\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
Question 130.
Find the sum of the roots of the quadratic equation 5x2 + 4\(\sqrt{3}\)x – 11 = 0.
Answer:
\(\frac{-4 \sqrt{3}}{5}\)
Question 131.
If one root of x2 – (p – 1)x + 10 = 0 is 5, then find ‘p’.
Answer:
7
Explanation:
52 – (p – 1) 5 + 10 = 0
⇒ 25 + 10 – 5p + 5 = 0
⇒ 35 = 5p ⇒ p = 7
Question 132.
If one root of x2 – x + k = 0 is square of other, then find ‘k’.
Answer:
k = cube of one root
Explanation:
α = x, β = x2
Product of roots = αβ = \(\frac{\mathrm{c}}{\mathrm{a}}\)
⇒ x.x2 = k ⇒ k = x3
k is cube of the first root.
Question 133.
If α, β are the roots of x2 – px + q = 0, then find α3 + β3.
Answer:
p3 – 3pq
Question 134.
x2 + (x + 2)2 = 290, then find ‘x’.,
Answer:
11 or – 13
Question 135.
Find the value of \(\sqrt{\mathbf{a} \sqrt{\mathbf{a} \sqrt{\mathbf{a}} \ldots \ldots \infty}}\)
Answer:
a
Question 136.
If \(\frac{-7}{3}\) is a root of 6x2 – 13x – 63 = 0, then find other root.
Answer:
\(\frac{9}{2}\)
Question 137.
If b22 – 4ac < 0, then write nature of the roots of the quadratic equation.
Answer:
Imaginary roots.
Choose the correct answer satistying the following statements.
Question 138.
Statement (A) : The equation x2 + 3x + 1 = (x – 2)2 is a quadratic equation.
Statement (B) : Any equation of the form ax2 + bx + c = 0 where a ± 0, is called a quadratic equation.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(iii)
Explanation:
We have, x2 + 3x + 1 = (x – 2)2
⇒ x2 + 3x + 1 = x2 – 4x + 4
⇒ 7x – 3 = 0, it is not of the form ax2 + bx + c = 0
So, A is incorrect but B is correct.
Hence (iii) is the correct option.
![]()
Question 139.
Statement (A) : The roots of the qua-dratic equation x2 + 2x + 2 = 0 are imaginary.
Statement (B) : If discriminant D = b2 – 4ac < 0, then the roots of quadratic equation ax2 + bx + c = 0 are imaginary.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)
Explanation:
x2 + 2x + 2 = 0
∴ Discriminant, D = b2 – 4ac
= (2)2 – 4 x 1 x 2
= 4 – 8 = -4 < 0
∴ Roots are imaginary.
So, both A and B are correct and B explains Answer: Hence, (i) is the correct option.
Question 140.
Statement (A) : The value of k = 2, if one root of the quadratic equation
6x2 – x – k = 0 is \(\frac{2}{3}\)
Statement (B) : The quadratic equation ax2 + bx + c = 0, a ≠ 0 has two roots.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)
Explanation:
As one root is \(\frac{2}{3}\) ⇒ x = \(\frac{2}{3}\)
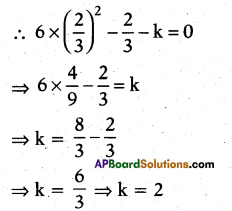
So, both A and B are correct but B does not explain Answer:
∴ Hence, (i) is the correct option.
Question 141.
Statement (A) : The equation 8x2 + 3kx + 2 = 0 has equal roots, then the value of k is ± \(\frac{8}{3}\).
Statement (B) : The equation ax2 + bx + c = 0 has equal roots if D = b2 – 4ac = 0.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)
Explanation:
8x2 + 3kx + 2 = 0
∴ Discriminant, D = b2 – 4ac
= (3k)2 – 4 x 8 x 2
= 9k2 – 64
For equal roots, D = 0
⇒ 9k2 – 64 = 0
⇒ 9k2 = 64
⇒ k2 = \(\frac { 64 }{ 9 }\)
⇒ 9k2 = ±\(\frac { 8 }{ 3 }\)
So, A and B both correct and B explains Answer: Hence, (i) is the correct option.
Question 142.
Statement (A) : The values of x are \(\frac{-a}{2}\), a for a quadratic equation 2x2 + ax – a2 = 0.
Statement (B) : For quadratic equation ax2 + bx + c = 0.
x = \(\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(iii)
Explanation:
2x2 + ax – a2 =0

So, A is incorrect but B is correct. Hence, (iii) is the correct option.
Question 143.
Statement (A) : The equation (x – p) (x – r) + λ(x – q) (x – s) = 0, p < q < r < s, has non-real roots if λ > 0.
Statement (B) : The equation ax2 + bx + c = 0, a, b,c ∈ R, has non-real roots if b2 – 4ac < 0.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(iii)
Explanation:
Statement (A):
Let f(x) = (x – p) (x – r) + λ(x – q) (x- s)
f(p) = λ(p – q) (p – s)
f(q) = (q – p) (q – r)
f(s) = (s – p) (s – r)
f(r) = λ(r – q) (r – s)
If λ > 0, then f(p) > 0, f(q) < 0, f(r) < 0 and f(s) > 0.
⇒ f(x) = 0 has one real root between p and q and other real root between r and s.
Statement – B is obviously true. Option (iii) is correct.
Question 144.
Statement (A) : If roots of the equation x2 – bx + c = 0 are two consecutive integers, then b2 – 4c = 1.
Statement (B) : If a, b, c are odd integer, then the roots of the equation 4abc x2 + (b2 – 4ac)x – b = 0 are real and distinct.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(ii)
Explanation:
Statement (A) : Given equation , x2 – bx + c = 0.
Let α, β be two roots such that |α – β| = 1. .
⇒ (α + β)2 – 4αβ = 1.
⇒ b2 – 4c = 1
Statement (B): Given equation
4abc x2 + (b2 – 4ac) x – b = 0
D = (b2 – 4ac)2 + 16 ab2 c
D = (b2 – 4ac)2 > 0
Hence roots are real and unequal. Option (ii) is correct.
Question 145.
Statement (A) : If 1 ≤ a ≤ 2, then \(\sqrt{a+2 \sqrt{a-1}}+\sqrt{a-2 \sqrt{a-1}}=2\)
Statement (B) : If 1 ≤ a ≤ 2, then (a – 1) > 1.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(ii)
Explanation:
If 1 ≤ a ≤ 2 ⇒ 0 ≤ a- 1 ≤ 1
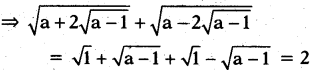
Statement – A is true.
Statement – B is false.
Option – (ii) is correct.
![]()
Question 146.
Statement (A): If one root is \(\sqrt{3}-\sqrt{2}\), then the equation of lowest degree with rational coefficients x4 – 10x2 + 1 = 0.
Statement (B): For a polynomial equa-tion with rational coefficient irrational roots occurs in pairs.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)
Explanation:
x = \(\sqrt{3}-\sqrt{2}\), x2 = 5 – 2\(\sqrt{6}\)
(x2 – 5)2 = 24
x4 – 10x2 + 25 = 24
x4 – 10x2 + 1 = 0
For polynomial equation with rational coefficients irrational roots occurs in pairs.
Option (i) is correct.
Question 147.
Statement (A): Degree of the polynomial 5x2 + 3x + 4 is 2.
Statement (B) : The degree of a poly-nomial of one variable is the highest value of the exponent of the variable.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)
Read the below passages and answer to the following questions.
Let us consider a quadratic equation x2 + 3ax + 2a2 = 0.
If the above equation has roots α,β and it is given that α2 + β2 = 5.
Question 148.
Find value of ‘a’.
Answer:
±1.
Explanation:
α + β = – 3a; αβ = 2a2
a2 + p2 = 5
⇒ (α + β)2 – 2αβ = 5
⇒ (- 3a)2 – 2(2a2) = 5
⇒ 9a2 – 4a2 = 5
⇒ 5a2 = 5 ⇒ a = ± 1
Question 149.
Find value of ‘D’ for the above qua-dratic equation.
Answer:
D > 0.
Explanation:
D = (3a)2 – 4(2a2)
= 9a2 – 8a2 = a2 = 1 > 0
Question 150.
Find the product of roots.
Answer:
2
Explanation:
αβ = 2a2 = 2(1) = 2
Let us consider a quadratic equation x2 + λx + λ + 1.25 = O, where λ is a constant. The value of A such that the above quadratic equation has
Question 151.
Two distinct roots.
Answer:
λ > 5 or λ < – 1.
Explanation:
The equation has two distinct roots if b2 – 4ac > 0.
∴ (λ – 5)(λ + 1) > 0
⇒ Either λ – 5 > 0 (or) λ + 1 > 0
⇒ λ > 5 (or) λ > -1
∴ λ > 5
⇒ λ – 5 <0 (or) λ + 1 < 0
⇒ λ < 5 (or) λ < – 1
∴ λ < -1 Hence the given equation has two dis-tinct roots for λ > 5 (or) λ < – 1
Question 152.
Two coincident roots.
Answer:
λ = 5 or λ = -1.
Explanation:
The equation has two coincident roots if b2 – 4ac = 0
⇒ (λ – 5) (λ + 1) = 0
⇒ Either λ – 5 = 0 (or) λ = 5
⇒ λ + 1 = 0
⇒ λ = – 1
⇒ λ = 5 or – 1
Hence the given equation has coincident roots for λ = 5 or – 1.
The area of a rectangular plot is 528 m2. The length of the plot is one more than twice its breadth.
Question 153.
Which mathematical concept is used to find area of above plot ?
Answer:
Quadratic equation.
Question 154.
Write the breadth and length of above given plot.
Answer:
Let breadth = x m, length = 2x + 1 m.
Question 155.
Write the equation of area of above given plot.
Answer:
Area = length x breadth
= x(2x + 1) – 2x2 + x = 528 m2.
The hypotenuse of a right triangle is 25 cm. We know that the difference in lengthof the other two sides is 5 cm.
Question 156.
Write the lengths of smaller and larger sides.
Answer:
Smaller side = x m
Larger side = (x + 5) cm.
Question 157.
Write the hypotenuse of the triangle.
Answer:
x2 + (x + 5)2 = (25)2
i.e., x2 + 5x – 300 = 0
![]()
Question 158.
Which mathematical concept is used to find out the values of dimensions ?
Answer:
Quadratic equations.
Question 159.
Column -II give roots of quadratic equations given in column – I, match them correctly.

Answer:
A – (iv), B – (ii).
Question 160.
Column – II give roots of quadratic equations given in column -1, match them correctly.

Answer:
A – (i), B – (iii).
Question 161.
Write the correct matching.

Answer:
A – (ii), B – (iv).
Question 162.
Write die correct matching.

Answer:
A – (iii), B – (i).
Question 163.
Column – II give pair at two numbers for solution to problems given in column -I. Match them correctly.
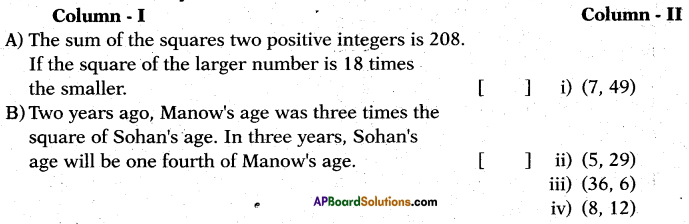
Answer:
A – (iv), B – (ii).
Question 164.
Column – II give pair at two numbers for solution to problems given in column -I.
Match them correctly.

Answer:
A – (i), B – (iii).
Question 165.
D is the discriminait of the quadratic equation ax2 + bx + e = 0.
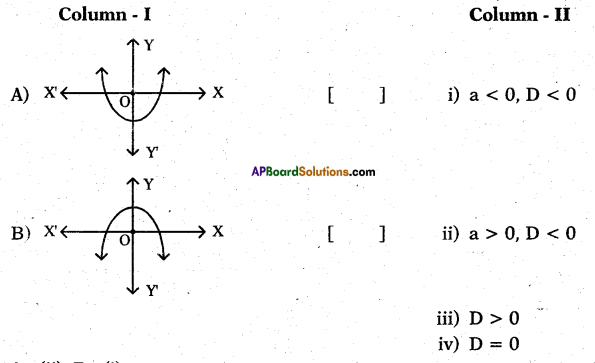
Answer:
A – (ii), B – (i).
Question 166.
D Is the discriminant of the quadratic equation ax2 + bx + c = O.
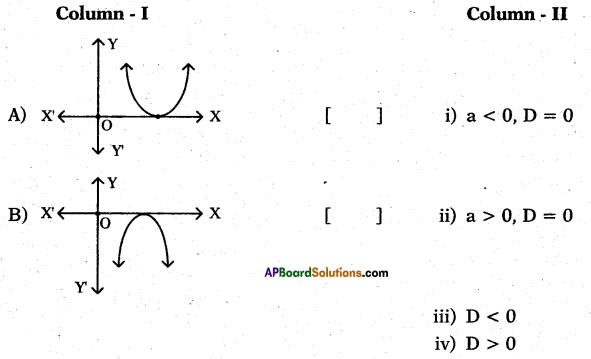
Answer:
A – (ii), B – (i).
Question 167.
Write a quadratic equation with roots 3 and 4.
Answer:
x2 – 7x + 12 = 0
Question 168.
Draw the rough graph of the quadratic equation ax2 + bx + c = 0, when b2 – 4ac < 0.
Answer:
