TS 10th Class Maths Model Paper Set 9 with Solutions

The strategic use of TS 10th Class Maths Model Papers Set 9 can significantly enhance a student’s problem-solving skills.

TS SSC Maths Model Paper Set 9 with Solutions

Time: 3 Hours
Maximum Marks: 80

General Instructions:

1. Answer all the questions under Part – A on a separate answer book.
2. Write the answers to the questions under Part – B on the question paper itself and attach it to the answer book of Part – A.

Part – A (60 Marks)
Section – I (6 × 2 = 12 Marks)

Note :

1. Answer ALL the following questions,
2. Each question carries 2 marks.

Question 1.
Find, the values of k for which the quadratic equation 4x² + 5kx + 25 = 0 has equal roots.
Answer:
Comparing the given quadratic equation
4x² + 5kx + 25 = 0
with ax² + bx + c = 0, we get
a = 4, b = 5k, c = 25
It is given that Q.E has equal roots
b² – 4ac = 0
⇒ (5k)² – 4(4) (25) = 0
⇒ 25k² – 400 = 0 ⇒ 25k² = 400
⇒ k² = \(\frac{400}{25}\) = 16
∴ k = \(\sqrt{16}\) = ± 4

Question 2.
Find the value of log_√2 128.
Answer:

Question 3.
For the A.P. ; -3, -7, -11, …………. ; can we find directly a₃₀ – a₂₀ without actually finding a₃₀ and a₂₀.
Answer:
Given A.P is -3, -7, -11, …………….
Here a = -3 and d = a₂ – a₁ = -7 – (-3) = -4
Now, we have the formula
a_n = a + (n – 1) d
∴ a₃₀ – a₂₀ = (a + 29d) – (a + 19d)
= a + 29d – a – 19d
= 10d
= 10 × -4 = -40
Yes, we can find directly a₃₀ – a₂₀ without finding a₃₀ and a₂₀.

Question 4.
When a dice is rolled, find the probability of getting odd prime number.
Answer:
When a dice is rolled,
The probability of getting odd prime number
= \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\) = \(\frac{2}{6}\) = \(\frac{1}{3}\)

Question 5.
Prove that 4tan² 45° – cosec² 30° + cos² 30° = \(\frac{3}{4}\).
Answer:
LHS = 4 tan²45° – cosec²30° + cos²30°
= 4(1)² – (2)² + (\(\frac{\sqrt{3}}{2}\))²
= 4 – 4 + \(\frac{3}{4}\) = \(\frac{3}{4}\) = RHS
∴ LHS = RHS

Question 6.
Find the mean of prime numbers which are less than 30.
Answer:
Prime numbers that are less than 30 are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29
Their mean = \(\frac{\text { Sum of observations }}{\text { number of observations }}\)
= \(\frac{2+3+5+7+11+13+17+19+23+29}{10}\)
= \(\frac{129}{10}\) = 12.9

Section – II (6 × 4 = 24 Marks)

Note :

1. Answer ALL the following questions.
2. Each question carries 4 marks.

Question 7.
If A = {1, 2, 3, 4,} B = {2, 4, 6, 8,10}, then represent the Venn diagram of A – B.
Answer:
Given A = {1, 2, 3, 4}, B = {2,4,6,8,10}
Venn – Euler diagram

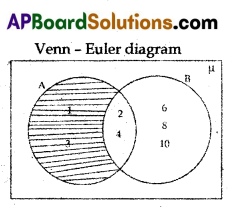
A – B = {1, 3}

Question 8.
If one of the zeroes of the cubic polynomial p(x) = ax³ + bx² + cx + d is zero, then find the product of other two zeroes of p(x). (a ≠ 0)
Answer:
p(x) = ax³ + bx² + cx + d
Let α, β, γ be the zeroes of p(x)
It is given one of the zeroes say γ = 0
we have αβ + βγ + γα = \(\frac{\mathrm{c}}{\mathrm{a}}\)
αβ + β(0) + 0(α) = \(\frac{\mathrm{c}}{\mathrm{a}}\)
αβ + 0 + 0 = \(\frac{\mathrm{c}}{\mathrm{a}}\)
αβ = \(\frac{\mathrm{c}}{\mathrm{a}}\) [∵ γ = 0]
Thus the product of the remaining two zeroes = \(\frac{\mathrm{c}}{\mathrm{a}}\)

Question 9.
Lalitha says that HCF and LCM of the numbers 80 and 60 are 20 and 120 respectively. Do you agree with her ? Justify.
Answer:
We know that
LCM × HCF = Product of two numbers
⇒ 20 × 120 = 80 × 60
⇒ 2400 = 4800 which is not true
∴ I don’t agree with Lalitha.

Question 10.
If cosec (A + B) = -1 and cot (A – B) = √3 0° < A + B ≤ 90°, A > B then find A and B.
Answer:
Suppose cosec (A + B) = 1
but cosec (90°) = 1
∴ cosec (A + B) = cosec 90°
Since 0° < A + B < 90°, we get
A + B = 90° ……………. (1)
Also, cot (A – B) = √3
but cot 30° = √3
cot (A – B) = cos 30°
since A – B is also acute,
A – B = 30° ………… (2)
adding (1) and (2),
A + B + A – B = 90° + 30°
2A = 120°
A = \(\frac{120}{2}\) = 60°
From (1), we get 60° + B = 90°
B = 90° – 60° – 30°
∴ A = 60°, B = 30°

Question 11.
A bag contains 7 red, 5 white and 6 black balls. A, ball is drawn from the bag at random, find the probability that the ball drawn is not black.
Answer:
A bag contains 7 red, 5 white and 6 black balls. Total number of possible outcomes
The number of favourable outcomes when the drawn ball is not black = 7 + 5 = 12.
∴ The probability that the ball drawn is not black
= \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{12}{18}\) = \(\frac{2}{3}\)

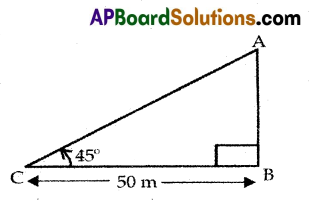
Question 12.
The angle of elevation of the top of a tower from a point on the ground which is 50 m away from the
foot of the tower is 45°. Draw the diagram for the situation.
Answer:

Section – III (4 × 6 = 24 Marks)

Note :

1. Answer any 4 of the following questions.
2. Each question carries 6 marks.

Question 13.
The below distribution gives the weight of 40 students in a class. Find the median weight of the students.

Answer:

Weight (in kg)	Number of students	LCF
30 – 35	4	4
35 – 40	5	9
40 – 45	10	19 cf
45 – 50	8(f)	27 median
50 – 55	8	35
55 – 60	5	40(n)

Here, \(\frac{n}{2}\) = \(\frac{40}{2}\) = 20 ; median class = (45 – 50) ; l = 45, f = 8, cf = 19, h = 5
Median = l + \(\left[\frac{\mathrm{n}-\mathrm{cf}}{\mathrm{f}}\right]\) × h = 45 + (\(\frac{20-19}{8}\)) × 5 = 45 + \(\frac{5}{8}\) = 45 + 0.625 = 45.625

Question 14.
Prove that the parallelogram circumscribing a circle is a rhombus.
Answer:

Given : ABCD is a parallelogram circumscribing a circle.
Proof : ABCD is a rhombus.
To prove : ABCD is a parallelogram
AB = CD and AD = BC ……… (1)
The lengths of tangents to a circle from an external point are equal.
Thus,
AS = AP; BQ = BP; CQ – CR;
DS = RD
By adding we get
AS + BQ + CQ + DS
= AP + BP + CR + RD
AS + DS + BQ + CQ
= AP + BP + CR + RD
AD + BC = AB + CD.
From (1), We have
AD + AD = AB + AB
2 AD = 2 AB
AD = AB ………… (2)
From (1) and (2), we conclude that
AB = BC = CD = AD
∴ ABCD is a rhombus.
Hence proved.

Question 15.
The base of a triangle is 4 cm longer than its altitude. If tire area of die triangle is 48 sq. cm then find its base and altitude.
Answer:
Let the altitude of a triangle be x cm
Its base = (x + 4) cm
Area of the triangle = \(\frac{1}{2}\) × base × altitude
= \(\frac{1}{2}\) × x × (x + 4)
= \(\frac{1}{2}\)(x² + 4x)sq.cm
Given the area of the triangle = 48 sq.cm.
\(\frac{1}{2}\)(x² + 4x) = 48
x² + 4x = 48 × 2
x² + 4x = 96 ⇒ x² + 4x – 96 = 0
x² + 12x – 8x -96
(x + 12)(x – 8) = 0
Either x + 12 = 0 or x – 8 = 0
x + 12 = 0 gives x = -12
x – 8 = 0 gives x = 8
x = -12 is not possible
∴ Altitude = x = 8cm
∴ Base= x + 4 = 8 + 4 = 12 cm
Base = 12 cm : Altitude = 8 cm

Question 16.
Sum of the squares of two consecutive positive even integers is 100; find those numbers by using quadratic equations.
Answer:
Let x and x + 2 be die two consecutive positive even integers.
x² + (x + 2 )² = 100
after simplifications, x² + 2x – 48 = 0
(x + 8) (x – 6) = 0
x = -8 or x = 6
∴ The two consecutive positive even integers are 6 and 8

Question 17.
Solve the following pair of linear equations by graph method. 2x + y = 6 and 2x – y + 2 = 0
Answer:
Given pair of linear equations is 2x + y = 6 and 2x – y + 2 = 0
2x + y = 6

x	0	1	2
y	6	4	2
(x, y)	(0, 6)	(1, 4)	(2, 2)

2x – y + 2 = 0

x	0	1	2
y	2	4	6
(x, y)	(0, 2)	(1, 4)	(2, 6)

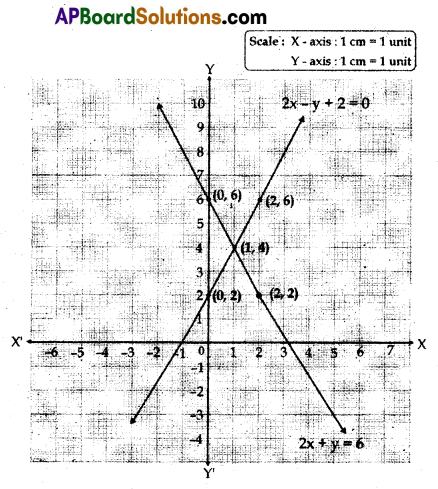
From the graph, the two straight lines represented by given equations intersect at the point (1, 4) ∴ The solution of the given pair of linear equations is x = 1, y = 4.

Question 18.
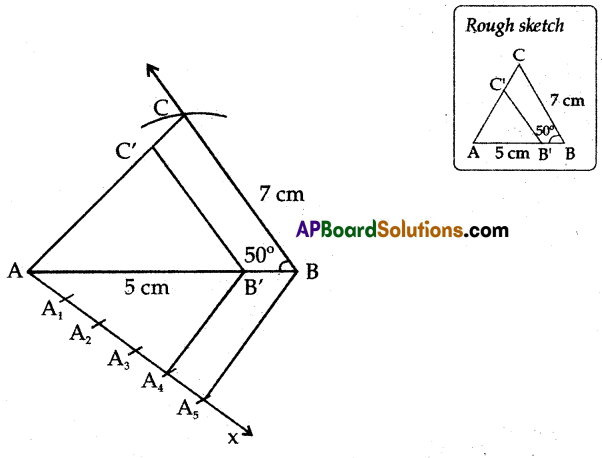
Construct a triangle ABC in which AB = 5 cm, BC = 7 cm and ∠ABC = 50°, then construct a triangle similar to it, whose sides are \(\frac{4}{5}\) of the corresponding sides of first triangle.
Answer:
Steps of construction:

1. Draw a triangle ABC with
   AB = 5cm, BC = 7 cm and ∠ABC = 50°
2. Draw a ray \(\overrightarrow{\mathrm{AX}}\) such that ∠BAX is an acute angled
3. Draw A₁, A₂, A₃, A₄, A₅ arcs on \(\overrightarrow{\mathrm{AX}}\) such that AA₁ = A₁A₂ = …………. = A₄A₅
4. Join A₅ and B.
5. Draw a parallel line to A₅B through A₄ to meet AB at B’
6. Draw a parallel line to BC through B’ to meet AC at C’
7. ΔAB’C’ is the required similar triangle.
   

Part – B (20 Marks)

Note :

1. Answer all the questions,
2. Each question carries 1 mark,
3. Answers are to be written in Question paper only,
4. Marks will not be awarded in any case of over writing, rewriting or erased answers.

Note : Write the capital letters (A, B, C, D) showing the correct answer for the following questions in the brackets provided against them.

Question 1.
If set A and set B are disjoint sets and n(A) = 6, n(B) = 5, then n(A∪B)
A) 11
B) 6
C) 5
D) 1
Answer:
A) 11

Question 2.
The decimal expansion of 0.225 in its rational form is
A) 225
B) \(\frac{225}{10^2}\)
C) \(\frac{225}{10^4}\)
D) \(\frac{1}{2}\)
Answer:
D) \(\frac{1}{2}\)

Question 3.
If p(x) = x² – 4x + 5, then the value of p(1) is
A) -1
B) 0
C) 1
D) 2
Answer:
D) 2

Question 4.
If 2x + 3y = 8 and 4x + py = 16 has infinite solutions, then p = ……………
A) 8
B) 6
C) 10
D) 16
Answer:
B) 6

Question 5.
From the graph, the zeroes of the polynomial are …………..

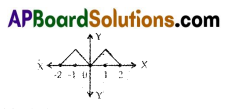
A) -2
B) 0
C) 2
D) -2, 0, 2
Answer:
D) -2, 0, 2

Question 6.
Every even positive integer can be written in the form of ………………
A) 2p + 1 (p ∈ Z⁺)
B) 2p – 1 (p ∈ Z⁺)
C) 2p (p ∈ Z⁺)
D) 3p (p ∈ Z⁺)
Answer:
C) 2p (p ∈ Z⁺)

Question 7.
Which of the following is true ?
A) Φ = 0
B) Φ = {}
C) Φ = {0}
D) Φ = {1}
Answer:
B) Φ = {}

Question 8.
Sum of the first 10 natural numbers is
A) \(\frac{10 \times 9}{2}\)
B) \(\frac{10 \times 10}{2}\)
C) \(\frac{10 \times 11}{2}\)
D) \(\frac{10 \times 100}{2}\)
Answer:
C) \(\frac{10 \times 11}{2}\)

Question 9.
What does ‘r’ represent in the general term of GP, a_n = ar^n-1
A) Radius
B) Common ratio
C) Common difference
D) Common multiple
Answer:
B) Common ratio

Question 10.
If slope of a line is ‘1’, then the angle between the line and X – axis is
A) 45°
B) 30°
C) 60°
D) 90°
Answer:
A) 45°

Question 11.
From a set of single digit natural numbers, if a number chosen at random, then the probability that the number chosen is a multiple of 2, is
A) \(\frac{4}{9}\)
B) \(\frac{1}{3}\)
C) \(\frac{9}{4}\)
D) \(\frac{2}{5}\)
Answer:
A) \(\frac{4}{9}\)

Question 12.
2 – 2 sin² 60° =
A) sin 60°
B) tan 60°
C) cos 60°
D) sec 60°
Answer:
C) cos 60°

Question 13.
If 14 is deleted from the data 12, 14, 15, 16, 17, 18, 19 and 20, then the median increases by
A) 1
B) 1.5
C) 2
D) 0.5
Answer:
D) 0.5

Question 14.
The mean of the first eight multiples of 3 is
A) 8
B) 13.5
C) 13
D) 27
Answer:
B) 13.5

Question 15.
If P(E) the probability of an event, then
A) P(E) ≥ 1
B) P(E) ≤ 0
C) 0 ≤ P(E) ≤ 1
D) P(E) ≤ 1
Answer:
C) 0 ≤ P(E) ≤ 1

Question 16.
From the given figure, ∠XOY = 130°, then ∠XPO =

A) 65°
B) 35°
C) 25°
D) 55°
Answer:
C) 25°

Question 17.
The value of cos 15° × cos 45° × 2cosec 75° is
A) \(\frac{2}{\sqrt{3}}\)
B) \(\frac{\sqrt{3}}{2}\)
C) \(\frac{1}{\sqrt{3}}\)
D) 2
Answer:
D) 2

Question 18.
The volume of a cylinder is given by the formula πr²h, here “h” represents
A) diameter
B) height
C) radius
D) slant height
Answer:
B) height

Question 19.
ΔABC ~ ΔXYZ, AB : XY = 9 : 16,then ar (ΔABC) : ar (ΔXYZ) is
A) 3 : 4
B) 4 : 3
C) 81 : 256
D) 256 : 81
Answer:
C) 81 : 256

Question 20.
In the given figure, DE || BC, if \(\frac{\mathrm{AD}}{\mathrm{DB}}\) = \(\frac{3}{2}\) and EC = 3.6 cm, then AE =

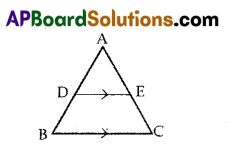
A) 4.5 cm
B) 5.6 cm
C) 5.4 cm
D) 4.6 cm
Answer:
C) 5.4 cm