TS 10th Class Maths Model Paper Set 8 with Solutions

The strategic use of TS 10th Class Maths Model Papers Set 8 can significantly enhance a student’s problem-solving skills.

TS SSC Maths Model Paper Set 8 with Solutions

Time: 3 Hours
Maximum Marks: 80

General Instructions:

1. Answer all the questions under Part – A on a separate answer book.
2. Write the answers to the questions under Part – B on the question paper itself and attach it to the answer book of Part – A.

Part – A (60 Marks)
Section – I (6 × 2 = 12 Marks)

Note :

1. Answer ALL the following questions,
2. Each question carries 2 marks.

Question 1.
Find the value of k, if 2 is one of the roots of the quadratic equation x² – kx + 6 = 0
Answer:
x² – kx + 6 = 0
(2)² – k(2) + 6 = 0
4 + 6 – 2k = 0
2k = 10 ⇒ k = 5

Question 2.
In a rectangle ABCD,
AB = x + y, BC = x – y,
CD = 9 and AD = 3.

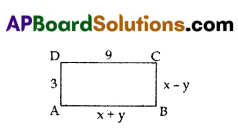
Find the values of x and y.
Answer:
x + y = 9

{∵ two pairs of opposite sides are equal, in a rectangle.}
x – y = 3.
Solving the above equations, we get x = 6 and y = 3.

Question 3.
If the slope of the line passing through the two points (2, 5) and (5, 8) is represented by tan θ; (where 0° < θ < 90°) in trigonometry, then find angle ‘θ’.
Answer:
Points on the given line are (2, 5) and (5, 8)
Slope = Tan θ = \(\frac{y_2-y_1}{x_2-x_1}\)
Tan θ = \(\frac{8-5}{5-2}\) = \(\frac{1}{2}\) = 1 ⇒ Tan 45°
∴ θ = 45° ( ∵ 0° < θ < 90°)

Question 4.
It is given that ΔABC ~ ΔDEF. Is it true to say that = \(\frac{\mathrm{BC}}{\mathrm{DE}}=\frac{\mathrm{AB}}{\mathrm{EF}}\) Justify your answer.
Answer:
Given that ΔABC ~ ΔDEF
∴ \(\frac{\mathrm{AB}}{\mathrm{DE}}\) = \(\frac{\mathrm{BC}}{\mathrm{EF}}\) = \(\frac{\mathrm{AC}}{\mathrm{DF}}\)
[∵ Ratio of corresponding sides of similar triangles are equal]
But \(\frac{\mathrm{BC}}{\mathrm{DE}}\) = ‘\(\frac{\mathrm{AB}}{\mathrm{EF}}\) (given)
∴ Given statement is wrong.

Question 5.
Evaluate : \(\frac{{Sin} 58^{\circ}}{{Cos} 32^{\circ}}+\frac{{Tan} 42^{\circ}}{{Cot} 48^{\circ}}\).
Answer:
\(\frac{{Sin} 58^{\circ}}{{Cos} 32^{\circ}}+\frac{{Tan} 42^{\circ}}{{Cot} 48^{\circ}}\) = \(\frac{{Sin} 58^{\circ}}{{Cos}(90-58)^{\circ}}+\frac{{Tan} 42^{\circ}}{{Cot}(90-42)^{\circ}}\)
= \(\frac{{Sin} 58^{\circ}}{{Sin} 58^{\circ}}+\frac{{Tan} 42^{\circ}}{{Tan} 42^{\circ}}\) = 1 + 1 = 2

Question 6.
Write the formula to find the mean of a grouped data, using assumed mean method and explain each term.
Answer:
Mean = a + \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{d}_{\mathrm{i}}}{\sum \mathrm{f}_{\mathrm{i}}}\)
a – assumed mean
f – frequency
d – x – a
x – class mark

Section – II (6 × 4 = 24 Marks)

Note :
(i) Answer ALL the following questions.
(ii) Each question carries 4 marks.

Question 7.
Show that 2 and – \(\frac{1}{3}\) are zeroes 04 the polynomial 3x² – 5x – 2.
Answer:
p(x) = 3×2 – 5x – 2
p(2) = 3(2)2 – 5(2) – 2
= 12 – 10 – 2
= 12 – 12 = 0
= p(-\(\frac{1}{3}\)) = 3(-\(\frac{1}{3}\))² – 5(-\(\frac{1}{3}\)) – 2
= \(\frac{1}{3}\) + \(\frac{5}{3}\) – 2
= 2 – 2 = 0
∴ 2 and –\(\frac{1}{3}\) are zeroes of p(x)

Question 8.
If the measure of angles of a triangle are x°, y° and 40°, and difference between the two measures of angles x° and y° is 30°, then find the values of x° and y°.
Answer:
x + y + 40 = 180°
(∵ sum of angles of a triangle is 180°)
x + y = 140 ……………. (1)
x – y = 30 …………… (2)
Solving the above equations we obtain x = 85°, y = 55°

Question 9.
Express 2016 as product of prime factors.
Answer:

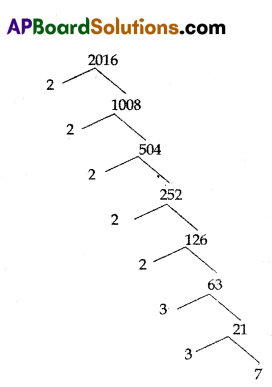
2016 = 2 × 2 × 2 × 2 × 2 × 3 × 3 × 7 = 2⁵ × 3² × 7

Question 10.
There are 5 red balls, 4 green balls and 6 yellow balls in a box. If a ball is selected at random, what is the probability of not getting a yellow ball ?
Answer:
Total no. of balls in a bag = 15
Total no. of chances to select a ball from the box = 15
Favourable outcomes to select not yellow ball = 9
Probability of not getting a yellow ball
= \(\frac{\text { No. of favourable outcomes }}{\text { Total no. of outcomes }}\) = \(\frac{9}{15}\) = \(\frac{3}{5}\)

Question 11.
A toy is in the form of a cone mounted on a hemisphere. The radius of the base and the height of the cone are 7 cm and 8 cm respectively. Find the surface area of the toy. (π = \(\frac{22}{7}\))
Answer:

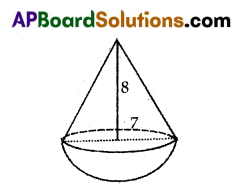
According to the data Radius of hemisphere = Radius of the base of cone = r
r = 7 cm.
Height of cone = h = 8 cm
Slant height of cone = l = \(\sqrt{\mathrm{r}^2+\mathrm{h}^2}\) = \(\sqrt{7^2+8^2}\) = \(\sqrt{49+64}\) = \(\sqrt{113}\)
Surface area of toy = Curved surface area of cone. + Surface area of hemisphere
= π rl + 2π r²
= \(\frac{22}{7}\) × 7 × \(\sqrt{113}\) + 2 × \(\frac{22}{7}\) × 7²
= 22\(\sqrt{113}\) + 308 sq. cm.

Question 12.
Draw a circle with 5 cm radius and construct a pair of tangents to the circle.
Answer:

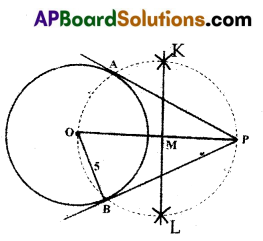
Section – III (4 × 6 = 24 Marks)

Note :

1. Answer any 4 of the following questions.
2. Each question carries 6 marks.

Question 13.
A tree is broken without separating from the stem by the wind. The top touches the ground making an angle 30° at a distance of 12 m from the foot of the tree. Find the height of the tree before breaking.
Answer:
Let height of the tree before broken = (x + y)m
According to the data Foot of the tree = A
Tree broken at B

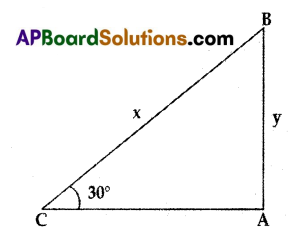
Top of the tree touches after broken at C
Given AC = 12 m. ∠ACB – 30°
tan 30° = \(\frac{y}{12}=\frac{1}{\sqrt{3}}=\frac{y}{12}\)
y = \(\frac{12}{\sqrt{3}}\) = 4√3m
cos 30° = \(\frac{12}{x}\)
\(\frac{\sqrt{3}}{2}=\frac{12}{x}\)
x = \(\frac{12 \times 2}{\sqrt{3}}\) = 8√3mt
Height of the tree before broken = x + y
= 8√3 + 4√3
= 12√3 m

Question 14.
Prove that √3 + √5 is an irrational number.
Answer:
√3 + √5
Let us suppose that √3 + √5 is rational
Let √3 + √5 = \(\frac{a}{b}\), where \(\frac{a}{b}\) is rational, b ≠ 0
∴ √3 = \(\frac{a}{b}\) – √5
Squaring on both sides, we get

Since a,b are integers \(\frac{a^2+2 b^2}{2 a b}\) is rational and so, √5 is rational
This contradicts the fact that √5 is irrational.
Hence √3 + √5 is irrational.

Question 15.
If the points P (-3, 9), Q (a, b) and R (4, -5) are collinear and a + b = 1, then find the values of a and b.
Answer:
Points P, Q, R are collinear
⇒ area of ΔPQR = 0
P(-3,9) Q (a, b) R(4, 5)
Area of triangle = \(\frac{1}{2}\) |x₁ (y₂ – y₃)
+ x₂ (y₃ – y₁) + x₃ (y₁ – y₂)|
0 = \(\frac{1}{2}\) | -3 (b + 5) + 4 (-5 -9) + (9 – b) |
After simplifications, we get
2a + b = 3 …………… (1)
given equation
a + b = 1 …………….. (2)
Solving equations (1) and (2),
we obtain a = 2 and b = -1

Question 16.
Two boys on either side of their school building of 20 m height observe its top at the angles of elevation 30° and 60° respectively. Find the distance between two boys.
Answer:

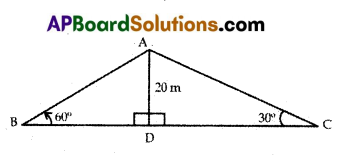
From the figure
AD = height of the building
= 20m
BC = Distance between two boys.
∠ABD = 60°, ∠ACD = 30°
In ΔABD,
cot 30° = \(\frac{\mathrm{BD}}{\mathrm{AD}}\)

Question 17.
Draw the graph for the equations 2x – y – 4 = 0 and x + y + 1 = 0 on the graph paper and check whether they are consistent or not.
Answer:
B) 2x – y – 4 = 0 …………. (1)
y = 2x – 4

x	0	1	2
2x	0	2	4
-4	-4	-4	-4
y	-4	-2	0
(x, y)	(0, -4)	(1, -2)	(2, 0)

x + y + 1 = 0 …………… (2)

x	0	1	2
-x	0.	-1	-2.
-1	-1	-1	-1
y	-1	-2	-3
(x, y)	(0, -1)	(1, -2)	(2, -3)

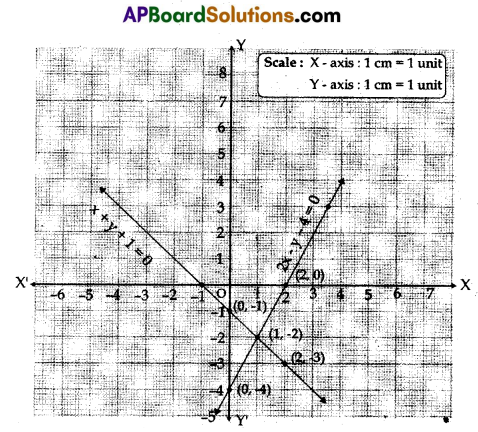
Intersecting point of equations (1) and (2) is (1, -2)
So x = 1, y = -2
∴ The given equations are consistent.

Question 18.
Construct a triangle of sides 5 cm, 6 cm and 7 cm. Then construct a triangle similar to it, whose sides are IV2 times the corresponding sides of the first triangle.
Answer:

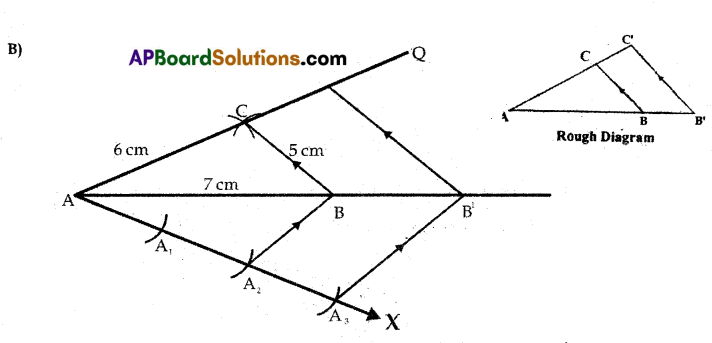
Steps of Construction :

1. Construct a triangle ABC with sides 5 cm, 6 cm and 7 cm.
2. Draw a ray AX making an acute angle with AB on the side opposite to vertex C.
3. Locate 3 points A₁, A₂, A₃ on AX. So that AA₁ = A₁A₂ = A₂A₃.
4. Join A₃B’ and draw a line from A₂ to B. Which is parallel.to A₃B’ and it is intersecting AB at B.
5. Draw a line through B parallel to B’C’ to intersect AC at AC’ So, AB’C is the required triangle.

Part – B (20 Marks)

Note :

1. Answer all the questions,
2. Each question carries 1 mark,
3. Answers are to be written in Question paper only,
4. Marks will not be awarded in any case of over writing, rewriting or erased answers.

Note : Write the capital letters (A, B, C, D) showing the correct answer for the following questions in the brackets provided against them.

Question 1.
The logarithmic form of a^b = c is ……………….
A) log_ac = b
B) log_b c = a
C) log_ab = c
D) log_ba = c
Answer:
A) log_ac = b

Question 2.
If 3 log (x +3) = log 27,.then the value of x is ………………….
A) 0
B) 1
C) 6
D) 24
Answer:
A) 0

Question 3.
In the formula of n^th term of a Geometric Progression, a_n = a. r^{n – 1}, r denotes ……………..
A) first term
B) common ratio
C) common difference
D) number of terms
Answer:
B) common ratio

Question 4.
Which one of the following rational numbers has terminating decimal expression?
A) \(\frac{11}{7000}\)
B) \(\frac{91}{21000}\)
C) \(\frac{343}{2^3 \times 5^3 \times 7^3}\)
D) \(\frac{21}{9000}\)
Answer:
C) \(\frac{343}{2^3 \times 5^3 \times 7^3}\)

Question 5.
The common difference of an Arithmetic Progression in which a₂₅ – a₁₂ = -52 is ……………..
A) 4
B) -4
C) -3
D) 3
Answer:
B) -4

Question 6.
Which one of the following statements is false?
A) Every set is subset of itself
B) Empty set is subset of every set
C) Intersection of two disjoint sets is empty set
D) Cardinal number of an infinite set is zero
Answer:
D) Cardinal number of an infinite set is zero

Question 7.
If the co-ordinates of the vertices of a rectangle are (0, 0), (4, 0), (4, 3) and (0, 3), then the length of its diagonal is
A) 4
B) 5
C) 7
D) 3
Answer:
B) 5

Question 8.
The quadratic polynomial having \(\frac{1}{3}\) and \(\frac{1}{2}\) as its zeroes, is ……………….
A) x² + \(\frac{5 x+1}{6}\)
B) -6x² – 5x + 1
C) x² – \(\frac{5 x-1}{6}\)
D) 6x² – 5x – 1
Answer:
C) x² – \(\frac{5 x-1}{6}\)

Question 9.
Sum of 10 terms of the progression log 2 + log 4 + log 8 + log 16 + ……………… is ……………
A) 45 log 2
B) 90 log 2
C) 10 log 2
D) 55 log 2
Answer:
D) 55 log 2

Question 10.
Which term of the Arithmetic Progression 24, 21, 18, ……………. is the first negative term ?
A) 8^th
B) 9^th
C) 10^th
D) 12^th
Answer:
C) 10^th

Question 11.
The value of Tan θ in terms of Cosec θ is ………………..
A) \(\frac{1}{\sqrt{{cosec}^2 \theta-1}}\)
B) \(\frac{{cosec} \theta}{\sqrt{{cosec}^2 \theta-1}}\)
C) \(\frac{2 {Cosec} \theta}{\sqrt{{cosec}^2 \theta-1}}\)
D) \(\frac{2}{\sqrt{{cosec}^2 \theta-1}}\)
Answer:
A) \(\frac{1}{\sqrt{{cosec}^2 \theta-1}}\)

Question 12.
Observe the following:
I) Sin² 20° + Sin² 70° = 1 II) Log₂ (Sin 90°)= 1 Which one is CORRECT ?
A) (I) only
B) (II) only
C) Both (I) and (II)
D) Neither (I) nor (II)
Answer:
A) (I) only

Question 13.
In ΔABC, AC = 12 cm, AB = 5 cm and ∠BAC = 30°, the area of ΔABC is
A) 30 cm²
B) 15 cm²
C) 60 cm²
D) 20 cm²
Answer:
B) 15 cm²

Question 14.
Which one of the following cannot be the probability of an event ?
A) \(\frac{2}{3}\)
B) \(\frac{4}{5}\)
C) 0.7
D) \(\frac{5}{4}\)
Answer:
D) \(\frac{5}{4}\)

Question 15.
The X – coordinate of the point of intersection of the two ogives of grouped data is ……………….
A) median of the data
B) mode of the data
C) mean of the data
D) average of mid values of the data
Answer:
A) median of the data

Question 16.
Volumes of two spheres are in the ratio of 8 : 27, the ratio of their surface areas is ………………
A) 2 : 3
B) 4 : 3
C) 2 : 9
D) 4 : 9
Answer:
D) 4 : 9

Question 17.
A solid ball is exactly fitted inside the cubical box of side ‘a’. The volume of the ball is
A) \(\frac{1}{3}\)π a³
B) \(\frac{1}{6}\)π a³
C) \(\frac{4}{3}\)π a³
D) \(\frac{8}{3}\)π a³
Answer:
B) \(\frac{1}{6}\)π a³

Question 18.
Express ‘x’ in terms of a, b and c in the following figure.

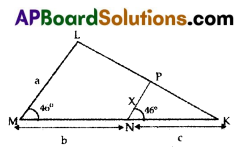
A) x = \(\frac{a c}{b+c}\)
B) x = \(\frac{b c}{b+c}\)
C) x = \(\frac{b+c}{a c}\)
D) x = \(\frac{a b}{a+c}\)
Answer:
A) x = \(\frac{a c}{b+c}\)

Question 19.
If the angle of elevation of sun increases from 0° to 90°, then the length of shadow of the tower ………………
A) no change
B) increases
C) decreases
D) can’t be decided
Answer:
C) decreases

Question 20.
In a right angled triangle with integral sides at least one of its measurements must be ……………..
A) multiples of 3 and 2
B) multiple of 9
C) multiples of 8
D) multiple of 7
Answer:
A) multiples of 3 and 2