AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 9 Tangents and Secants to a Circle Ex 9.1 Textbook Questions and Answers.
AP State Syllabus SSC 10th Class Maths Solutions 9th Lesson Tangents and Secants to a Circle Exercise 9.1
10th Class Maths 9th Lesson Tangents and Secants to a Circle Ex 9.1 Textbook Questions and Answers
Question 1.
Fill in the blanks.
i) A tangent to a circle intersects it in ——— point(s). (one)
ii) A line intersecting a circle in two points is called a ———. (secant)
iii) The number of tangents drawn at the end of the diameter is ———. (two)
iv) The common point of a tangent to a circle and the circle is called ———. (point of contact)
v) We can draw ——— tangents to a given circle. (infinite)
![]()
Question 2.
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Find length of PQ.
Answer:
Given: A circle with centre O and radius OP = 5 cm
\(\overline{\mathrm{PQ}}\) is a tangent and OQ = 12 cm
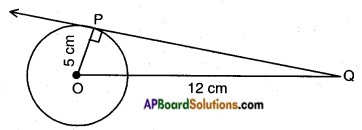 We know that ∠OPQ = 90°
We know that ∠OPQ = 90°
Hence in △OPQ
OQ2 = OP2 + PQ2
[∵ hypotenuse2 = Adj. side2 + Opp. side2]
122 = 52 + PQ2
∴ PQ2 = 144 – 25 .
PQ2 = 119
PQ = √119
Question 3.
Draw a circle and two lines parallel to a given line such that one is a tangent and the other, a secant to the circle.
Answer:
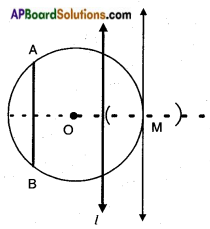 Steps:
Steps:
- Draw a circle with some radius.
- Draw a chord of the circle.
- Draw a line parallel to the chord intersecting the circle at two distinct points.
- This is secant of the circle (l).
- Draw another line parallel to the chord, just touching the circle at one point (M). This is a tangent of the circle.
![]()
Question 4.
Calculate the length of tangent from a point 15 cm. away from the centre of a circle of radius 9 cm.
Answer:
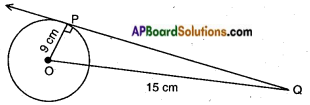 Given: A circle with radius OP = 9 cm
Given: A circle with radius OP = 9 cm
A tangent PQ from a point Q at a distance of 15 cm from the centre, i.e., OQ =15 cm
Now in △POQ, ∠P = 90°
OP2 + PQ2 – OQ2
92 + PQ2 = 152
PQ2 = 152 – 92
PQ2 = 144
∴ PQ = √144 = 12 cm.
Hence the length of the tangent =12 cm.
Question 5.
Prove that the tangents to a circle at the end points of a diameter are parallel.
Answer:
A circle with a diameter AB.
PQ is a tangent drawn at A and RS is a tangent drawn at B.
R.T.P: PQ || RS.
Proof: Let ‘O’ be the centre of the circle then OA is radius and PQ is a tangent.
∴ OA ⊥ PQ ……….(1)
[∵ a tangent drawn at the end point of the radius is perpendicular to the radius]
Similarly, OB ⊥ RS ……….(2)
[∵ a tangent drawn at the end point of the radius is perpendicular to the radius]
But, OA and OB are the parts of AB.
i.e., AB ⊥ PQ and AB ⊥ RS.
∴ PQ || RS.
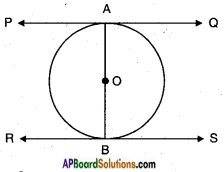 O is the centre, PQ is a tangent drawn at A.
O is the centre, PQ is a tangent drawn at A.
∠OAQ = 90°
Similarly, ∠OBS = 90°
∠OAQ + ∠OBS = 90° + 90° = 180°
∴ PQ || RS.
[∵ Sum of the consecutive interior angles is 180°, hence lines are parallel]
