AP SSC 10th Class Maths Solutions Chapter 10 Mensuration Ex 10.4

AP State Syllabus SSC 10th Class Maths Solutions 10th Lesson Mensuration Exercise 10.4

10th Class Maths 10th Lesson Mensuration Ex 10.4 Textbook Questions and Answers

Question 1.
A metallic sphere of radius 4.2 cm. is melted and recast into the shape of a cylinder of radius 6 cm. Find the height of the cylinder.
Answer:
Given, sphere converted into cylinder.
Hence volume of the sphere = volume of the cylinder.
Sphere:
Radius, r = 4.2 cm
Volume V = \(\frac{4}{3}\)πr³
= \(\frac{4}{3}\) × \(\frac{22}{7}\) × 4.2 × 4.2 × 4.2
= 4 × 22 × 0.2 × 4.2 × 4.2
= 4 x 22 x 0.2 x 4.2 x 4.2
= 310.464
Cylinder:
Radius, r = 6 cm
Height h = h say
Volume = πr²h
= \(\frac{22}{7}\) × 6 × 6 × h
= \(\frac{22 \times 36}{7} h\)
= \(\frac{792}{7} h\)
Hence, \(\frac{792}{7} h\) = 310.464
h = \(\frac{310.464 \times 7}{792}\) = 2.744cm
!! π can be cancelled on both sides i.e., sphere = cylinder

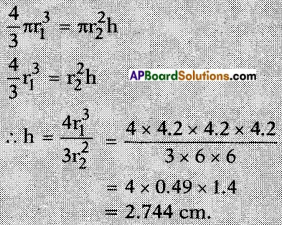
Question 2.
Three metallic spheres of radii 6 cm., 8 cm. and 10 cm. respectively are melted together to form a single solid sphere. Find the radius of the resulting sphere.
Answer:
Given : Radii of the three spheres r₁ = 6 cm r₂ = 8 cm r₃ = 10 cm
These three are melted to form a single sphere.
Let the radius of the resulting sphere be ‘r’.
Then volume of the resultant sphere = sum of the volumes of the three small spheres.


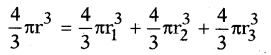
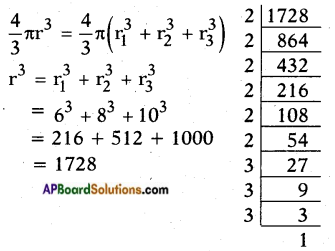
∴ 1728 = (2 × 2 × 3) × (2 × 2 × 3) × (2 × 2 × 3)
r³ = 12 × 12 × 12
r³ = 12³
∴ r = 12
Thus the radius of the resultant sphere = 12 cm

Question 3.
A 20 m deep well with diameter 7 m. is dug and the earth got by digging is evenly spread out to form a rectangu¬lar platform of base 22 m. × 14 m. Find the height of the platform.
Answer:
Volume of earth taken out = πr²h
= \(\frac{22}{7}\) × \(\frac{7}{2}\) × \(\frac{7}{2}\) × 20
= 770 m
Let height of plot form = H m.
∴ 22 × 14 × H = \(\frac{22}{7}\) × \(\frac{7}{2}\) × \(\frac{7}{2}\) × 20
H = \(\frac{35}{14}\) = \(\frac{5}{2}\) = \(2 \frac{1}{2} \mathrm{~m}\)
∴ The height of the plat form is \(2 \frac{1}{2} \mathrm{~m}\)

Question 4.
A well of diameter 14 m. is dug 15 m. deep. The earth taken out of it has been spread evenly all around it in the shape of a circular ring of width 7 m to form an embankment. Find the height of the embankment
Answer:
Volume of the well = Volume of the embank
Volume of the cylinder = Volume of the embank
Cylinder :
Radius r = \(\frac{d}{2}\) = \(\frac{14}{2}\) = 7 cm
Height/depth, h = 15 m
Volume V = πr²h
= \(\frac{22}{7}\) × 7 × 7 × 15
= 22 × 7 × 15
= 2310 m³
Embank:

Let the height of the embank = h m
Inner radius ‘r’ = Radius of well = 7 m
Outer radius, R = inner radius + width
= 7m + 7m = 14 m
Area of the base of the embank = (Area of outer circle) – (Area of inner circle)
= πR² – πr²
= π(R² – r²)
= \(\frac{22}{7}\)\(\left(14^{2}-7^{2}\right)\)
= \(\frac{22}{7}\) × (14+7) × (14-7)
= \(\frac{22}{7}\) × 21 × 7
= 462 m²
∴ Volume of the embank = Base area × height
= 462 × h = 462 h m³
∴ 462 h m³ = 2310 m³
h = \(\frac{2310}{462}\) = 5 m.

Question 5.
A container shaped like a right circular cylinder having diameter 12 cm. and height 15 cm. is full of ice-cream. The ice-cream is to be filled into cones of height 12 cm. and diameter 6 cm., having a hemispherical shape on the top. Find the number of such cones which can be filled with ice-cream.
Answer:
Let the number of cones that can be filled with the ice-cream be ‘n’.
Then total volume of all the cones with a hemi spherical top = Volume of the ice-cream

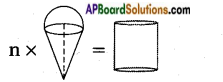
Ice-cream cone = Cone + Hemisphere = πr²h

Cone:
Radius = \(\frac{d}{2}\) = \(\frac{6}{2}\) = 3 cm
Height, h = 12 cm
Volume V = \(\frac{1}{3}\)πr²h
= \(\frac{1}{3}\) × \(\frac{22}{7}\) × 3 × 3 × 12
= \(\frac{22}{7}\) × 36
= \(\frac{792}{7}\)
Hemisphere:
Radius = \(\frac{d}{2}\) = \(\frac{6}{2}\) = 3 cm
Volume V = \(\frac{2}{3}\)πr³
= \(\frac{2}{3}\) × \(\frac{22}{7}\) × 3 × 3 × 3
= \(\frac{44 \times 9}{7}\)
= \(\frac{396}{7}\)
∴ Volume of each cone with ice-cream = \(\frac{792}{7}\) + \(\frac{396}{7}\) = \(\frac{1188}{7}\) cm³
Cylinder:
Radius = \(\frac{d}{2}\) = \(\frac{12}{2}\) = 6 cm
Height, h = 15 cm
Volume V = πr²h
= \(\frac{22}{7}\) × 6 × 6 × 15
= \(\frac{22 \times 36 \times 15}{7}\)
= \(\frac{11880}{7}\)
∴ \(\frac{11880}{7}\) = n × \(\frac{11880}{7}\)
⇒ n = \(\frac{11880}{7}\) × \(\frac{7}{1188}\) = 10
∴ n = 10.

Question 6.
How many silver coins, 1.75 cm in diameter and thickness 2 mm., need to be melted to form a cuboid of dimensions 5.5 cm × 10 cm × 3.5 cm?
Answer:
Let the number of silver coins needed to melt = n
Then total volume of n coins = volume of the cuboid
n × πr²h = lbh [∵ The shape of the coin is a cylinder and V = πr²h]

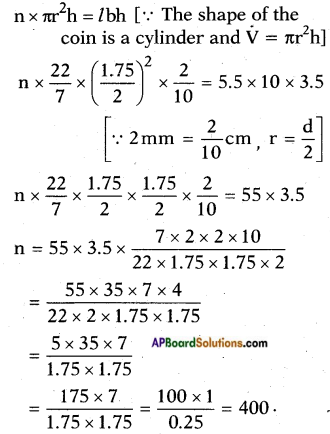
∴ 400 silver coins are needed.

Question 7.
A vessel is in the form of an inverted cone. Its height is 8 cm. and the radius of its top is 5 cm. It is filled with water up to the rim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped into the vessel, 1/4 of the water flows out. Find the number of lead shots dropped into the vessel.
Answer:

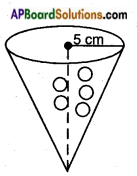
Let the number of lead shots dropped = n
Then total volume of n lead shots = \(\frac{1}{4}\) volume of the conical vessel.
Lead shots:
Radius, r = 0.5 cm
Volume V = \(\frac{4}{3}\)πr³
= \(\frac{4}{3}\) × \(\frac{22}{7}\) × 0.5 × 0.5 × 0.5
Total volume of n – shots
= n × \(\frac{4}{3}\) × \(\frac{22}{7}\) × 0.125
Cone:
Radius, r = 5 cm;
Height, h = 8 cm
Volume, V = \(\frac{1}{3}\) πr²h
= \(\frac{1}{3}\) × \(\frac{22}{7}\) × 5 × 5 × 8
= \(\frac{1}{3}\) × \(\frac{22}{7}\) × 200

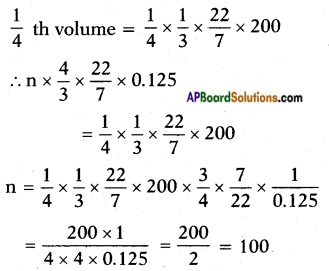
∴ Number of lead shots = 100.

Question 8.
A solid metallic sphere of diameter 28 cm is melted and recast into a number of smaller cones, each of diameter 4 \(\frac{d}{2}\) cm and height 3 cm. Find the number of cones so formed.
Answer:
Let the no. of small cones = n Then,
total volume of n cones = Volume of sphere Diameter = 28 cm.
Cones:
Radius r = \(\frac{d}{2}\)

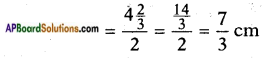
Height, h = 3 cm

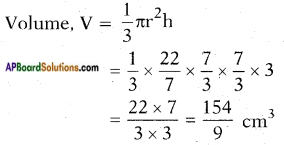
Total volume of n-cones = n . \(\frac{154}{9}\) cm³
Sphere:
Radius = \(\frac{d}{2}\) = \(\frac{28}{2}\) = 14 cm

No. of cones formed = 672.

AP SSC 10th Class Maths Textbook Solutions