Students can go through AP Inter 1st Year Physics Notes 3rd Lesson Motion in a Straight Line will help students in revising the entire concepts quickly.
AP Inter 1st Year Physics Notes 3rd Lesson Motion in a Straight Line
→ Path length is defined as the total length of the path traversed by an object.
→ Displacement is the change in position; ∆x = x2 – x1
→ Average velocity is the displacement divided by the time interval in which the displacement occurs. υ = \(\frac{\mathrm{dx}}{\mathrm{dt}}\)
→ Instantaneous velocity is defined’as the limit of the average velocity as the time interval At becomes infinitesimany small.
![]()
→ Average acceleration is the change in velocity divided by the time interval during which the change occurs, \(\overline{\mathrm{a}}=\frac{\Delta v}{\Delta \mathrm{t}}\)
![]()
→ Instantaneous acceleration is defined as the limit of the average acceleration as the time interval ∆t goes to zero.
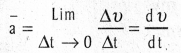
→ Average speed is the ratio of total path length traversed and the corresponding time interval.
→ Equations of motion are
υ = υ0 + at
x = υ0t + \(\frac{1}{2}\) at2
υ2 = υ20 + 2ax
→ Height of a tower is – h = ut – \(\frac{1}{2}\) gt2
→ An object is released near the surface of the earth is accelerated under the influence of gravity. The object is said to be in free fall.
→ Acceleration due to gravity (g) is positive along +y direction and g is negative along – y direction
→ g value in downward motion is negative a = -g = -9.8 m/s2
- v = 0 – gt = -9.8 t
- y = 0 – \(\frac{1}{2}\) gt2 = – 4.9 t2
- υ2 = 0 – 2 gy = -19.6y
![]()
→ Relative velocity is the velocity one body w.r.to velocity of another body.
→ Relative velocity of A w.r.to B = \(\left|\vec{V}_A-\vec{V}_R\right|\)
→ Relative velocity of B w.r.to A = \(\left|\vec{V}_B-\vec{V}_A\right|\)
→ Dimensional formula of velocity = [LT-1].
→ Dimensional formula of acceleration = [LT-2].
