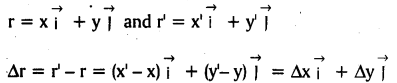Students can go through AP Inter 1st Year Physics Notes 4th Lesson Motion in a Plane will help students in revising the entire concepts quickly.
AP Inter 1st Year Physics Notes 4th Lesson Motion in a Plane
→ A physical quantity having only magnitude but no direction is called a scalar.
→ A physical quantity having magnitude as well as direction and obeys law of addition of vectors is called a vector.
→ A vector of zero magnitude is called null vector for) zero vector.
→ Vectors situated in the same plane are called coplanar vectors.
→ A vector with magnitude one is called unit vector.
→ A vector ‘a1 can be represented in unit vector form as a = axi + ayj + azk. The magnitude of
\(|\vec{a}|=\sqrt{a_x^2+a_y^2+a_z^2}\)
![]()
→ Resultant of any two vectors is determined by parallelogram law of vectors.
R = \(\sqrt{\mathrm{P}^2+\mathrm{Q}^2+2 \mathrm{PQ} \cos \theta}\), tan α = \(\frac{Q \sin \theta}{P+Q \cos \theta}\)
→ Relative velocity is defined as the velocity of one body w.r. to other body.
→ Relative velocity of A w.r. to B = | VA – VB|
→ Relative velocity of B w.r. to A = | VB – VA|
→ Dot product of two vectors is given by \(\vec{a} \cdot \vec{b}\) = ab cos θ
→ Cross product of two vectors \(\vec{p}\) and \(\vec{Q}\) is given by \(\overrightarrow{\mathrm{P}} \times \overrightarrow{\mathrm{Q}}=\mathrm{PQ} \sin \theta \hat{\mathrm{n}}\)
∴ \(|\vec{P} \times \vec{Q}|=\left|\begin{array}{ccc}
i & 1 & k \\
P_x & P_y & P_z \\
Q_x & Q_y & Q_z
\end{array}\right|\)
→ Two vectors A and B are said to be equal if and only if, they have the same magnitude and the same direction.
→ The equation of motion for a projectile is given by y = (tan θ0)x – \(\frac{\mathrm{g}}{2\left(\mathrm{v}_0 \cos \theta_0\right)^2}\) x2 After t seconds (v0) remains the same and final velocity is given by v0 = sin θ – gt
→ The time taken by the projectile to reach the maximum height is given by ta = \(\frac{v_0 \sin \theta}{g}\)
The time of descent is equal to the time of ascent time of flight is given by T = \(\frac{2 v_0 \sin \theta}{g}\)
→ Maximum height reached by the projectile (H) = \(\frac{\left(v_0 \sin \theta_0\right)^2}{2 g}\)
![]()
→ For angles of projection (45° + α) and (45° – α) the range is the same for a given initial velocity.
→ Horizontal range is given by R = \(\frac{v_0^2 \sin 2 \theta_0}{g}\)
→ Maximum Range (Rmax) = \(\frac{v_0^2}{g}\)
→ The velocity of the projectile at any instant t is given by v = \(\sqrt{v_x^2+v_y^2}\) where vx = υ0 cos θ, vy = v0 sin θ – gt
→ The resultant acceleration of an object in circular motion is towards the centre only if the speed is constant.
→ The shape of the trajectory of the motion of an object is not determined by the acceleration alone but also depends on the initial conditions of motion.
→ The position vector of an object in x – y plane is given by