AP Board 10th Class Maths Solutions Chapter 8 సరూప త్రిభుజాలు Exercise 8.2

SCERT AP 10th Class Maths Textbook Solutions Chapter 8 సరూప త్రిభుజాలు Exercise 8.2 Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 8th Lesson సరూప త్రిభుజాలు Exercise 8.2

ప్రశ్న 1.
ఇచ్చిన పటంలో, ∠ADE = ∠B
(i) AABC – AADE అని చూపండి.
(ii) AD = 3.8 సెం.మీ., AE = 3.6 సెం.మీ. BE = 2.1 సెం.మీ. BC = 4.2 సెం.మీ. అయిన DE పొడవును కనుగొనండి.

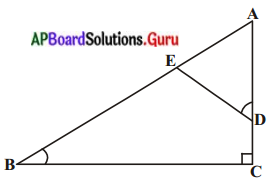
సాధన.
(i) దత్తాంశము : ∆ABCలో ∠ADE = ∠B
సారాంశము : ∆ABC ~ ∆ADE.
ఉపపత్తి : ∆ABC మరియు ∆ADE లలో
∠A = ∠A (∵ ఉమ్మడి కోణము]
∠B = ∠ADE [∵ దత్తాంశము)
∠C = ∠AED ∵ త్రిభుజ కోణాల మొత్తము ధర్మము)
∴ ∆ABC ~ ∆ADE (కో.కో.కో సరూపకత నియమం ప్రకారం)

(ii) దత్తాంశము : AD = 3.8 సెం.మీ., AE = 3.6 సెం.మీ., BE = 2.1 సెం.మీ., BC = 4.2 సెం.మీ.,
సారాంశము : \(\overline{\mathrm{DE}}\) పొడవు.
ఉపపత్తి : ∆ABC ~ ∆ADE కావున \(\frac{\mathrm{AB}}{\mathrm{AD}}=\frac{\mathrm{BC}}{\mathrm{DE}}=\frac{\mathrm{AC}}{\mathrm{AD}}\) [∵ అనురూప భుజాల నిష్పత్తులు సమానము]
ఆ విధముగా \(\frac{4.2}{\mathrm{DE}}=\frac{3.6+2.1}{3.8}\) [∵ AB = AE + BE]
\(\frac{4.2}{\mathrm{DE}}=\frac{5.7}{3.8}\)
DE = \(\frac{4.2 \times 3.8}{5.7}=\frac{42 \times 38}{57 \times 10}\) = 2.8 సెం.మీ.

ప్రశ్న 2.
రెండు సరూప త్రిభుజాల చుట్టుకొలతలు వరుసగా 30 సెం.మీ మరియు 20 సెం.మీ. మొదటి త్రిభుజములోని ఒక భుజము కొలత 12 సెం.మీ, అయిన రెండవ త్రిభుజములో దాని అనురూప భుజము కొలతను కనుగొనండి.
సాధన.

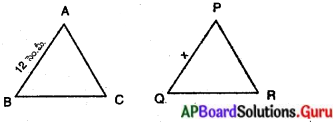
దత్తాంశము : ∆ABC ~ ∆PQR.
∆ABC చుట్టుకొలత = 30 సెం.మీ.
∆PQR చుట్టుకొలత = 20 సెం.మీ.
AB = 12 సెం.మీ.

∴ \(\frac{30}{20}=\frac{12}{x}\)
30 x = 20 × 12
x = \(\frac{20 \times 12}{30}\) = 8 సెం.మీ.

ప్రశ్న 3.
90 సెం.మీ ఎత్తు గల ఒక బాలిక దీపస్తంభము నుండి దూరముగా 1.2మీ/సె. వేగముతో నడుచు చున్నది. దీపస్తంభము ఎత్తు 3.6 మీ అయిన 4 సెకండ్ల తరువాత ఏర్పడే ఆ బాలిక నీడ పొడవును కనుగొనుము.
సాధన.

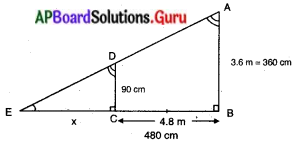
దత్తాంశము : దీపపు స్తంభము ఎత్తు. = 3.6 మీ. = 360 సెం.మీ.
బాలిక వేగము = 1.2 మీ/సె.
4 సెకన్లలో బాలిక ప్రయాణించే దూరము = వేగము × కాలము = 1.2 × 4 = 4.8 మీ. = 480 సెం.మీ.
పటంలో \(\overline{\mathrm{CD}}\), బాలిక ఎత్తు = 90 సెం.మీ.
దీపపు స్తంభము నుండి బాలిక 4.8 మీ. ల దూరంలో ఉన్నపుడు బాలిక నీడ పొడవు = x మీ|| అనుకొనుము.
పటము నుండి ∆ABE ~ ∆DCE
[∵ ∠B = ∠C = 90° ∠E = ∠C ఉమ్మడి భుజం కో.కో సరూపకత ప్రకారం]
\(\frac{\mathrm{AB}}{\mathrm{DC}}=\frac{\mathrm{BE}}{\mathrm{CE}}=\frac{\mathrm{AE}}{\mathrm{DE}}\)

\(\frac{360}{90}=\frac{480+x}{x}\)

⇒ 4 = \(\frac{480+x}{x}\)
⇒ 4x = 480 + x
⇒ 4x – x = 480
⇒ 3x = 480
⇒ x = \(\frac{480}{3}\) = 160 సెం.మీ = 1.6 మీ.
∴ బాలిక నీడ పొడవు = 1.6 మీ.

ప్రశ్న 4.
CM మరియు RN లు వరుసగా ∆ABC మరియు ∆PQR లలో గీయబడిన మధ్యగత రేఖలు. ∆ABC ~ ∆POR అయిన
(i) ∆AMC ~ ∆PNR
(ii) \(\frac{\mathbf{C M}}{\mathbf{R N}}=\frac{\mathbf{A B}}{\mathbf{P Q}}\)
(iii) ∆CMB ~ ∆RNQ అని చూపండి.

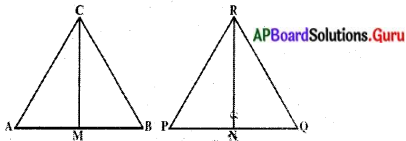
సాధన.
దత్తాంశము : ∆ABC ~ ∆PQR
CM, ∆ABC లో గీయబడిన మధ్యగతరేఖ
RN, ∆PQR లో గీయబడిన మధ్యగతరేఖ
సారాంశము:
(i) ∆AMC ~ ∆PNR.
(ii) \(\frac{\mathrm{CM}}{\mathrm{RN}}=\frac{\mathrm{AB}}{\mathrm{PQ}}\)
(iii) ∆CMB ~ ∆RNQ
ఉపపత్తి :
(i) ∆AMC మరియు ∆PNR లలో
\(\frac{\mathrm{AC}}{\mathrm{PR}}=\frac{\mathrm{AM}}{\mathrm{PN}}\) మరియు ∠A = ∠P
[∵ ∆ABC, ∆PQR లలో \(\frac{\mathrm{AC}}{\mathrm{PR}}=\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\frac{1}{2} \mathrm{AB}}{\frac{1}{2} \mathrm{PQ}}\) మరియు M, N లు AB మరియు PQల మధ్య బిందువులు]
∴ ∆AMC ~ ∆PNR. [∵ భు. కో. భు సరూపకత నియమము నుండి]

(ii) (i) నుండి ∆AMC ~ ∆PNR కావున
\(\frac{\mathrm{AC}}{\mathrm{PR}}=\frac{\mathrm{AM}}{\mathrm{PN}}=\frac{\mathrm{CM}}{\mathrm{RN}}\) [∵ రెండు సరూప త్రిభుజాల అనురూపభుజాల నిష్పత్తి సమానము]
ఆ విధముగా \(\frac{\mathrm{CM}}{\mathrm{RN}}=\frac{\mathrm{AM} \times 2}{\mathrm{PN} \times 2}\) [లవ, హారాలను ‘2’ చే గుణించగా] CM _ AB
\(\frac{\mathrm{CM}}{\mathrm{RN}}=\frac{\mathrm{AB}}{\mathrm{PQ}}\) [2AM = AB; 2PN = PO]

(iii) ∆CMB మరియు ∆RNQ లలో ∠B = ∠Q [∆ABC ~ ∆PQR కావున వాటి అనురూప కోణాలు]
మరియు \(\frac{\mathrm{BC}}{\mathrm{RQ}}=\frac{\mathrm{BM}}{\mathrm{QN}}\)
[∵ \(\frac{\mathrm{BC}}{\mathrm{RQ}}=\frac{\mathrm{AB}}{\mathrm{PQ}} \Rightarrow \frac{\mathrm{BC}}{\mathrm{PQ}}=\frac{\frac{1}{2} \mathrm{AB}}{\frac{1}{2} \mathrm{PQ}}\)]
ఆ విధముగా భు.కో. భు సరూపకత నియమము ప్రకారము
∆CMB ~ ∆RNQ.

ప్రశ్న 5.
ట్రెపీజియం ABCD లో AB || DC. కర్ణములు AC మరియు BD లు బిందువు ‘0’ వద్ద ఖండించుకొనును. త్రిభుజముల సరూప నియమాలను ఉపయోగించుకొని \(\frac{O A}{O C}=\frac{O B}{O D}\) అని చూపండి.
సాధన.

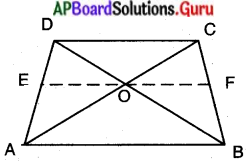
దత్తాంశము : ట్రెపీజియమ్ ABCDలో AB || DC. కర్ణములు AC మరియు BD లు బిందువు ‘0’ వద్ద ఖండించుకొనును. .
సారాంశము : \(\frac{O A}{O C}=\frac{O B}{O D}\)
నిర్మాణము : AB కు సమాంతరంగా ‘0’ గుండా EF ను గీయుము.
ఉపపత్తి : ∆ACD లో, OE || CD [∵ నిర్మాణాల నుండి]
కావున \(\frac{\mathrm{OA}}{\mathrm{OC}}=\frac{\mathrm{EA}}{\mathrm{ED}}\) …………. (1)
(∵ ప్రాథమిక అనుపాత సిద్ధాంతం నుండి)
∆ABD లో OE || AB (నిర్మాణం నుండి)
కావున \(\frac{\mathrm{EA}}{\mathrm{ED}}=\frac{\mathrm{OB}}{\mathrm{OD}}\) ………….. (2) (∵ ప్రాథమిక అనుపాత సిద్ధాంతం నుండి)
(1), (2) ల నుండి \(\frac{O A}{O C}=\frac{O B}{O D}\) అని నిరూపించబడింది.

ప్రశ్న 6.
AB, CD, PQలు BD కి గీసిన లంబాలు. AB = x, CD = Y మరియు PQ = Z అయిన \(\frac{1}{x}+\frac{1}{y}=\frac{1}{z}\) అని చూపండి.
సాధన.
దత్తాంశము : పటం నుండి ∠B = ∠Q = ∠D = 90° మరియు AB || PQ || CD.
∆BQP, ∆BDC లలో
∠B = ∠B (ఉమ్మడి కోణం) , ∠Q = ∠D (90°) ∠P = ∠C (∵ త్రిభుజ కోణాల మొత్తం ధర్మము)
∴ ∆BQP ~ ∆BDC (కో.కో.కో సరూపకత నియమము నుండి)
కావున \(\frac{\mathrm{BQ}}{\mathrm{BD}}=\frac{\mathrm{PQ}}{\mathrm{CD}}\) …………….. (1) [∵ అురూప భుజాల నిష్పత్తులు సమానము)
∆DOP మరియు ∆DBA లలో ∠D = ∠D (ఉమ్మడి కోణము)
∠Q = ∠B . (90)
∴ ∆DQP ~ ∆DBA (కో.కో సరూప సిద్ధాంతం నుండి)
\(\frac{\mathrm{QD}}{\mathrm{BD}}=\frac{\mathrm{PQ}}{\mathrm{AB}}\) ………………..(2)
[∵ అనురూప భుజాల నిష్పత్తులు సమానము]
(1) మరియు (2), లను కూడగా
\(\frac{\mathrm{BQ}}{\mathrm{BD}}+\frac{\mathrm{QD}}{\mathrm{BD}}=\frac{\mathrm{PQ}}{\mathrm{CD}}+\frac{\mathrm{PQ}}{\mathrm{AB}}\)

\(\frac{\mathrm{BQ}+\mathrm{QD}}{\mathrm{BD}}=\mathrm{PQ}\left(\frac{1}{\mathrm{CD}}+\frac{1}{\mathrm{AB}}\right)\) \(\frac{\mathrm{BD}}{\mathrm{BD}}=\mathrm{z}\left[\frac{1}{\mathrm{y}}+\frac{1}{\mathrm{x}}\right]\)

1 = \(z\left(\frac{1}{y}+\frac{1}{x}\right)\)

∴ \(\frac{1}{x}+\frac{1}{y}=\frac{1}{z}\).

ప్రశ్న 7.
4మీ. పొడవు గల ఒక జెండా స్తంభము 6మీ. పొడవు గల నీడను ఏర్పరచును. అదే సమయంలో దగ్గరలో గల ఒక భవనం 24మీ. పొడవు గల నీడను ఏర్పరచిన, ఆ భవనము ఎత్తు ఎంత ?
సాధన.
దత్తాంశము : జెండా స్తంభము పొడవు = 4 మీ.
జెండా స్తంభపు నీడ పొడవు = 6మీ.
భవనపు పొడవు x మీ.|| అయిన దాని నీడ పొడవు 24 మీ.

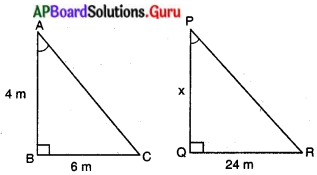
AB = జెండా స్తంభపు పొడవు = 4 మీ.
BC = జెండా స్తంభపు నీడ పొడవు = 6 మీ.
PQ = భవనం ఎత్తు = x మీ. అనుకొనుము.
QR = భవనపు నీడ పొడవు = 24 మీ.
పటం నుండి ∠A = ∠P ∠B = ∠Q
∴ ∆ABC ~ ∆PQR . (కో.కో. సరూపకత నియమము)
కావున \(\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{BC}}{\mathrm{QR}}\)
[∵ అనురూప కోణాల నిష్పత్తి సమానము)
\(\frac{4}{x}=\frac{6}{24}\)
x = \(\frac{24 \times 4}{6}\) = 16 మీ.
∴ భవనం ఎత్తు = 16 మీ.

ప్రశ్న 8.
ABC మరియు FEG త్రిభుజాలలో AB ‘మరియు FE భుజాలపై D మరియు H బిందువులు వరుసగా ఏర్పడునట్లు ∠ACB మరియు ∠EGF లకు గీచిన కోణసమద్విఖండన రేఖలు వరుసగా CD మరియు GH లు ఇంకా ∆ABC ~ ∆FEG అయిన,
(i) \(\frac{\mathbf{C D}}{\mathbf{G H}}=\frac{\mathbf{A C}}{\mathbf{F G}}\)
(ii) ∆DCB ~ ∆HGE
(iii) ∆DCA ~ ∆HGF అని చూపండి.
సాధన.

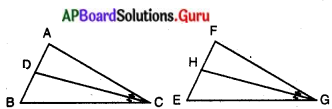
దత్తాంశము : ∆ABC ~ ∆FEG.
CD, ∠ACB యొక్క కోణ సమద్విఖండన రేఖ
GH, ∠EGF యొక్క కోణ సమద్విఖండన రేఖ
సారాంశము :
(i) \(\frac{\mathbf{C D}}{\mathbf{G H}}=\frac{\mathbf{A C}}{\mathbf{F G}}\)
(ii) ∆DCB ~ ∆HGE
(iii) ∆DCA ~ ∆HGF
ఉపపత్తి :
(i) ∆ACD మరియు ∆FGH లలో ∠A = ∠F [∵ ∆ABC ~ ∆FEG లలో అనురూప కోణాలు)
∠ACD = ∠FGH [∵ ∠C = ∠G = \(\frac{1}{2}\)∠C = ∠G ⇒ ∠ACD = ∠FGH]
కో.కో.కో సరూపకత నియమము నుండి ∆ACD ~ ∆FGH
కావున \(\frac{\mathrm{AC}}{\mathrm{FG}}=\frac{\mathrm{CD}}{\mathrm{GH}}=\frac{\mathrm{AD}}{\mathrm{FH}}\) [∵ అనురూప కోణాల నిష్పత్తి సమానము] .
∴ \(\frac{\mathrm{AC}}{\mathrm{FG}}=\frac{\mathrm{CD}}{\mathrm{GH}}\)

(ii) ∆DCB మరియు ∆HGE లలో ∠B = ∠E
[∵ ∆ABC ~ ∆FEG కావున అనురూప కోణాలు సమానము]
∠DCB = ∠HGE
[∵ ∠C = ∠G ⇒ \(\frac{1}{2}\) ∠C = \(\frac{1}{2}\) ∠G ⇒ ∠DCB = ∠HGE]
∴ ∆DCB ~ ∆HGE (కో.కో.కో సరూపకత నుండి)

(iii) ∆DCA మరియు ∆HGF లలో ∠A = ∠F
\(\frac{1}{2}\) ∠C = \(\frac{1}{2}\) ∠G ⇒ ∠DCA = ∠HGF
[∵ సరూప త్రిభుజాల అనురూపక కోణాలు సమానము]
∴ ∆DCA ~ ∆HGF [∵ కో.కో.కో సరూపకత నుండి]

ప్రశ్న 9.
∆ABC మరియు ∆DEF సరూపత్రిభుజాలలో గీసిన లంబాలు AX మరియు DYలు అయిన AX: DY = AB :: DE అని నిరూపించండి.
సాధన.

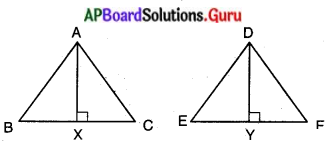
దత్తాంశము : ∆ABC ~ ∆DEF, AX ⊥ BC మరియు DY ⊥ EF.
సారాంశము : AX : DY = AB : DE.
ఉపపత్తి : ∆ABX మరియు ∆DEY లలో ∠ B = ∠ E [∵ ∆ABC ~ ∆DEF లలో అనురూప కోణాలు]
∠ AXB = ∠ DYE = 90°
∴ ∆ABX ~ ∆DEY (కో.కో. కో. సరూపకత నియమము).
⇒ AX : DY = AB : DE [Q.E.D.]
[∵ సరూప త్రిభుజాల యొక్క అనురూప భుజాల నిష్పత్తి]

ప్రశ్న 10.
ఇచ్చిన త్రిభుజము ABCకి సరూపంగా ఉంటూ, దాని భుజాలకు \(\frac{5}{3}\) రెట్లు ఉండే అనురూప భుజాలు కలిగిన త్రిభుజాన్ని నిర్మించండి.
సాధన.

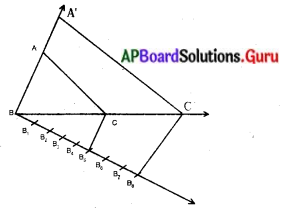
నిర్మాణ సోపానాలు :
(1) ఏవైనా కొలతలతో ∆ABC ను నిర్మించుము.
(2) BC భుజానికి శీర్షము A ఉన్న వైపునకు వ్యతిరేక దిశలో దానితో అల్పకోణము చేయునట్లు BX కిరణమును గీయుము.
(3) ఈ BX పై BB₁ = B₁ B₂ = B₃B₄ = …. అగునట్లు ‘8’ బిందువులు B₁, B₂, B₃, …. B₈. లను గుర్తించుము.
(4) B₅, C ని కలుపుము.
(5) B₅C కి సమాంతరంగా ఉండేటట్లు B₈ వద్ద రేఖను గీయగా అది BC ను C’ వద్ద ఖండించును.
(6) ‘C’ గుండా CA కు సమాంతరంగా గీసిన రేఖ BA ను A’ వద్ద ఖండించును.
(7) ∆A’B’C’ మనకు కావలసిన త్రిభుజము.

ప్రశ్న 11.
4 సెం.మీ, 5 సెం.మీ, 6 సెం.మీ. కొలతలతో ఒక త్రిభుజాన్ని నిర్మించండి. దీనితో సరూపంగా ఉంటూ ఈ త్రిభుజ భుజాలకు రెట్లు అనురూప భుజాల కొలతలు కలిగిన త్రిభుజాన్ని నిర్మించండి.
సాధన.

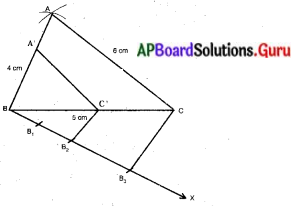
నిర్మాణ సోపానాలు :
(1) AB = 4 సెం.మీ., BC = 5 సెం.మీ మరియు CA = 6 సెం.మీ.ల కొలతలతో ∆ABC ను నిర్మించుము.
(2) BC భుజానికి శీర్షం ‘A’ ఉన్న వైపునకు వ్యతిరేక దిశలో దానితో అల్పకోణము చేయునట్లు BX కిరణమును గీయుము.
(3) ఈ BX పై BB₁ = B₁B₂ = B₂B₃ అగునట్లు మూడు బిందువులు B₁, B₂, B₃ లను గుర్తించుము.
(4) B₃, C లను కలుపుము.
(5) B₂ గుండా B₃ C కి సమాంతరంగా ఉండేటట్లు రేఖను గీసిన అది BC ని C’ వద్ద ఖండించును.
(6) A’ గుండా CA కు సమాంతరంగా గీసిన రేఖ BAను A’ వద్ద ఖండించును.
(7) కావున ∆A’B’C’ మనకు కావలసిన త్రిభుజము.

ప్రశ్న 12.
భూమి 8 సెం.మీ మరియు దానికి గీసిన లంబము 4సెం.మీ. ఉండునట్లు ఒక సమద్విబాహు త్రిభుజమును గీయండి. ఈ ‘త్రిభుజ భుజాలకు 13 రెట్లు అనురూప భుజాల పొడవులు కలిగి, ఇచ్చిన త్రిభుజానికి సరూపంగా ఉండేటట్లు వేరొక త్రిభుజాన్ని నిర్మించండి.
సాధన.
నిర్మాణ సోపానాలు :
(1) BC = 8 సెం.మీ మరియు లంబము 4 సెం.మీ ఉండునట్లు ఒక సమద్విబాహు త్రిభుజమును నిర్మించుము.

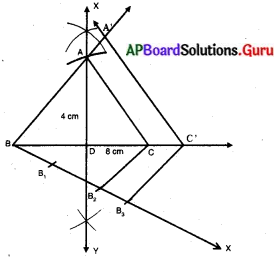
(2) BC భుజానికి శీర్షము A ఉన్న వైపునకు వ్యతిరేక దిశలో దానితో అల్పకోణము చేయునట్లు BX కిరణమును గీయుము.
(3) ఈ BX పై BB₁ = B₁ B₂ = B₂ B₃ అగునట్లు మూడు బిందువులు B₁, B₂, B₃, లను గుర్తించుము.
(4) B₂ C ని కలుపుము. B₂ నుండి B₃ C కి సమాంతరంగా ఉండేటట్లు రేఖను గీసిన అది BC ని C’ వద్ద ఖండించును.
(5) C’ గుండా CA కు సమాంతరంగా గీసిన రేఖ BA ను A’ వద్ద ఖండించును.
(6) కావున ∆A’BC’ మనకు కావలసిన త్రిభుజము.