These AP 9th Class Maths Important Questions 9th Lesson Statistics will help students prepare well for the exams.
AP State Syllabus 9th Class Maths 9th Lesson Important Questions and Answers Statistics
Question 1.
Convert inclusive classes into exclusive classes of the following classes : 10 – 19, 20 – 29, 30 – 39, 40 – 49
Solution:
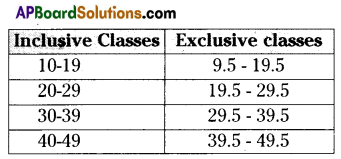
Question 2.
If the mean of 20, 24, 36, 26, 34 and K is 30, then And K.
Solution:
Mean = \(\frac{\text { Sum of items }}{\text { No. of items }}\)
30 = \(\frac{20+24+36+26+34+\mathrm{K}}{6}\)
⇒ 180 = 140 + K
⇒ K = 40
![]()
Question 3.
Find the range of first five prime numbers.
Solution:
First five prime numbers 2, 3, 5, 7, 11.
Maximum number = 11
Minimum number = 2
Range = 11 – 2 = 9
Question 4.
The mean of first ‘n’ natural numbers is x. What is the mean of first ‘n’ even natural numbers.
Solution:
Mean of first ‘n’ even numbers = 2x
Question 5.
In the given formula \(\overline{\mathbf{x}}=\frac{\sum \mathbf{x}_{\mathbf{i}}}{\mathbf{n}}\) what does n, \(\overline{\mathbf{x}}\) denote
Solution:
n = No. of observations
\(\overline{\mathbf{x}}\) = Mean
Question 6.
Find the Median and Mode to the given data.
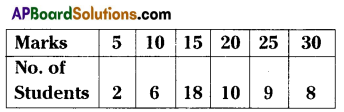
Solution:
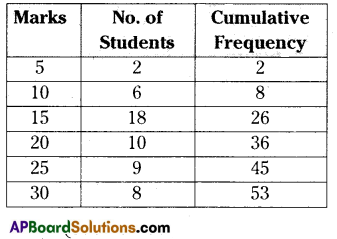
N = 53 (odd number)
\(\frac{\mathrm{N}+1}{2}=\frac{53+1}{2}=\frac{54}{2}\) = 27
∴ Median = 20
∴ Mode = 15
Question 7.
For an ungrouped data 10, 15, 20, 25, 15, x median and mode are equal. Find x and also mean for the above data.
Solution:
Given data = 10, 15, 20, 25, 15, x
When data is arranging in ascending order = 10, 15, 15, x, 20, 25
Mode = x = 15
Median also x = 15
∴ x = 15
Sum of observations
= 10 + 3 x 15 + 20 + 25 = 100
Mean = \(\overline{\mathbf{x}}\) = \(\frac{\Sigma x_{i}}{n}=\frac{100}{6}\) = 16\(\frac{2}{3}\)
![]()
Question 8.
Weights of 40 students in a class are given in the table.

Find the average weight of 40 students.
Solution:

Mean = \(\frac{\Sigma \mathrm{fx}}{\Sigma \mathrm{f}}=\frac{1460}{40}\) = 36.5 kgs.
Question 9.
While finding arithmetic mean for 50 scores of an ungrouped frequency distribution it was given that Σ fi.xi = 755. Find the mean of the scores.
Solution:
Number of observations = 50
Sum of observations = Σfixi = 755
Mean = \(\frac{\Sigma \mathrm{f}_{i} \mathrm{x}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}=\frac{755}{50}\) = 15.1
Question 10.
Median of an ungrouped data 13, 10, 12, 18, 17, p is observed as 14. Find p by giving reasons.
Solution:
Arrange the observations in ascending order = 10, 12, 13, p, 17, 18.
n = 6 (even number)
Mean of \(\frac{n}{2}, \frac{n}{2}\) + 1 is median.
3rd and 4th observations = \(\frac{13+\mathrm{p}}{2}\)= 14
13 + p = 28
p = 28 – 13
p = 12
∴ ‘p’ value is 12.
Question 11.
Find the median of the data.

Solution:

N = 29 (odd number)
So, (\(\frac{n+1}{2}\))th term is median.
∴ Median = 15
Question 12.
If the mean of the following data is 7.5, then find the value of A.

Solution:
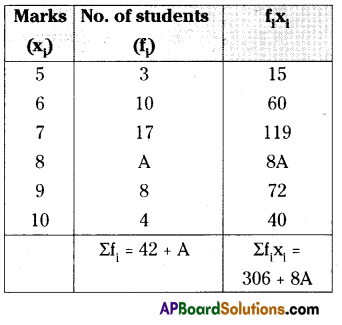
Mean = \(\overline{\mathrm{x}}=\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\sum \mathrm{f}_{\mathrm{i}}}\)
7.5 = \(\frac{306+8 \mathrm{~A}}{42+\mathrm{A}}\)
⇒ 7.5 (42 + A) = 306 + 8A
⇒ 7.5 × 42 + 7.5 A = 306 + 8A
⇒ 315 + 7.5A = 306 + 8A
⇒ 0.5 A = 9
⇒ A = \(\frac{9}{0.5}\)
A = 18
![]()
Question 13.
Find the median marks of the data.

Solution:

Median = (\(\frac{n+1}{2}\))th term as N = 29 is odd
\(\frac{29+1}{2}\) = 15th term
15th observation is 15. (from the table)
Question 14.
Centuries scored and some cricketers in the world are given below.

Find the Mean by using deviation method.
Solution:
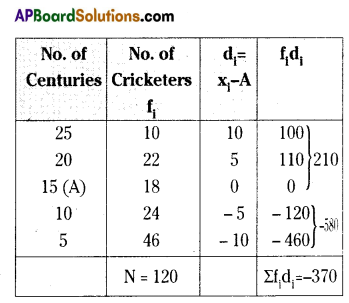
Mean = \(\overline{\mathbf{x}}\) = A + \(\frac{\Sigma \mathrm{f}_{i} \mathrm{~d}_{\mathrm{i}}}{\Sigma \mathrm{f}_{1}}\)
= 15 + \(\frac{(-370)}{120}\)
= 15 – \(\frac{37}{12}\)
= 15 – 3.083 = 11.917
Question 15.
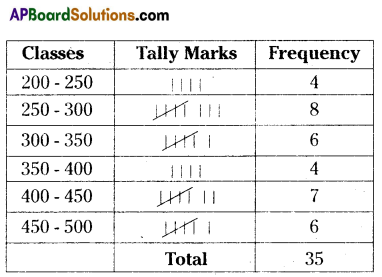
An excellent programme organised by the Central Govt. “SWATCHA BHARAT”. The data of toilets from 35 villages as shown below.

Construct a frequency distribution table with a class size of 50.
Solution:
Maximum value = 475
Minimum value = 209
Range = Maximum value – Minimum value = 266
Class interval = 50
No. of classes = \(\frac{266}{50}\) = 5.32 ≈6
Question 16.
Weights of parcels in a transport office are given below. If the mean weight of the frequency distribution is 85kg, find the value of ‘x’ and also median for the data.

Solution:
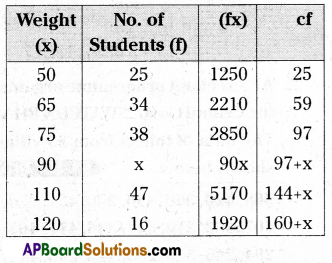
Given that mean = 85
Mean = \(\frac{\Sigma \mathrm{f} \mathrm{x}}{\Sigma \mathrm{f}}\) = \(\frac{13400+90 x}{160+x}\) = 85
13,400 + 90x = 13,600 + 85x
90x – 85x = 13,600-13,400
5x = 200 ⇒ x = 40
Median = N = 160 + 40
= 200 (even number)
= (\(\frac{\mathrm{N}}{2}\) + 1)th = 101thnumber
∴ Frequency of 101 item is = 90
Median = 90
![]()
Question 17.
If the Mean of the following data is 20.6, find the missing frequency ‘P’.

Solution:
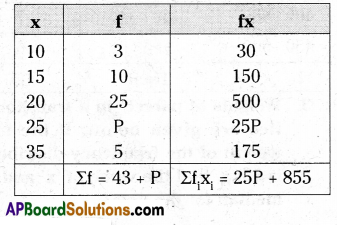
Σfixi = 25P + 855
Σfi = 43 + p
Mean = \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\)
20.6 = \(\frac{855+25 P}{43+P}\)
⇒ 885.8 + 20.6P = 855 + 25P
⇒ 4.4P = 30.8 ⇒ P = 7
Question 18.
Prepare an ungrouped frequency distribution for the following grades obtained by 30 students in SSC public examination using tally marks.

Solution:

Question 19.
The following table gives information on the number of centuries scored by women cricketers in the world.

Find the mean centueries scored
Solution:
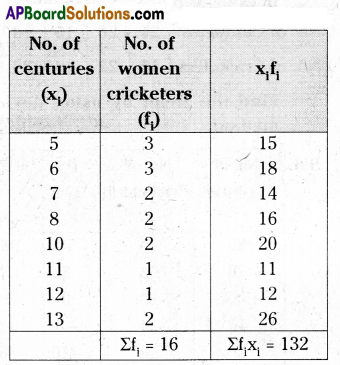
Mean = \(\frac{\Sigma \mathrm{f}_{i} \mathrm{x}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}=\frac{132}{16}\) = 8.25
Question 20.
Find the median and mode of the following data.
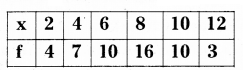
Solution:

N = 50 even;
Median = average of ( \(\frac{\mathrm{N}}{2}\) + 1 and \(\frac{\mathrm{N}}{2}\))th term = average of 25 and 26 observations = 6
Median = 6; Mode = 8
Question 21.
Test scores out of 100 for a class of 20 students are as follows :
93, 84, 97, 98, 100, 78, 86, 100, 85, 92, 55, 91, 90, 75, 94, 83, 60, 81, 95, 77.
i) Make a frequency table taking class intervals as 51 – 60, 61 – 70,……………..
ii) Find the modal class.
iii) Find the median class.
Solution:
i) Test scores of 20 students for 100 marks are given below
93, 84, 97, 98, 100, 78, 86,100, 85, 92, 55, 91, 90, 75, 94, 83, 60, 81, 95, 77
Range = Maximum value – Minimum value
= 100 – 55 = 45
Length of the class / class interval = 10 [∵ 51 – 60,61 -70]
No. of classes
\(\frac{\text { Range }}{\text { length of the class }}\) = \(\frac{45}{10}\) = 4.5 ~ 5

\(\frac{N}{2}=\frac{20}{2}\) = 10
ii) Modal class : 91 – 100
[ ∵ maximum frequency is 10, which corresponds to the C.l → 91 – 100]
iii) Median class : 81 – 90
[∵ \(\frac{\mathrm{N}}{2}\) occurs at the cumulative frequency 10, which corresponds to the C.I 81 – 90]
![]()
Question 22.
A trust initiated savings programme among the high school children in Krishna District. Mandal wise amount saved in a month are shown in the following table. Find the arithmetic mean of savings of ALL schools.
Solution:
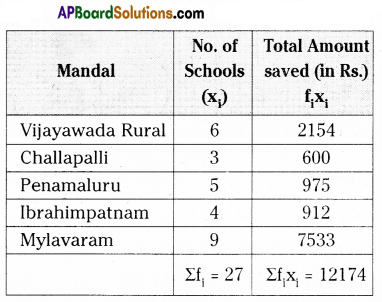
∴ A.M = \(\overline{\mathrm{x}}=\frac{\sum \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\sum \mathrm{f}_{\mathrm{i}}}=\frac{12174}{27}\) = 450.88
∴ The arithmetic mean of savings of all schools = ₹ 451/-
