These AP 9th Class Maths Important Questions 8th Lesson Quadrilaterals will help students prepare well for the exams.
AP State Syllabus 9th Class Maths 8th Lesson Important Questions and Answers Quadrilaterals
Question 1.
The four angles of quadrilateral are in the ratio 2 : 4 : 5 : 7. Find it’s angles.
Solution:
Ratio of angles of quadrilateral = 2 : 4 : 5 : 7
Let the four angles be 2x, 4x, 5x and 7x.
Sum of them = 2x + 4x + 5x + 7x = 360°
⇒ 18x = 360° ⇒ x = 20°
∴ Angles in a quadrilateral = 40°, 80°, 100°, 140°
Question 2.
Draw a diagram representing the following data.
“In a triangle ABC, AD is the median drawn on to the side BC is produced to E such that AD = ED to form a ABEC parallelogram”.
Solution:
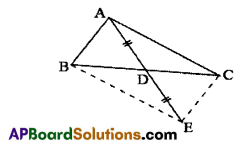
![]()
Question 3.
The ratio of consecutive angles of a parallelogram is 2 : 3. Find the angles.
Solution:
Ratio of angles = 2 : 3
Let the angles are 2x and 3x.
Sum of adjacent angles in a parallelogram is 180°.
∴ 2x + 3x = 180°
5x = 180° ⇒ x° = 36°
∴ Angles are = 2x = 2 × 36° = 72°
= 3x = 3 × 36° = 108°
Question 4.
D, E and F are midpoints of the sides of triangle ABC respectively, if AB = 8 cm., BC 7.2 cm, and AC = 6 cm. then find the perimeter of ΔDEF.
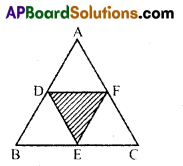
Solution:
DF = BC = × 7.2 = 3.6 cm
DE = \(\frac{1}{2}\) AC = \(\frac{1}{2}\) × 6 = 3cm
EF = \(\frac{1}{2}\) AB = \(\frac{1}{2}\) × 8 = 4 cm
∴ Permiter of ΔDEF = 3.6 + 3 + 4 = 10.6 cm
Question 5.
ABCD is a parallelogram and ∠D = 150°. The side AB is produced to E. Then find the measure of ∠CBE.
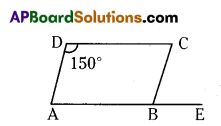
Solution:
From figure ∠B = ∠D {ABCD is a parallelogram}
∠B = 150°
∠CBA + ∠CBE = 180° {Linear pair} 150° + ∠CBE = 180°
∠CBE = 180° – 150° = 30°
Question 6.
ABCD is a rhombus and ∠A = 60°, find the measure of ∠C and ∠B.
Solution:
ABCD is a rhombus in which ∠A = 60° then ZC = 60° [ ∵ ∠A, ∠C are the opposite angles, which are equal in a rhombus]
∠A + ∠B = 180° [Sum of adjacent angles of a rhombus are supplementary]
60° + ∠B = 180°
∴ ∠B = 180° – 60° = 120°
![]()
Question 7.
Write whether the following statements are true (or) false. Justify your answer.
i) A rhombus is a parallelogram,
ii) For any real number x, x2 ≥ 0.
iii) The sum of the interior angles of a quadrilateral is 350°.
iv) Square numbers can be written as the sum of two odd numbers.
Solution:
i) A Rhombus is a parallelogram. This statement is true. Because squares, – rectangles and rhombuses are all parallelograms.
ii) For any real number x, x2 ≥ 0. This statement is true. Because square of a real number cannot be negative and it can be equal or greater than zero.
iii) The sum of the interior angles of a quadrilateral is 350°. This statement is false. Because of the sum of the interior angles of a quadrilateral is 360°.
iv) Square numbers can be written as the sum of two odd numbers. This statement is true. Square number will always be even. The sum of two odd numbers is always an even number.
Question 8.
In the given figure CD || BE || AF. Prove that ar(ΔAEC) = ar (ΔDBF).
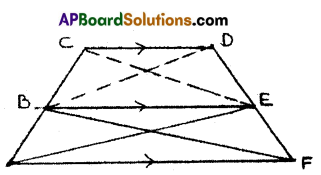
Solution:
Area of triangles between same base and same parallel lines are equal.
∴ ΔCBE area = ΔDBE area
ΔBAE area = ΔBEF area
ΔCBE + ΔBAE = ΔDBE + ΔBEF
∴ Area of ΔAEC = area of ΔDBF
Question 9.
The angles of a quadrilateral are in the ratio 1 : 2 : 3 : 3. Find the measure of each angle of the quadrilateral.
Solution:
Ratio of angles = 1 : 2 : 3 : 3
Angles of quadrilateral x, 2x, 3x and 3x.
x + 2x + 3x + 3x = 360°
9x = 360°
x = \(\frac{360}{9}\) = 40°
First angle = x = 40°
Second angle = 2x = 80°
Third angle = 3x = 120°
Fourth angle = 3x = 120°
Question 10.
The opposite angles of a parallelogram are (3x – 2)° and (x + 48)°. Find the measure of each angle of the parallelogram.
Solution:
Opposite angles of a parallelogram are given.
They are (3x – 2)°, (x + 48)°
⇒ 3x – 2 = x + 48° [ ∵ opposite angles of a parallelogram are equal]
⇒ 3x – x = 48 + 2 => 2x = 50
∴ x = 25°

A = 3x – 2° = 3 x 25° -2° = 75° -2° = 73°
∠A = ∠C = 73°
∠B = 180° – ∠A [ v adjacent angles of a parallelogram are supplementary]
= 180° – 73° = 107°
∴ ∠B = ∠D = 107°
![]()
Question 11.
i) ABCD is a quadrilateral such that AB = BD, AC = CD. Show that ΔABC ≅ ΔDBC.
ii) ABCD is a quadrilateral such that AD = BC and ∠DAB = ∠CBA.
Show that ΔABD ≅ ΔBAC.
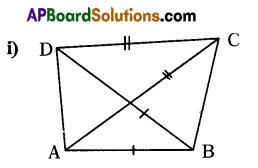
ABCD is a quadrilateral in which
AB = BD
AC = CD
from ΔABC & ΔDBC
AB = DB (S) (given)
AC = DC (S) given
BC = BC (S) (common side)
By side – side – side congruency rule ΔABC ≅ ΔDBC
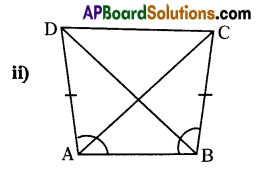
Proof : ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA from A ABD & Δ BAC
AD = BC (S) (given)
∠DAB = ∠CBA (A) given
AB = AB (S) (common side)
∴ By S.A.S congruency rule ΔABD ≅ ΔBAC
