AP 9th Class Maths Important Questions Chapter 7 Triangles

These AP 9th Class Maths Important Questions 7th Lesson Triangles will help students prepare well for the exams.

AP State Syllabus 9th Class Maths 7th Lesson Important Questions and Answers Triangles

Question 1.
The interior angles of a triangle are (3x – 10)°, (3x + 10)°, (3x)°. Find the angles.
Solution:
Interior angles of a triangle are (3x- 10)°, (3x + 10)° and (3x)°
Sum of angles = (3x – 10)° + (3x + 10)° + (3x)° = 180°
9x = 180°
x = 20°
∴ Angles = 3 × 20 – 10 = 60 – 10 = 50°
= 3 × 20 + 10 = 60 + 10 = 70°
= 3 × 20° ± 60°
∴ Angles are 50°, 70° and 60°.

Question 2.
If ΔABC ≅ ΔPQR, express equal sides of triangles.
Solution:
If Δ ABC ≅ ΔPQR
⇒ AB = PQ, BC = QR, AC = PR

Question 3.
In ΔABC, the lines are drawn parallel to BC, CA and AB respectively through A, B, C intersecting at P, Q and R. Find the ratio of perimeter of ΔPQR and ΔABC
Solution:

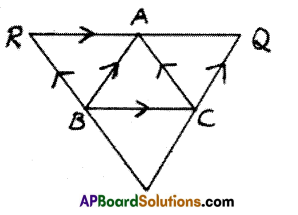
From figure, AB // QP and BC // RQ.
So, in ABCQ parallelogram AB // CQ
Similarly, in BCAR, ABPC parallelograms BC = AQ and BC = RA.
Mid point of QR is ‘A’.
Similarly mid point of PR and PQ is B and C.
∴ AB = \(\frac{1}{2}\) PQ,
BC = \(\frac{1}{2}\) QR and CA = \(\frac{1}{2}\) PR.
∴ Perimeter of ΔPQR = PQ + QR + PR
= 2AB + 2BC + 2CA
= 2 (AB + BC + CA)
= 2(Perimeter of ΔABC)
∴ Ratio of perimeters of ΔPQR and ΔABC is 2 : 1.

Question 4.
In the adjacent figure, prove that ΔPQX ≅ ΔPRY.

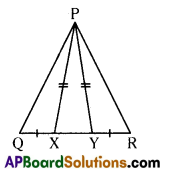
Solution:
In ΔPQX, ΔPRY .
Sides QX = RY {Given}
Sides PX = PY {Given}
∠PXY = ∠PYX
180 – ∠PXY = 180° – ∠PYX
⇒ ∠PXQ = ∠PYR {Angle}
By S – A – S congruence criterion.
ΔPQX ≅ ΔPRY

Question 5.
In the given figure, AL is parallel to DC and E Is mid point of BC. Show that triangle EBL Is congruent to triangle ECD.

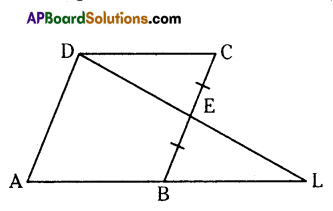
Solution:
From the adjacent figure AL // CD and E is the midpoint of BC.
i.e., BE = EC
from ΔBEL & ΔCED.
∠B = ∠C [ ∵ Alternate interior angles]
∠DEC = ∠BEL [ ∵ vertically opposite, angles]
∴ By A.S.A rule
Δ EBL ≅ Δ ECD.

Question 6.
ABC is a right angled triangle and M is the midpoint of the hypotenuse AB. A line segment MD, parallel to BC, passes through M and meets AC at D. Prove that (i) D is midpoint of AC, (ii) MD is perpendicular to AC.

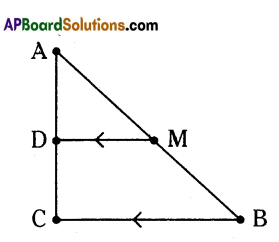
Solution:
Given that ΔABC is a right angled triangle in which, M is the midpoint of AB. Also \(\overline{\mathrm{MD}}\) / / \(\overline{\mathrm{BC}}\).
∠C = 90° ⇒ BC⊥AC then MD JL AC [ ∵ BC // MD]
If a line is drawn parallel to one side and (divides the 2^nd side into two equal parts) passes through the midpoint of second side, it will also passes through the midpoint of 3^rd side, i.e., MD bisects AC.
i.e., D is the midpoint of AC.

Question 7.
In ΔPQR, PS⊥QR and ΔPQS ≅ ΔPRS.

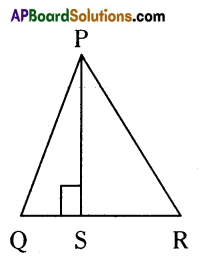
PQ = 2x + 3, PR = 3y + 1, QS = x,
SR = y + 1. Find the area of ΔPQR.
Solution:

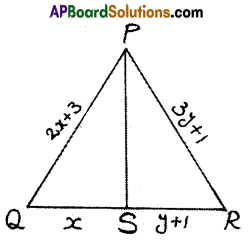
In ΔPQR, PS⊥QR, so ΔPRS ≅ ΔPQS From CPCT,
PQ = PR and QS = SR and 2x + 3 = 3y + 1 and x = y + 1
2x – 3y = -2 ………………… (1) and
x – y = 1 ………….. (2)
Substitute x = y + 1 in equation (1)
2(y + 1) – 3y = -2
2y + 2 – 3y = -2
-y = -4
⇒ y = 4
by y = 4 in x = y+ 1 ⇒ x = 5
∴ QR = x + y+ l= 5 + 4+ l = 10units
PQ = PR = 2(5) + 3 = 13 units
QS = x = 5 units.
∴ ΔPQS is a right triangle.
From pythagoras theorem,
PQ² = QS² + PS²
PS² = PQ² – QS²
PS² = (13)³ – (5)² = 144
∴ PS = 12 units
∴ Area of ΔPQR = \(\frac{1}{2}\) × QR × PS
= \(\frac{1}{2}\) × 10 × 12 = 60,sq.units.

Question 8.
In the given figure \(\overline{\mathrm{AB}}\) || \(\overline{\mathrm{CD}}\) || \(\overline{\mathrm{EF}}\) at equal distances and AF is a transversal. \(\overline{\mathrm{GH}}\) is perpendicular to \(\overline{\mathrm{AB}}\). If AB = 4.5 cm, GH = 4 cm and FB = 8 cm, find the area of ΔGDF.

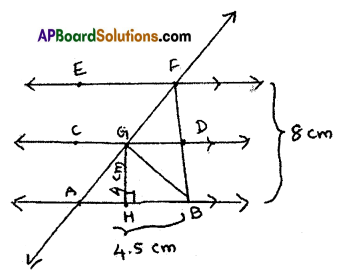
Solution:
In the given figure \(\overline{\mathrm{AB}}\) || \(\overline{\mathrm{CD}}\) || \(\overline{\mathrm{EF}}\) at equal distances.
\(\overline{\mathrm{AF}}\) is a transversal and \(\overline{\mathrm{GH}}\) is perpendicular to \(\overline{\mathrm{AB}}\).
So, GH = 4 cm, AB = 4.5 cm, FB = 8 cm To find area of ΔGDF,
From ΔABF, D is mid point of \(\overline{\mathrm{BF}}\)
Similarly ‘G’ is mid point of \(\overline{\mathrm{AF}}\).
So BD ⊥ DF, AG = GF
Median divides a triangle into two equal triangles.
∴ Area of ΔABG = Area of ΔBGF
Similarly \(\overline{\mathrm{GD}}\) is median of ΔBGF.
Area of ΔABG = 2 × area of ΔDGF
Area of ΔDFG = \(\frac{1}{2}\) area of ΔABG
Area of ΔABG = \(\frac{1}{2}\) × 4.5 × 4 = 9 sq.cm
Area of ΔDGE = \(\frac{1}{2}\) × 9 = 4.5 sq.cm

Question 9.
In ABC, E and F are mid points of sides AB and AC respectively then prove that i) EF // BC and ii) EF = \(\frac{1}{2}\)BC.
Solution:
Given : B and F are mid points of AB and AC.

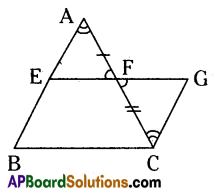
R.T.P. : i) EF // BC, ii) EF = \(\frac{1}{2}\) BC
Construction: ..
GC // AB, extend EF upto G.
Proof:
ΔAEF ACGF
∠AFE = ∠CFG (Vertically opposite angles)
AF = FC
∠EAF = ∠GCF (Alternate angles)
∴ ΔAEF = ΔCGF
∴ CG = BE and CG // BF (Construction)
∴ EBCG is a parallelogram.

Question 10.
In triangle ABC, D is a point on BC such that ΔABD and ΔACD are congruent. Find the values of x and y, if AB = 2x + 3, AC = 3y + 1, BD = x and
DC = y + 1.
Solution:
From the adjacent figure ΔABC, D is a point on BC.

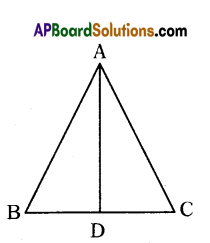
Such that ΔABD ≅ ΔACD

AB = 2x + 3
AC = 3y + 1

BD = x
DC = Y + 1

Δ ABD = Δ ACD
⇒ AB = AC
⇒ 2x + 3 = 3y + 1
⇒ 2x – 3y + 2 = 0 …………….(1)
BD = CD ⇒ x = y + 1
⇒ x – y – 1 = 0 ………………….(2)
⇒ from (1) & (2)

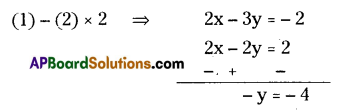
y = 4
from (2) ⇒ x – 4 = 1
⇒ x = 1 + 4 = 5
∴ (x, y) = (5, 4)

Question 11.
In triangle ΔABC, D, E and F are mid points of sides AB’, BC and AC respectively. If we join points D, E and F, then show that triangle ABC is divided into four congruent triangles.

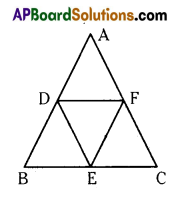
Solution:
Given : In ABC, D,E,F are the midpoints of sides AB, BC and AC respectively. .
R.T.P : ΔADF ≅ ΔDBE ≅ ΔDEF ≅ ΔCEF
Proof : D, E are the midpoints of \(\overline{\mathrm{AB}}\) and \(\overline{\mathrm{BC}}\) of ΔABC respectively.
So by mid-point theorem, we know that DE // AC
Similarly DF//BC and EF // AB.
∴ ADEF, BEFD, CFDE are all parallelograms.
In a parallelogram ADEF, DF is the diagonal.
So, ΔADF ≅ ΔDEF …………….. (1)
[∵ Diagonal divides the parallelogram into two congruent triangles]
Similarly ΔBDE ≅ ΔDEF ………………… (2)
and ΔCEF ≅ ΔDEF …………….. (3)
From (1), (2) & (3) ⇒ ΔADF ≅ ΔDEF ≅ ΔBDE ≅ ΔCEF all the triangles are congruent to each other,
i.e., ΔABC divides into four congruent triangles by joining the mid points of the sides.